排序算法群星豪华大汇演

DSQiu

浏览: 1397485 次
性别:
来自: 广州

最近访客更多访客>>

ymgjava

spike_wq

sdsunrunner

hackxboy

博主相关

博客

微博

相册

留言

关于我

博客专栏

: NGUI所见即所得
浏览量：195162

: Effective C# ...
浏览量：0

文章分类

社区版块

存档分类

博客分类：

排序算法群星豪华大汇演

排序算法相对简单些，但是由于它的家族比较庞大——这也许是因为简单的缘故吧，网上整理排序算法实在太多了，什么经典排序算法，八大排序算法总结，精通八大排序算法等枚不胜举，当然这里也不例外，同样是整理，同样是学习的过程。

之前一些排序算法总是说不清楚（作者自己的感受），这倒不是因为太难，作者觉得是因为排序算法太繁复了（一些算法之间的区别不是很明显），那也没有他法，只有各个击破，认真理解每个排序的原理。经过一段时间的学习和整理，已经剧本一定的规模，故作一个总览，方便查阅。

交换排序（exchange sorts）算法大串讲

§1 冒泡（Bubble Sort）排序及其改进

§2 鸡尾酒（Cocktail Sort）排序

§3 奇偶（Odd-even Sort）排序

§4 快速（Quick Sort）排序及其改进

§5 梳（Comb Sort）排序

§6 地精(Gnome Sort）排序

选择排序（selection sorts）算法大串讲

§1 选择排序

§2 锦标赛排序

§3 堆排序

§4 Smooth Sort

插入排序（insertion sorts）算法大串讲

§1 基本插入排序算法和折半插入排序算法

§2 希尔排序（shell sort）算法

§3 图书馆排序（library sort）算法

§4 耐心排序（patience sort）算法

归并排序（merge sorts）算法大串讲

§1 归并排序（Merge Sort）

§2 归并排序算法改进和优化

§3 Strand Sort排序

分布排序（distribution sorts）算法大串讲

§1 鸽巢排序（Pigeonhole）

§2 桶排序（Bucket Sort）

§3 基数排序（Radix Sort）

§4 计数排序（Counting Sort）

§5 Proxmap Sort

§6 珠排序(Bead Sort）

当然，对于浩大的排序算法，这里只能列举部分，对其进行分别介绍，有的介绍相对简单，有的比较反复，日后有时间学习再详加论述，可能有些读者会觉得每个算法讲解时间复杂度（其实都尽力覆盖）和应用会相对少点（作者也是一直这么期待多点应用），但是作者觉得这些都是建立在对算法原理的充分理解的基础上的，换句话说，如果能充分理解算法的真谛，时间复杂度和空间复杂度那其实不是信手拈来的事吗，至于应用主要是要结合实际问题，就想人生的阅历一样只有在漫长时间的浸泡才会逐渐丰满起来，所以学习切勿本末倒置，孰能生巧（掌握基本的排序算法，混合排序算法（作者没有进行整理，作者认为只要充分掌握基本的原理，遇到实际问题自然就会想到的）就不在话下了才是学习真正在的过程，学习是要学习融会贯通的能力，当然这也需要积累的过程。

下面再附上维基百科的对Sort Algorithm的整理：

Comparison of algorithms

In this table, n is the number of records to be sorted. The columns "Average" and "Worst" give the time complexity in each case, under the assumption that the length of each key is constant, and that therefore all comparisons, swaps, and other needed operations can proceed in constant time. "Memory" denotes the amount of auxiliary storage needed beyond that used by the list itself, under the same assumption. These are all comparison sorts. The run time and the memory of algorithms could be measured using various notations like theta, omega, Big-O, small-o, etc. The memory and the run times below are applicable for all the 5 notations.

Comparison sorts Name Best Average Worst
Memory Stable Method
Other notes

Quicksort	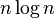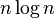$\mathcal{} n \log n$	$\mathcal{} n \log n$	$\mathcal{} n^2$	$\mathcal{} \log n$	Depends	Partitioning	Quicksort is usually done in place with O(log(n)) stack space.^{[citation needed]} Most implementations are unstable, as stable in-place partitioning is more complex. Naïve variants use an O(n) space array to store the partition.^{[citation needed]}
Merge sort	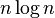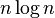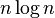$\mathcal{} {n \log n}$	$\mathcal{} {n \log n}$	$\mathcal{} {n \log n}$	Depends; worst case is $\mathcal{} n$	Yes	Merging	Highly parallelizable (up to O(log(n))) for processing large amounts of data.
In-place Merge sort	$\mathcal{} -$	$\mathcal{} -$	$\mathcal{} {n \left( \log n \right)^2}$	$\mathcal{} {1}$	Yes	Merging	Implemented in Standard Template Library (STL);^[2]can be implemented as a stable sort based on stable in-place merging.^[3]
Heapsort	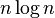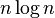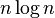$\mathcal{} {n \log n}$	$\mathcal{} {n \log n}$	$\mathcal{} {n \log n}$	$\mathcal{} {1}$	No	Selection
Insertion sort	$\mathcal{} n$	$\mathcal{} n^2$	$\mathcal{} n^2$	$\mathcal{} {1}$	Yes	Insertion	O(n + d), where d is the number of inversions
Introsort	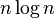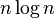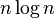$\mathcal{} n \log n$	$\mathcal{} n \log n$	$\mathcal{} n \log n$	$\mathcal{} \log n$	No	Partitioning & Selection	Used in SGI STL implementations
Selection sort	$\mathcal{} n^2$	$\mathcal{} n^2$	$\mathcal{} n^2$	$\mathcal{} {1}$	No	Selection	Stable with O(n) extra space, for example using lists.^[4] Used to sort this table in Safari or other Webkit web browser.^[5]
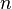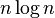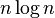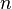Timsort	$\mathcal{} {n}$	$\mathcal{} {n \log n}$	$\mathcal{} {n \log n}$	$\mathcal{} n$	Yes	Insertion & Merging	$\mathcal{} {n}$ comparisons when the data is already sorted or reverse sorted.
Shell sort	$\mathcal{} n$	$\mathcal{} n (\log n)^2$ or $\mathcal{} n^{3/2}$	Depends on gap sequence; best known is 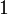$\mathcal{} n (\log n)^2$	$\mathcal{} 1$	No	Insertion
Bubble sort	$\mathcal{} n$	$\mathcal{} n^2$	$\mathcal{} n^2$	$\mathcal{} {1}$	Yes	Exchanging	Tiny code size
Binary tree sort	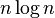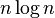$\mathcal{} n$	$\mathcal{} {n \log n}$	$\mathcal{} {n \log n}$	$\mathcal{} n$	Yes	Insertion	When using a self-balancing binary search tree
Cycle sort	—	$\mathcal{} n^2$	$\mathcal{} n^2$	$\mathcal{} {1}$	No	Insertion	In-place with theoretically optimal number of writes
Library sort	—	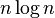$\mathcal{} {n \log n}$	$\mathcal{} n^2$	$\mathcal{} n$	Yes	Insertion
Patience sorting	—	—	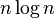$\mathcal{} n \log n$	$\mathcal{} n$	No	Insertion & Selection	Finds all the longest increasing subsequences within O(n log n)
Smoothsort	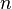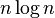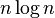$\mathcal{} {n}$	$\mathcal{} {n \log n}$	$\mathcal{} {n \log n}$	$\mathcal{} {1}$	No	Selection	An adaptive sort - 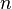$\mathcal{} {n}$ comparisons when the data is already sorted, and 0 swaps.
Strand sort	$\mathcal{} n$	$\mathcal{} n^2$	$\mathcal{} n^2$	$\mathcal{} n$	Yes	Selection
Tournament sort	—	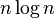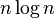$\mathcal{} n \log n$	$\mathcal{} n \log n$			Selection
Cocktail sort	$\mathcal{} n$	$\mathcal{} n^2$	$\mathcal{} n^2$	$\mathcal{} {1}$	Yes	Exchanging
Comb sort	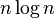$\mathcal{} n$	$\mathcal{} n \log n$	$\mathcal{} n^2$	$\mathcal{} {1}$	No	Exchanging	Small code size
Gnome sort	$\mathcal{} n$	$\mathcal{} n^2$	$\mathcal{} n^2$	$\mathcal{} {1}$	Yes	Exchanging	Tiny code size
Bogosort	$\mathcal{} n$	$\mathcal{} n \cdot n!$	$\mathcal{} {n \cdot n! \to \infty}$	$\mathcal{} {1}$	No	Luck	Randomly permute the array and check if sorted.
^[6]	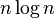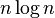$\mathcal{} -$	$\mathcal{} n \log n$	$\mathcal{} {n \log n}$	$\mathcal{} {1}$	Yes

Non-Comparison of algorithms

The following table describes integer sorting algorithms and other sorting algorithms that are not comparison sorts. As such, they are not limited by a $\Omega\left( {n \log n} \right)$ lower bound. Complexities below are in terms of n, the number of items to be sorted, k, the size of each key, and d, the digit size used by the implementation. Many of them are based on the assumption that the key size is large enough that all entries have unique key values, and hence that n << 2^k, where << means "much less than."

Non-comparison sorts Name Best Average Worst
Memory
Stable n << 2^k Notes

Pigeonhole sort	—	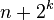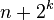$\;n + 2^k$	$\;n + 2^k$	$\;2^k$	Yes	Yes
Bucket sort (uniform keys)	—	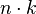$\;n+k$	$\;n^2 \cdot k$	$\;n \cdot k$	Yes	No	Assumes uniform distribution of elements from the domain in the array.^[7]
Bucket sort (integer keys)	—	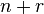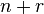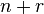$\;n+r$	$\;n+r$	$\;n+r$	Yes	Yes	r is the range of numbers to be sorted. If r = $\mathcal{O}\left( {n} \right)$ then Avg RT = $\mathcal{O}\left( {n} \right)$ ^[8]
Counting sort	—	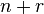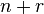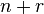$\;n+r$	$\;n+r$	$\;n+r$	Yes	Yes	r is the range of numbers to be sorted. If r = $\mathcal{O}\left( {n} \right)$ then Avg RT = $\mathcal{O}\left( {n} \right)$ ^[7]
LSD Radix Sort	—	$\;n \cdot \frac{k}{d}$	$\;n \cdot \frac{k}{d}$	$\mathcal{} n$	Yes	No	^[7]^[8]
MSD Radix Sort	—	$\;n \cdot \frac{k}{d}$	$\;n \cdot \frac{k}{d}$	$\mathcal{} n + \frac{k}{d} \cdot 2^d$	Yes	No	Stable version uses an external array of size n to hold all of the bins
MSD Radix Sort	—	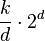$\;n \cdot \frac{k}{d}$	$\;n \cdot \frac{k}{d}$	$\frac{k}{d} \cdot 2^d$	No	No	In-Place. k / d recursion levels, 2^d for count array
Spreadsort	—	$\;n \cdot \frac{k}{d}$	$\;n \cdot \left( {\frac{k}{s} + d} \right)$	$\;\frac{k}{d} \cdot 2^d$	No	No	Asymptotics are based on the assumption that n << 2^k, but the algorithm does not require this.