交换排序（exchange sorts）算法大串讲

 

交换排序（exchange sorts）算法大串讲

本文内容框架：

§1 冒泡（Bubble Sort）排序及其改进

§2 鸡尾酒（Cocktail Sort）排序

  §3 奇偶（Odd-even Sort）排序

§4 快速（Quick Sort）排序及其改进

§5 梳（Comb Sort）排序

  §6 地精(Gnome Sort）排序

          §7 小结

 

 

 

§1 冒泡（Bubble Sort）排序及其改进

 

冒泡排序（Bubble Sort）

冒泡排序（Bubble Sort）是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

                                        

 

冒泡排序算法的步骤：

1.比较相邻的元素。如果第一个比第二个大，就交换他们两个。

2.对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。

3.针对所有的元素重复以上的步骤，除了最后一个。

4.持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

 

#include <stdio.h>
   void bubbleSort(int arr[], int count)
   {
       int i = count, j;
       int temp;
 
       while(i > 0)
       {
          for(j = 0; j < i - 1; j++)
          {
              if(arr[j] > arr[j + 1])
              {   temp = arr[j];
                  arr[j] = arr[j + 1];
                  arr[j + 1] = temp;
              }
          }
          i--;
      }
  }
 
  int main(int arc, char* const argv[])
  {
      //测试数据
      int arr[] = {5, 4, 1, 3, 6};
      //冒泡排序
      bubbleSort(arr, 5);
      //打印排序结果
      int i;
      for(i = 0; i < 5; i++)
          printf("%4d", arr[i]);
 }

 

 

冒泡排序算法最坏情况和平均复杂度是O(n²)，甚至连插入排序（O(n²)算法复杂度）效率都比冒泡排序算法更好，唯一的优势在于基于它的改进算法——快速排序算法。

 

冒泡排序算法改进

 

    　上述的冒泡排序还可做如下的改进：

(1)记住最后一次交换发生位置index的冒泡排序

1.设置一标志性变量index, 用于记录每趟排序中最后一次进行交换的位置。由于index位置之后的记录均已交换到位, 故在进行下一趟排序时只要扫描到pos位置即可。

 

 void bubbleSort1(int arr[], int count)
   {
       int i = count, j;
       int temp;
       int index=i;
       while(i > 0)
       {
          for(j = 0; j < index-1; j++)
          {
              if(arr[j] > arr[j + 1])
              {   temp = arr[j];
                  arr[j] = arr[j + 1];
                  arr[j + 1] = temp;
                   index=j;
              }
          }
          i--;
      }
  }

 

  2.如果某一趟没有数据交换，则表示已经排好序，就可以提前终止循环。

 

 void bubbleSort2(int arr[], int count)
   {
       int i = count, j;
       int temp;
       bool isExchange=true;
       while(i > 0&&isExchange)
       {
          isExchange=false;
          for(j = 0; j < i - 1; j++)
          {
              if(arr[j] > arr[j + 1])
              {   temp = arr[j];
                  arr[j] = arr[j + 1];
                  arr[j + 1] = temp;
                  isExchange=true;
              }
          }
          i--;
      }
  }

 当然上述两种改进方法可以同时使用……

 

 

 

(2) 改变扫描方向的冒泡排序（其实就是鸡尾酒排序算法）

 ①冒泡排序的不对称性

　　能一趟扫描完成排序的情况：

    　只有最轻的气泡位于R[n]的位置，其余的气泡均已排好序，那么也只需一趟扫描就可以完成排序。

【例】对初始关键字序列12，18，42，44，45，67，94，10就仅需一趟扫描。

需要n-1趟扫描完成排序情况：

　    当只有最重的气泡位于R[1]的位置，其余的气泡均已排好序时，则仍需做n-1趟扫描才能完成排序。

【例】对初始关键字序列：94，10，12，18，42，44，45，67就需七趟扫描。

 

②造成不对称性的原因

　　每趟扫描仅能使最重气泡"下沉"一个位置，因此使位于顶端的最重气泡下沉到底部时，需做n-1趟扫描。

 

③改进不对称性的方法

    　在排序过程中交替改变扫描方向，可改进不对称性。

 

 void bubbleSort3(int arr[], int count)
   {
       int hight= count-1, low=0,j;
       int temp;
       int index=low
       while(high> low)
       {
          for(j = low; j < high; j++)
          {
              if(arr[j] > arr[j + 1])
              {   temp = arr[j];
                  arr[j] = arr[j + 1];
                  arr[j + 1] = temp;
                  index=j;
              }
          }
          high=index;
          for(j = high; j > low; j--)
          {
              if(arr[j] > arr[j - 1])
              {   temp = arr[j];
                  arr[j] = arr[j - 1];
                  arr[j - 1] = temp;
                  index=j;
              }
          }
          low=index;
      } 
  }

 

 

§2 鸡尾酒（Cocktail Sort）排序

 

鸡尾酒排序（cocktai sort）算法

鸡尾酒排序等于是冒泡排序的轻微变形。不同的地方在于扫描方向是从低到高然后从高到低，而冒泡排序则仅从低到高去比较序列里的每个元素。他可以得到比冒泡排序稍微好一点的效能，原因是冒泡排序只从一个方向进行比对(由低到高)，每次循环只移动一个项目。

鸡尾酒排序最糟或是平均所花费的次数都是，但如果序列在一开始已经大部分排序过的话，会接近。鸡尾酒排序最糟或是平均所花费的次数都是，但如果序列在一开始已经大部分排序过的话，会接近。

 

void CockTail(int arr[],int count)
{
	int  bottom = 0;
	int  top = count-1;
	bool flag = true;
    
	while(flag)
	{
		flag=false;
		for(int i=bottom;i<top;i++)
		{
			if(arr[i]>arr[i+1])
			{
				swap(arr[i],arr[i+1]);
				flag=true;
			}
		}
		
		top--;

		for(int j=top;j>bottom;j--)
		{
			if(arr[j-1]>arr[j])
			{
				swap(arr[j-1],arr[j]);
				flag=true;
			}	

		}

		bottom++;
	}
}

 

 

§3 奇偶(Even-old Sort）排序

 

奇偶排序（Odd-even sort）算法

该算法中，通过比较数组中相邻的（奇-偶）位置数字对，如果该奇偶对是错误的顺序（第一个大于第二个），则交换。下一步重复该操作，但针对所有的（偶-奇）位置数字对。如此交替进行下去。

 

void oddEvenSort(int *pArr, const int length)
{
        int i, tmp;
        bool sorted =false;
        while(!sorted)
        {
                sorted=true;
                for(i=1; i<length-1; i+=2)
                {
                        if(*(pArr+i)>*(pArr+i+1))
                        {
                                sorted=false;
                                tmp=*(pArr+i);
                                *(pArr+i)=*(pArr+i+1);
                                *(pArr+i+1)=tmp;
                        }
                }

                for(i=0; i<length-1; i+=2)
                {
                        if(*(pArr+i)>*(pArr+i+1))
                        {
                                sorted=false;
                                tmp=*(pArr+i);
                                *(pArr+i)=*(pArr+i+1);
                                *(pArr+i+1)=tmp;
                        }
                }
        }
}

 

 

§4 快速（Quick Sort）排序

 

快速排序（quick sort）算法

快速排序是冒泡排序的一种改进，冒泡排序排完一趟是最大值冒出来了，那么可不可以先选定一个值，然后扫描待排序序列，把小于该值的记录和大于该值的记录分成两个单独的序列，然后分别对这两个序列进行上述操作。这就是快速排序，我们把选定的那个值称为枢纽值，如果枢纽值为序列中的最大值，那么一趟快速排序就变成了一趟冒泡排序。

 

 

快速排序使用分治法（Divide and conquer）策略来把一个串行（list）分为两个子串行（sub-lists）。

步骤为：

从数列中挑出一个元素，称为 "基准"（pivot），

重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。

递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会退出，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

 

//快速排序（两端交替着向中间扫描）
void quickSort1(int *a,int low,int high)
{
	int pivotkey=a[low];//以a[low]为枢纽值
	int i=low,j=high;
	if(low>=high)
		return;
	//一趟快速排序
	while(i<j){//双向扫描
		while(i < j && a[j] >= pivotkey)
			j--;
		a[i]=a[j];
		while(i < j && a[i] <= pivotkey)
			i++;
		a[j]=a[i];
	}
	a[i]=pivotkey;//放置枢纽值
	//分别对左边、右边排序
    quickSort1(a,low,i-1); 
	quickSort1(a,i+1,high); 
}

//快速排序（以最后一个记录的值为枢纽值，单向扫描数组）
void quickSort2(int *a,int low,int high)
{
	int pivotkey=a[high];//以a[high]为枢纽值
    int i=low-1,temp,j;
	if(low>=high)
		return;
	//一趟快速排序
	for(j=low;j<high;j++){
		if(a[j]<=pivotkey){
			i++;
            temp=a[i];
			a[i]=a[j];
			a[j]=temp;
		}
	}
	i++;
	//放置枢纽值
	temp=a[i];
	a[i]=pivotkey;
	a[high]=temp;
	//分别对左边、右边排序
    quickSort2(a,low,i-1); 
	quickSort2(a,i+1,high); 
}

 

 

快速排序算法的几种改进

1.随机化算法

基本的快速排序选取第一个元素作为主元。这样在数组已经有序的情况下，每次划分将得到最坏的结果。一种比较常见的优化方法是随机化算法，即随机选取一个元素作为主元。这种情况下虽然最坏情况仍然是O(n^2)，但最坏情况不再依赖于输入数据，而是由于随机函数取值不佳。实际上，随机化快速排序得到理论最坏情况的可能性仅为1/(2^n)。所以随机化快速排序可以对于绝大多数输入数据达到O(nlogn)的期望时间复杂度

　　随机化快速排序的唯一缺点在于，一旦输入数据中有很多的相同数据，随机化的效果将直接减弱。对于极限情况，即对于n个相同的数排序，随机化快速排序的时间复杂度将毫无疑问的降低到O(n^2)。

2. 三平均分区法

   与一般的快速排序方法不同，它并不是选择待排数组的第一个数作为中轴，而是选用待排数组最左边、最右边和最中间的三个元素的中间值作为中轴。这一改进对于原来的快速排序算法来说，主要有两点优势：

   （1） 首先，它使得最坏情况发生的几率减小了。

   （2） 其次，未改进的快速排序算法为了防止比较时数组越界，在最后要设置一个哨点。如果在分区排序时，中间的这个元素（也即中轴）是与最右边数过来第二个元素进行交换的话，那么就可以省略与这一哨点值的比较。

关于这一改进还有更进一步的改进，在继续的改进中不仅仅是为了选择更好的中轴才进行左中右三个元素的的比较，它同时将这三个数排好序后按照其顺序放回待排数组，这样就能够保证一个长度为n的待排数组在分区之后最长的子分区的长度为n-2，而不是原来的n-1。也可以在选取中轴值时，可以从由左中右三个中选取扩大到五个元素中或者更多元素中选取，一般的，会有（2t＋1）平均分区法（median-of-(2t+1)，三平均分区法英文为median-of-three）。

3. 根据分区大小调整算法

    减少递归栈使用的优化，快速排序的实现需要消耗递归栈的空间，而大多数情况下都会通过使用系统递归栈来完成递归求解。对系统栈的频繁存取会影响到排序的效率。

快速排序对于小规模的数据集性能不是很好。没有插入性能高。

快速排序算法使用了分治技术，最终来说大的数据集都要分为小的数据集来进行处理。

当数据集较小时，不必继续递归调用快速排序算法，使用插入排序代替快速排序。STL中sort就是用的快排+插入排序的，使得最坏情况下的时间复杂度也是O(nlgn)．这一改进被证明比持续使用快速排序算法要有效的多。

4. 不同的分区方案考虑

    对于快速排序算法来说，实际上大量的时间都消耗在了分区上面，因此一个好的分区实现是非常重要的。尤其是当要分区的所有的元素值都相等是，一般的快速排序算法就陷入了最坏的一种情况，也即反复的交换相同的元素并返回最差的中轴值。无论是任何数据集，只要它们中包含了很多相同的元素的话，这都是一个严重的问题，因为许多“底层”的分区都会变得完全一样。

    对于这种情况的一种改进办法就是将分区分为三块而不是原来的两块：一块是小于中轴值的所有元素，一块是等于中轴值的所有元素，另一块是大于中轴值的所有元素。另一种简单的改进方法是，当分区完成后，如果发现最左和最右两个元素值相等的话就避免递归调用而采用其他的排序算法来完成。

5. 使用多线程：快速排序是分而治之的思想，每个独立的段可以并行进行排序。因此可以利用计算机的并行处理能力来提高排序的性能；

    在大多数情况下，创建一个线程所需要的时间要远远大于两个元素比较和交换的时间，因此，快速排序的并行算法不可能为每个分区都创建一个新的线程。一般来说，会在实现代码中设定一个阀值，如果分区的元素数目多于该阀值的话，就创建一个新的线程来处理这个分区的排序，否则的话就进行递归调用来排序。

 

 

总的来说，对于快速排序算法的改进主要集中在三个方面：

1 选取一个更好的中轴值

2 根据产生的子分区大小调整算法

3 不同的划分分区的方法

 

 

§5 梳（Comb Sort）排序

 

梳排序(Comb sort)算法

 

梳排序是改良自冒泡排序和快速排序，在冒泡排序中，只比较阵列中相邻的二项，即比较的二项的间距(Gap)是1，梳排序提出此间距其实可大于1，改自插入排序的希尔排序同样提出相同观点。梳排序中，开始时的间距设定为阵列长度，并在循环中以固定比率递减，通常递减率设定为1.3。在一次循环中，梳排序如同泡沫排序一样把阵列从首到尾扫描一次，比较及交换两项，不同的是两项的间距不固定于1。如果间距递减至1，梳排序假定输入阵列大致排序好，并以冒泡排序作最后检查及修正。O(n*logn)时间复杂度，O(1)空间复杂度，属于不稳定的排序算法。

 

 

 

 

 

void combsort(int *arr, int size) {
 
  float shrink_factor = 1.247330950103979;
  int gap = size, swapped = 1, swap, i;
 
  while ((gap > 1) || swapped) {
    if (gap > 1) gap = gap / shrink_factor;
 
    swapped = 0; 
    i = 0;
 
    while ((gap + i) < size) {
      if (arr[i] - arr[i + gap] > 0) {
        swap = arr[i];
        arr[i] = arr[i + gap];
        arr[i + gap] = swap;
        swapped = 1;
      }
      ++i;
    }
  }
}

 

梳排序算法举例：

假设输入为 8 4 3 7 6 5 2 1

目标为将之变成递增排序。 因为输入长度=8，开始时设定间距为8÷1.3≒6， 则比较8和2、4和1，并作交换两次。

8 4 3 7 6 5 2 1

2 4 3 7 6 5 8 1

2 1 3 7 6 5 8 4

第二次循环，更新间距为6÷1.3≒4。比较2和6、1和5，直至7和4，此循环中只须交换一次。

2 1 3 7 6 5 8 4

2 1 3 4 6 5 8 7

接下来的每次循环，间距依次递减为3 → 2 → 1，

间距=3时，不须交换

2 1 3 4 6 5 8 7

间距=2时，不须交换

2 1 3 4 6 5 8 7

间距h=1时，交换三次

2 1 3 4 6 5 8 7

1 2 3 4 6 5 8 7

1 2 3 4 5 6 8 7

1 2 3 4 5 6 7 8

上例中，共作了六次交换以完成排序。 

 

 

§6 地精(Gnome Sort）排序

 

地精排序(Gnome Sort) 算法

地精排序也叫侏儒排序，是最简单的一种排序算法，它的概念很简单，无需嵌套循环。它的运行时间是Ø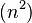，但如果列表最初几乎排序趋于O（Ñ）。直接看代码：

 

void gnomesort(int n, int ar[]) {
    int i = 0;
 
    while (i < n) {
       if (i == 0 || ar[i-1] <= ar[i]) i++;
       else {int tmp = ar[i]; ar[i] = ar[i-1]; ar[--i] = tmp;}
    }
}

 

 写成C++模板函数

 

template<class T>
void gnome_sort_1(T data[], int n, bool comparator(T, T))
{
    int i = 1;
    while (i < n)
    {
       if (i > 0 && comparator(data[i], data[i-1]))
       {
           swap(data[i], data[i-1]);
           i--;
       }else
       {
           i++;
       }
    }
}

 

下面直接给出两个改进版本，读者可以自行体会：

 

template<class T>
void gnome_sort_2(T data[], int n, bool comparator(T, T))
{
    int i = 1, previous_position = -1;
    while (i < n)
    {
       if (i > 0 && comparator(data[i], data[i-1]))
       {
           // Mark the Gnome's previous position before traverse backward
           if (previous_position == -1)
           {
              previous_position = i;
           }
           swap(data[i], data[i-1]);
           i--;
       }else
       {
           if (previous_position == -1)
           {
              i++;
           }else
           {
              // After traverse backward, go to the position next to the previous
              i = previous_position + 1;
              previous_position = -1;
           }
       }
    }
}

 

 

template<class T>
void gnome_sort_3(T data[], int n, bool comparator(T, T))
{
    int i = 0, previous_position = -1;
    T temp;
    while (i < n)
    {
       if (i > 0 && comparator(temp, data[i-1]))
       {
           // Mark the Gnome's previous position before traverse backward
           if (previous_position == -1)
           {
              previous_position = i;
           }
           data[i] = data[i-1];
           i--;
       }else
       {
           if (previous_position == -1)
           {
              i++;
           }else
           {
              // Put the previous value here
              data[i] = temp;
              // After traverse backward, go to the position next to the previous
              i = previous_position + 1;
              previous_position = -1;
           }
           temp = data[i];
       }
    }
}

 

§7 小结

这篇博文列举了选择排序的7个算法，基本可以掌握其中概要，管中窥豹，不求甚解。如果你有任何建议或者批评和补充，请留言指出，不胜感激，更多参考请移步互联网。

 

 

 

参考：

①einstein991225： http://blog.csdn.net/einstein991225/article/details/7957077

②love__coder： http://blog.csdn.net/love__coder/article/details/7914819

③winark： http://blog.csdn.net/winark/article/details/5918944

④更多参考来着维基百科

 

 

 

 

 

评论

2 楼 DSQiu 2012-10-29  

闪闪4521 写道

这几个GIF让人眼前一亮啊，楼主牛B

我之前也没怎么看明白，后来也发现这个图片的真谛，不过这些图片都是维基百科上的，不是作者原创，贴过来就是想有一个很直观的理解……

1 楼 闪闪4521 2012-10-29  

这几个GIF让人眼前一亮啊，楼主牛B