多个圆环组成的区域的合并

最近很忙，忙的连写日记的功夫都没有了。

有个项目的需求是需要把多个圆环的区域合并。得到包络线和内部空洞的线。

查了查google。类似的实现比较少见。简单的说说我的实现方法。

基本想法就是通过判断一段圆弧和圆环组的关系，来判断这段圆弧是否是属于合并后的包络线的一部分

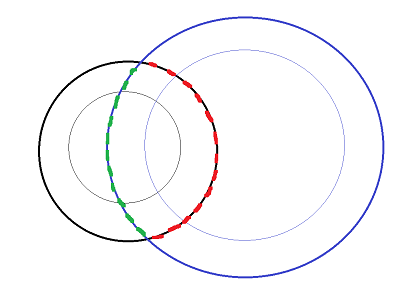
如图，左边的圆盒右边的圆相交。则这两个圆就被分成了两段。

对外包络线，如上图。将所有圆环的外圆（粗线）相交。把每个圆都切成一段段的圆弧，如左边的黑色圆，则切成了黑色段和黑色+红色的两段。对每一段，我们测试这一段弧是否在其它圆环的大圆内部，如果这段圆弧不在其它的环的大圆内部（不包括内部小圆），则这段圆弧属于外包络线的一部分。否则不是。

内部透空的小圆的合并稍微麻烦一些。因为透空的部分，不光是小圆的弧，还会有大圆弧的参与。

考察小圆的圆弧，同样的，我们将小圆 和其它圆环的求交点，把小圆切成一段段的弧线（注意小圆和其它环求交的时候，就要跟这个环的大小圆都交一遍，而不光是小圆和小圆了）。如果这一段弧线不在这组圆环内（指的是环的内部，而不是大圆的内部），则表示这段弧是属于内包络线的一部分。

考察大圆的弧，大圆产生内包络线的原因主要是大圆会抵消一部分小圆的透空作用。所以同样的我们将大圆 和其它圆环的求交点，把小圆切成一段段的弧线--跟外包络不同，这次求交的时候，该大圆要和其它圆环的大小圆都求交，而不光是大圆对大圆。 对每一段圆弧，如果弧线不在环的内部，而且该段弧应该还需要位于某个环的小圆内部（看图就明白为什么了）。则该大圆弧也是内包络的一部分。

这里求圆弧在环的内部还是在大小圆内，有一个偷懒的方法。因为我们已经保证这段圆弧除了两个端点以外不和其它任何弧相交，所以只要用这段弧的中点来代替弧来作判断就好了。使得复杂性大大降低了。

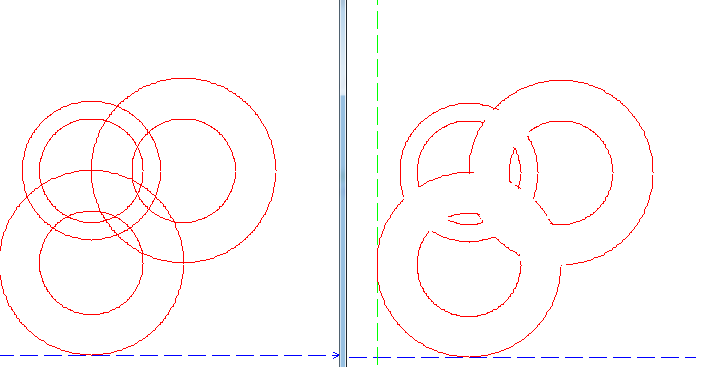
以上是效果图，三个环合并成一个区域。

以下是主要代码

class CRingGroup
{
public:
bool load(const wchar_t* _ringGroupsFile)
{
xXmlDocument doc;
if(doc.load(_ringGroupsFile) == false )
return false;

xXmlNode::XmlNodes ringNodes;
doc.findAllNode(L"ring" , ringNodes);
if(ringNodes.size() == 0)
return false;

for(size_t i = 0 ; i < ringNodes.size() ; i ++)
{
xXmlNode* pNode = ringNodes[i];
xRing _ring;
_ring.m_InnerR = pNode->float_value(L"r1");
_ring.m_OutR = pNode->float_value(L"r2");
_ring.m_Center = pNode->get_value<float2>(L"center");
m_vRings.push_back(_ring);
}
}

void toSplineDrawer(CSplineDraw& drawer)
{
drawer.m_vArcs.clear();
for(int i = 0 ; i < m_vRings.size() ; i ++)
{
std::vector<float> CutPoints;
xRing& ring = m_vRings[i];
ring.toArcs(CutPoints , true , drawer.m_vArcs);
}

for(int i = 0 ; i < m_vRings.size() ; i ++)
{
std::vector<float> CutPoints;
xRing& ring = m_vRings[i];
ring.toArcs(CutPoints , false , drawer.m_vArcs);
}
}

void toInnerLine(std::vector<xArc>& vOut)
{
for(int i = 0 ; i < m_vRings.size() ; i ++)
{
std::vector<float> vCutPoints;
std::vector<xArc> vArcs;

//先来切内圆
xRing& _ring = m_vRings[i];
for(int j = 0 ; j < m_vRings.size() ; j ++)
{
if(j == i) continue;
xRing& _ring2 = m_vRings[j];
_ring.CutByCircle(_ring2.m_Center , _ring2.m_OutR , vCutPoints , false );
_ring.CutByCircle(_ring2.m_Center , _ring2.m_InnerR , vCutPoints , false);
}

_ring.toArcs(vCutPoints , false , vArcs);

//内圆的弧，必须在所有的外圆的外部。
for(int iArc = 0 ; iArc < vArcs.size() ; iArc ++)
{
xArc& _arc = vArcs[iArc];
bool bInRing = false;
for(int k = 0 ; k < m_vRings.size() ; k ++)
{
if( k == i ) continue;
xRing& _ring2 = m_vRings[k];
if( true == _ring2.IsInRing( _arc ) )
{
bInRing = true;
}
}

//////////////////////////////////////////////////////////////////////////
if(bInRing == false)
{
vOut.push_back(_arc);
}
}

//内圆切完了。来切外圆套在其它内圆中的部分。
vCutPoints.clear();
vArcs.clear();
for(int j = 0 ; j < m_vRings.size() ; j ++)
{
if(j == i) continue;
xRing& _ring2 = m_vRings[j];
_ring.CutByCircle(_ring2.m_Center , _ring2.m_OutR , vCutPoints , true );
_ring.CutByCircle(_ring2.m_Center , _ring2.m_InnerR , vCutPoints , true);
}

_ring.toArcs(vCutPoints , true , vArcs);

//内圆的弧，必须在所有的外圆的外部。
for(int iArc = 0 ; iArc < vArcs.size() ; iArc ++)
{
xArc& _arc = vArcs[iArc];
bool bInRing = false;
bool bInSmallRing = false;
for(int k = 0 ; k < m_vRings.size() ; k ++)
{
if( k == i ) continue;
xRing& _ring2 = m_vRings[k];
if( true == _ring2.IsInRing( _arc ) )
{
bInRing = true;
}

if( true == _ring2.IsInSmallRing( _arc) )
{
bInSmallRing = true;
}
}

//////////////////////////////////////////////////////////////////////////
if(bInRing == false && bInSmallRing == true)
{
vOut.push_back(_arc);
}
}
}
return ;
}

void toOutLine(std::vector<xArc>& vOut)
{
//return ;
for(int i = 0 ; i < m_vRings.size() ; i ++)
{
std::vector<float> vCutPoints;
xRing& _ring = m_vRings[i];
for(int j = 0 ; j < m_vRings.size() ; j ++)
{
if(j == i) continue;
xRing& _ring2 = m_vRings[j];
_ring.CutByCircle(_ring2.m_Center , _ring2.m_OutR , vCutPoints , true);

}

std::vector<xArc> vArcs;
_ring.toArcs(vCutPoints , true , vArcs);

//判断生成的圆弧是不是在内部。
for(int iArc = 0 ; iArc < vArcs.size() ; iArc ++)
{
xArc& _arc = vArcs[iArc];
bool bInRing = false;
for(int k = 0 ; k < m_vRings.size() ; k ++)
{
if( k == i ) continue;
xRing& _ring2 = m_vRings[k];
if( true == _ring2.IsInOutRing(_arc ) )
{
bInRing = true;
}
}

//////////////////////////////////////////////////////////////////////////
if(bInRing == false)
{
vOut.push_back(_arc);
}
}
}
return ;
}
public:
std::vector<xRing> m_vRings;
};