从零实现3D图像引擎：(5)3D坐标系函数库

1. 数学分析

1) 2D笛卡尔坐标系与2D极坐标系

2D笛卡尔坐标系就是平面直角坐标系，不说了。

2D极坐标系，是用方向和距离来定义2D空间中的点，而非x,y坐标，如下图：

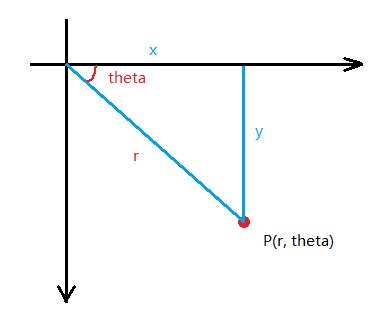
其中极坐标的参数用红色表示，笛卡尔坐标的参数用蓝色字表示。

非常显而易见，他们之间的转换关系如下：

x = r * cos(theta)

y = r * sin(theta)

r = sqrt(x2 + y2)

theta = arctg(y/x)

2) 3D笛卡尔坐标系

在2D笛卡尔坐标系上增加了Z轴，形成3D笛卡尔坐标系。分为左手坐标系和右手坐标系。区分方法：用左手握住Z轴，大拇指伸直，其他四指的指尖方向从X轴转向Y轴，如果大拇指的指向是Z的正半轴，则为左手坐标系，反之为右手。

3) 3D柱面坐标系

3D柱面坐标系和2D的极坐标系对应，只是在2D极坐标系上增加了一条Z轴，所以3D笛卡尔坐标系与3D柱面坐标系的转换也非常简单：x和y以及r和theta都不变，只增加了Z坐标而已。3D柱面坐标系的表示方式是：P(r, theta, z)。

4) 3D球面坐标系

这个是3D坐标系中最复杂的，用P(p, phi, theta)表示。其中p是点P到原点的距离，phi是原点到点P的直线与正Z轴的夹角，theta是原点到点P的线段在X-Y平面上的投影与X轴之间的夹角，其实正好是极坐标theta。由于比较复杂，如图所示：

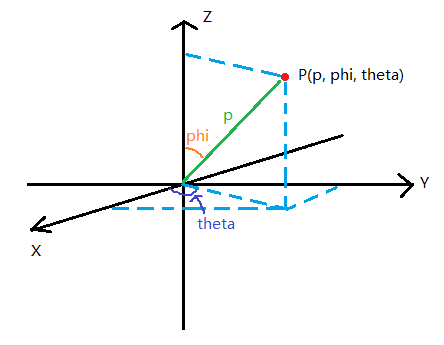
现在可以推导一下(p,phi,theta)与(x,y,z)的关系了。

由图上可以得知:

OP在X-Y平面上的投影长度r = sqrt(x2+y2)

p = sqrt(x2+y2+z2)

Sin(phi) = r / p,所以

phi = arcsin(r / p)

tg(theta) = y / x

theta = arctg(y/x)

从p,phi,theta如何得到x,y,z呢：

r = p * Sin(phi)

x = r * Cos(theta)

y = r * Sin(theta)

z = p * Cos(phi)

代入整理得：

x = p * Sin(phi) * Cos(theta)

y = p * Sin(phi) * Sin(theta)

z = p * Cos(phi)

弄清楚了上面的关系，就可以建立这些坐标系下点的数据结构，以及转换函数了。

2. 代码实现

1) 结构体定义

// 类型声明
typedef struct POINT2D_TYPE // 2D笛卡尔坐标
{
	double x;
	double y;
} POINT2D, *POINT2D_PTR;

typedef struct POINT3D_TYPE // 3D笛卡尔坐标
{
	double x;
	double y;
	double z;
} POINT3D, *POINT3D_PTR;

typedef struct POLAR2D_TYPE // 2D极坐标
{
	double r;
	double theta;
} POLAR2D, *POLAR2D_PTR;

typedef struct CYLINDRICAL3D_TYPE // 3D柱面坐标
{
	double r;
	double theta;
	double z;
} CYLINDRICAL3D, *CYLINDRICAL3D_PTR;

typedef struct SPHERICAL3D_TYPE
{
	double p;
	double phi;
	double theta;
} SPHERICAL3D, *SPHERICAL_PTR;

2) 转换函数定义

void _CPPYIN_Math::CooTransPOINT2DtoPOLAR2D(POINT2D_PTR point2d, POLAR2D_PTR polar2d)
{
	polar2d->r = sqrt((point2d->x * point2d->x) + (point2d->y * point2d->y));
	polar2d->theta = atan((point2d->y) / (point2d->x));
}

void _CPPYIN_Math::CooTransPOLAR2DtoPOINT2D(POLAR2D_PTR polar2d, POINT2D_PTR point2d)
{
	point2d->x = polar2d->r * cos(polar2d->theta);
	point2d->y = polar2d->r * sin(polar2d->theta);
}

void _CPPYIN_Math::CooTransPOINT3DtoCYLINDRICAL3D(POINT3D_PTR point3d, CYLINDRICAL3D_PTR cylindrical3d)
{
	cylindrical3d->r = sqrt((point3d->x * point3d->x) + (point3d->y * point3d->y));
	cylindrical3d->theta = atan((point3d->y) / (point3d->x));
	cylindrical3d->z = point3d->z;
}

void _CPPYIN_Math::CooTransCYLINDRICAL3DtoPOINT3D(CYLINDRICAL3D_PTR cylindrical3d, POINT3D_PTR point3d)
{
	point3d->x = cylindrical3d->r * cos(cylindrical3d->theta);
	point3d->y = cylindrical3d->r * sin(cylindrical3d->theta);
	point3d->z = cylindrical3d->z;
}

void _CPPYIN_Math::CooTransPOINT3DtoSPHERICAL3D(POINT3D_PTR point3d, SPHERICAL3D_PTR spherical3d)
{
	spherical3d->p = sqrt((point3d->x * point3d->x) + (point3d->y * point3d->y) + (point3d->z * point3d->z));
	double r = sqrt((point3d->x * point3d->x) + (point3d->y * point3d->y));
	spherical3d->phi = asin(r / spherical3d->p);
	spherical3d->theta = atan(point3d->y / point3d->x);
}

void _CPPYIN_Math::CooTransSPHERICAL3DtoPOINT3D(SPHERICAL3D_PTR spherical3d, POINT3D_PTR point3d)
{
	double r = spherical3d->p * sin(spherical3d->phi);
	point3d->x = r * cos(spherical3d->theta);
	point3d->y = r * sin(spherical3d->theta);
	point3d->z = spherical3d->p * cos(spherical3d->phi);
}

没什么可说的，全是套上面推出来的公式而已。

3. 代码下载

完整项目源代码下载：>>点击进入下载页<<