- 浏览: 4432287 次
- 性别:

- 来自: 湛江
-

博客专栏
-

-
SQLite源码剖析
浏览量:80376
-

-
WIN32汇编语言学习应用...
浏览量:70860
-

-
神奇的perl
浏览量:104126
-

-
lucene等搜索引擎解析...
浏览量:287658
-

-
深入lucene3.5源码...
浏览量:15156
-

-
VB.NET并行与分布式编...
浏览量:68412
-

-
silverlight 5...
浏览量:32594
-

-
算法下午茶系列
浏览量:46295
最新评论
-
yoyo837:
counters15 写道目前只支持IE吗?插件的东西是跨浏览 ...
Silverlight 5 轻松开启绚丽的网页3D世界 -
shuiyunbing:
直接在前台导出方式:excel中的单元格样式怎么处理,比如某行 ...
Flex导出Excel -
di1984HIT:
写的很好~
lucene入门-索引网页 -
rjguanwen:
在win7 64位操作系统下,pygtk的Entry无法输入怎 ...
pygtk-entry -
ldl_xz:
http://www.9958.pw/post/php_exc ...
PHPExcel常用方法汇总(转载)
![deepfuture的博客: 深未来(深度创造未来)[deepfuture@yeah.net] deepfuture的博客](https://www.iteye.com/upload/logo/user/690059/d08c7f3a-9298-3a06-9235-0d0226833f0a.jpg?1717538039)

 。若
。若  在点
在点 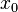 的某个邻域内有定义,则当自变量
的某个邻域内有定义,则当自变量 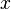 在
在 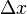 (点
(点  仍在该邻域内)时,相应地函数
仍在该邻域内)时,相应地函数  取得增量
取得增量 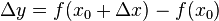 ;如果
;如果 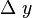 与
与 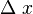 之比当
之比当  时的极限存在,则称函数
时的极限存在,则称函数  在点
在点 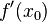 ,即:
,即:
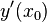 、
、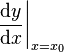 、
、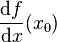 或
或  。
。 处的导数也可以定义为:当定义域内的变量
处的导数也可以定义为:当定义域内的变量  趋近于
趋近于 
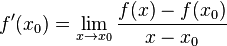
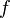 的自变量在一点
的自变量在一点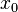 上产生一个增量
上产生一个增量 时,函数输出值的增量与自变量增量
时,函数输出值的增量与自变量增量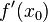 、
、
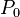 为曲线上的一个定点,
为曲线上的一个定点,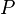 为曲线上的一个动点。当
为曲线上的一个动点。当 的极限位置
的极限位置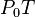 存在,则称
存在,则称 的图像,那么割线
的图像,那么割线
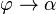 ,则
,则 为:
为:
 ,因此,导数的几何意义即曲线
,因此,导数的几何意义即曲线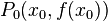 处切线的斜率
处切线的斜率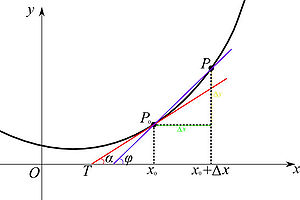
 在其定义域包含的某区间
在其定义域包含的某区间  内每一个点都可导,那么也可以说函数
内每一个点都可导,那么也可以说函数 的一个确定的导数值,如此一来就构成了一个新的函数
的一个确定的导数值,如此一来就构成了一个新的函数 ,这个函数称作原来函数
,这个函数称作原来函数  、
、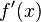 或者
或者 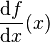 ,通常也可以说导函数为导数
,通常也可以说导函数为导数 ,换句话说,函数的微分与自变量的微分之商等于该函数的导数。因此,导数也叫做微商。于是函数
,换句话说,函数的微分与自变量的微分之商等于该函数的导数。因此,导数也叫做微商。于是函数
 的自变量
的自变量 有一个微小的改变
有一个微小的改变 时,函数的变化可以分解为两个部分。一个部分是线性部分:在一维情况下,它正比于自变量的变化量
时,函数的变化可以分解为两个部分。一个部分是线性部分:在一维情况下,它正比于自变量的变化量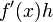 或
或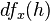 。如果一个函数在某处具有以上的性质,就称此函数在该点可微。
。如果一个函数在某处具有以上的性质,就称此函数在该点可微。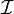 内有定义。对于
内有定义。对于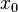 ,当
,当 (也在此区间内)时。如果函数的增量
(也在此区间内)时。如果函数的增量 可表示为
可表示为  (其中
(其中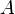 是不依赖于
是不依赖于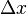 的常数),而
的常数),而 是比
是比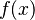 在点
在点 称作函数在点
称作函数在点 ,即
,即 ,
, 的线性主部。
的线性主部。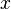 的增量
的增量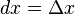 。
。
 很小时,
很小时, 比
比 要小得多(高阶无穷小),因此在点
要小得多(高阶无穷小),因此在点 如果满足如下性质:
如果满足如下性质:
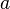 被称为
被称为  时的无穷小量
时的无穷小量 为两个序列,而且都是
为两个序列,而且都是  趋于无穷时都趋于零,但趋于零的速度是有区别的。可以用如下方式比较它们的速度:
趋于无穷时都趋于零,但趋于零的速度是有区别的。可以用如下方式比较它们的速度: ,存在正整数
,存在正整数  使得
使得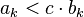
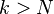 时总是成立,则称
时总是成立,则称 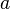 是
是 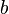 的高阶无穷小,记作
的高阶无穷小,记作
 表示实数域。对任意一个正整数n,实数的n元组的全体构成了
表示实数域。对任意一个正整数n,实数的n元组的全体构成了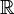 上的一个n维向量空间,用
上的一个n维向量空间,用 来表示。有时称之为实数坐标空间。
来表示。有时称之为实数坐标空间。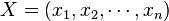 ,这里的
,这里的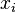 都是实数。
都是实数。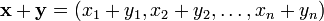

 、
、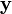 ,引入它们的“标准内积”
,引入它们的“标准内积” (一些文献上称为点积,记为
(一些文献上称为点积,记为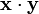 ):
): 。
。

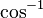 为反余弦函数。
为反余弦函数。 。
。 来标记之。欧氏结构使
来标记之。欧氏结构使
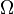 射到Rm的一个函数。对于
射到Rm的一个函数。对于 中的点
中的点 。如果存在线性映射
。如果存在线性映射
 。
。
 的线性主部,记为
的线性主部,记为 。例如,对于二元函数
。例如,对于二元函数 ,设f在点
,设f在点 的某个邻域内有定义,
的某个邻域内有定义, 为该邻域内的任意一点,则该函数在点
为该邻域内的任意一点,则该函数在点 ,
, 仅与
仅与 有关,而与
有关,而与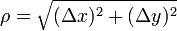 。若
。若 是当
是当 时的高阶无穷小,则称此函数
时的高阶无穷小,则称此函数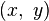 可微分,而
可微分,而 即为函数
即为函数
 。
。
 。
。

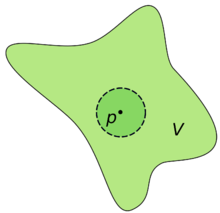
 是 X 中与 S 的距离小于 r 的所有点的集合(或等价的说
是 X 中与 S 的距离小于 r 的所有点的集合(或等价的说 
 的梯度记为:
的梯度记为: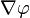 或
或 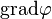
 (nabla)表示矢量微分算子。
(nabla)表示矢量微分算子。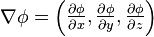
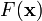 在点
在点 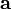 处可微且有定义,那么函数
处可微且有定义,那么函数  下降最快。
下降最快。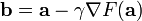
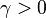 为一个够小数值时成立,那么
为一个够小数值时成立,那么 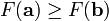 。
。 的局部极小值的初始估计
的局部极小值的初始估计  出发,并考虑如下序列
出发,并考虑如下序列 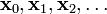 使得
使得
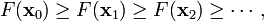
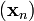 收敛到期望的极值。注意每次迭代步长
收敛到期望的极值。注意每次迭代步长 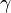 可以改变。
可以改变。


相关推荐
在机器学习领域,梯度下降算法是一种非常基础且重要的优化方法,主要用于求解函数的最小值,尤其是在训练神经网络和构建各种预测模型时。本文将深入探讨梯度下降的原理、实现过程以及它在实际应用中的重要性。 一、...
梯度下降算法是一种在机器学习和优化问题中广泛使用的迭代方法,用于求解函数的局部最小值。在本示例中,我们关注的是如何在MATLAB环境中实现这一算法。MATLAB是一款强大的数学计算软件,适合进行数值分析和算法开发...
在机器学习领域,梯度下降法是优化模型参数的核心算法之一,它被广泛应用于各种监督学习模型的训练过程。本文将深入探讨两种主要的梯度下降法:批梯度下降(Batch Gradient Descent)和随机梯度下降(Stochastic ...
与传统的梯度下降法相比,随机梯度下降每次迭代只使用一个样本来更新权重,而不是整个数据集的平均梯度,这大大减少了计算成本。 `test.m` 文件很可能是测试随机梯度下降算法的脚本,它会调用 `SGD.m` 文件中的函数...
相比于传统的梯度下降法,SGD每次迭代只用到一个样本来更新模型参数,因此计算速度快且能够避免局部最优,特别是在大数据集上表现优秀。然而,SGD可能会导致模型震荡,使得训练过程不稳定,因此通常需要设置合适的...
梯度下降法是一种在优化问题中广泛使用的数值方法,尤其在机器学习和深度学习领域,它是求解损失函数最小化的主要算法之一。本篇将详细解释梯度下降法的原理、步骤以及如何在MATLAB中实现它。 **一、梯度下降法原理...
梯度下降算法是一种在机器学习和优化问题中广泛使用的迭代方法,主要用于求解函数的局部最小值。在本文中,我们将深入探讨梯度下降的概念、原理,并通过MATLAB实现进行详细解释。 首先,理解梯度的基本概念至关重要...
4. **科研数据分析**:在数据分析中,梯度下降可以帮助我们找到最佳拟合模型,比如在回归分析中,通过梯度下降法调整模型参数,使得预测误差最小化。MATLAB的统计和机器学习工具箱包含了许多预定义的模型,但自定义...
描述中提到的博客《逻辑与思考系列[1/300]: 梯度下降法及matlab实践》可能详细介绍了如何利用MATLAB来实现梯度下降算法。通常,该博客可能会涵盖以下内容: 1. **梯度计算**:解释如何在MATLAB中计算目标函数的梯度...
综上所述,本文通过深入解析线性回归的定义、单变量和多变量线性回归的基本原理,以及梯度下降法的理论基础和Matlab实现步骤,展示了如何在Matlab环境下运用梯度下降算法来实现线性回归模型。此外,通过梯度下降法的...
在本项目中,"梯度下降法VS2008_C++" 提供了一个使用C++编程语言在Visual Studio 2008环境下实现梯度下降算法的实例。通过这个项目,我们可以深入理解梯度下降法的原理及其在C++中的实现。 梯度下降法的基本思想是...
损失使用平方函数,简单的线性模型 y = theta1 + theta2 * x
梯度下降算法有多种变种,包括批量梯度下降算法(Batch Gradient Descent)、随机梯度下降算法(Stochastic Gradient Descent)和小批量梯度下降算法(Mini-batch Gradient Descent)。 批量梯度下降算法是指使用...
c#实现梯度下降算法逻辑回归c#实现梯度下降算法逻辑回归c#实现梯度下降算法逻辑回归
梯度下降算法是一种在机器学习和优化问题中广泛使用的迭代方法,主要用于求解函数的局部最小值。在本文中,我们将深入探讨梯度下降的基本概念、工作原理、数学基础,以及如何通过Matlab实现它。 一、梯度下降概述 ...
梯度下降法是一种在优化问题中广泛使用的迭代算法,尤其在机器学习和深度学习领域,用于寻找函数最小值。它的核心思想是沿着目标函数梯度的反方向不断更新参数,以逐步接近局部或全局最小值。以下是梯度下降法的详细...
梯度下降详解 梯度下降是一种常用的机器学习算法,用于寻找函数的最小值,以解决回归问题。下面是对梯度下降算法的详细讲解,包括原理讲解、算法实例和简单代码示例。 原理讲解 梯度下降算法的原理是通过迭代更新...
kNN(K-最近邻)算法与梯度下降算法是机器学习领域中两种重要的方法,它们各自在不同的问题上发挥着关键作用。 首先,我们来深入理解kNN算法。kNN是一种非参数监督学习方法,主要用于分类任务。其基本思想是,给定...
标题中的“path_smoother-master_基于梯度下降法的弯道路径优化_”表明我们关注的是一个关于路径平滑优化的项目,它特别针对弯道场景,利用了梯度下降算法来改善路径的质量。这个项目可能是一个开源库或代码实现,...