在一元函数中,我们已经知道导数就是函数的变化 率。对于二元函数我们同样要研究它的“变化率”。然
而,由于自变量多了一个,情况就要复杂的多。
一、几何意义
在xOy平面内,当动点由P(x0,y0)沿不同方向变化时,函数f(x,y)的变化快慢一般说来是不同的,因此就需要研究f(x,y)在(x0,y0)点处沿不同方向的变化率。
偏导数表示固定面上一点的切线斜率
假设ƒ是一个多元函数。例如:
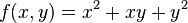 。
。
我们希望求出函数在点(1, 1, 3)的对x的偏导数;对应的切线与xOz平面平行。
因为曲面上的每一点都有无穷多条切线,描述这种函数的导数相当困难。偏导数就是选择其中一条切线,并求出它的斜率。通常,最感兴趣的是垂直于y轴(平行于xOz平面)的切线,以及垂直于x轴(平行于yOz平面)的切线。
一种求出这些切线的好办法是把其他变量视为常数。例如,欲求出以上的函数在点(1, 1, 3)的与xOz平面平行的切线,我们把变量y视为常数。右图中显示了函数的图像以及这个平面。左图中显示了函数在平面y = 1上是什么样的。通过求出这个图中的切线,我们发现ƒ在点(1, 1, 3)的与xOz平面平行的切线的斜率是3。我们把它记为:
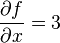
在点(1, 1, 3),或称“f在(1, 1, 3)的关于x的偏导数是3”。
二、定义
在这里我们只学习函数f(x,y)沿着平行于x轴和平行于y轴两个特殊方位变动时,f(x,y)的变化率。
偏导数的算子符号为:∂
偏导数反映的是函数沿坐标轴正方向的变化率。

x方向的偏导
设有二元函数z=f(x,y),点(x0,y0)是其定义域D内一点.把y固定在y0而让x在x0有增量△x,相应地函数z=f(x,y)有增量(称为对x的偏增量)△z=f(x0+△x,y0)-f(x0,y0)。
如果△z与△x之比当△x→0时的极限存在,那么此极限值称为函数z=f(x,y)在(x0,y0)处对x的偏导数(partial derivative)。记作f'x(x0,y0)。
y方向的偏导
函数z=f(x,y)在(x0,y0)处对x的偏导数,实际上就是把y固定在y0看成常数后,一元函数z=f(x,y0)在x0处的导数
同样,把x固定在x0,让y有增量△y,如果极限存在 那么此极限称为函数z=(x,y)在(x0,y0)处对y的偏导数。记作f'y(x0,y0)
三、高阶偏导数
如果二元函数z=f(x,y)的偏导数f'x(x,y)与f'y(x,y)仍然可导,那么这两个偏导函数的偏导数称为z=f(x,y)的二阶偏导数。 二元函数的二阶偏导数有四个:f"xx,f"xy,f"yx,f"yy.
注意:f"xy与f"yx的区别在于:前者是先对x求偏导,然后将所得的偏导函数再对y求偏导;后者是先对y求偏导再对x求偏导.当f"xy与f"yx都连续时,求导的结果与先后次序无关。
分享到:












![deepfuture的博客: 深未来(深度创造未来)[deepfuture@yeah.net] deepfuture的博客](https://www.iteye.com/upload/logo/user/690059/d08c7f3a-9298-3a06-9235-0d0226833f0a.jpg?1717538039)

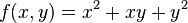 。
。

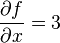




相关推荐
"高等数学偏导数PPT学习教案" 本资源摘要信息是根据同济大学高等数学上D偏导数...本资源摘要信息提供了偏导数的定义、几何意义、计算法、应用和证明等方面的知识点,以帮助学习者更好地理解和掌握偏导数的概念和应用。
偏导数的几何意义是,对于二维函数,一阶偏导数对应着函数图像在某点切线的斜率。例如,\(\frac{\partial f}{\partial x}\)表示曲线在点M0处沿x轴方向的切线斜率,而\(\frac{\partial f}{\partial y}\)表示沿y轴方向...
二、偏导数的几何意义及函数偏导数存在与函数连续的关系 偏导数的几何意义是在二维平面上,函数关于x或y的切线斜率。如果函数f在某点的偏导数存在,那么在该点沿着对应坐标轴的方向有明确的切线斜率。函数在某点的偏...
此外,偏导数的几何意义在于,它可以用切平面来理解,即在多变量函数图形上的某一点,偏导数描述了在该点处的一个主要方向的变化率。而高阶偏导数则是对偏导数进行再次求导,它们在描述函数的局部性质时提供了更为...
本文将对偏导数的概念、计算方法、几何意义和高阶偏导数进行详细的介绍。 一、 偏导数概念及其计算 偏导数是指函数在某一点处对某个自变量的变化率。例如,函数 z = f(x, y) 在点 (x0, y0) 处的偏导数可以定义为:...
偏导数的几何意义是曲面被平面所截得的曲线在点处的切线的斜率。例如,函数 $z = f(x, y)$ 在点 $(x_0, y_0)$ 处对 $x$ 的偏导数 $\frac{\partial z}{\partial x}$ 是曲面被平面 $y = y_0$ 所截得的曲线在点 $(x_0, ...
《一偏导数的定义及其计算法》 偏导数是多元函数微积分中的核心概念,它是用来描述函数在多维空间中沿着某一特定方向的变化率。偏导数的定义和计算方法对于理解和掌握多元函数的性质至关重要。 首先,我们定义函数...
根据提供的文件信息,我们可以归纳出以下关键知识点,主要围绕着偏导...理解偏导数的定义及其几何意义有助于我们更好地理解和应用这一概念。此外,掌握基本的偏导数计算方法和相关的性质定理对于解决实际问题非常重要。
高等数学是数学的基础课程之一,尤其对于理工科的学生而言至关重要。第八章的第二节主要讨论了偏导数这一概念,它是...通过深入理解和熟练掌握偏导数的计算方法及几何意义,我们可以更好地理解和应用多元函数微积分。
在本讲义中,我们将深入探讨二元函数的可微性及其相关的偏导数概念。 首先,我们来看可微性。一个函数在某点可微,意味着它可以被该点附近的一条直线近似,这条直线的斜率由函数在该点的切线决定。具体来说,如果...
本资源摘要信息涵盖了高数下册的主要内容,包括空间分析、向量代数、直线、曲线、曲面、多元函数微分法及其运用、偏导数、隐函数微分法、二元复合函数的偏(全)导数、偏导数的几何应用、极值、条件极值和重积分等。...
扩展的伽玛函数、广义伽玛函数以及不完全伽玛函数的偏导数在数学分析中具有重要的意义,并且在实际应用中也有着广泛的作用。比如,伽马分布的概率密度函数可以表示为: f(x; k, θ) = (x^(k-1) e^(-x/θ)) / (θ^k ...
3. 极值点的判定通常基于偏导数,包括一阶偏导数和二阶偏导数,题目中包含的计算题会要求学生找出函数的局部极值。 **计算题部分** 计算题涵盖了平面和空间直线、平面的方程求解,直线与平面的夹角计算,点到平面...
向量函数导数的几何意义是曲线在某点的切向量,其方向表示参数增加的方向,长度表示曲线在该点的切线斜率。例如,曲线F(t) = (f1(t), f2(t), f3(t))在点(t0, F(t0))的切向量为(F'(t0), f'(t0), f''(t0)),其中f'表示...
偏导数的几何意义在于它描述了在某一给定点,函数沿坐标轴方向的变化趋势,即切线斜率。混合偏导数的性质强调了在一定条件下,偏导数的求导顺序可以互换,这为计算提供了便利。在实际的习题解答中,学生通过各种实际...
理解偏导数的定义和几何意义,以及它与连续性的关系。掌握求偏导数的规则和公式,与一元函数求导类似。 2. 高阶偏导数:理解高阶偏导数的概念,注意记号和求导顺序。当二元函数有二阶连续偏导数时,求导顺序无关。 3...
1. 偏导数:理解偏导数的定义,例如对二元函数求x和y方向的偏导数,并了解它们的几何意义和与连续性的关系。 2. 高阶偏导数:求解更高阶的偏导数,注意符号和求导顺序。 3. 全微分:如果函数的改变量可以表示为偏导...
3. 多元函数的连续性:与一元函数的连续性类似,但扩展到多变量的情况,探讨函数在某区域的连续性及其几何意义。 4. 偏导数:学习如何对多变量函数求偏导,理解偏导数的几何意义和物理意义。 5. 复合函数的偏导数...
- **偏导数的几何意义**:偏导数可以解释为曲面上的切线斜率,如∂f/∂x对应于曲面在平面y = y0上的切线对x轴的斜率。 - **偏导数的存在与连续性**:在一元函数中,可导性意味着连续,但在多元函数中,偏导数存在...
这部分将讲解如何计算一个函数对某个自变量的偏导数,以及如何理解偏导数的几何意义。 3. **6.3 全微分**: 全微分是函数在某一点的微小变化,是所有偏导数的线性组合。这部分将讨论全微分的存在性和可微性条件,...