转 http://www.cnblogs.com/soroman/archive/2008/03/24/1118996.html
关于万向节死锁(Gimbal Lock)
以前发过一篇文章http://www.cnblogs.com/soroman/archive/2006/10/11/526163.html
是关于万向节死锁(Gimbal Lock)的,里面翻译了2
维坐标系中的万向节死锁问题的阐述。后来,参考了各位bloger的观点以及一些资料,整理了一下3维下的Gimbal Lock问题,算是加深一下理解吧,如下:
在3维中常用的欧拉角坐标定向系统是用绕三个轴旋转的角度来表示物体的朝向(Rx,Ry,Rz)(注意三个轴是针对物体坐标系的)。如图1,物体处于世界坐标系(Xw,Yw,Zw)原点,此时物体坐标系(Xl,Yl,Zl)和世界坐标系重合(
这里我使用右手坐标系。
你也可以使用左手坐标系,无所谓,一样
)。此时,规定物体的朝向为(0,0,0)。
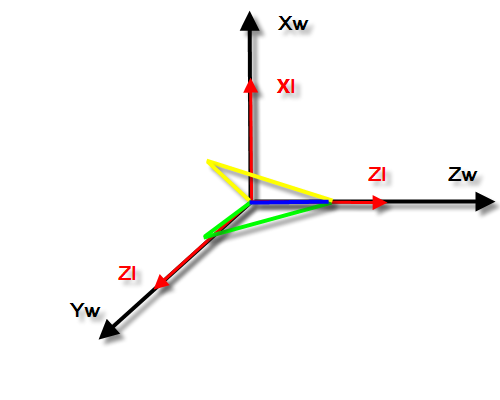
图1:物体的初始朝向
现在开始旋转物体,先绕物体坐标系x轴(Xl)旋转30度(这里我规定沿着轴向轴的负方向看去,顺时针旋转为正。
你也可以自己规定,无所谓,遵守规定即可),注意,此时的物体坐标系已经发生变化,见图2,
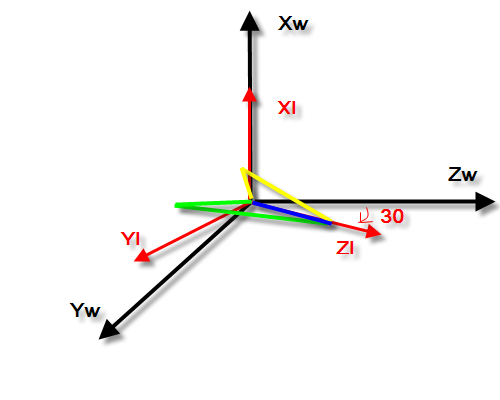
图2:物体绕物体坐标系x轴(Xl)旋转30度
然后再绕Yl轴旋转90度,此时,你会发现Zl轴已经和了世界坐标系X轴共轴。见图3。
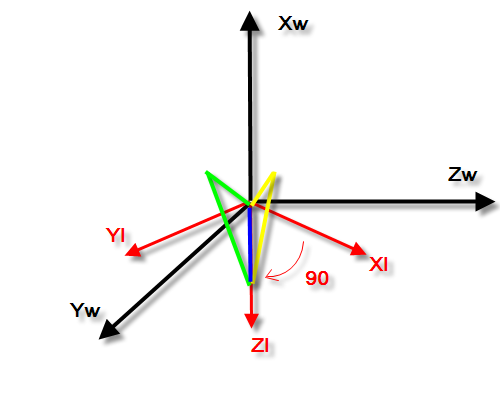
图3:物体绕物体坐标系y轴(Yl)旋转90度
好了,此时使用欧拉角来表示当前物体的方向的话,其坐标应该是(30,90,0),对应旋转顺序是
Xl->Yl->Zl。然而,有意思的是如果再继续旋转,现在按照Zl旋转-40度,发现什么了?咦,怎么感觉已经绕过这个轴旋转过一次了,
虽然轴向相反?^_^,anyway,最后的坐标应该是(30,90,-40),见图4。
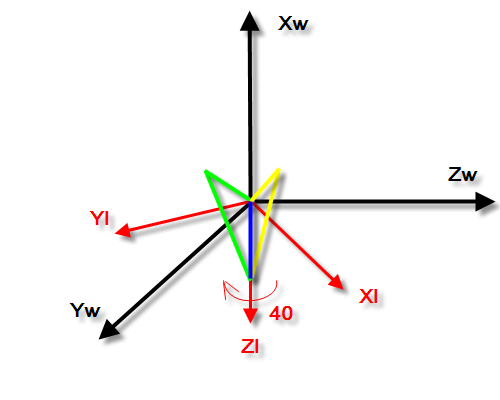
图4:物体绕物体坐标系z轴(Zl)旋转-40度
好了,回到刚才的疑惑上,既然感觉两次旋转是绕同一轴,如果我一开始考虑全部绕该轴的旋转呢?即先绕
Xl旋转30-(-40)=70度,然后再绕Yl旋转90度。^_^怎么样,已经到达和上次旋转的效果了吧。这说明什么?欧拉角坐标
(30,90,-40)和(30-(-40),90,0)等同。甚至坐标(Rx1,90,Rz1)和(Rx2,90,Rz2)相同,只需满足Rx1-
Rz1=Rx2-Rz2。当Rx1-Rz1=Rx2时,Rz2==0,即在这种情况下任何再绕Zl轴的旋转,都可以使用先绕Xl轴来做到。或者从另一个角
度来说,物体现在本质上只能绕两个轴的旋转!即少了一个旋转自由度!这就是3维中的万向节死锁现象。
概括起来可以这么说,绕着物体坐标系中某一个轴,比如y轴的+(-)90度的某次旋转,使得这次旋转的
前一次绕物体坐标系x轴的旋转和这次旋转的后一次绕物体坐标系z轴的旋转的两个旋转轴是一样(一样的意思是指在世界坐标系中,两次旋转轴是共轴的但方向相
反),从而造成一个旋转自由度丢失。
实际上,使用3个量来表示3维空间的朝向的系统都会遭遇这个问题,除非用4个量来表示,如四元数。
2维的情况下欧拉角系统的万向节死锁导致了望远镜不能跟踪飞行器的位置,用某人的话就是在某种坐标系统下,空间中连续的的位置,不能用连续的坐标值来表示
。看看3维情况下是不是也是这样?是不是不能跟踪飞行器的朝向?
举例:飞行器开始的方向是如图1所示,对应欧拉角坐标(0,0,0)。现在飞行器按照绕Xl 30度,然后绕Yl 40度,最后绕Zl 50度的顺序旋转,对应地,欧拉角坐标来跟踪的话是(30,40,50)。最后飞行器的朝向是如图5所示。
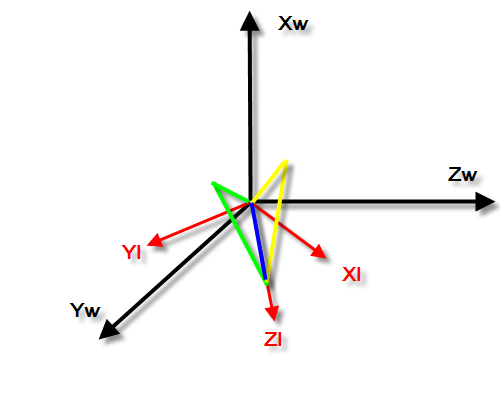
图5:坐标(30,40,50)对应的朝向
现在,飞行器又开始绕Xl轴转个1度。那么现在,欧拉坐标相应地变成(31,40,50)来跟踪,这个坐标对应的飞行器的朝向对吗?实际上是对的,没有问题,一切OK。
换个情况,飞行器从图1初始位置按照绕Xl 30度,然后绕Yl 90度,最后绕Zl
-40度的顺序旋转,对应地,欧拉角坐标来跟踪的话是(30,90,-40),最后飞行器的朝向是如图4所示。现在,飞行器又开始绕Xl轴转个1度。那么
现在,欧拉坐标相应地变成(31,90,-40)来跟踪,对吗?比划看看,使用这个坐标,飞行器肯定对不上了!万向节死锁还是那么讨厌。
这也是为什么3维的情况下,欧拉角插值不适合用来表示旋转插值(等角速度)的原因。使用四元数插值吧,可以参考:http://www.cnblogs.com/soroman/archive/2006/09/19/509597.html
分享到:














相关推荐
万向节死锁(Gimbal Lock)是三维计算机图形学和机器人学中经常遇到的一个问题。其名称源于使用万向节(Gimbal)——一种可以围绕三个正交轴旋转的机械装置——来模拟三维空间中的物体旋转时发生的现象。在计算机...
旋转时 Gimbal Lock(通常译为万向锁或者万向节死锁)的产生原因.虽然 这方面的资料很多,但是某些解释可能会让人比较费解(比如 Wikipedia 上那个球型 Gimbal 的动画) ,有时候直接从数学上来理解反而会更直观一 点.和...
在提供的压缩包文件"**GimbalLock-master**"中,可能包含了Unity3D项目,演示了万向节锁定的现象以及如何使用上述策略来解决。通过运行和分析这个项目,你可以更直观地理解万向节锁定,并学习如何在实际开发中避免它...
- **万向节死锁(Gimbal Lock)**是欧拉角描述法的一个主要问题。当两个旋转轴对齐时,就会发生万向节死锁,导致一个自由度丢失。 #### 欧拉角与Yaw、Pitch、Roll的区别 尽管欧拉角和Yaw、Pitch、Roll都涉及沿三个...
这种方法简单直观,但存在万向节死锁(Gimbal Lock)问题,当两个或更多旋转轴重合时,会导致姿态表示的丢失。 "oulajiao.m" 文件可能包含了以下关键部分: 1. **欧拉角到旋转矩阵的转换**:这通常通过计算旋转...
欧拉角通常以三个轴的角度来描述物体的旋转,而四元数则是一种更高效且避免了万向节死锁(Gimbal Lock)问题的表示方法。下面将详细解释两者之间的转换以及C语言实现的相关知识点。 1. **欧拉角**:欧拉角由三个...
矩阵乘法可以组合多个旋转,但存在万向节死锁(Gimbal Lock)问题,当沿着特定顺序连续进行两个或更多个90度旋转时,会丢失一个自由度。 2. **欧拉角**:欧拉角是一种更直观的方式来描述3D旋转,它由三个旋转角度...
但欧拉角有其固有的缺陷,例如当使用三个独立的旋转来描述旋转时,可能会出现万向节死锁(Gimbal Lock)。这意味着在某些特定的旋转角度上,两个旋转轴重合,使得无法区分绕该轴的旋转与其他轴的旋转。 四元数是一...
相对于欧拉角,四元数避免了万向节死锁(Gimbal Lock)问题,更适合于连续的角度变化计算。在飞行器、机器人和虚拟现实等领域,四元数常用于表示物体的姿态。 欧拉角是另一种表示三维旋转的方法,通常由三个角度...
欧拉角易于理解和直观,但当存在连续或循环旋转时,可能会出现所谓的万向节死锁(Gimbal Lock)问题,即某些特定条件下,两个或更多轴变得重合,导致旋转精度下降。 为了解决欧拉角的局限性,引入了四元数。四元数...
旋转矩阵是一种二维或三维矩阵,可以表示刚体的旋转,而四元数是扩展复数到四维空间的一种数学工具,对于避免万向节死锁(gimbal lock)问题特别有用。 欧拉角的一个主要问题是万向节死锁,当两个连续的旋转轴重合...
姿态解算中一个重要的概念是GimbalLock(万向节死锁)。万向节死锁发生在使用三个自由度的旋转机构(如万向节)来确定方向时。在特定的旋转配置下,旋转机构会失去一个自由度,导致无法实现某一方向的旋转。以望远镜...
欧拉角直观易懂,但在组合多个旋转时会出现万向节死锁和 gimbal lock 问题。 3. **四元数**:四元数是数学上的一种扩展复数,由实部和三个虚部构成,用于表示三维空间中的旋转。四元数没有万向节死锁问题,计算效率...
与矩阵相比,四元数具有更高效、更简洁的优势,可以避免因矩阵旋转而导致的万向节死锁(Gimbal Lock)问题。本文将深入探讨四元数的概念、如何使用四元数进行旋转,以及它们在OpenGL中的应用。 首先,让我们理解...
- 每个旋转都是相对于前一个旋转后的坐标系进行的,这种累积的旋转特性可能导致所谓的“万向节死锁”(Gimbal Lock)问题,当两个旋转轴对齐时,会导致第三个轴的自由度丢失。 2. **欧拉角到矩阵转换**: - 将...
在MATLAB环境中,四元数的运算和编程可以帮助我们更高效地处理三维旋转问题,避免了欧拉角导致的万向节死锁(Gimbal Lock)现象。 "adjoint.zip_clearv52_matlab_occurkpe_quaternion_四元数编程"这个压缩包文件...
然而,对于旋转操作,传统的方法——欧拉角(yaw, pitch, roll)在处理连续旋转时会出现万向节死锁问题,即 gimbal lock。为了解决这个问题,四元数应运而生。 四元数是一种扩展的复数,由实部和三个虚部组成,它...
相比于传统的欧拉角或旋转矩阵,四元数避免了万向节死锁(gimbal lock)问题,提供了更稳定的表现。 在这个名为“buiheng.zip”的压缩包中,我们重点关注的是四元数与PCA(主成分分析)的结合,以及IDW(距离反比...
与欧拉角或旋转矩阵相比,四元数具有诸多优势,如避免万向节死锁(Gimbal Lock)问题,计算效率高,以及占用存储空间小。在刚体定位问题中,理解并熟练运用四元数至关重要。 首先,我们来了解什么是四元数。四元数...
在计算机图形学中,它们被广泛应用于3D物体的旋转表示、动画制作和坐标变换,因为相比传统的欧几里得坐标系统和矩阵运算,四元数具有更高效的计算优势和避免万向节死锁(Gimbal Lock)的问题。 四元数由一个实部...