- ό╡ΠϋπΙ: 280662 όυκ
- όΑπίΙτ:

- όζξϋΘς: ό╡ΟίΞΩ
-

όΨΘύτιίΙΗύ▒╗
ύν╛ίΝ║ύΚΙίζΩ
- όΙΣύγΕϋ╡Εϋχψ ( 0)
- όΙΣύγΕϋχ║ίζδ ( 0)
- όΙΣύγΕώΩχύφΦ ( 0)
ίφαόκμίΙΗύ▒╗
- 2014-06 ( 1)
- 2014-02 ( 2)
- 2013-12 ( 4)
- όδ┤ίνγίφαόκμ...
όεΑόΨ░ϋψΕϋχ║
-
biglinvyΎ╝γ
ώκ╢ώκ╢ώκ╢
ScrollView scrollTo ύγΕϊ╜┐ύΦρ ίΛρύΦ╗όΧΙόηε
ήΑΡόΧ░όΞχύ╗ΥόηΕήΑΣϊ║ΝίΠΚόιΣήΑΒAVLόιΣ
- ίΞγίχλίΙΗύ▒╗Ύ╝γ
- ίΚΞϋ╜οϊ╣ΜώΚ┤(ϋ╜υϋ╜╜)
- androidίφοϊ╣ι
08ί╣┤9όεΙίΖξίφοΎ╝Ν12ί╣┤7όεΙόψΧϊ╕γΎ╝Νύ╗Υόζθϊ║ΗόΙΣίερϋ╜ψϊ╗╢ίφοώβλόΕΚί┐τϊ╕░ίψΝύγΕίνπίφούΦθό┤╗ήΑΓόφνύ│╗ίΙΩόαψίψ╣ίδδί╣┤ϊ╕Υϊ╕γϋψ╛ύρΜίφοϊ╣ιύγΕίδηώκ╛Ύ╝Νύ┤λί╝ΧίΠΓϋπΒΎ╝γhttp://blog.csdn.net/xiaowei_cqu/article/details/7747205
┬ι
ϊ║ΝίΠΚόιΣ
ϊ║ΝίΠΚόιΣόαψόψΠϊ╕ςύ╗ΥύΓ╣όεΑίνγόεΚϊ╕νϊ╕ςίφΡόιΣύγΕόεΚί║ΠόιΣήΑΓώΑγί╕╕ίφΡόιΣύγΕόι╣ϋλτύπ░ϊ╜εέΑεί╖οίφΡόιΣέΑζΎ╝Ιleft subtreeΎ╝ΚίΤΝέΑείΠ│ίφΡόιΣέΑζΎ╝Ιright subtreeΎ╝ΚήΑΓϊ║ΝίΠΚόιΣύγΕόψΠϊ╕ςύ╗ΥύΓ╣ϋΘ│ίνγίΠςόεΚϊ║Νόμ╡ίφΡόιΣ(ϊ╕Ξίφαίερί║οίνπϊ║Ο2ύγΕύ╗ΥύΓ╣)Ύ╝Νϊ║ΝίΠΚόιΣύγΕίφΡόιΣόεΚί╖οίΠ│ϊ╣ΜίΙΗΎ╝Νόυκί║Πϊ╕ΞϋΔ╜ώλιίΑΤήΑΓ

ϊ║ΝίΠΚόιΣόεΚίΘιύΓ╣ώΘΞϋοΒύγΕόΑπϋ┤ρΎ╝γ
- όΑπϋ┤ρ1Ύ╝γίερϊ║ΝίΠΚόιΣύγΕύυυ i ί▒Γϊ╕ΛϋΘ│ίνγόεΚ2i-1 ϊ╕ςύ╗ΥύΓ╣ήΑΓ (iέΚξ1)
- όΑπϋ┤ρ2Ύ╝γό╖▒ί║οϊ╕║ k ύγΕϊ║ΝίΠΚόιΣϊ╕ΛϋΘ│ίνγίΡτ2k-1 ϊ╕ςύ╗ΥύΓ╣Ύ╝ΙkέΚξ1Ύ╝ΚήΑΓ
- όΑπϋ┤ρ3Ύ╝γίψ╣ϊ╗╗ϊ╜Χϊ╕Αόμ╡ϊ║ΝίΠΚόιΣΎ╝ΝϋΜξίχΔίΡτόεΚn0 ϊ╕ςίΠ╢ίφΡύ╗ΥύΓ╣ήΑΒn2 ϊ╕ςί║οϊ╕║ 2 ύγΕύ╗ΥύΓ╣Ύ╝ΝίΙβί┐ΖίφαίερίΖ│ύ│╗ί╝ΠΎ╝γn0 = n2+1ήΑΓ
- όΑπϋ┤ρ4Ύ╝γίΖ╖όεΚ n ϊ╕ςύ╗ΥύΓ╣ύγΕίχΝίΖρϊ║ΝίΠΚόιΣύγΕό╖▒ί║οϊ╕║log2n+1
- όΑπϋ┤ρ5Ύ╝γϋΜξίψ╣ίΡτ n ϊ╕ςύ╗ΥύΓ╣ύγΕίχΝίΖρϊ║ΝίΠΚόιΣϊ╗Οϊ╕ΛίΙ░ϊ╕Μϊ╕Φϊ╗Οί╖οϋΘ│ίΠ│ϋ┐δϋκΝ 1 ϋΘ│ n ύγΕύ╝ΨίΠ╖Ύ╝ΝίΙβίψ╣ίχΝίΖρϊ║ΝίΠΚόιΣϊ╕φϊ╗╗όΕΠϊ╕Αϊ╕ςύ╝ΨίΠ╖ϊ╕║ i ύγΕύ╗ΥύΓ╣Ύ╝γ
(1) ϋΜξ i=1Ύ╝ΝίΙβϋψξύ╗ΥύΓ╣όαψϊ║ΝίΠΚόιΣύγΕόι╣Ύ╝ΝόΩιίΠΝϊ║▓Ύ╝ΝίΡοίΙβΎ╝Νύ╝ΨίΠ╖ϊ╕║i/2ΎΔ╗ ύγΕύ╗ΥύΓ╣ϊ╕║ίΖ╢ίΠΝϊ║▓ύ╗ΥύΓ╣Ύ╝δ
(2) ϋΜξ 2i>nΎ╝ΝίΙβϋψξύ╗ΥύΓ╣όΩιί╖οίφσίφΡΎ╝ΝίΡοίΙβΎ╝Νύ╝ΨίΠ╖ϊ╕║ 2i ύγΕύ╗ΥύΓ╣ϊ╕║ίΖ╢ί╖οίφσίφΡύ╗ΥύΓ╣Ύ╝δ
(3) ϋΜξ 2i+1>nΎ╝ΝίΙβϋψξύ╗ΥύΓ╣όΩιίΠ│ίφσίφΡύ╗ΥύΓ╣Ύ╝ΝίΡοίΙβΎ╝Νύ╝ΨίΠ╖ϊ╕║2i+1 ύγΕύ╗ΥύΓ╣ϊ╕║ίΖ╢ίΠ│ίφσίφΡύ╗ΥύΓ╣ήΑΓ
ώΘΘύΦρώΥ╛ί╝ΠίφαίΓρύ╗ΥόηΕίχηύΟ░ϊ║ΝίΠΚόιΣ
ώΥ╛ί╝ΠίφαίΓρϊ║ΝίΠΚόιΣ

┬ι
1.ώοΨίΖΙόΙΣϊ╗υϋοΒόηΕώΑιίΠψϊ╗ξϋκρύν║ϊ║ΝίΠΚόιΣύγΕϋΛΓύΓ╣ύγΕύ╗ΥόηΕ Binary_node
2.όηΕώΑιύ▒╗ϊ║ΝίΠΚόιΣ Binary_treeΎ╝Νί╣╢ύ╝ΨίΗβίΖ╢ίΘιϊ╕ςίθ║όευύγΕόΙΡίΣαίΘ╜όΧ░Ύ╝γ
Empty()- όμΑόθξόιΣόαψίΡοϊ╕║ύσ║Ύ╝δclear()- ί░ΗόιΣό╕Ζύσ║Ύ╝δsize()- ί╛ΩίΙ░όιΣύγΕίνπί░ΠΎ╝δleaf_count()- ί╛ΩίΙ░ίΠ╢ίφΡόΧ░ύδχΎ╝δheight()- ί╛ΩίΙ░όιΣώταΎ╝δ
ϊ╗ξίΠΛίΘιϊ╕ςώΘΞϋοΒύγΕόΙΡίΣαίΘ╜όΧ░Ύ╝γ
Binary_tree(const Binary_tree<Entry>&original); όΜ╖ϋ┤ζόηΕώΑιόΙΡίΣαίΘ╜όΧ░ Binary_tree &operator=(const Binary_tree<Entry>&original);ώΘΞϋ╜╜ϋ╡ΜίΑ╝όΥΞϊ╜εύυο ~Binary_tree();όηΡόηΕίΘ╜όΧ░
┬ι
3.ίΙΗίΙτύ╝ΨίΗβώΒΞίΟΗύχΩό│ΧύγΕόΙΡίΣαίΘ╜όΧ░
void inorder(void(*visit)(Entry &)); ϊ╕φί║ΠώΒΞίΟΗΎ╝ΙLVRΎ╝Κ void preorder(void(*visit)(Entry &)); ίΚΞί║ΠώΒΞίΟΗΎ╝ΙVLRΎ╝Κ void postorder(void(*visit)(Entry &)); ίΡΟύ╗φώΒΞίΟΗΎ╝ΙLRVΎ╝Κ
ίδιϊ╕║ϊ║ΝίΠΚόιΣύγΕόΑπϋ┤ρΎ╝Νϊ╕ΚύπΞώΒΞίΟΗύχΩό│ΧόΙΣϊ╗υώΔ╜ύΦρώΑΤί╜ΤίχηύΟ░Ύ╝ΝόΚΑϊ╗ξίΙΗίΙτύ╝ΨίΗβίΖ╢ώΑΤί╜ΤίΘ╜όΧ░
void recursive_inorder(Binary_node<Entry>*sub_root,void (*visit)(Entry &)); void recursive_preorder(Binary_node<Entry>*sub_root,void(*visit)(Entry &)); void recursive_postorder(Binary_node<Entry>*sub_root,void(*visit)(Entry &));
┬ι
4.ϊ╜εϊ╕║ϋ╛ΖίΛσΎ╝ΝόΙΣϊ╗υίΗΞύ╝ΨίΗβϊ╕Αϊ╕ςprint_treeύγΕίΘ╜όΧ░Ύ╝ΝύΦρϊ╗ξϊ╗ξόΜυίΠ╖ϋκρύν║ό│Χϋ╛ΥίΘ║
ίΡΝόι╖ϊ╜┐ύΦρώΑΤί╜ΤΎ╝Νύ╝ΨίΗβώΑΤί╜ΤίΘ╜όΧ░void recursive_print(Binary_node<Entry>*sub_root);
ίΘιϊ╕ςώΘΞϋοΒύγΕίΘ╜όΧ░ϊ╗μύιΒίοΓϊ╕ΜΎ╝γ
template<class Entry>
void Binary_tree<Entry>::inorder(void(*visit)(Entry &))
//Post: The tree has been traversed in inorder sequence
//Uses: The function recursive_inorder
{
recursive_inorder(root,visit);
}
template<class Entry>
void Binary_tree<Entry>::recursive_inorder(Binary_node<Entry>*sub_root,void(*visit)(Entry &))
//Pre: sub_root is either NULL or points to a subtree of the Binary_tree
//Post: The subtree has been traversed in inorder sequence
//Uses: The function recursive_inorder recursively
{
if(sub_root!=NULL){
recursive_inorder(sub_root->left,visit);
(*visit)(sub_root->data);
recursive_inorder(sub_root->right,visit);
}
}
template<class Entry>
void Binary_tree<Entry>::preorder(void(*visit)(Entry &))
//Post: The tree has been traversed in preorder sequence
//Uses: The function recursive_preorder
{
recursive_preorder(root,visit);
}
template<class Entry>
void Binary_tree<Entry>::recursive_preorder(Binary_node<Entry>*sub_root,void(*visit)(Entry &))
//Pre: sub_root is either NULL or points to a subtree of the Binary_tree
//Post: The subtree has been traversed in preorder sequence
//Uses: The function recursive_preorder recursively
{
if(sub_root!=NULL){
(*visit)(sub_root->data);
recursive_preorder(sub_root->left,visit);
recursive_preorder(sub_root->right,visit);
}
}
template<class Entry>
void Binary_tree<Entry>::postorder(void(*visit)(Entry &))
//Post: The tree has been traversed in postorder sequence
//Uses: The function recursive_postorder
{
recursive_postorder(root,visit);
}
template<class Entry>
void Binary_tree<Entry>::recursive_postorder(Binary_node<Entry>*sub_root,void(*visit)(Entry &))
//Pre: sub_root is either NULL or points to a subtree fo the Binary_tree
//Post: The subtree has been traversed in postorder sequence
//Uses: The function recursive_postorder recursively
{
if(sub_root!=NULL){
recursive_postorder(sub_root->left,visit);
recursive_postorder(sub_root->right,visit);
(*visit)(sub_root->data);
}
}
template<class Entry>
void Binary_tree<Entry>::print_tree()
{
recursive_print(root);
cout<<endl;
}
template<class Entry>
void Binary_tree<Entry>::recursive_print(Binary_node<Entry>*sub_root)
{
if(sub_root!=NULL){
cout<<sub_root->data;
cout<<"(";
recursive_print(sub_root->left);
cout<<",";
recursive_print(sub_root->right);
cout<<")";
}
}
//ίΖ╢ϊ╗ΨίΘ╜όΧ░ϋπΒό║ΡύιΒ
ύρΜί║Πύ╗Υόηε
όΠΤίΖξϊ║ΝίΠΚόιΣί╣╢ίχηύΟ░ϊ╕φί║ΠήΑΒίΚΞί║ΠίΤΝίΡΟί║ΠώΒΞίΟΗ
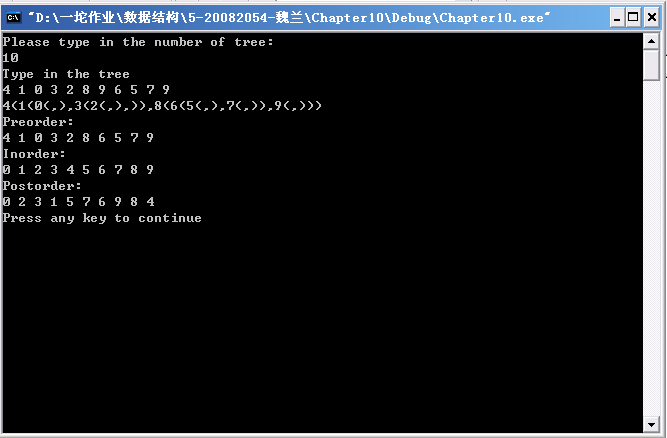
┬ι
AVLόιΣ
AVLόιΣί╛ΩίΡΞϊ║ΟίΖ╢ίΠΣόαΟϋΑΖG.M.Adelson-VelskyίΤΝE.M.LandisήΑΓAVLόιΣόαψϊ╕Αϊ╕ςίΡΕύ╗ΥύΓ╣ίΖ╖όεΚί╣│ϋκκώταί║ούγΕόΚσί▒ΧύγΕϊ║ΝίΠΚόΡεύ┤λόιΣήΑΓίερAVLόιΣϊ╕φΎ╝Νϊ╗╗ϊ╕Αύ╗ΥύΓ╣ύγΕϊ╕νϊ╕ςίφΡόιΣύγΕώταί║οί╖χόεΑίνγϊ╕║1Ύ╝ΝAVLόιΣύγΕώταί║οϊ╕Ξϊ╝γϋ╢Ζϋ┐Θ1Ύ╝ΝAVLόιΣόΩλόεΚϊ║ΝίΠΚόΡεύ┤λόιΣύγΕόΡεύ┤λόΧΙύΟΘίΠΙίΠψϊ╗ξώΒ┐ίΖΞϊ║ΝίΠΚόΡεύ┤λόιΣύγΕόεΑίζΠόΔΖίΗ╡Ύ╝ΙώΑΑίΝΨόιΣΎ╝ΚίΘ║ύΟ░ήΑΓ
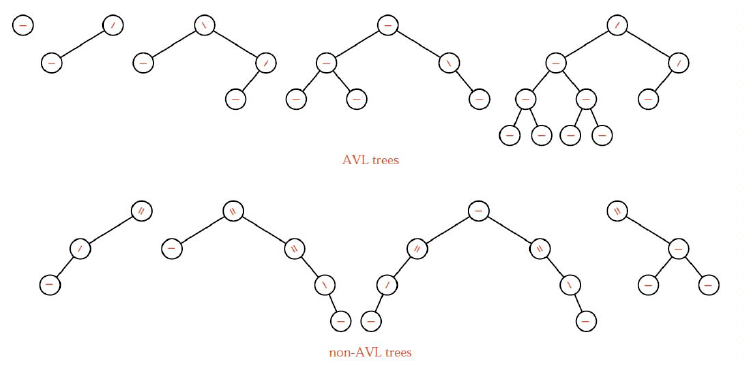
AVLόιΣύγΕϋκρύν║ϊ╕Οϊ║ΝίΠΚόΡεύ┤λόιΣύ▒╗ϊ╝╝Ύ╝ΝίΖ╢όΥΞϊ╜είθ║όευύδ╕ίΡΝΎ╝Νϊ╜ΗόΠΤίΖξίΤΝίΙιώβνόΨ╣ό│ΧώβνίνΨΎ╝Νίδιϊ╕║ίχΔϊ╗υί┐Ζώκ╗ϊ╕ΞόΨφύδΣόΟπύ╗ΥύΓ╣ύγΕί╖οίΠ│ίφΡόιΣύγΕύδ╕ίψ╣ώταί║οΎ╝Νϋ┐βϊ╣θόφμόαψAVLόιΣύγΕϊ╝αίΛ┐όΚΑίερήΑΓ
ίχηύΟ░AVLόιΣύγΕύδ╕ίΖ│ϋ┐ΡύχΩ
1ήΑΒώοΨίΖΙόΙΣϊ╗υϊ┐χόΦ╣ύ╗ΥόηΕBinary_nodeΎ╝ΝίληίΛιBalance_factorύΦρϊ╗ξϋκρύν║ϋΛΓύΓ╣ί╣│ϋκκόΔΖίΗ╡
2ήΑΒϊ╗Οϊ║ΝίΠΚόΡεύ┤λόιΣϊ╕φό┤╛ύΦθίΘ║AVLόιΣΎ╝Νύ╝ΨίΗβίΖ╢ίΖ│ώΦχύγΕόΠΤίΖξίΤΝίΙιώβνόΙΡίΣαίΘ╜όΧ░ήΑΓ
Error_code insert(const Record &new_data); Error_code remove(const Record &old_data);
3ήΑΒίΖξίΤΝίΙιώβνίΘ╜όΧ░όΙΣϊ╗υώΔ╜ύΦρώΑΤί╜ΤίχηύΟ░
ύ╝ΨίΗβώΑΤί╜ΤίΘ╜όΧ░Ύ╝γ
Error_code avl_insert(Binary_node<Record>* &sub_root,
const Record &new_data,bool &taller);
Error_code avl_remove(Binary_node<Record>* &sub_root,
const Record &target,bool &shorter);
ϊ╗ξίΠΛίΘιϊ╕ςώΘΞϋοΒύγΕϋ░ΔύΦρίΘ╜όΧ░Ύ╝γ
ί╖οόΩΜίΠ│όΩΜίΘ╜όΧ░Ύ╝γ
void rotate_left(Binary_node<Record>* &sub_root); void rotate_right(Binary_node<Record>* &sub_root);
ϊ╕νόυκόΩΜϋ╜υύγΕί╖οίΠ│ί╣│ϋκκίΘ╜όΧ░
void right_balance(Binary_node<Record>* &sub_root); void left_balance(Binary_node<Record>* &sub_root);
ίΙιώβνίΘ╜όΧ░ϋ┐αϋοΒίΙΗίΙτύ╝ΨίΗβίΙιώβνί╖οόιΣίΤΝίΙιώβνίΠ│όιΣύγΕώΑΤί╜ΤίΘ╜όΧ░
Error_code avl_remove_right(Binary_node<Record>&sub_root,
const Record &target,bool &shorter);
Error_code avl_remove_left(Binary_node<Record>*&sub_root,
const Record &target,bool &shorter);
┬ι
4ήΑΒϊ╕ςώΘΞϋοΒύγΕόΙΡίΣαίΘ╜όΧ░ϊ╗μύιΒίοΓϊ╕ΜΎ╝γ
template<class Record>
Error_code AVL_tree<Record>::insert(const Record &new_data)
//Post: If the key of new_data is already in the AVL_tree, a code of duplicate_error
// is returned. Otherwise, a code of success is returned and the Record
// new_data is inserted into the tree in such a way that the properties of an
// AVL tree are preserved.
{
bool taller;
return avl_insert(root,new_data,taller);
}
template<class Record>
Error_code AVL_tree<Record>::avl_insert(Binary_node<Record>* &sub_root, const Record &new_data,bool &taller)
//Pre: sub_root is either NULL or points to a subtree of the AVL tree
//Post: If the key of new_data is already in the subtree, a code of duplicate_error
// is returned. Otherwise, a code of success is returned and the Record
// new_data is inserted into the subtree in such a way that the properties of
// an AVL tree have been preserved. If the subtree is increase in height, the
// parameter taller is set to true; otherwise it is set to false
//Uses: Methods of struct AVL_node; functions avl_insert recursively, left_balance, and right_balance
{
Error_code result=success;
if(sub_root==NULL){
sub_root=new Binary_node<Record>(new_data);
taller=true;
}
else if(new_data==sub_root->data){
result=duplicate_error;
taller=false;
}
else if(new_data<sub_root->data){//Insert in left subtree
result=avl_insert(sub_root->left,new_data,taller);
if(taller==true)
switch(sub_root->get_balance()){//Change balance factors
case left_higher:
left_balance(sub_root);
taller=false;
break;
case equal_height:
sub_root->set_balance(left_higher);
break;
case right_higher:
sub_root->set_balance(equal_height);
taller=false;
break;
}
}
else{ //Insert in right subtree
result=avl_insert(sub_root->right,new_data,taller);
if(taller==true)
switch(sub_root->get_balance()){
case left_higher:
sub_root->set_balance(equal_height);
taller=false;
break;
case equal_height:
sub_root->set_balance(right_higher);
break;
case right_higher:
right_balance(sub_root);
taller=false; //Rebalancing always shortens the tree
break;
}
}
return result;
}
template<class Record>
void AVL_tree<Record>::right_balance(Binary_node<Record>* &sub_root)
//Pre: sub_root points to a subtree of an AVL_tree that is doubly unbalanced
// on the right
//Post: The AVL properties have been restored to the subtree
{
Binary_node<Record>* &right_tree=sub_root->right;
switch(right_tree->get_balance()){
case right_higher:
sub_root->set_balance(equal_height);
right_tree->set_balance(equal_height);
rotate_left(sub_root);
break;
case equal_height:
cout<<"WARNING: program error detected in right_balance "<<endl;
case left_higher:
Binary_node<Record>*sub_tree=right_tree->left;
switch(sub_tree->get_balance()){
case equal_height:
sub_root->set_balance(equal_height);
right_tree->set_balance(equal_height);
break;
case left_higher:
sub_root->set_balance(equal_height);
right_tree->set_balance(right_higher);
case right_higher:
sub_root->set_balance(left_higher);
right_tree->set_balance(equal_height);
break;
}
sub_tree->set_balance(equal_height);
rotate_right(right_tree);
rotate_left(sub_root);
break;
}
}
template<class Record>
void AVL_tree<Record>::left_balance(Binary_node<Record>* &sub_root)
{
Binary_node<Record>* &left_tree=sub_root->left;
switch(left_tree->get_balance()){
case left_higher:
sub_root->set_balance(equal_height);
left_tree->set_balance(equal_height);
rotate_right(sub_root);
break;
case equal_height:
cout<<"WARNING: program error detected in left_balance"<<endl;
case right_higher:
Binary_node<Record>*sub_tree=left_tree->right;
switch(sub_tree->get_balance()){
case equal_height:
sub_root->set_balance(equal_height);
left_tree->set_balance(equal_height);
break;
case right_higher:
sub_root->set_balance(equal_height);
left_tree->set_balance(left_higher);
break;
case left_higher:
sub_root->set_balance(right_higher);
left_tree->set_balance(equal_height);
break;
}
sub_tree->set_balance(equal_height);
rotate_left(left_tree);
rotate_right(sub_root);
break;
}
}
template<class Record>
void AVL_tree<Record>::rotate_left(Binary_node<Record>* &sub_root)
//Pre: sub_root points to a subtree of the AVL_tree. This subtree has
// a nonempty right subtree.
//Post: sub_root is reset to point to its former right child, and the
// former sub_root node is the left child of the new sub_root node
{
if(sub_root==NULL||sub_root->right==NULL)//impossible cases
cout<<"WARNING: program error detected in rotate_left"<<endl;
else{
Binary_node<Record>*right_tree=sub_root->right;
sub_root->right=right_tree->left;
right_tree->left=sub_root;
sub_root=right_tree;
}
}
template<class Record>
void AVL_tree<Record>::rotate_right(Binary_node<Record>*&sub_root)
{
if(sub_root==NULL||sub_root->left==NULL)
cout<<"WARNING:program error in detected in rotate_right"<<endl;
else{
Binary_node<Record>*left_tree=sub_root->left;
sub_root->left=left_tree->right;
left_tree->right=sub_root;
sub_root=left_tree;
}
}
template<class Record>
Error_code AVL_tree<Record>::remove(const Record &old_data)
{
bool shorter;
return avl_remove(root,old_data,shorter);
}
template<class Record>
Error_code AVL_tree<Record>::avl_remove(Binary_node<Record>* &sub_root,
const Record &target,bool &shorter)
{
Binary_node<Record>*temp;
if(sub_root==NULL)return fail;
else if(target<sub_root->data)
return avl_remove_left(sub_root,target,shorter);
else if(target>sub_root->data)
return avl_remove_right(sub_root,target,shorter);
else if(sub_root->left==NULL){//Found target: delete current node
temp=sub_root; //Move right subtree up to delete node
sub_root=sub_root->right;
delete temp;
shorter=true;
}
else if(sub_root->right==NULL){
temp=sub_root; //Move left subtree up to delete node
sub_root=sub_root->left;
delete temp;
shorter=true;
}
else if(sub_root->get_balance()==left_higher){
//Neither subtree is empty; delete from the taller
temp=sub_root->left;//Find predecessor of target and delete if from left tree
while(temp->right!=NULL)temp=temp->right;
sub_root->data=temp->data;
avl_remove_left(sub_root,temp->data,shorter);
}
else{
temp=sub_root->right;
while(temp->left!=NULL)temp=temp->left;
sub_root->data=temp->data;
avl_remove_right(sub_root,temp->data,shorter);
}
return success;
}
template<class Record>
Error_code AVL_tree<Record>::avl_remove_right(Binary_node<Record>
*&sub_root,const Record &target,bool &shorter)
{
Error_code result=avl_remove(sub_root->right,target,shorter);
if(shorter==true)switch(sub_root->get_balance()){
case equal_height:
sub_root->set_balance(left_higher);
shorter=false;
break;
case right_higher:
sub_root->set_balance(equal_height);
break;
case left_higher:
Binary_node<Record>*temp=sub_root->left;
switch(temp->get_balance()){
case equal_height:
temp->set_balance(right_higher);
rotate_right(sub_root);
shorter=false;
break;
case left_higher:
sub_root->set_balance(equal_height);
temp->set_balance(equal_height);
rotate_right(sub_root);
break;
case right_higher:
Binary_node<Record>*temp_right=temp->right;
switch(temp_right->get_balance()){
case equal_height:
sub_root->set_balance(equal_height);
temp->set_balance(equal_height);
break;
case left_higher:
sub_root->set_balance(right_higher);
temp->set_balance(equal_height);
break;
case right_higher:
sub_root->set_balance(equal_height);
temp->set_balance(left_higher);
break;
}
temp_right->set_balance(equal_height);
rotate_left(sub_root->left);
rotate_right(sub_root);
break;
}
}
return result;
}
template<class Record>
Error_code AVL_tree<Record>::avl_remove_left(Binary_node<Record>
*&sub_root,const Record &target,bool &shorter)
{
Error_code result=avl_remove(sub_root->left,target,shorter);
if(shorter==true)
switch(sub_root->get_balance()){
case equal_height:
sub_root->set_balance(right_higher);
shorter=false;
break;
case left_higher:
sub_root->set_balance(equal_height);
break;
case right_higher:
Binary_node<Record>*temp=sub_root->right;
switch(temp->get_balance()){
case equal_height:
temp->set_balance(left_higher);
rotate_right(sub_root);
shorter=false;
break;
case right_higher:
sub_root->set_balance(equal_height);
temp->set_balance(equal_height);
rotate_left(sub_root);
break;
case left_higher:
Binary_node<Record>*temp_left=temp->left;
switch(temp_left->get_balance()){
case equal_height:
sub_root->set_balance(equal_height);
temp->set_balance(equal_height);
break;
case right_higher:
sub_root->set_balance(left_higher);
temp->set_balance(equal_height);
break;
case left_higher:
sub_root->set_balance(equal_height);
temp->set_balance(right_higher);
break;
}
temp_left->set_balance(equal_height);
rotate_right(sub_root->right);
rotate_left(sub_root);
break;
}
}
return result;
}
ίχηώςΝύ╗Υόηε
ίχηύΟ░ίοΓϊ╕ΜίΛθϋΔ╜Ύ╝γ1Ύ╝ΚύΦ▒{4,9,0,1,8,6,3,5,2,7}ί╗║AVLόιΣBΎ╝Νί╣╢ϊ╗ξόΜυίΠ╖ϋκρύν║ό│Χϋ╛ΥίΘ║Ύ╝δ2Ύ╝ΚίΙιώβνBϊ╕φίΖ│ώΦχίφΩϊ╕║8ίΤΝ2ύγΕύ╗ΥύΓ╣Ύ╝Νϋ╛ΥίΘ║ύ╗ΥόηεήΑΓ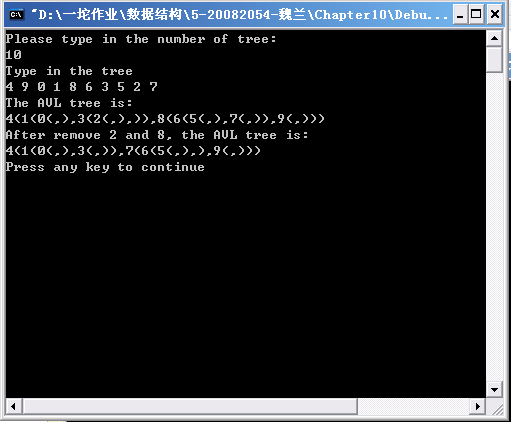
┬ι
ίΙΗόηΡόΑ╗ύ╗Υ
┬ι
ώΘΘύΦρώΥ╛ί╝ΠίφαίΓρύ╗ΥόηΕίχηύΟ░ϊ║ΝίΠΚόιΣ
- ϊ║ΝίΠΚόιΣίερόΠΤίΖξύγΕόΩ╢ίΑβώΑγϋ┐ΘίΙνόΨφί╛ΖόΠΤίΖξόΧ░όΞχϊ╕Οόι╣ϋΛΓύΓ╣όΧ░όΞχύγΕίνπί░ΠΎ╝ΝϋΜξί░Πϊ║Οόι╣όΧ░όΞχΎ╝ΝόΠΤίΖξί╖οόιΣΎ╝ΝίΠΞϊ╣ΜόΠΤίΖξίΠ│όιΣΎ╝ΙόΙΣϊ╗υϋπΕίχγϊ╕Ξϋχ╕όεΚώΘΞίνΞίΖΔύ┤ιΎ╝ΚΎ╝δϊ║ΝίΠΚόιΣύγΕίφαίΓρύ╗ΥόηΕί╕╕ύΦρϊ║ΟόΡεύ┤λύφΚήΑΓϊ╜ΗόΡεύ┤λύγΕόΧΙύΟΘί╕╕ϊ╛ζϋ╡Ψϊ║ΟόιΣύγΕύ╗ΥόηΕήΑΓϋΑΝόιΣύγΕύ╗ΥόηΕϊ╕ΟίΖΔύ┤ιόΠΤίΖξώκ║ί║ΠόεΚί╛ΙίνπίΖ│ύ│╗Ύ╝ΝύΦρϊ╕Λϋ┐░όΨ╣ό│ΧόΠΤίΖξόΩ╢ϋΜξόΠΤίΖξύγΕίΖΔύ┤ιόαψόεΚί║ΠύγΕΎ╝ΝίΙβί╛ΩίΙ░ύγΕόιΣϊ╕ΟώαθίΙΩίΘιϊ╣Οό▓κόεΚίΝ║ίΙτΎ╝Νϊ╣θϋ╡╖ϊ╕ΞίΙ░ϊ╝αίΝΨόΡεύ┤λύγΕύδχύγΕήΑΓ
- ϊ║ΝίΠΚόιΣύγΕώΒΞίΟΗύχΩό│ΧόεΑϊ╕║ώΘΞϋοΒύγΕϊ╕ΑύΓ╣όαψώΑΤί╜ΤΎ╝ΝώΑΤί╜Τϊ╜┐όΙΣϊ╗υϊ╕Ξί┐ΖίΖ│ί┐Δϊ║ΟίΖ╖ϊ╜ΥύγΕώΒΞίΟΗόψΠϊ╕ςϋΛΓύΓ╣ύγΕώκ║ί║ΠΎ╝ΝϋΑΝίΠςόαψί░ΗίΖ╢ύεΜίΒγϊ╕Κϊ╕ςώΔρίΙΗΎ╝ΝίΞ│ί╖οίφΡόιΣΎ╝Νόι╣ϋΛΓύΓ╣Ύ╝ΝίΠ│ίφΡόιΣΎ╝ΝίΖ╖ϊ╜ΥίφΡόιΣύγΕώΒΞίΟΗϊ╗Ξόαψϋ░ΔύΦρίΖ╢ώΑΤί╜ΤίΘ╜όΧ░ήΑΓ
3.ίερόΚΥίΞ░όιΣύγΕόΩ╢ίΑβΎ╝ΝόΙΣίΗβύγΕί╣╢ϊ╕ΞίχΝύ╛ΟΎ╝Νίδιϊ╕║ίψ╣ϊ║ΟίΠ╢ίφΡϋΛΓύΓ╣Ύ╝ΝύΡΗόΔ│ί║Φϋψξϊ╕ΞίΗΞόΚΥίΞ░όΜυίΠ╖Ύ╝Νϊ╜ΗόΙΣώΑγϋ┐ΘίΙνόΨφόι╣ϋΛΓύΓ╣ϊ╕Ξϊ╕║ύσ║ϋΑΝϋ░ΔύΦρώΑΤί╜ΤίΘ╜όΧ░Ύ╝ΝίΞ│ίΠςϋοΒϋΛΓύΓ╣όεΚίΖΔύ┤ιί░▒ϊ╝γϋ╛ΥίΘ║Ύ╝ΙΎ╝ΝΎ╝ΚΎ╝Νϋ┐αόαψϋκρϋ╛╛ίΘ║ϊ║ΗόιΣύγΕόΕΠόΑζΎ╝Νϊ╜Ηί╣╢ό▓κόεΚόΔ│ίΙ░όΑΟόι╖ϋ╛╛ίΙ░ύχΑό┤ΒύγΕόΧΙόηεήΑΓ
ίχηύΟ░AVLόιΣύγΕύδ╕ίΖ│ϋ┐ΡύχΩ
- AVLόιΣόψΠόΠΤίΖξΎ╝ΝίΙιώβνϊ╕Αϊ╕ςϋΛΓύΓ╣ί░▒ϊ╝γίΙνόΨφόιΣύγΕώταί║οί╣╢όΦ╣ίΠαύδ╕ί║ΦϋΛΓύΓ╣ύγΕί╣│ϋκκίδιύ┤ιΎ╝ΝόψΠί╜ΥόεΚϋΛΓύΓ╣ϊ╕ΞίΗΞό╗κϋ╢│AVLόιΣύγΕόΑπϋ┤ρΎ╝ΝύτΜίΞ│ώΑγϋ┐ΘόΩΜϋ╜υί╛ΩίΙ░AVLόιΣ
- όΩΜϋ╜υύγΕίΘ╜όΧ░ίΠΛίΖ╢ί╖πίοβήΑΓϋΑΝόΠΤίΖξίΤΝίΙιώβνίΖΔύ┤ιύγΕίΘ╜όΧ░ϋοΒϋΑΔϋβΣύγΕόΔΖίΗ╡ώζηί╕╕ίνγΎ╝Νϊ╕ΑύπΞόΔΖίΗ╡ό▓κόεΚϋΑΔϋβΣίΙ░ί░▒ίΠψϋΔ╜ϋ╛╛ϊ╕ΞίΙ░όΙΣϊ╗υόΔ│ϋοΒύγΕόΧΙόηεΎ╝ΝίΘ╜όΧ░ύγΕύ╝ΨίΗβώεΑϋοΒόηΒίνπύγΕϋΑΡί┐ΔίΤΝίψ╣ύ╝ΨύρΜϋψφίΠξύγΕύΗθύ╗ΔόΟΝόΠκήΑΓί╛Ιίνγίε░όΨ╣όΙΣόαψίΠΓϋΑΔϊ╣οϊ╕ΛύγΕΎ╝ΝίΙτϊ║║ύγΕϊ╗μύιΒόΙΣίΠψϊ╗ξύΡΗϋπμΎ╝Νϊ╜ΗόΙΣϋΘςί╖▒ίΗβίΠψϋΔ╜ϋ┐αόαψϊ╝γό╝ΠόΟΚί╛ΙίνγόΔΖίΗ╡ήΑΓ
ϋ╜υϋ╜╜ϋψ╖ό│ρόαΟίΘ║ίνΕΎ╝γhttp://blog.csdn.net/xiaowei_cqu/article/details/7888562
- 2012-08-21 00:30
- ό╡ΠϋπΙ 1098
- ϋψΕϋχ║(0)
- ίΙΗύ▒╗:ύπ╗ίΛρί╝ΑίΠΣ
- όθξύεΜόδ┤ίνγ
ίΠΣϋκρϋψΕϋχ║
-
unityίθ║ύκΑί╝ΑίΠΣ----ύΚσϊ╜Υϊ╜Ξύπ╗ίΤΝόΩΜϋ╜υίχηύΦρϊ╗μύιΒ
2013-11-21 22:46 1270using UnityEngine; using Syst ... -
android ίΛρόΑΒόΩ╢ώΤθ ώβΕό║ΡύιΒ
2013-09-24 12:03 1281┬ι ┬ι ϋΘςίχγϊ╣ΚViewίχηϋ╖╡ ϊ╛ΜίφΡϊ╗μύιΒ ϋΘςίχγϊ╣ΚίΛρόΑΒόΩ╢ώΤθ ... -
android Dialog ϋΔΝόβψώΩχώλα
2013-08-14 11:22 1206┬ι ┬ι ┬ι ┬ιόΙΣϊ╗υίερϊ╜┐ύΦρϋΘςίχγϊ╣ΚύγΕDialogύγΕόΩ╢ίΑβΎ╝ΝίΨεόυλϋΘςί╖▒ ... -
ScrollView scrollTo ύγΕϊ╜┐ύΦρ ίΛρύΦ╗όΧΙόηε
2013-08-05 17:43 4603┬ι ┬ιϊ╗ΛίνσύΦρίΙ░ϊ║ΗScrollView scrollToόΨ╣ό│Χ ... -
Androidϊ╕φViewύ╗αίΙ╢ϊ╝αίΝΨϊ╣Μϊ╕Α---- ϊ╝αίΝΨί╕Δί▒Αί▒Γόυκ
2012-09-04 23:00 1074┬ι ┬ι ┬ι ... -
Androidϊ╕φViewύ╗αίΙ╢ϊ╝αίΝΨϊ║Νϊ╕Α---- ϊ╜┐ύΦρ<include />όιΘύφ╛ίνΞύΦρί╕Δί▒ΑόΨΘϊ╗╢
2012-09-08 13:54 1055┬ι ... -
Androidϊ╕φViewύ╗αίΙ╢ϊ╝αίΝΨϊ╣Μϊ╕Κ---- ϊ╝αίΝΨView
2012-09-13 21:00 1082┬ι ... -
ίΖ░όηΩϊ╗╗ίΛκύχκύΡΗί║ΦύΦρύρΜί║ΠώδΠί╜λύΚΙϊ╗ξίΠΛόοΓϋοΒϋψ┤όαΟ
2012-09-15 21:54 880... -
Androidϊ╕φmeasureϋ┐ΘύρΜήΑΒWRAP_CONTENTϋψοϋπμϊ╗ξίΠΛxmlί╕Δί▒ΑόΨΘϊ╗╢ϋπμόηΡό╡ΒύρΜό╡ΖόηΡ(ϊ╕Λ)
2012-10-10 18:14 1167... -
Androidϊ╕φmeasureϋ┐ΘύρΜήΑΒWRAP_CONTENTϋψοϋπμϊ╗ξίΠΛxmlί╕Δί▒ΑόΨΘϊ╗╢ϋπμόηΡό╡ΒύρΜό╡ΖόηΡ(ϊ╕Μ)
2012-10-17 20:05 862... -
Androidϊ╕φόΨΘϊ╗╢ώΑΚόΜσίβρύγΕίχηύΟ░
2012-11-30 08:59 1173... -
ήΑΡύ╝ΨϋψΣίΟθύΡΗήΑΣϊ╜┐ύΦρLexί░ΗC/C++όΨΘϊ╗╢ϋ╛ΥίΘ║ϊ╕║HTMLόΨΘϊ╗╢
2012-07-20 09:37 107008ί╣┤9όεΙίΖξίφοΎ╝Ν12ί╣┤7όεΙόψΧϊ╕γΎ╝Νύ╗Υόζθϊ║ΗόΙΣίερϋ╜ψϊ╗╢ίφοώβλόΕΚί┐τϊ╕░ίψΝύγΕίνπ ... -
ήΑΡύ╝ΨϋψΣίΟθύΡΗήΑΣόφμίΙβϋκρϋ╛╛ί╝Π
2012-07-21 21:49 230208ί╣┤9όεΙίΖξίφοΎ╝Ν12ί╣┤7όεΙόψΧϊ╕γΎ╝Νύ╗Υόζθϊ║ΗόΙΣίερϋ╜ψϊ╗╢ίφοώβλόΕΚί┐τϊ╕░ίψΝύγΕίνπ ... -
ήΑΡOpenCVήΑΣϋχ┐ώΩχMatίδ╛ίΔΠϊ╕φόψΠϊ╕ςίΔΠύ┤ιύγΕίΑ╝
2012-07-22 07:10 1171ϊ╗Λίνσύβ╛ί║οόΡεϋ╡ΕόΨβϋ┐αόΡείΙ░ϊ║ΗϋΘςί╖▒ύγΕήΑΓήΑΓήΑΓήΑΛϋχ┐ώΩχίδ╛ίΔΠϊ╕φόψΠϊ╕ςίΔΠύ┤ιύγΕίΑ╝ ... -
ήΑΡύ╝ΨϋψΣίΟθύΡΗήΑΣύΦρYaccίΒγϋψφό│ΧίΙΗόηΡ
2012-07-23 05:47 177308ί╣┤9όεΙίΖξίφοΎ╝Ν12ί╣┤7όεΙόψΧϊ ... -
ήΑΡUMLήΑΣUMLίΘιύπΞίδ╛ύγΕύ╗αίΙ╢
2012-07-24 09:49 99008ί╣┤9όεΙίΖξίφοΎ╝Ν12ί╣┤7όεΙόψΧϊ╕γΎ╝Νύ╗Υόζθϊ║ΗόΙΣίερϋ╜ψϊ╗╢ίφοώβλόΕΚί┐τϊ╕░ίψΝύγΕίνπ ... -
ήΑΡOpenCVήΑΣώΓ╗ίθθό╗νό│λΎ╝γόΨ╣όκΗήΑΒώταόΨψήΑΒϊ╕φίΑ╝ήΑΒίΠΝϋ╛╣ό╗νό│λ
2012-07-26 10:52 1459ώΓ╗ίθθό╗νό│λΎ╝ΙίΞ╖ύπψΎ╝Κ ώΓ╗ίθθύχΩίφΡίΑ╝ίΙσύΦρύ╗βίχγίΔΠύ┤ι ... -
ήΑΡόΧ░όΞχύ╗ΥόηΕήΑΣόΟΤί║ΠύχΩό│ΧΎ╝γί╕Νί░ΦήΑΒί╜Τί╣╢ήΑΒί┐τώΑθήΑΒίιΗόΟΤί║Π
2012-07-28 06:15 102508ί╣┤9όεΙίΖξίφοΎ╝Ν12ί╣┤7όεΙόψΧϊ ... -
ήΑΡOpenCVήΑΣϋπΤύΓ╣όμΑό╡ΜΎ╝γHarrisϋπΤύΓ╣ίΠΛShi-TomasiϋπΤύΓ╣όμΑό╡Μ
2012-07-31 13:25 1546ϋπΤύΓ╣ ύΚ╣ί╛ΒόμΑό╡Μϊ╕ΟίΝ╣ώΖΞόα ... -
ήΑΡUMLήΑΣόκΙϊ╛ΜίΙΗόηΡΎ╝γόε║ίε║ϋ┐Ρϊ╜εύ│╗ύ╗θ
2012-08-01 17:22 313308ί╣┤9όεΙίΖξίφοΎ╝Ν12ί╣┤7όεΙόψΧϊ ...





ύδ╕ίΖ│όΟρϋΞΡ
ίερϋ┐βϊ╕ςίΟΜύ╝σίΝΖϊ╕φΎ╝ΝόΙΣϊ╗υίΠψϊ╗ξύεΜίΙ░ίΘιϊ╕ςίΖ│ώΦχύγΕϊ╕╗ώλαΎ╝ΝίΝΖόΜυέΑεόεΚίδ╛έΑζήΑΒέΑεϊ║ΝίΠΚόιΣέΑζήΑΒέΑεAVLόιΣέΑζϊ╗ξίΠΛέΑεόεΑύθφϋ╖ψί╛ΕέΑζΎ╝Νϋ┐βϊ║δώΔ╜όαψόΧ░όΞχύ╗ΥόηΕίΤΝύχΩό│ΧώλΗίθθύγΕώΘΞϋοΒόοΓί┐╡ήΑΓ ώοΨίΖΙΎ╝ΝόΙΣϊ╗υόζξό╖▒ίΖξύΡΗϋπμϊ╕Αϊ╕ΜέΑεϊ║ΝίΠΚόιΣέΑζήΑΓϊ║ΝίΠΚόιΣόαψϊ╕ΑύπΞύΚ╣όχΛύγΕόΧ░όΞχύ╗ΥόηΕ...
ίερϋ┐βϊ╕ςϊ╕╗ώλαϊ╕φΎ╝ΝόΙΣϊ╗υί░ΗόΟλϋχρϊ╕ΚύπΞύΚ╣όχΛύγΕόιΣύ▒╗ίηΜΎ╝γόΟΤί║Πϊ║ΝίΠΚόιΣήΑΒAVLόιΣίΤΝίΥΙίντόδ╝όιΣΎ╝Νϊ╗ξίΠΛίοΓϊ╜Χϊ╜┐ύΦρJavaϋψφϋρΑόζξίχηύΟ░ίχΔϊ╗υύγΕίθ║όευόΥΞϊ╜εΎ╝ΝίοΓίληήΑΒίΙιήΑΒόΦ╣ήΑΒόθξήΑΓ ώοΨίΖΙΎ╝ΝόΟΤί║Πϊ║ΝίΠΚόιΣΎ╝ΙSorted Binary TreeΎ╝Κόαψϊ╕ΑύπΞύΚ╣όχΛύγΕϊ║ΝίΠΚόιΣΎ╝ΝίΖ╢ϊ╕φόψΠϊ╕ς...
javaόΧ░όΞχύ╗ΥόηΕϊ╕ΟύχΩό│Χϊ╣Μί╣│ϋκκϊ║ΝίΠΚόιΣAVLόιΣύγΕϋχ╛ϋχκϊ╕ΟίχηύΟ░ίΙΗόηΡ.doc
CϋψφϋρΑόΧ░όΞχύ╗ΥόηΕϊ╣Μί╣│ϋκκϊ║ΝίΠΚόιΣΎ╝ΙAVLόιΣΎ╝ΚίχηύΟ░όΨ╣ό│Χύν║ϊ╛Μ όευόΨΘί░Ηϋψού╗Ηϊ╗Μύ╗ΞCϋψφϋρΑόΧ░όΞχύ╗ΥόηΕϊ╣Μί╣│ϋκκϊ║ΝίΠΚόιΣΎ╝ΙAVLόιΣΎ╝ΚίχηύΟ░όΨ╣ό│ΧΎ╝Νί╣╢ύ╗ΥίΡΙίχηϊ╛Μί╜λί╝ΠίΙΗόηΡϊ║ΗCϋψφϋρΑί╣│ϋκκϊ║ΝίΠΚόιΣύγΕύδ╕ίΖ│ίχγϊ╣Κϊ╕Οϊ╜┐ύΦρόΛΑί╖πήΑΓ ύθξϋψΗύΓ╣ϊ╕ΑΎ╝γAVLόιΣύγΕίχγϊ╣Κ AVLόιΣόαψϊ╕ΑύπΞ...
ίφοϊ╣ιίΤΝόΟΝόΠκAVLόιΣύγΕίΟθύΡΗίΤΝίχηύΟ░Ύ╝Νίψ╣ϊ║ΟύΡΗϋπμίΤΝί║ΦύΦρόΧ░όΞχύ╗ΥόηΕόεΚόηΒίνπύγΕί╕χίΛσήΑΓώΑγϋ┐ΘώαΖϋψ╗ίΤΝίΙΗόηΡόΠΡϊ╛δύγΕϊ╗μύιΒΎ╝ΝίΠψϊ╗ξίΛιό╖▒ίψ╣AVLόιΣίχηώβΖόΥΞϊ╜εύγΕύΡΗϋπμΎ╝Νϋ┐βίψ╣ϊ║Οϋ╜ψϊ╗╢ί╝ΑίΠΣΎ╝Νί░νίΖ╢όαψώεΑϋοΒί┐τώΑθόθξόΚ╛ίΤΝόδ┤όΨ░όΧ░όΞχύγΕίε║όβψΎ╝Νόαψώζηί╕╕όεΚϊ╗╖ίΑ╝ύγΕήΑΓ
ϊ║ΝίΠΚόιΣόεΚίνγύπΞύ▒╗ίηΜΎ╝ΝίοΓίχΝίΖρϊ║ΝίΠΚόιΣήΑΒό╗κϊ║ΝίΠΚόιΣίΤΝί╣│ϋκκϊ║ΝίΠΚόιΣΎ╝ΙίοΓAVLόιΣίΤΝύ║λώ╗ΣόιΣΎ╝ΚήΑΓίερC++ϊ╕φΎ╝Νϊ║ΝίΠΚόιΣίΠψϊ╗ξώΑγϋ┐Θύ╗ΥόηΕϊ╜ΥόΙΨύ▒╗όζξίχηύΟ░Ύ╝ΝόψΠϊ╕ςϋΛΓύΓ╣ίΝΖίΡτϊ╕Αϊ╕ςίΑ╝ήΑΒϊ╕Αϊ╕ςόΝΘίΡΣί╖οίφΡϋΛΓύΓ╣ύγΕόΝΘώΤΙίΤΝϊ╕Αϊ╕ςόΝΘίΡΣίΠ│ίφΡϋΛΓύΓ╣ύγΕόΝΘώΤΙήΑΓί╕╕ϋπΒύγΕόΥΞϊ╜είΝΖόΜυόΠΤίΖξ...
όευϋψζώλαϊ╕╗ϋοΒόΟλϋχρϊ║ΗC++ίχηύΟ░ύγΕϊ║ΝίΠΚόιΣήΑΒϊ║ΝίΠΚόΡεύ┤λόιΣϊ╗ξίΠΛAVLόιΣΎ╝Νϋ┐βϊ║δώΔ╜όαψώταύ║πόΧ░όΞχύ╗ΥόηΕΎ╝Νίψ╣ϊ║Οϊ╝αίΝΨύχΩό│ΧίΤΝόΠΡώταύρΜί║ΠόΧΙύΟΘϋΘ│ίΖ│ώΘΞϋοΒήΑΓ ϊ║ΝίΠΚόιΣόαψϊ╕ΑύπΞύΚ╣όχΛύγΕόιΣύ╗ΥόηΕΎ╝ΝόψΠϊ╕ςϋΛΓύΓ╣όεΑίνγίΠςόεΚϊ╕νϊ╕ςίφΡϋΛΓύΓ╣Ύ╝ΝώΑγί╕╕ίΙΗϊ╕║ί╖οίφΡϋΛΓύΓ╣ίΤΝίΠ│ίφΡϋΛΓύΓ╣ήΑΓίερ...
όθξόΚ╛όΥΞϊ╜είΙβόαψίερόεΚί║ΠύγΕϊ║ΝίΠΚόιΣϊ╕φϋ┐δϋκΝύ║┐όΑπόΡεύ┤λΎ╝ΝAVLόιΣύγΕώταί║οί╣│ϋκκϊ╜┐ί╛ΩόθξόΚ╛όΧΙύΟΘώταήΑΓ 2. **AVLόιΣύγΕόΩΜϋ╜υόΥΞϊ╜ε**Ύ╝γίΙΗϊ╕║ίδδύπΞύ▒╗ίηΜέΑΦέΑΦί╖οόΩΜήΑΒίΠ│όΩΜήΑΒί╖οίΠ│όΩΜίΤΝίΠ│ί╖οόΩΜΎ╝ΝύΦρϊ║ΟίερόΠΤίΖξίΤΝίΙιώβνίΡΟόΒλίνΞόιΣύγΕί╣│ϋκκήΑΓϊ╛ΜίοΓΎ╝Νί╜Υϊ╕Αϊ╕ςϋΛΓύΓ╣ύγΕί╖οίφΡόιΣ...
ίερόευϊ╕╗ώλαϊ╕φΎ╝ΝόΙΣϊ╗υί░Ηό╖▒ίΖξόΟλϋχρέΑεόιΣ_όΧ░όΞχύ╗ΥόηΕϊ║ΝίΠΚόιΣίΤΝόιΣύγΕύδ╕ίΖ│όΥΞϊ╜ε_έΑζόΚΑό╢╡ύδΨύγΕύθξϋψΗύΓ╣ήΑΓ ώοΨίΖΙΎ╝ΝόΙΣϊ╗υϋοΒϊ║Ηϋπμϊ╗Αϊ╣ΙόαψόιΣήΑΓόιΣόαψϊ╕ΑύπΞώζηύ║┐όΑπύγΕόΧ░όΞχύ╗ΥόηΕΎ╝ΝίχΔύΦ▒ϊ╕Αύ╗ΕϋΛΓύΓ╣Ύ╝ΙόΙΨύπ░ϊ╕║ώκ╢ύΓ╣Ύ╝ΚίΤΝϋ┐ηόΟξϋ┐βϊ║δϋΛΓύΓ╣ύγΕϋ╛╣ύ╗ΕόΙΡήΑΓόψΠϊ╕ςϋΛΓύΓ╣ίΠψϊ╗ξόεΚώδ╢ϊ╕ς...
AVLόιΣί╕╕ύΦρϊ║ΟόΧ░όΞχί║Υύ┤λί╝ΧήΑΒόΨΘϊ╗╢ύ│╗ύ╗θήΑΒύ╝ΨϋψΣίβρύυοίΠ╖ϋκρύφΚίε║όβψΎ╝ΝώεΑϋοΒώταόΧΙόθξόΚ╛ίΤΝϊ┐ζόΝΒόΧ░όΞχύ╗ΥόηΕί╣│ϋκκύγΕίε║ίΡΙήΑΓ **όΑ╗ύ╗ΥΎ╝γ** AVLόιΣϊ╜εϊ╕║ϋΘςί╣│ϋκκϊ║ΝίΠΚόΡεύ┤λόιΣύγΕϊ╗μϋκρΎ╝ΝώΑγϋ┐Θί╣│ϋκκίδιίφΡίΤΝόΩΜϋ╜υόΥΞϊ╜εϊ┐ζϋψΒϊ║Ηώταί║οί╣│ϋκκΎ╝ΝόΠΡώταϊ║ΗόθξόΚ╛ήΑΒόΠΤίΖξίΤΝίΙιώβν...
*avlόιΣΎ╝γϊ╕ΑύπΞϋΘςί╣│ϋκκϊ║ΝίΠΚόιΣΎ╝ΝίχΔίΠψϊ╗ξίερόΠΤίΖξήΑΒίΙιώβνίΤΝόθξόΚ╛όΥΞϊ╜εϊ╕φϊ┐ζόΝΒί╣│ϋκκήΑΓ * όΟΤί║Πϊ║ΝίΠΚόιΣΎ╝γϊ╕ΑύπΞϊ║ΝίΠΚόιΣΎ╝ΝίχΔύγΕόψΠϊ╕ςϋΛΓύΓ╣ύγΕίΑ╝ώΔ╜ί░Πϊ║ΟόΙΨύφΚϊ║ΟίχΔύγΕί╖οίφΡόιΣϊ╕φύγΕόΚΑόεΚϋΛΓύΓ╣ύγΕίΑ╝ήΑΓ ϊ║ΝίΠΚόιΣύγΕόΥΞϊ╜εΎ╝γ * όΠΤίΖξόΥΞϊ╜εΎ╝γίερϊ║ΝίΠΚόιΣϊ╕φόΠΤίΖξϊ╕Αϊ╕ςόΨ░...
ί╣│ϋκκόεΚί║Πϊ║ΝίΠΚόιΣΎ╝Νϊ╣θύπ░ϊ╕║AVLόιΣΎ╝Νόαψϊ║ΝίΠΚόΡεύ┤λόιΣύγΕϊ╕ΑύπΞ...όΑ╗ϊ╣ΜΎ╝ΝAVLόιΣόαψϊ╕ΑύπΞώταόΧΙύγΕόΧ░όΞχύ╗ΥόηΕΎ╝ΝώΑΓύΦρϊ║ΟώεΑϋοΒί┐τώΑθόθξόΚ╛ήΑΒόΠΤίΖξίΤΝίΙιώβνόΥΞϊ╜εύγΕίε║όβψήΑΓώΑγϋ┐ΘύΡΗϋπμίΖ╢ί╣│ϋκκίδιίφΡήΑΒόΩΜϋ╜υόΥΞϊ╜εϊ╗ξίΠΛόΠΤίΖξίΤΝίΙιώβνύγΕώΑ╗ϋ╛ΣΎ╝ΝίΠψϊ╗ξόδ┤ίξ╜ίε░όΟΝόΠκίΤΝί║ΦύΦρAVLόιΣήΑΓ
ίερϋχκύχΩόε║ύπΣίφοϊ╕φΎ╝ΝAVLόιΣόαψόεΑίΖΙίΠΣόαΟύγΕϋΘςί╣│ϋκκϊ║ΝίΠΚόθξόΚ╛όιΣήΑΓίερAVLόιΣϊ╕φϊ╗╗ϊ╜ΧϋΛΓύΓ╣ύγΕϊ╕νϊ╕ςίφΡόιΣύγΕώταί║οόεΑίνπί╖χίΙτϊ╕║1Ύ╝ΝόΚΑϊ╗ξίχΔϊ╣θϋλτύπ░ϊ╕║ώταί║οί╣│ϋκκόιΣήΑΓίληίΛιίΤΝίΙιώβνίΠψϋΔ╜ώεΑϋοΒώΑγϋ┐Θϊ╕ΑόυκόΙΨίνγόυκόιΣόΩΜϋ╜υόζξώΘΞόΨ░ί╣│ϋκκϋ┐βϊ╕ςόιΣήΑΓAVLόιΣί╛ΩίΡΞϊ║ΟίχΔύγΕίΠΣόαΟϋΑΖ...
AVL όιΣόαψϊ╕ΑύπΞώταόΧΙύγΕόΧ░όΞχύ╗ΥόηΕΎ╝ΝίΠψϊ╗ξϊ┐ζόΝΒόΠΤίΖξήΑΒίΙιώβνίΤΝόΡεύ┤λόΥΞϊ╜εύγΕόΧΙύΟΘήΑΓώΑγϋ┐Θϊ║Ηϋπμ AVL όιΣύγΕίχγϊ╣ΚήΑΒύ╗ΥόηΕήΑΒί╣│ϋκκίδιίφΡήΑΒόΩΜϋ╜υόΥΞϊ╜είΤΝόΠΤίΖξήΑΒίΙιώβνόΥΞϊ╜εύφΚύδ╕ίΖ│ύθξϋψΗύΓ╣Ύ╝ΝόΙΣϊ╗υίΠψϊ╗ξόδ┤ίξ╜ίε░ί║ΦύΦρ AVL όιΣϋπμίΗ│ίχηώβΖώΩχώλαήΑΓ
ίερόΧ░όΞχύ╗ΥόηΕύγΕίφοϊ╣ιϊ╕φΎ╝ΝύΡΗϋπμί╣╢όΟΝόΠκAVLόιΣύγΕόοΓί┐╡ήΑΒύΚ╣όΑπϊ╗ξίΠΛόΥΞϊ╜εόαψϋΘ│ίΖ│ώΘΞϋοΒύγΕήΑΓ ί╣│ϋκκϊ║ΝίΠΚόιΣύγΕόοΓί┐╡Ύ╝γ ί╣│ϋκκϊ║ΝίΠΚόιΣύγΕϊ╕╗ϋοΒύδχόιΘόαψϋπμίΗ│όβχώΑγϊ║ΝίΠΚόΡεύ┤λόιΣίΠψϋΔ╜ϊ║πύΦθύγΕώταί║οϊ╕Ξί╣│ϋκκώΩχώλαΎ╝Νϊ╗ξόΠΡώταόθξόΚ╛ήΑΒόΠΤίΖξίΤΝίΙιώβνόΥΞϊ╜εύγΕόΧΙύΟΘήΑΓίερAVLόιΣϊ╕φ...
ίχηώςΝόΛξίΣΛίΠψϋΔ╜ϊ╝γϋψού╗ΗϋπμώΘΛϋ┐βϊ║δόΥΞϊ╜εύγΕόφξώςνΎ╝ΝίΝΖόΜυίοΓϊ╜ΧόηΕί╗║ϊ║ΝίΠΚόθξόΚ╛όιΣΎ╝ΝίοΓϊ╜ΧίχηύΟ░AVLόιΣύγΕόΩΜϋ╜υύχΩό│ΧΎ╝Νϊ╗ξίΠΛίοΓϊ╜ΧίερίχηώβΖί║ΦύΦρϊ╕φϊ╜┐ύΦρϋ┐βϊ║δόΧ░όΞχύ╗ΥόηΕήΑΓόφνίνΨΎ╝ΝόΛξίΣΛίΠψϋΔ╜ϋ┐αϊ╝γίΝΖίΡτίχηώςΝύ╗ΥόηεύγΕίΙΗόηΡΎ╝ΝόψΦίοΓϊ╕ΞίΡΝόΥΞϊ╜εύγΕϋ┐ΡϋκΝόΩ╢ώΩ┤όψΦϋ╛ΔΎ╝Νϊ╗ξίΠΛϊ╕Ξ...
όευίχηώςΝύγΕϊ╕╗ώλαόαψέΑεϊ║ΝίΠΚόιΣέΑζΎ╝Νϋ┐βόαψόΧ░όΞχύ╗ΥόηΕϊ╕φϊ╕Αϊ╕ςίθ║ύκΑϊ╕ΦώΘΞϋοΒύγΕόοΓί┐╡ήΑΓϊ║ΝίΠΚόιΣόαψϊ╕ΑύπΞώζηύ║┐όΑπύγΕόΧ░όΞχύ╗ΥόηΕΎ╝ΝύΦ▒ϋΛΓύΓ╣Ύ╝ΙόΙΨύπ░ϊ╕║ώκ╢ύΓ╣Ύ╝Κύ╗ΕόΙΡΎ╝ΝόψΠϊ╕ςϋΛΓύΓ╣όεΑίνγόεΚϊ╕νϊ╕ςίφΡϋΛΓύΓ╣Ύ╝ΝώΑγί╕╕ύπ░ϊ╕║ί╖οίφΡϋΛΓύΓ╣ίΤΝίΠ│ίφΡϋΛΓύΓ╣ήΑΓϋ┐βϊ╕ςίχηώςΝόΩρίερί╕χίΛσίφούΦθό╖▒ίΖξύΡΗϋπμ...
ίερίχηώβΖί║ΦύΦρϊ╕φΎ╝Νϊ║ΝίΠΚόιΣύγΕίΙδί╗║ίΠψϋΔ╜ϋ┐αίΝΖόΜυόΠΤίΖξόΨ░ϋΛΓύΓ╣ήΑΒί╣│ϋκκϋ░ΔόΧ┤Ύ╝ΙίοΓAVLόιΣίΤΝύ║λώ╗ΣόιΣΎ╝ΚήΑΒώΒΞίΟΗΎ╝ΙίΚΞί║ΠήΑΒϊ╕φί║ΠήΑΒίΡΟί║ΠΎ╝ΚύφΚόΥΞϊ╜εήΑΓϋ┐βϊ║δόΥΞϊ╜εώΔ╜ώεΑϋοΒίψ╣ϊ║ΝίΠΚόιΣύγΕόΑπϋ┤ρόεΚό╖▒ίΖξύΡΗϋπμΎ╝Νί╣╢ϋΔ╜ύΒ╡ό┤╗ϋ┐ΡύΦρόΝΘώΤΙίΤΝί╝ΧύΦρήΑΓ όΑ╗ύ╗Υϋ╡╖όζξΎ╝Νϊ║ΝίΠΚόιΣύγΕίΙδί╗║...
6. **ί╣│ϋκκϊ║ΝίΠΚόιΣ**Ύ╝γίοΓAVLόιΣίΤΝύ║λώ╗ΣόιΣΎ╝ΝίχΔϊ╗υϊ┐ζόΝΒϊ╕ΑίχγύγΕί╣│ϋκκόΑπΎ╝Νύκχϊ┐ζόθξόΚ╛όΧΙύΟΘήΑΓίερC++ϊ╕φίχηύΟ░ϋ┐βύ▒╗όιΣώεΑϋοΒώλζίνΨύγΕόΩΜϋ╜υόΥΞϊ╜εόζξύ╗┤όΛνί╣│ϋκκήΑΓ 7. **όιΣύγΕό╖▒ί║οϊ╝αίΖΙόΡεύ┤λΎ╝ΙDFSΎ╝ΚίΤΝί╣┐ί║οϊ╝αίΖΙόΡεύ┤λΎ╝ΙBFSΎ╝Κ**Ύ╝γϊ║ΝίΠΚόιΣύγΕώΒΞίΟΗίΠψϊ╗ξύεΜϊ╜εόαψDFS...
όιΘώλαϊ╕φύγΕέΑεc++όΧ░όΞχύ╗ΥόηΕϊ║ΝίΠΚόιΣόΚΑόεΚίΛθϋΔ╜ύγΕό║ΡύιΒέΑζϋκρόαΟϋ┐βόαψϊ╕Αϊ╕ςύΦρC++ύ╝ΨύρΜϋψφϋρΑύ╝ΨίΗβύγΕϊ║ΝίΠΚόιΣίχηύΟ░Ύ╝ΝίΝΖίΡτϊ║Ηϊ║ΝίΠΚόιΣύγΕίΡΕύπΞόΥΞϊ╜εήΑΓC++όαψϊ╕ΑύπΞί╝║ύ▒╗ίηΜήΑΒώζλίΡΣίψ╣ϋ▒κύγΕύ╝ΨύρΜϋψφϋρΑΎ╝ΝίχΔύγΕόρκόζ┐όε║ίΙ╢ίΤΝSTLΎ╝ΙόιΘίΘΗόρκόζ┐ί║ΥΎ╝Κϊ╜┐ί╛ΩίχηύΟ░ίνΞόζΓύγΕόΧ░όΞχύ╗ΥόηΕ...