- 浏览: 80739 次
- 性别:

- 来自: 南京
-

最新评论
-
amy929:
你好!我最近在做学mapreduce,可否发一份这个代码给我学 ...
MapReduce框架中矩阵相乘的算法思路及其实现 -
微笑春天:
楼主 你好 花了一晚上的时间看了下你这个算法的实现 说实话 我 ...
MapReduce框架中矩阵相乘的算法思路及其实现 -
gaycolour:
大大,同求完整代码!634677370@qq.com
MapReduce框架中矩阵相乘的算法思路及其实现 -
zarchary-10:
你好,同求完整代码,可否发份zzy07053437@163.c ...
MapReduce框架中矩阵相乘的算法思路及其实现 -
developerinit:
你好,最近也在研究mapreduce矩阵乘法,想看下你这个例子 ...
MapReduce框架中矩阵相乘的算法思路及其实现
一、快速排序的基本思想
设当前待排序的无序区为R[low..high],利用分治法可将快速排序的基本思想描述为:
①分解:
在R[low..high]中任选一个记录作为基准(Pivot),以此基准将当前无序区划分为左、右两个较小的子区间R[low..pivotpos-1)和R[pivotpos+1..high],并使左边子区间中所有记录的关键字均小于等于基准记录(不妨记为pivot)的关键字pivot.key,右边的子区间中所有记录的关键字均大于等于pivot.key,而基准记录pivot则位于正确的位置(pivotpos)上,它无须参加后续的排序。
注意:
划分的关键是要求出基准记录所在的位置pivotpos。划分的结果可以简单地表示为(注意pivot=R[pivotpos]):
R[low..pivotpos-1].keys≤R[pivotpos].key≤R[pivotpos+1..high].keys
其中low≤pivotpos≤high。
②求解:
通过递归调用快速排序对左、右子区间R[low..pivotpos-1]和R[pivotpos+1..high]快速排序。
完整的代码如下:
- #include<iostream>
- #include<stack>
- using namespace std;
- int partition( int *arr , int low , int high)
- {
- int pivo = arr[low];
- while (low < high)
- {
- while (low < high && arr[high] >= pivo)
- --high;
- arr[low] = arr[high];
- while (low < high && arr[low] <= pivo)
- ++low;
- arr[high] = arr[low];
- }
- arr[low] = pivo;
- return low;
- }
- // 快速排序 递归
- void qsort( int *arr , int low , int high)
- {
- if (low < high)
- {
- int pivo = partition(arr , low , high);
- qsort(arr , low , pivo-1);
- qsort(arr , pivo+1 , high);
- }
- }
- // 快速排序 非递归
- void qsort_no_recursive( int *arr , int low , int high)
- {
- stack<int >s;
- int pivo;
- if (low < high)
- {
- pivo = partition(arr , low , high);
- if (low < pivo - 1)
- {
- s.push(low);
- s.push(pivo-1);
- }
- if (pivo + 1 < high)
- {
- s.push(pivo+1);
- s.push(high);
- }
- while (!s.empty())
- {
- high = s.top();
- s.pop();
- low = s.top();
- s.pop();
- pivo = partition(arr , low , high);
- if (low < pivo - 1)
- {
- s.push(low);
- s.push(pivo-1);
- }
- if (pivo + 1 < high)
- {
- s.push(pivo+1);
- s.push(high);
- }
- }//while
- }//if
- }
- //简单示例
- int main( void )
- {
- int i , a[11] = {20,11,12,5,6,13,8,9,14,7,10};
- printf("排序前的数据为:\n" );
- for (i = 0 ; i < 11 ; ++i)
- printf("%d " ,a[i]);
- printf("\n" );
- //qsort(a , 0 , 10);
- qsort_no_recursive(a , 0 , 10);
- printf("排序后的数据为:\n" );
- for (i = 0 ; i < 11 ; ++i)
- printf("%d " ,a[i]);
- printf("\n" );
- return 0;
- }
希尔排序(Shell Sort)又称为缩小增量排序,输入插入排序算法,是对直接排序算法的一种改进。本文介绍希尔排序算法。
对于插入排序算法来说,如果原来的数据就是有序的,那么数据就不需要移动,而插入排序算法的效率主要消耗在数据的移动中。因此可知:如果数据的本身就是有序的或者本身基本有序,那么效率就会得到提高。
希尔排序的基本思想是:将需要排序的序列划分成为若干个较小的子序列,对子序列进行插入排序,通过则插入排序能够使得原来序列成为基本有序。这样通过对较小的序列进行插入排序,然后对基本有序的数列进行插入排序,能够提高插入排序算法的效率。
在希尔排序中首先解决的是子序列的选择问题。对于子序列的构成不是简单的分段,而是采取相隔某个增量的数据组成一个序列。 增量一般的选择原则是:取上一个增量的一半作为此次序列的划分增量。首次选择序列长度的一半 为增量。
先假如:数组的长度为10,数组元素为:25、19、6、58、34、10、7、98、160、0
整个希尔排序的算法过程如下如所示:
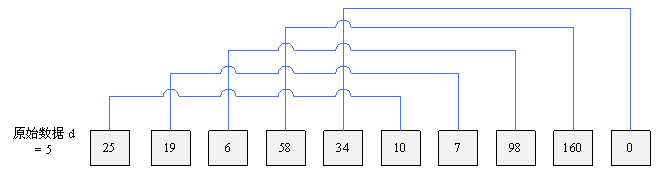
上图是原始数据和第一次选择的增量 d = 5。本次排序的结果如下图:
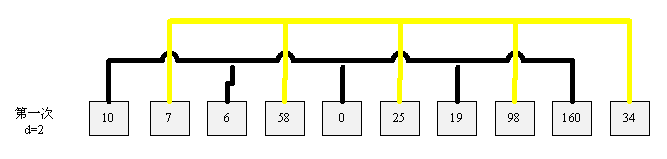
上图是第一次排序的结果,本次选择增量为 d=2。 本次排序的结果如下图:

当d=1 是进行最后一次排序,本次排序相当于冒泡排序的某一次循环。最终结果如下:

在实际使用过程中,带排序的数据肯定不是只有十个,但是上述是希尔排序的思想。其实希尔排序只是插入排序的一种优化。
C++实现希尔排序的代码如下所示:
- #include<iostream>
- using namespace std;
- void shell_sort( int array[] , int length)
- {
- int i , j , temp;
- int d = length/2; // 设置希尔排序的初始增量
- while (d >= 1)
- {
- for (i = d ; i < length ; ++i)
- {
- temp = array[i];
- j = i - d; // 步长为d的前面一个位置
- while (j >= 0 && array[j] > temp) // 从后往前进行插入排序
- {
- array[j + d] = array[j];
- j -= d;
- }
- array[j + d] = temp; // 找到了插入位置
- }
- d /= 2;
- }
- }
- int main( void )
- {
- int i , a[]={25,19,6,58,34,10,7,98,160,0};
- shell_sort(a , 10);
- for (i = 0 ; i < 10 ; ++i)
- cout<<a[i]<<" " ;
- cout<<endl;
- system("pause" );
- return 0;
- }
- // 模板
- template < class T> void ShellSort(T *a, int len) //希尔排序算法
- {
- int gap , j;
- for (gap = len / 2 ; gap > 0 ; gap /= 2)
- {
- for (j = gap;j < len ; ++j) //j从gap个元素开始
- {
- if (a[j] < a[j - gap]) //每个元素与自己组内的数据进行直接插入排序
- {
- T temp = a[j];
- int k = j - gap;
- while (k >= 0 && a[k] > temp)
- {
- a[k + gap] = a[k];
- k -= gap;
- }
- a[k + gap] = temp;
- }
- }
- }
- }
直接插入排序(direct Insert Sort)的基本思想是:顺序地将待排序的记录按其关键码的大小插入到已排序的记录子序列的适当位置。子序列的记录个数从1开始逐渐增大,当子序列的记录个数与顺序表中的记录个数相同时排序完毕。
- void InsertSort( int array[] , int length) // 无哨兵的插入排序
- {
- int i , j , temp;
- for (i = 1 ; i < length ; ++i)
- {
- if (array[i] < array[i-1])
- {
- temp = array[i];
- for (j = i - 1 ; j >= 0 && array[j] > temp ;--j)
- array[j + 1] = array[j];
- array[j + 1] = temp;
- }
- }
- }
- void InsertSort( int array[] , int length) // 有哨兵的插入排序
- {
- int i , j ;
- for (i = 1 ; i <= length ; ++i)
- {
- if (array[i] < array[i-1])
- {
- array[0] = array[i];
- for (j = i - 1 ; array[j] > array[0] ;--j)
- array[j + 1] = array[j];
- array[j + 1] = array[0];
- }
- }
- }
插入排序虽然在最坏情况下复杂性为O(n2),但是对于小规模输入来说,插入排序法是一个快速的排序法。从空间来看,它只需要一个元素的辅助空间,用于元素的位置交换O(1)。
(2)稳定性:
插入排序是稳定的;因为具有同一值的元素必然插在具有同一值得前一个元素的后面,即相对次序不变。
四、简单选择排序
简单选择排序的基本思想:第i趟简单选择排序是指通过n-i次关键字的比较,从n-i+1个记录中选出关键字最小的记录,并和第i个记录进行交换。共需进行i-1趟比较,直到所有记录排序完成为止。例如:进行第i趟选择时,从当前候选记录中选出关键字最小的k号记录,并和第i个记录进行交换。
实现代码如下:
- void SelectSort( int array[] , int length) // 简单选择排序
- {
- int i , j , k;
- for (i = 0 ; i < length-1 ; ++i)
- {
- k = i;
- for (j = i + 1 ; j < length ; ++j) // 从后面选择一个最小的记录
- {
- if (array[j] < array[k])
- k = j;
- }
- if (k != i) // 与第i个记录交换
- swap(array[i] , array[k]);
- }
- }
无论文件初始状态如何,在第i趟排序中选出最小关键字的记录,需做n-i次比较,因此,总的比较次数为:
n(n-1)/2=0(n2)
(2)记录的移动次数
当初始文件为正序时,移动次数为0
文件初态为反序时,每趟排序均要执行交换操作,总的移动次数取最大值3(n-1)。
直接选择排序的平均时间复杂度为O(n2)。
(3)直接选择排序是一个就地排序
(4)稳定性分析
直接选择排序是不稳定的。
【例】反例[2,2 ,1]
五、归并排序
- void Merge( int array[] , int low , int mid , int high)
- {
- int i , j , k;
- int *temp = ( int *)malloc((high - low + 1)* sizeof ( int ));
- i = low , j = mid + 1 , k = 0;
- while (i <= mid && j <= high)
- {
- if (array[i] < array[j]) // 进行排序存入动态分配的数组中
- temp[k++] = array[i++];
- else
- temp[k++] = array[j++];
- }
- while (i <= mid) // 如果前一半中还有未处理完的数据,按顺序移入动态分配的数组内
- temp[k++] = array[i++];
- while (j <= high) // 如果前一半中还有未处理完的数据,按顺序移入动态分配的数组内
- temp[k++] = array[j++];
- for (i = low , j = 0; i<= high ; ++i)
- array[i] = temp[j++];
- free(temp);
- }
- void Msort( int array[] , int low , int high)
- {
- int mid;
- if (low < high)
- {
- mid = (low + high)>>1;
- Msort(array , low , mid);
- Msort(array , mid + 1 , high);
- Merge(array , low , mid , high);
- }
- }
六、堆排序
- void HeapAdjust( int array[] , int s , int m) // 对堆进行调整,使下标从s到m的无序序列成为一个大顶堆
- {
- int j , temp = array[s];
- for (j = 2*s; j <= m ; j *= 2)
- {
- if (j < m && array[j] < array[j + 1]) // 如果结点的左孩子小于右孩子增加j的值
- ++j; // 用于记录较大的结点的下标
- if (temp >= array[j]) // 如果父结点大于等于两个孩子,则满足大顶堆的定义,跳出循环
- break ;
- array[s] = array[j]; // 否则用较大的结点替换父结点
- s = j; // 记录下替换父结点的结点下标
- }
- array[s] = temp; // 把原来的父结点移动到替换父结点的结点位置
- }
- void HeapSort( int array[] , int len)
- {
- int i;
- for (i = len / 2; i >= 0 ; --i) // 建立大顶堆
- HeapAdjust(array , i , len-1);
- for (i = len - 1 ; i > 0 ; --i)
- {
- swap(array[0] , array[i] ); // 第个元素和最后一个元素进行交换
- HeapAdjust(array , 0 , i-1); // 建立大顶堆
- }
- }
- // 将小元素冒泡到最前面,首先操作的是小元素
- void Bubble_Sort1( int array[] , int len)
- {
- int i , j;
- for (i = 0 ; i < len - 1 ; ++i)
- {
- for (j = i + 1 ; j < len ; ++j)
- {
- if (array[j] < array[i])
- swap(array[i] , array[j] );
- }
- }
- }
- // 将最大的元素冒泡到最后面
- void Bubble_Sort2( int array[] , int len)
- {
- int i , j;
- for (i = 0 ; i < len ; ++i) //注意和上面的算法对照此循环
- {
- for (j = 0 ; j < len - 1 - i ; ++j)
- {
- if (array[j] > array[j + 1])
- swap(array[j] , array[j+1] );
- }
- }
- }
- // 双向冒泡
- void Bubble_Sort3( int array[] , int len)
- {
- int left , right , i;
- left = 0 , right = len - 1;
- while (left < right)
- {
- for (i = left ; i < right ; ++i) // 从左到右冒泡
- {
- if (array[i + 1] < array[i])
- swap(array[i] , array[i+1]);
- }
- --right;
- for (i = right ; i > left ; --i) // 从右到左冒泡
- {
- if (array[i ] < array[i - 1])
- swap(array[i] , array[i-1]);
- }
- ++left;
- }
-
}
发表评论
-
不借助其它变量交换两变量值的三种算法
2012-10-16 10:27 1180在学习程序语言和进行程序设计的时候,交换两个变量的值是经常要使 ... -
编程珠玑开篇--磁盘文件排序问题
2012-10-16 10:07 1301转载。。。。 编程珠玑开篇--磁盘文件排序问题 ... -
各种排序算法的稳定性和时间复杂度小结
2012-10-16 09:22 1226各种排序算法的稳定性和时间复杂度小结 冒泡 ... -
求连通图中任意两个顶点的之间的所有路径
2012-03-15 22:08 0问题如图所示: 但是可能存在两种图,一种是DAG图,即深度遍 ... -
最大网络流的算法
2012-03-15 20:11 0网络最大流问题: ... -
HDFS的缺点以及相应的改进策略
2012-03-09 20:24 1326HDFS是一个不错的分布式 ... -
链表逆序输出---关于这一类型的问题
2012-03-08 22:02 0题目:输入一个链表的头结点,从尾到头反过来输出每个结点的值。链 ... -
求一个数列的最长非递增(递减)子序列
2012-03-09 16:22 8533问题描述: 给出� ... -
BFS与DFS
2012-03-04 18:10 0图深度遍历与广度遍历� ... -
字典树
2012-03-04 14:00 0trie树,即是我们所说的字典树。 典型应用是用于统计和排序 ... -
数列的排列与组合问题
2012-03-03 19:25 2743关于数列的全排列已经另外一篇文章中提到过了, 下面来介 ... -
字符串模式匹配--KMP算法
2012-03-03 09:43 0这个字符串模式匹配的算法在数据结构中可谓是非常的重要,也非常的 ... -
n-皇后以及全排列的问题--递归以及非递归的解法
2012-03-01 09:19 2457首先说下全排序的问题 这个问题可以说是最经典的问题, ... -
外排序学习(1)
2012-02-28 20:52 0首先对应到具体问题, 在网上见到的一个题目, 一个最多含有 ... -
关于链表追赶--链表中环的问题
2012-02-28 15:19 1745关于环的问题, 介绍� ... -
最大连续子数列的和问题
2012-02-28 10:57 0对应最常见的问题: 输入一个整形数组,数组里有正数也有 ... -
亲和数问题--伴随数组的简单应用
2012-02-27 22:30 0原题是求50000以内的所有亲和数;; 亲和数的定义如 ... -
在集合中寻找满足条件的两个或者多个数
2012-02-23 12:27 0对于这个类型的具体问题常见的有如下: 1.输入一个数组和一个 ... -
选取K个最小的数--学习报告
2012-02-22 19:27 0问题描述: 查找最小的k个元素 题目:输入n个整数 ... -
计数排序--小计
2012-02-21 13:48 0void CountingSort(const char *A ...





相关推荐
1.版本:matlab2014/2019a/2024a 2.附赠案例数据可直接运行。 3.代码特点:参数化编程、参数可方便更改、代码编程思路清晰、注释明细。 4.适用对象:计算机,电子信息工程、数学等专业的大学生课程设计、期末大作业和毕业设计。
内容概要:本文详细介绍了基于西门子1500PLC的汽车焊装生产线自动化控制系统的设计与实现。涵盖了硬件连接(如PLC、触摸屏、智能终端、机器人)、智能通信(Profinet、IO-Link、S7协议)以及高级算法的应用。具体包括设备命名规范、速度监测算法、机器人通信配置、GRAPH顺控程序、安全程序设计、MES系统通信等内容。文中还提供了具体的编程示例,展示了如何通过SCL、梯形图和STL等多种编程方式实现复杂的功能。 适合人群:从事工业自动化领域的工程师和技术人员,尤其是对PLC编程和自动化生产线有研究兴趣的人群。 使用场景及目标:适用于希望深入了解PLC编程、智能通信技术和自动化生产线集成的技术人员。目标是帮助读者掌握大型自动化项目的架构设计、编程技巧和故障排查方法。 其他说明:本文不仅提供理论知识,还包括大量实际操作经验分享,有助于提高读者的实际动手能力和解决问题的能力。
第五章矿井通风网络中风量分配与调节.ppt
第章--数据库基础知识-习题.doc
背景描述 2016 年全球生态足迹 您所在国家消耗的资源是否超过一年产生的资源? 数据说明 上下文 生态足迹衡量的是特定人口生产其消耗的自然资源(包括植物性食品和纤维产品、牲畜和鱼产品、木材和其他林产品、城市基础设施的空间)和吸收其废物(尤其是碳排放)所需的生态资产。该足迹跟踪了六类生产性表面积的使用情况:农田、牧场、渔场、建成区(或城市)土地、森林面积和土地上的碳需求。 一个国家的生物承载力代表其生态资产的生产力,包括农田、牧场、林地、渔场和建筑用地。这些区域,尤其是如果不采伐,也可以吸收我们产生的大部分废物,尤其是我们的碳排放。 生态足迹和生物承载力都以全球公顷表示,即具有全球可比性的标准化公顷数与世界平均生产力。 如果一个种群的生态足迹超过该地区的生物承载力,则该区域就会出现生态赤字。它对其陆地和海洋所能提供的商品和服务的需求——水果和蔬菜、肉类、鱼类、木材、服装用棉花和二氧化碳吸收——超过了该地区生态系统可以更新的需求。生态赤字地区通过进口、变现自己的生态资产(如过度捕捞)和/或向大气中排放二氧化碳来满足需求。如果一个地区的生物承载力超过其生态足迹,它就拥有生态保护区。 确认 生态足迹测量是由不列颠哥伦比亚大学的 Mathis Wackernagel 和 William Rees 构思的。生态足迹数据由 Global Footprint Network 提供。 灵感 您的国家是否存在生态赤字,消耗的资源超过了每年的产量?哪些国家的生态赤字或保护区最大?他们的消费量是比普通国家少还是多?2017 年地球超载日,即日历上人类使用一年自然资源的日子,何时发生?
内容概要:本文详细介绍了LabVIEW与欧姆龙PLC之间通过Ethernet/IP和TCP协议进行网络通讯的技术优势。文中强调了LabVIEW在自定义变量、字符串、数值(如I16、I32、Float、Double)、数组和BOOL类型数据读写方面的能力,指出其相比传统的Fins通讯更为优越。此外,文章展示了实际测试结果,证明了LabVIEW在这类通讯中的高准确度和稳定性。 适用人群:从事工业自动化领域的工程师和技术人员,尤其是那些需要在项目中集成LabVIEW与欧姆龙PLC设备的人群。 使用场景及目标:适用于希望优化现有控制系统或新建设备间通讯链路的专业人士。主要目标是利用LabVIEW的强大功能来增强系统的可靠性和效率,减少因数据传输不畅带来的问题。 其他说明:文中提供的程序源码为原创作品,已经过充分测试并证实可行。对于想要深入了解两者交互机制或者寻求具体实施方法的人来说是非常有价值的参考资料。
内容概要:本文详细介绍了SUMO(Simulation of Urban MObility)和CARLA(Open Source Simulator for Autonomous Driving)这两个重要仿真工具的联合仿真环境的安装与配置步骤。首先,分别讲解了SUMO和CARLA的安装流程及其环境配置,然后重点阐述了两者联合仿真的具体配置方法。接着,文章探讨了如何利用这一联合仿真环境进行自动驾驶的开发和驾驶模拟,包括自定义车辆模型、交通场景和交通规则等。此外,还深入讨论了强化学习在自动驾驶中的应用,如通过定义奖励函数和动作空间来训练和优化自动驾驶系统,以及轨迹预测技术的应用。最后,文章介绍了轨迹规划的关键技术和其实现方法,强调了其在自动驾驶路径规划和导航中的重要作用。 适合人群:从事自动驾驶技术研发的研究人员、开发人员及相关专业的学生。 使用场景及目标:①帮助研究人员和开发者搭建SUMO与CARLA联合仿真环境;②利用该环境进行自动驾驶系统的开发、测试和优化;③探索强化学习和轨迹预测在自动驾驶中的应用;④掌握自动驾驶系统中的轨迹规划技术。 阅读建议:本文不仅提供了详细的安装配置指导,还涵盖了自动驾驶技术的核心原理和技术方法,因此读者应在实践中逐步理解和应用这些内容,特别是在实际项目中尝试搭建和使用联合仿真环境。
应用密码学随堂测试.mhtml
短信系统网络结构及业务流程介绍.ppt
内容概要:本文探讨了基于分布式ADMM(交替方向乘子法)算法与碳排放交易的电力系统最优潮流调度问题。文中详细介绍了如何利用MATLAB和CPLEX/GUROBI平台进行仿真,包括系统分区、目标函数定义、ADMM主循环以及边界处理等方面的内容。通过将传统发电成本与碳交易成本相结合,提出了一种新的优化模型,旨在实现低碳调度的目标。实验结果显示,相较于传统集中式调度方式,该方法不仅降低了碳交易成本,还显著减少了区域间通信数据量,提高了系统的隐私性和鲁棒性。 适合人群:从事电力系统优化调度研究的专业人士,尤其是关注低碳经济和智能电网发展的研究人员和技术人员。 使用场景及目标:适用于需要解决电力系统中碳排放问题的研究项目或工程应用。具体目标包括降低碳排放成本、提高调度效率、减少区域间通信数据量以及增强系统稳定性。 其他说明:文中提供了详细的MATLAB代码示例,有助于读者理解和复现相关研究成果。此外,还提到了一些实用技巧,如自适应调整惩罚系数rho、正确配置CPLEX求解器参数等,对于实际操作具有重要指导意义。
内容概要:本文介绍了四平方和定理(拉格朗日定理)的编程实现方法及其优化思路。文章首先解释了四平方和定理的基本概念,即任意正整数可以表示为四个整数的平方和。接着,作者通过C++代码展示了如何将输入的整数逐步分解为四个平方数之和,具体步骤包括对输入整数进行开方取整并记录余数,然后对余数重复相同操作直到找到满足条件的四个平方数。此外,文中还提到为了提高运算效率,可以通过设置更严格的限制条件来减少不必要的计算,如使用数组保存每次运算结果,并根据特定规则更新数组中的值。最后,文章列举了一些具体的例子来验证算法的有效性,同时也指出了某些特殊情况需要额外处理,例如当余数为3时需额外增加两个1来满足六平方和的情况。 适合人群:具有C++编程基础的学习者或开发者,特别是对数学定理的编程实现感兴趣的读者。 使用场景及目标:①帮助读者理解四平方和定理的理论依据及其在编程中的应用;②指导读者如何通过编程实现数学定理,尤其是优化算法以提升计算效率。 其他说明:本文不仅提供了完整的C++代码示例,还详细解释了代码逻辑和优化策略,建议读者在阅读过程中结合实际编程练习,以便更好地掌握四平方和定理的编程实现方法。
省计算机等级考试试题汇编.doc
1.版本:matlab2014/2019a/2024a 2.附赠案例数据可直接运行。 3.代码特点:参数化编程、参数可方便更改、代码编程思路清晰、注释明细。 4.适用对象:计算机,电子信息工程、数学等专业的大学生课程设计、期末大作业和毕业设计。
第二章电子商务基本模式.ppt
电脑软件IT系统商务报告模版.pptx
电子政务安全中间件平台技术方案.doc