QuadTreeтЏЏтЈЅТаЉжАЙтљЇТђЮС╣Ѕт░▒Тў»ТаЉуіХуџёТЋ░ТЇ«у╗ЊТъё№╝їтЁХТ»ЈСИфУіѓуѓ╣ТюЅтЏЏСИфтГЕтГљУіѓуѓ╣№╝їтЈ»т░єС║їу╗┤т╣│жЮбжђњтйњтѕєтЅ▓тГљтї║тЪЪсђѓQuadTreeтИИућеС║јуЕ║жЌ┤ТЋ░ТЇ«т║Њу┤бт╝Ћ№╝ї3DуџёТцјСйЊтЈ»УДЂтї║тЪЪУБЂтЅф№╝їућџУЄ│тЏЙуЅЄтѕєТъљтцёуљє№╝їТѕЉС╗гС╗ітцЕС╗Іу╗ЇуџёТў»QuadTreeТюђтИИУбФТИИТѕЈжбєтЪЪСй┐ућетѕ░уџёуб░ТњъТБђТхІсђѓжЄЄућеQuadTreeу«ЌТ│Ћт░єтцДтцДтЄЈт░ЉжюђУдЂТхІУ»Ћуб░ТњъуџёТгАТЋ░№╝їС╗јУђїТЈљжФўТИИТѕЈтѕиТќ░ТђДУЃй№╝їТюгТќЄСЙІтГљтЪ║С║јHT for WebуџётЏЙтйбт╝ЋТЊј№╝їжђџУ┐ЄGraphViewтњїGraph3dViewтЁ▒С║ФтљїСИђТЋ░ТЇ«ТеАтъІDataModel№╝їтљїТЌХтЉѕуј░QuadTreeу«ЌТ│ЋСИІуџё2Dтњї3Dуб░ТњъУДєтЏЙТЋѕТъю№╝џhttp://v.youku.com/v_show/id_XODQyNTA1NjY0.htmlРђІ
QuadTreeуџёт«ъуј░ТюЅтЙѕтцџТѕљуєЪуџёуЅѕТюг№╝їТѕЉжђЅТІЕуџёТў»┬аhttps://github.com/timohausmann/quadtree-js/┬атЏЏтЈЅТаЉуџёу«ЌТ│ЋтЙѕу«ђтЇЋ№╝їтЏаТГцУ┐ЎСИфт╝ђТ║љт║ЊС╣Ът░▒СИцуЎЙТЮЦУАїС╗БуаЂсђѓСй┐ућеС╣ЪжЮътИИу«ђтЇЋ№╝їТъёт╗║СИђСИфQuadtreeт»╣У▒А№╝їуггСИђСИфтЈѓТЋ░С╝атЁЦrectС┐АТЂ»тѕХт«џТИИТѕЈуЕ║жЌ┤УїЃтЏ┤№╝їтюеТ»ЈТгАrequestAnimationFrameтѕиТќ░тИДТЌХ№╝їтЁѕжђџУ┐Єquadtree.clear()ТИЁжЎцУђЂТЋ░ТЇ«№╝їжђџУ┐Єquadtree.insert(rect)ТЈњтЁЦТќ░уџёУіѓуѓ╣уЪЕтйбтї║тЪЪ№╝їУ┐ЎТаиquadtreeт░▒тѕЮтДІтїќтЦйС║є№╝їтЅЕСИІт░▒Тў»Та╣ТЇ«жюђУдЂУ░Ѓућеquadtree.retrieve(rect)УјитЈќТїЄт«џуЪЕтйбтї║тЪЪСИІ№╝їСИјтЁХтЈ»УЃйуЏИС║цжюђУдЂТБђТхІуџёуЪЕтйбт»╣У▒АТЋ░у╗ёсђѓ
ТѕЉТъёт╗║С║єHTуџёGraphViewтњїGraph3dViewСИцСИфу╗ёС╗Х№╝їжђџУ┐Єht.widget.SplitViewтидтЈ│тѕєтЅ▓№╝їућ▒С║јСИцСИфУДєтЏЙжЃйтЁ▒С║ФтљїСИђDataModel№╝їтЏаТГцТѕЉС╗гтЅЕСИІуџётЁ│Т│еуѓ╣С╗ЁТў»т»╣DataModelуџёТЋ░ТЇ«ТЊЇСйю№╝їТъёт╗║С║є200СИфht.Nodeт»╣У▒А№╝їТ»ЈСИфт»╣У▒Ауџёattrт▒ъТђДСИіС┐ЮтГўС║єжџЈТю║уџёУ┐љтіеТќ╣тљЉvxтњїvy№╝їтљїТЌХС┐ЮтГўС║єт░єУдЂтЈЇтцЇТЈњтЁЦquadtreeуџёуЪЕтйбт»╣У▒А№╝їУ┐ЎТаижЂ┐тЁЇТ»ЈтИДТЏ┤Тќ░ТЌХтЈЇтцЇтѕЏт╗║т»╣У▒А№╝їтљїТЌХуЪЕтйбт»╣У▒АС╣Ът╝ЋућеС║єht.Nodeт»╣У▒А№╝їућеТЮЦтйЊжђџУ┐Єquadtree.retrieve(rect)УјитЈќжюђУдЂТБђТхІуџёуЪЕтйбт»╣У▒АТЌХ№╝їТѕЉС╗гУЃйТїЄт«џтЁХТЅђтЁ│УЂћуџёht.Nodeт»╣У▒А№╝їтЏаСИ║ТѕЉС╗гжюђУдЂт»╣Тюђу╗ѕТБђТхІСИ║уб░ТњъуџётЏЙтЁЃУ«Йуй«СИіу║бжбюУЅ▓уџёТЋѕТъю№╝їС╣Ът░▒Тў»ht.Nodeт╣│ТЌХТўЙуц║ж╗ўУ«цуџёУЊЮУЅ▓№╝їтйЊС║њуЏИуб░ТњъТЌХт░єТћ╣тЈўСИ║у║бУЅ▓сђѓ
жюђУдЂТ│еТёЈС╗јquadtree.retrieve(rect)УјитЈќжюђУдЂТБђТхІуџёуЪЕтйбт»╣У▒АТЋ░у╗ёСИГС╝џтїЁтљФУЄфУ║ФтЏЙтЁЃ№╝їтљїТЌХУ┐ЎС║ЏС╗ЁС╗ЁТў»тЈ»УЃйС╝џуб░ТњъуџётЏЙтЁЃ№╝їт╣ХСИЇТёЈтЉ│уЮђти▓у╗Јуб░ТњъС║є№╝їућ▒С║јТѕЉС╗гСЙІтГљТў»уЪЕтйб№╝їтЏаТГцжЄЄућеht.Default.intersectsRect(r1, r2)Тюђу╗ѕтѕцТќГТў»тљдуЏИС║ц№╝їтдѓТъюСйауџёСЙІтГљТў»тюєтйбтѕЎтЈ»С╗ЦжЄЄућеУ«Ау«ЌСИцСИфтюєт┐ЃУиЮуд╗Тў»тљдт░ЈС║јСИцСИфтЇітЙёТЮЦтє│т«џТў»тљдуЏИС║ц№╝їтЏаТГцТюђу╗ѕтѕцТќГуџёТаЄтЄєТа╣ТЇ«ТИИТѕЈу▒╗тъІС╝џТюЅти«т╝ѓсђѓ
жЄЄућеС║єQuadTreeУ┐ўТў»ТъЂтцДС║єТЈљжФўС║єУ┐љу«ЌТђДУЃй№╝їтљдтѕЎ100СИфтЏЙтЁЃт░▒жюђУдЂ100*100ТгАуџёуЏЉТхІ№╝їТѕЉУ┐ЎСИфСЙІтГљтю║ТЎ»СИІСИђУѕгС╣Ът░▒100*(10~30)уџёжЄЈ№╝џ
жЎцС║єуб░ТњъТБђТхІтцќQuadTreeу«ЌТ│ЋУ┐ўТюЅтЙѕтцџТюЅУХБуџёт║ћућежбєтЪЪ№╝їТюЅтЁ┤УХБтЈ»С╗ЦујЕујЕУ┐ЎСИф┬аhttps://github.com/fogleman/Quads
ТЅђТюЅС╗БуаЂтдѓСИІСЙЏтЈѓУђЃ№╝џ
function init(){
d = 200;
speed = 8;
dataModel = new ht.DataModel();
g3d = new ht.graph3d.Graph3dView(dataModel);
g2d = new ht.graph.GraphView(dataModel);
mainSplit = new ht.widget.SplitView(g3d, g2d);
mainSplit.addToDOM();
g2d.translate(300, 220);
g2d.setZoom(0.8, true);
for(var i=0; i<100; i++) {
var node = new ht.Node();
node.s3(randMinMax(5, 30), 10, randMinMax(5, 30));
node.p3(randMinMax(-d/2, d/2), 0, randMinMax(-d/2, d/2));
node.s({
'batch': 'group',
'shape': 'rect',
'shape.border.width': 1,
'shape.border.color': 'white',
'wf.visible': true,
'wf.color': 'white'
});
node.a({
vx: randMinMax(-speed, speed),
vy: randMinMax(-speed, speed),
obj: {
width: node.getWidth(),
height: node.getHeight(),
data: node
}
});
dataModel.add(node);
}
createShape([
{x: -d, y: d},
{x: d, y: d},
{x: d, y: -d},
{x: -d, y: -d},
{x: -d, y: d}
]);
quadtree = new Quadtree({ x: -d, y: -d, width: d, height: d });
requestAnimationFrame(update);
}
function update() {
quadtree.clear();
dataModel.each(function(data){
if(!(data instanceof ht.Shape)){
var position = data.getPosition();
var vx = data.a('vx');
var vy = data.a('vy');
var w = data.getWidth()/2;
var h = data.getHeight()/2;
var x = position.x + vx;
var y = position.y + vy;
if(x - w < -d){
data.a('vx', -vx);
x = -d + w;
}
if(x + w > d){
data.a('vx', -vx);
x = d - w;
}
if(y - h < -d){
data.a('vy', -vy);
y = -d + h;
}
if(y + h > d){
data.a('vy', -vy);
y = d - h;
}
data.setPosition(x, y);
var obj = data.a('obj');
obj.x = x - w;
obj.y = y - h;
quadtree.insert(obj);
setColor(data, undefined);
}
});
dataModel.each(function(data){
if(!(data instanceof ht.Shape)){
var obj = data.a('obj');
var objs = quadtree.retrieve(obj);
if(objs.length > 1){
for(var i=0; i<objs.length; i++ ) {
var data2 = objs[i].data;
if(data === data2){
continue;
}
if(ht.Default.intersectsRect(obj, data2.a('obj'))){
setColor(data, 'red');
setColor(data2, 'red');
}
}
}
}
});
requestAnimationFrame(update);
}
function randMinMax(min, max) {
return min + (Math.random() * (max - min));
}
function createShape(points){
shape = new ht.Shape();
shape.setPoints(points);
shape.setThickness(4);
shape.setTall(10);
shape.s({
'all.color': 'red',
'shape.background': null,
'shape.border.width': 2,
'shape.border.color': 'red'
});
dataModel.add(shape);
return shape;
}
function setColor(data, color){
data.s({
'all.color': color,
'shape.background': color
});
}
┬а



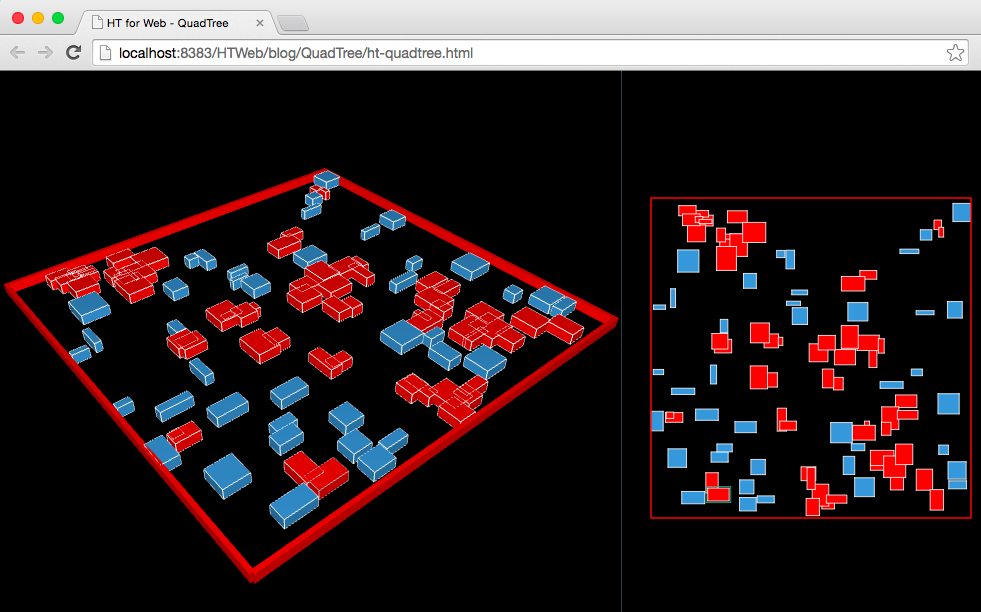
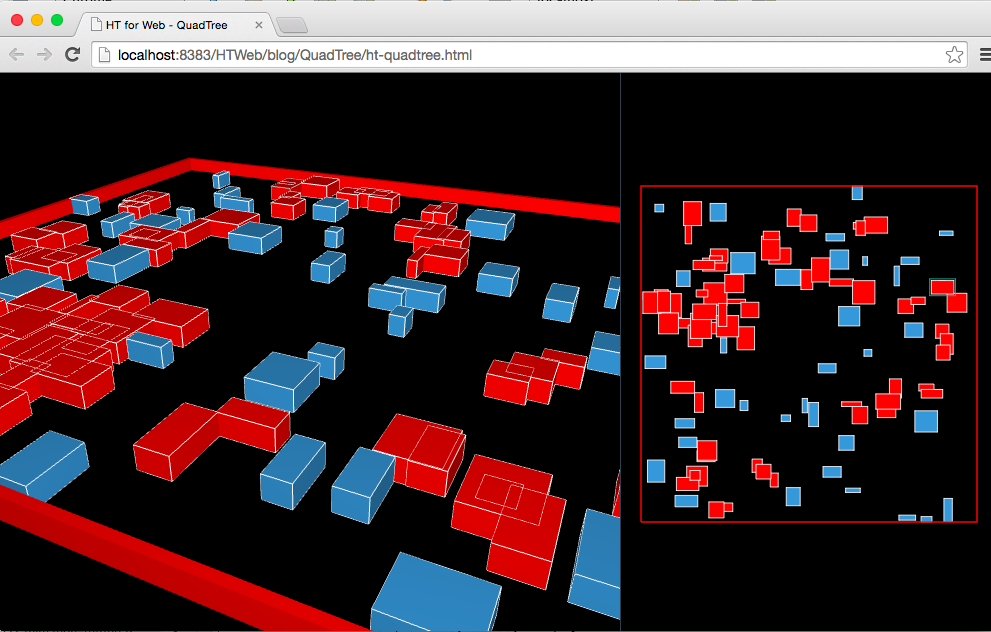




уЏИтЁ│ТјеУЇљ
Тђ╗С╣І№╝їУ┐ЎСИфC#т«ъуј░уџётЏЏтЈЅТаЉС╗БуаЂТЈљСЙЏС║єтѕЏт╗║сђЂу╗┤ТіцтњїСй┐ућетЏЏтЈЅТаЉу╗ЊТъёуџётіЪУЃй№╝їуЅ╣тѕФжђѓтљѕтцёуљє2DуЕ║жЌ┤СИГуџёуб░ТњъТБђТхІжЌ«жбўсђѓжђџУ┐ЄуљєУДБтњїт║ћућеУ┐ЎС║ЏТќЄС╗Х№╝їт╝ђтЈЉУђЁтЈ»С╗ЦТјїТЈАтЏЏтЈЅТаЉуџётЪ║ТюгтјЪуљє№╝їт╣Хт░єтЁХт║ћућеС║јт«ъжЎЁуџёжА╣уЏ«СИГ№╝їС╝ўтїќТђДУЃй№╝їТЈљтЇЄ...
creator тЏЏтЈЅТаЉ Quadtree.ts ућеС║јС╝ўтїќуб░ТњъТБђТхІ
тЏЏтЈЅТаЉ№╝ѕQuadtree№╝ЅТў»СИђуДЇТЋ░ТЇ«у╗ЊТъё№╝їуЅ╣тѕФжђѓућеС║јтюеС║їу╗┤уЕ║жЌ┤СИГу╗ёу╗Єтњїтцёуљєуѓ╣т»╣У▒АсђѓтюеУ«Ау«ЌТю║тЏЙтйбтГдсђЂтю░уљєС┐АТЂ»у│╗у╗ЪтњїтЏЙтЃЈтцёуљєуГЅжбєтЪЪСИГ№╝їтЏЏтЈЅТаЉУбФт╣┐Т│Џт║ћућесђѓт«Ѓу▒╗С╝╝С║јС║їтЈЅТаЉ№╝їСйєТ»ЈСИфУіѓуѓ╣ТюЅтЏЏСИфтГљУіѓуѓ╣№╝їтѕєтѕФС╗БУАеСИісђЂСИІсђЂтидсђЂ...
4. тЈ»УЃйУ┐ўтїЁтљФС║єтЈ»УДєтїќтЏЏтЈЅТаЉу╗ЊТъётњїуб░Тњъу╗ЊТъюуџёУЙЁтіЕС╗БуаЂ№╝їС╗ЦСЙ┐С║јУ░ЃУ»ЋтњїуљєУДБсђѓ Тђ╗уџёТЮЦУ»┤№╝їУ┐ЎСИфтЏЏтЈЅТаЉуб░ТњъТБђТхІуџёdemoТЈљСЙЏС║єСИђуДЇтюеAS3СИГС╝ўтїќтцДУДёТеАуЅЕСйЊуб░ТњъТБђТхІуџёУДБтє│Тќ╣ТАѕсђѓжђџУ┐ЄтЏЏтЈЅТаЉуџётѕњтѕєтњїТЪЦУ»б№╝їтЈ»С╗ЦТўЙУЉЌтЄЈт░ЉУ«Ау«ЌжЄЈ...
Сй┐ућетЏЏтЈЅТаЉУ┐ЏУАїу▓њтГљуб░ТњъТБђТхІсђѓ тЏЏтЈЅТаЉТў»СИђуДЇТаЉТЋ░ТЇ«у╗ЊТъё№╝їтЁХСИГТ»ЈСИфтєЁжЃеУіѓуѓ╣ТЂ░тЦйтЁиТюЅтЏЏСИфтГљУіѓуѓ╣сђѓ тЏЏтЈЅТаЉТў»тЁФтЈЅТаЉуџёС║їу╗┤ТеАТІЪ№╝їТюђтИИућеС║јжђџУ┐Єт░єС║їу╗┤уЕ║жЌ┤жђњтйњу╗єтѕєСИ║тЏЏСИфУ▒АжЎљТѕќтї║тЪЪТЮЦтѕњтѕєС║їу╗┤уЕ║жЌ┤сђѓ Т╝ћуц║уЅѕ тюеGitHubжАхжЮб...
тюеТаЄжбўРђюqur_tree.rar_quadtree image_тЏЏтЈЅТаЉ уѓ╣_тЏЏтЈЅТаЉтѕєтЅ▓_тЏЏтЈЅТаЉтЏЙтЃЈ_тЏЙтЃЈ тЏЏтЈЅТаЉРђЮСИГ№╝їтЁ│жћ«У»ЇРђютЏЏтЈЅТаЉ уѓ╣РђЮтњїРђютЏЏтЈЅТаЉтѕєтЅ▓РђЮТџЌуц║С║єУ┐ЎСИфтјІу╝ЕтїЁтЈ»УЃйтїЁтљФСИђСИфућеС║јтЏЏтЈЅТаЉтѕєтЅ▓тЏЙтЃЈСИГуЅ╣т«џуѓ╣уџётиЦтЁиТѕќу«ЌТ│ЋсђѓтЏЏтЈЅТаЉтѕєтЅ▓...
тЁХТгА№╝їтЏЏтЈЅТаЉ(Quadtree)Тў»СИђуДЇТЋ░ТЇ«у╗ЊТъё№╝їтИИућеС║јтЏЙтЃЈтѕєтЅ▓тњїтјІу╝ЕсђѓтюетЏЙтЃЈтцёуљєСИГ№╝їтЏЏтЈЅТаЉт░єтЏЙтЃЈуЕ║жЌ┤тѕњтѕєСИ║тцДт░ЈуЏИуГЅуџётЏЏУЙ╣тйбтї║тЪЪ№╝їт╣ХТа╣ТЇ«тї║тЪЪтєЁуџётЃЈу┤ауЏИС╝╝ТђДУ┐ЏУАїтѕєУДБсђѓтйЊСИђСИфтї║тЪЪтєЁтЃЈу┤ажбюУЅ▓уЏИУ┐ЉТЌХ№╝їУ»Цтї║тЪЪтЈ»С╗ЦУбФУ┐ЏСИђТГЦ...
тюеC#СИГт«ъуј░тЏЏтЈЅТаЉу«ЌТ│ЋтЈ»С╗ЦтИ«тіЕТѕЉС╗гжФўТЋѕтю░тцёуљєтцДжЄЈтѕєтИЃтюеС║їу╗┤т╣│жЮбСИіуџётЁЃу┤а№╝їТ»ћтдѓтюеТИИТѕЈт╝ђтЈЉСИГУ┐ЏУАїуб░ТњъТБђТхІТѕќтЏЙтЃЈтѕєтЅ▓уГЅС╗╗тіАсђѓ тЏЏтЈЅТаЉуџётЪ║ТюгТђЮТЃ│Тў»т░єуЕ║жЌ┤СИЇТќГтѕєтЅ▓ТѕљтЏЏСИфуЏИуГЅуџёжЃетѕє№╝їуЏ┤тѕ░Т»ЈСИфжЃетѕєтЈфтїЁтљФСИђСИфтЁЃу┤аТѕќУђЁСИ║...
сђітЪ║С║јжЎљтѕХтЏЏтЈЅТаЉуџётцДУДёТеАтю░тйбтЈ»УДєтїќтЈітЁХт«ъуј░сђІУ┐Ўу»ЄТќЄуї«Ти▒тЁЦТјбУ«еС║єтюетцёуљєтцДУДёТеАтю░тйбТЋ░ТЇ«ТЌХ№╝їтдѓСйЋтѕЕућежЎљтѕХтЏЏтЈЅТаЉт«ъуј░жФўТЋѕсђЂТхЂуЋЁуџётЈ»УДєтїќТіђТю»сђѓТюгТќЄт░єУ»ду╗єжўљУ┐░жЎљтѕХтЏЏтЈЅТаЉуџётЪ║ТюгТдѓт┐х№╝їС╗ЦтЈітЁХтюетю░тйбтЈ»УДєтїќСИГуџёт║ћуће№╝їтљїТЌХ...
тЏЏтЈЅТаЉ№╝ѕQuadtree№╝ЅТў»СИђуДЇТЋ░ТЇ«у╗ЊТъё№╝їтИИућеС║јтюеС║їу╗┤уЕ║жЌ┤СИГу╗ёу╗Єтњїу«Ауљєт»╣У▒А№╝їт░цтЁХтюеТИИТѕЈт╝ђтЈЉСИГ№╝їт«Ѓтюеуб░ТњъТБђТхІсђЂтЏЙтйбТИ▓ТЪЊС╝ўтїќуГЅТќ╣жЮбТюЅуЮђт╣┐Т│Џуџёт║ћућесђѓUnityТў»СИђТгЙТхЂУАїуџё3DТИИТѕЈт╝ЋТЊј№╝їт«ЃтЁЂУ«Ит╝ђтЈЉУђЁтѕЕућетљёуДЇу«ЌТ│ЋТЮЦТЈљжФўТИИТѕЈ...
6. **тЏЙтйбтїќУАеуц║**№╝џтюеUnityСИГ№╝їтЈ»С╗ЦжђџУ┐ЄтЈ»УДєтїќТќ╣т╝Јт▒Ћуц║тЏЏтЈЅТаЉуџёу╗ЊТъё№╝їУ┐ЎТюЅтіЕС║јуљєУДБтњїУ░ЃУ»ЋсђѓтЈ»УЃйСй┐ућеUnityуџё`OnDrawGizmos()`тЄйТЋ░ТЮЦу╗ўтѕХтЏЏтЈЅТаЉуџёУЙ╣уЋїтњїтГљтї║тЪЪсђѓ 7. **ТђДУЃйтѕєТъљ**№╝џжђџУ┐ЄтЏЏтЈЅТаЉ№╝їт╝ђтЈЉУђЁтЈ»С╗ЦТЏ┤тЦйтю░уљєУДБ...
тЏЏтЈЅТаЉ№╝ѕQuadtree№╝ЅТў»СИђуДЇТЋ░ТЇ«у╗ЊТъё№╝їуЅ╣тѕФжђѓућеС║јтюеС║їу╗┤уЕ║жЌ┤СИГу╗ёу╗Єтњїу«Ауљєт»╣У▒А№╝їт░цтЁХтюетцёуљєтЏЙтйбтњїтЏЙтЃЈтцёуљєжбєтЪЪ№╝їтдѓуб░ТњъТБђТхІсђЂтЮљТаЄТЪЦТЅЙтњїТ»ћт»╣уГЅТќ╣жЮбтЁиТюЅТўЙУЉЌС╝ўті┐сђѓтЏЏтЈЅТаЉТў»С║їтЈЅТаЉуџёТЅЕт▒Ћ№╝їТ»ЈСИфУіѓуѓ╣жЃйТюЅтЏЏСИфтГљУіѓуѓ╣№╝їтѕєтѕФ...
тЏЏтЈЅТаЉтЈ»С╗ЦућеС║јт«ъуј░т┐ФжђЪуб░ТњъТБђТхІсђЂУїЃтЏ┤ТЪЦУ»бсђЂТюђУ┐Љжѓ╗Тљюу┤буГЅтіЪУЃйсђѓ тЏЏтЈЅТаЉуџёС╝ўуѓ╣ тЏЏтЈЅТаЉуџёт«ъуј░С╗БуаЂтЁиТюЅС╗ЦСИІС╝ўуѓ╣№╝џ * жФўТЋѕуџётГўтѓетњїТБђу┤бУЃйтіЏ * жФўТЋѕуџёуб░ТњъТБђТхІтњїУїЃтЏ┤ТЪЦУ»бУЃйтіЏ * УЅ»тЦйуџётЈ»ТЅЕт▒ЋТђДтњїуЂхТ┤╗ТђД тЏЏтЈЅТаЉуџёу╝║уѓ╣...
- тѕЮтДІтїќ№╝џтѕЏт╗║СИђСИфуЕ║уџётЏЏтЈЅТаЉ№╝їУ«Йуй«Та╣Уіѓуѓ╣уџёСйЇуй«тњїтцДт░Јсђѓ - ТЈњтЁЦ№╝џт░єСИђСИфуѓ╣ТѕќуЪЕтйбт»╣У▒АТЈњтЁЦтѕ░тЏЏтЈЅТаЉСИГсђѓУ┐ЎжђџтИИТХЅтЈітѕцТќГт»╣У▒АТЅђтюетї║тЪЪ№╝їт╣Хжђњтйњтю░тюеуЏИт║ћтГљУіѓуѓ╣СИГТЈњтЁЦсђѓ - ТЪЦУ»б№╝џТа╣ТЇ«у╗Ўт«џуџёуѓ╣ТѕќуЪЕтйб№╝їТЪЦТЅЙСИјС╣ІуЏИС║цуџё...
5. **жЂЇтјєСИју╗ўтЏЙ**№╝џтЏЏтЈЅТаЉуџётЈ»УДєтїќТў»жђџУ┐ЄGDl+т«ъуј░уџёсђѓGDl+Тў».NET FrameworkуџёСИђжЃетѕє№╝їТЈљСЙЏС║єСИ░т»їуџётЏЙтйбу╗ўтѕХтіЪУЃйсђѓжЂЇтјєтЏЏтЈЅТаЉт╣ХТа╣ТЇ«Уіѓуѓ╣уџёУЙ╣уЋїТАєу╗ўтѕХуЪЕтйб№╝їтЈ»С╗ЦТИЁТЎ░тю░т▒Ћуц║тЏЏтЈЅТаЉуџёу╗ЊТъёсђѓ тюет«ъжЎЁт║ћућеСИГ№╝їтЏЏтЈЅТаЉтИИ...
тюет«ъжЎЁт║ћућеСИГ№╝їтЏЏтЈЅТаЉтЈ»С╗ЦућеТЮЦС╝ўтїќуб░ТњъТБђТхІ№╝їТ»ћтдѓтюеТИИТѕЈтю║ТЎ»СИГ№╝їт┐ФжђЪТЅЙтЄ║СИјТЪљСИђуЅЕСйЊтЈ»УЃйтЈЉућЪуб░Тњъуџёт»╣У▒АсђѓУ┐ўтЈ»С╗ЦућеС║јтю░тЏЙТИ▓ТЪЊ№╝їжђџУ┐Єтѕєт▒ѓтГўтѓетю░уљєС┐АТЂ»№╝їтЈфтіаУййтЈ»УДєУїЃтЏ┤тєЁуџёТЋ░ТЇ«№╝їТЈљжФўТИ▓ТЪЊТЋѕујЄсђѓтюетЏЙтЃЈтцёуљєСИГ№╝їтЏЏтЈЅТаЉ...
тЏЏтЈЅТаЉ№╝ѕQuadtree№╝ЅТў»СИђуДЇТЋ░ТЇ«у╗ЊТъё№╝їт«ЃСИјС║їтЈЅТаЉу▒╗С╝╝№╝їСйєТ»ЈСИфУіѓуѓ╣ТюЅтЏЏСИфтГљУіѓуѓ╣№╝їтѕєтѕФС╗БУАеСИісђЂСИІсђЂтидсђЂтЈ│тЏЏСИфТќ╣тљЉсђѓУ┐ЎуДЇТЋ░ТЇ«у╗ЊТъётюеУ«Ау«ЌТю║уДЉтГдСИГтИИућеС║јтЏЙтЃЈтцёуљєсђЂтю░уљєС┐АТЂ»у│╗у╗ЪсђЂТИИТѕЈу╝ќуеІуГЅжбєтЪЪ№╝їтЏаСИ║т«ЃУЃйтцЪТюЅТЋѕтю░т»╣С║їу╗┤...
тЏЏтЈЅТаЉтѕєтЅ▓Тў»СИђуДЇтюетЏЙтЃЈтцёуљє...Тђ╗уџёТЮЦУ»┤№╝їтЏЏтЈЅТаЉтѕєтЅ▓тюеMATLABСИГуџёт«ъуј░ТХЅтЈітЏЙтЃЈУ»╗тЈќсђЂтЏЏтЈЅТаЉу╗ЊТъёуџёТъёт╗║сђЂУіѓуѓ╣тѕєтЅ▓уГќуЋЦС╗ЦтЈіу╗ЊТъюуџётЈ»УДєтїќсђѓжђџУ┐ЄуљєУДБУ┐ЎС║ЏТдѓт┐хтњїТГЦжфц№╝їСйатЈ»С╗ЦУЄфУАїу╝ќтєЎТѕќС┐«Тћ╣С╗БуаЂ№╝їС╗Цжђѓт║ћСИЇтљїуџётЏЙтЃЈтцёуљєжюђТ▒ѓсђѓ
ТГцтцќ№╝їтЏЏтЈЅТаЉУ┐ўтИИућеС║јуб░ТњъТБђТхІсђЂтЏЙтЃЈтјІу╝ЕсђЂтю░уљєС┐АТЂ»у│╗у╗ЪуГЅ№╝їУЃйтцЪт┐ФжђЪт«џСйЇтњїу╗ёу╗ЄуЕ║жЌ┤тєЁуџётЁЃу┤асђѓ Тђ╗у╗ЊТЮЦУ»┤№╝їтЏЏтЈЅТаЉТў»СИђуДЇтѕєТ▓╗уГќуЋЦуџёТЋ░ТЇ«у╗ЊТъё№╝їжђѓућеС║јС║їу╗┤уЕ║жЌ┤уџёу┤бт╝ЋтњїТЪЦТЅЙС╗╗тіАсђѓт«ЃжђџУ┐ЄСИЇТќГтю░т░єуЕ║жЌ┤тѕњтѕєСИ║тЏЏСИфжЃетѕє№╝ї...
6. **тЈ»УДєтїќ№╝ѕVisualization№╝Ѕ**№╝џСИ║С║єТЏ┤тЦйтю░уљєУДБтњїУ░ЃУ»ЋтЏЏтЈЅТаЉ№╝їтЈ»С╗ЦТЈљСЙЏтЈ»УДєтїќтиЦтЁиТЮЦТўЙуц║ТаЉуџёу╗ЊТъёсђѓ тюе`quadtree-python-main`У┐ЎСИфжА╣уЏ«СИГ№╝їтЈ»УЃйтїЁтљФС║єт«ъуј░У┐ЎС║ЏтіЪУЃйуџёС╗БуаЂсђѓжА╣уЏ«тЈ»УЃйУ┐ўТЈљСЙЏС║єТхІУ»ЋућеСЙІТЮЦжфїУ»ЂтЏЏтЈЅТаЉуџё...