- 浏览: 278719 次
- 性别:

- 来自: 北京
-

文章分类
- 全部博客 (111)
- Ajax (3)
- Oracle (10)
- 云计算 (0)
- Java (10)
- jquery (3)
- 杂 (8)
- 算法导论 (1)
- Flex (3)
- JDBC (1)
- GIS概念 (0)
- CSS (1)
- CVS Eclipse (1)
- Hibernate (1)
- Struts2 (5)
- Servlet JSP (2)
- 数据结构与问题求解 (1)
- CentOS (3)
- C语言名题百则 (4)
- 设计模式 (1)
- Ubuntu (3)
- JavaScript (15)
- C语言 (12)
- 数据结构 (8)
- DOM (4)
- UML (2)
- C语言,C++ (3)
- MongoDB (6)
- 操作系统原理 (6)
- 计算机网络 (0)
- node.js (1)
- FreeBSD (1)
- MySQL (1)
- 通知帖 (0)
- 版本控制 (2)
- Linux (1)
- Vim (1)
- 形式语言与自动机 (0)
- 搜索引擎 (2)
- Haskell (4)
最新评论
-
arther8888:
niedj 写道请问,关于CachedThreadPool的方 ...
Java并发包中的几种ExecutorService -
Lyleluo:
深圳java群 397083120 求职,学习全包,外加小美女 ...
Java数组初始化 -
happyzjj:
楼主讲的很详细,不过关于CachedThreadPool我试的 ...
Java并发包中的几种ExecutorService -
niedj:
请问,关于CachedThreadPool的方式,楼主是否自己 ...
Java并发包中的几种ExecutorService -
garyzhang2681:
2.实现Runnable接口有试过t1.start(); t1 ...
Java多线程笔记1——多线程两种实现方式
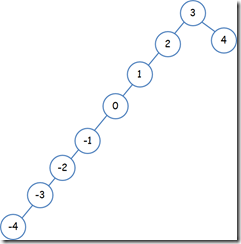
之前学习了二叉查找树的及相关操作。二叉查找树的大部分主要操作的复杂度都是O(logN)量级的。现在考虑这样一种情况:通过集合{3,2,4,1,0,-1,-2,-3,-4,-4}中的元素来构建二叉查找树,得到的树如图所示:
如果现在我们需要查找元素-4,那么时间复杂度还是是O(logN)吗?有个更加极端的例子,假设数据集是{6,5,3,1,0,-1,-2,-3,-4,-4}呢?再去查找元素-4,其复杂度已经是O(N)了。也就是说,二叉查找树的查找优势完全不复存在了。在这样的情况下,以前的牛人们又想出了别的办法:让二叉查找树除了满足现有条件外,添加平衡条件,形成平衡二叉树。AVL树是其中一种典型的平衡二叉树,
AVL树是带有平衡条件的二叉查找树。在满足所有二叉查找树条件下,还加入了平衡条件:AVl树的每个节点的左右子树的高度差必须<=1。 在我使用的这本教材中,定义空树的高度为-1,一个节点的树的高度定义为0。
为了满足平衡条件,AVL树的基本操作一般涉及运作同在不平衡的二叉查找树所运作的同样的算法。但是要进行预先或随后做一次或多次所谓的"AVL旋转"。
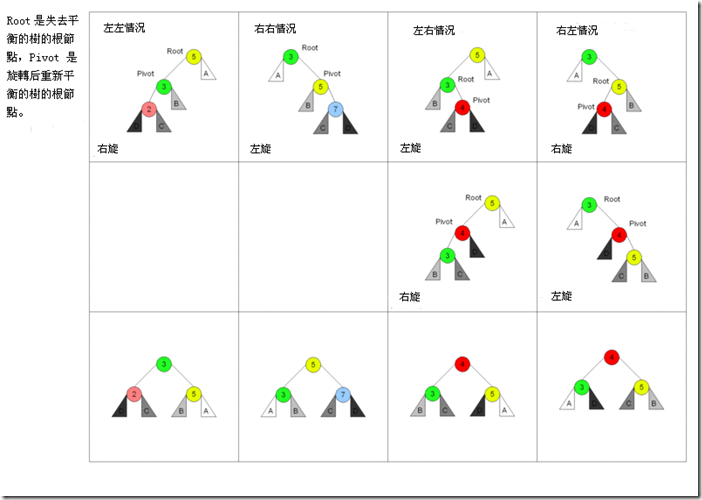
涉及到的几种情况如下图所示:
AVL树的基本操作代码如下:
#include <stdio.h>
#include <stdlib.h>
#define MAX(X,Y) ((X > Y) ? X : Y)
typedef int ElementType;
typedef struct AvlNode *Position;
typedef struct AvlNode *AvlTree;
/************************************************************************/
/* Avl树的数据结构定义以及节本操作定义 */
/************************************************************************/
struct AvlNode
{
ElementType Element;
int Height;
AvlTree Left,Right;
};
AvlTree MakeEmpty(AvlTree T); /*清空Avl树*/
Position Find(ElementType X, AvlTree T); /*在Avl树中查找指定的元素*/
Position FindMax(AvlTree T); /*在Avl树中查找最大元素*/
Position FindMin(AvlTree T); /*在Avl树中查找最小元素*/
AvlTree Insert(ElementType X, AvlTree T); /*在Avl树中插入指定元素*/
AvlTree Delete(ElementType X, AvlTree T); /*在Avl树中删除指定元素*/
ElementType Retrieve(Position P); /*获取指定节点的元素值*/
int Height(Position P); /*获得指定节点的高度值*/
Position SingleRotateWithLeft(Position P); /*单右旋转*/
Position SingleRotateWithRight(Position P); /*单左旋转*/
Position DoubleRotateWithLeft(Position P); /*双左右旋转*/
Position DoubleRotateWithRight(Position P); /*双右左旋转*/
int main(void)
{
return 0;
}
/************************************************************************/
/* 清空AVL树的操作与清空普通二叉树相同 */
/************************************************************************/
AvlTree MakeEmpty(AvlTree T)
{
if (!T)
{
MakeEmpty(T->Left);
MakeEmpty(T->Right);
free(T);
}
return NULL;
}
/************************************************************************/
/*在Avl树中查找指定的元素,与二叉查找树的操作相同 */
/************************************************************************/
Position Find(ElementType X, AvlTree T)
{
if (T == NULL)
{
return NULL;
}
else
{
if (X < T->Element)
{
return Find(X,T->Left);
}
else if(X > T->Element)
{
return Find(X, T->Right);
}
else
{
return T;
}
}
}
/************************************************************************/
/* 在Avl树中查找最大值(递归写法) */
/************************************************************************/
Position FindMax(AvlTree T)
{
if (T == NULL)
{
return NULL;
}
else
{
if (T->Right == NULL)
{
return NULL;
}
else
{
return FindMax(T->Right);
}
}
}
/************************************************************************/
/* 在Avl树中查找最小值(非递归写法) */
/************************************************************************/
Position FindMin(AvlTree T)
{
if (T == NULL)
{
return NULL;
}
else
{
while (T->Left != NULL)
{
T = T->Left;
}
return T;
}
}
/************************************************************************/
/* 返回指定节点的高度信息 */
/************************************************************************/
int Height(Position P)
{
if (P == NULL)
{
return -1;
}
else
{
return P->Height;
}
}
/************************************************************************/
/* 单旋转:右旋转 */
/* 使用条件:这个函数只适合当P有左子树时调用; */
/* 作用:在P和其左子树根节点之间执行一次单右旋转 */
/************************************************************************/
Position SingleRotateWithLeft(Position P)
{
Position LChild = P->Left;
P->Left = LChild->Right; /*将P的左孩子设置成LChild的右孩子*/
LChild->Right = P;
P->Height = MAX(Height(P->Left),Height(P->Right)) + 1;/*更新高度信息*/
LChild->Height = MAX(Height(LChild->Left),P->Height) + 1;
return LChild; /*新的根节点*/
}
/************************************************************************/
/* 单旋转:左旋转 */
/* 使用条件:这个函数只适合当P有右子树时调用; */
/* 作用:在P和其右子树根节点之间执行一次单左旋转 */
/************************************************************************/
Position SingleRotateWithRight(Position P)
{
Position RChild = P->Right; /*将P的右孩子设置成RChild的右孩子*/
P->Right = RChild->Left;
RChild->Left = P;
P->Height = MAX(Height(P->Left),Height(P->Right)) + 1;/*更新高度信息*/
RChild->Height = MAX(Height(RChild->Right),P->Height) + 1;
return RChild; /*新的根节点*/
}
/************************************************************************/
/* 双旋转:左右旋转 */
/* 使用条件:适合于当P有左孩子,而左孩子有右孩子 */
/* 作用:*/
/************************************************************************/
Position DoubleRotateWithLeft(Position P)
{
P->Left = SingleRotateWithRight(P->Left); /*先进行左旋转*/
return SingleRotateWithLeft(P); /*再进行又旋转*/
}
/************************************************************************/
/* 双旋转:右左旋转 */
/* 使用条件:适合于当P有右孩子,而右孩子有左孩子 */
/* 作用:*/
/************************************************************************/
Position DoubleRotateWithRight(Position P)
{
P->Right = SingleRotateWithLeft(P->Right); /*先进行右旋转*/
return SingleRotateWithRight(P); /*再进行左旋转*/
}
/************************************************************************/
/* AVL树插入操作 */
/************************************************************************/
AvlTree Insert(ElementType X, AvlTree T)
{
/*如果T是一棵空树,那么创建一个节点作为树的根节点*/
if (T == NULL)
{
T = malloc(sizeof(struct AvlNode));
if(T == NULL)
{
fprintf(stderr,"Out of space!");
}
else
{
T->Element = X;
T->Left = NULL;
T->Right = NULL;
T->Height = 0;
}
}else
{
if (X < T->Element)
{
T->Left = Insert(X,T->Left);
/*判断是否打破了破了平衡条件*/
if (Height(T->Left) - Height(T->Right) == 2)
{
/*判断是四种情况中的哪一种情况*/
if (X < T->Left->Element)
{
T = SingleRotateWithLeft(T);
}
else if (X > T->Left->Element)
{
T = DoubleRotateWithLeft(T);
}
}
}
else if (X > T->Element)
{
T->Right = Insert(X,T->Right);
if (Height(T->Right) - Height(T->Left) == 2)
{
if(X < T->Right->Element)
{
T = DoubleRotateWithRight(T);
}
else if (X > T->Right->Element)
{
T = SingleRotateWithRight(T);
}
}
}
else
{
/*元素已经存在于AVL树中,因此不需要再做别的工作*/
}
/*更新数的高度信息*/
T->Height = MAX(Height(T->Left),Height(T->Right)) + 1;
}
return T;
}
发表评论
-
等值首尾和问题
2011-12-24 00:03 747问题:假设有一个数组x[],有n个元素,并且每一个都大于零;称 ... -
两数组最小距离问题
2011-12-11 23:26 3301已知两个元素从小到大排列的数组x[]和y[], ... -
等值数目问题
2011-11-27 00:44 737问题描述:已知两个整型数组f[]和g[],它们的元素都已经从小 ... -
重学数据结构007——二叉查找树
2011-11-22 21:36 1750之前的博客中提到过,我学习采用 ... -
重学数据结构006——中缀表达式转后缀表达式
2011-11-18 21:38 3257我们在数学中常见的计算式,例如2+(3*4)叫 ... -
重学数据结构005——栈的应用之平衡符号
2011-11-18 12:01 2375之前学习了栈的基本操作,并且学习了栈 ... -
重学数据结构004——栈的基本操作及实现(数组实现)
2011-11-17 23:13 1452上文提到过栈以及栈的基本操作。上文中是基于链表做的实现 ... -
重学数据结构003——栈的基本操作及实现(链式存储)
2011-11-14 23:19 19671.栈的概念 展示只允许在其一端进行插入语删除操 ... -
重学数据结构002——桶排序、基数排序
2011-11-11 17:17 20781.桶排序 � ... -
重学数据结构001——链表基本操作与一元多项式相加(C语言)
2011-11-10 13:26 5298大一的时候我们专业开了一门C语言限选课,老师觉 ... -
在MacOS Lion上编译GCC4.6.1
2011-10-28 13:15 0翻译文章,原文地址:h ... -
C语言中指针的操作
2011-10-23 00:27 2472C语言中指针操作主要有以下几种: 指针赋值(assignm ...






相关推荐
【AVL搜索树详解】 ...总之,AVL搜索树是一种高效的数据结构,适用于需要快速查找、插入和删除操作的应用场景。通过理解AVL树的原理和操作,开发者可以灵活地应用这种数据结构解决实际问题,提升算法性能。
本实验专注于二叉查找树(Binary Search Tree, BST)以及它的平衡版本——AVL树。这两种数据结构在处理大量数据时,尤其是进行查找、插入和删除操作时,具有较高的效率。 首先,二叉查找树是一种特殊的二叉树,其中...
2. **AVL树的旋转操作**:分为四种类型——左旋、右旋、左右旋和右左旋,用于在插入和删除后恢复树的平衡。例如,当一个节点的左子树过高(高度差大于1),可能需要进行右旋;反之,如果右子树过高,则可能需要左旋...
"数据结构——树结构.ppt"这份文件很显然是一个关于树结构的讲座或教程材料,它可能涵盖了树的基本概念、算法实现以及实际应用。 首先,我们要理解树的基本概念。树是一种非线性的数据结构,由若干个节点(或称为...
本实验“广工数据结构实验——平衡二叉树”着重探讨了一种特殊类型的数据结构,即平衡二叉树。平衡二叉树是二叉搜索树(Binary Search Tree, BST)的一个变体,它通过保持树的高度平衡来确保查找、插入和删除操作的...
在本实验“数据结构实验——树和二叉树子系统”中,我们将深入理解二叉树的特性和操作。 首先,实验目的主要涵盖以下几个方面: 1. **理解二叉树特点**:二叉树的每个节点至多有两个子节点,它允许快速查找、插入...
在本实验“数据结构实验——查找算法的实现”中,主要关注的是数据结构中的查找算法,特别是二叉排序树和平衡二叉树的构建、查找、插入和删除操作。实验目的是通过实际操作来理解并比较不同查找算法的性能,如平均...
《数据结构——C++实现》(第二版)是一本经典的计算机科学教材,专注于介绍各种数据结构及其在C++编程语言中的实现。这本书的核心是通过实际的代码示例帮助读者理解和掌握数据结构的基本概念,这对于任何想要深入...
5. **树**:一种分层数据结构,包括二叉树、平衡二叉树(如AVL树和红黑树)、B树、B+树等。课件会讲解树的遍历算法和查找、插入、删除操作。 6. **图**:用于表示对象之间的关系,有无向图、有向图、加权图等。图的...
常见的数据结构包括数组、链表、栈、队列、树(如二叉树、AVL树、红黑树等)、图以及哈希表等。了解这些数据结构的特性及其适用场景,是提升编程能力的关键。 算法是解决问题或执行任务的精确步骤序列。在数据结构...
树是一种非线性的数据结构,由节点和边构成,每个节点可以有零个或多个子节点。二叉树是最简单的一种,每个节点最多有两个子节点。二叉搜索树(BST)是一种特殊的二叉树,其中每个节点的左子树只包含小于该节点的...
《数据结构——使用C语言(第4版)》是由朱战立编著的一本经典教材,旨在帮助读者理解和掌握数据结构的基本概念及其在C语言中的实现。本书通过实例和讲解,使学习者能够运用C语言来设计和实现各种数据结构。 在...
这份“数据结构习题集——目前最完整的数据结构1800题包括完整答案”提供了丰富的练习题目和解答,旨在帮助学习者深入理解和掌握数据结构的基本概念、算法和应用。 首先,我们要理解数据结构的概念。数据结构是数据...
特别是对于需要高度动态性和平衡性的应用,如数据库和文件系统,一种特殊的二叉搜索树——AVL树,是非常重要的。AVL树是由俄罗斯数学家G.M. Adelson-Velsky和E.M. Landis在1962年首次提出的,因此被命名为AVL树。...
在这个“数据结构实验——停车场程序”的主题中,我们主要关注的是如何运用数据结构来模拟现实世界中的停车场系统。 首先,停车场程序的核心在于如何组织和管理车位的信息。在设计数据结构时,我们可以考虑以下几点...
"数据结构课程设计——树的遍历"这一主题聚焦于树这种非线性数据结构的一个核心操作:遍历。两江大学出版社可能提供了深入的教程或实践项目,让学生通过实际操作来理解和掌握树的遍历方法。 树是一种由节点(也称为...
1、该资源内项目代码都经过测试运行成功,功能ok的情况下才上传的,请放心下载使用! 2、本项目适合计算机相关专业(如计科、人工智能、通信工程、自动化、电子信息等)的在校学生、老师或者企业员工下载使用,也适合...
本教程“数据结构算法——Visual C++6.0程序集”很可能是通过C++语言来阐述数据结构和算法的实现。 数据结构主要包括数组、链表、栈、队列、树、图、哈希表等多种类型。数组是最基本的数据结构,它提供了通过索引...
本资料包"数据结构教案——PPT与程序代码"提供了第四版课程的详细教学资源,包括PPT演示文稿和实际编程代码,非常适合学习者或教师使用。 首先,PPT部分通常会涵盖以下关键知识点: 1. **数组**:基础数据结构,...
Python实现的AVL树则是用Python语言编写的数据结构,它保持了树的平衡状态,使得基本的动态集合操作如查找、插入、删除的时间复杂度都是O(log n),从而克服了普通的二叉搜索树在最坏情况下可能退化成链表,导致操作...