第дәҢйғЁеҲҶгҖҒиҙқеҸ¶ж–ҜеҲҶзұ»
жҳ”дәәе·Ід№ҳй»„й№ӨеҺ»пјҢжӯӨең°з©әдҪҷй»„й№ӨжҘјпјӣй»„й№ӨдёҖеҺ»дёҚеӨҚиҝ”пјҢзҷҪдә‘еҚғиҪҪз©әжӮ жӮ гҖӮ
В В еҗҺдҫҝеӨ§дёәжҠҳжңҚпјҢе·Іж— д»Җе…ҙиҮҙеҶҚжҸҗдәҶ(еҒ¶зҺ°еңЁе°ұжҳҜиҝҷж„ҹи§ү)пјҢ然ж–Үз« иҝҳеҫ—继з»ӯеҶҷгҖӮSoпјҢжң¬ж–Ү第дәҢйғЁеҲҶд№ӢеӨ§йғЁеҲҶеҹәжң¬ж•ҙзҗҶиҮӘжңӘй№Ҹе…„д№ӢжүӢ(еҒҡдәҶйғЁеҲҶж”№еҠЁ)пјҢиӢҘжңүд»»дҪ•дёҚеҰҘд№ӢеӨ„пјҢиҝҳжңӣиҜ»иҖ…е’ҢжңӘй№Ҹе…„жө·ж¶өпјҢи°ўи°ўгҖӮ
2.1гҖҒд»Җд№ҲжҳҜиҙқеҸ¶ж–ҜеҲҶзұ»
- P(A)жҳҜAзҡ„е…ҲйӘҢжҰӮзҺҮжҲ–иҫ№зјҳжҰӮзҺҮгҖӮд№ӢжүҖд»Ҙз§°дёә"е…ҲйӘҢ"жҳҜеӣ зӮәе®ғдёҚиҖғиҷ‘д»»дҪ•Bж–№йқўзҡ„еӣ зҙ гҖӮ
- P(A|B)жҳҜе·ІзҹҘBеҸ‘з”ҹеҗҺAзҡ„жқЎд»¶жҰӮзҺҮпјҲзӣҙзҷҪжқҘи®ІпјҢе°ұжҳҜе…ҲжңүBиҖҢеҗҺ=>жүҚжңүAпјүпјҢд№ҹз”ұдәҺеҫ—иҮӘBзҡ„еҸ–еҖјиҖҢиў«з§°дҪңAзҡ„еҗҺйӘҢжҰӮзҺҮгҖӮ
- P(B|A)жҳҜе·ІзҹҘAеҸ‘з”ҹеҗҺBзҡ„жқЎд»¶жҰӮзҺҮпјҲзӣҙзҷҪжқҘи®ІпјҢе°ұжҳҜе…ҲжңүAиҖҢеҗҺ=>жүҚжңүBпјүпјҢд№ҹз”ұдәҺеҫ—иҮӘAзҡ„еҸ–еҖјиҖҢиў«з§°дҪңBзҡ„еҗҺйӘҢжҰӮзҺҮгҖӮ
- P(B)жҳҜBзҡ„е…ҲйӘҢжҰӮзҺҮжҲ–иҫ№зјҳжҰӮзҺҮпјҢд№ҹдҪңж ҮеҮҶеҢ–еёёйҮҸпјҲnormalizedВ constantпјүгҖӮ
2.2В иҙқеҸ¶ж–Ҝе…¬ејҸеҰӮдҪ•иҖҢжқҘ
В В иҙқеҸ¶ж–Ҝе…¬ејҸжҳҜжҖҺд№ҲжқҘзҡ„пјҹдёӢйқўеҶҚдёҫwikipedia дёҠзҡ„дёҖдёӘдҫӢеӯҗпјҡ
дёҖжүҖеӯҰж ЎйҮҢйқўжңү 60% зҡ„з”·з”ҹпјҢ40% зҡ„еҘіз”ҹгҖӮз”·з”ҹжҖ»жҳҜз©ҝй•ҝиЈӨпјҢеҘіз”ҹеҲҷдёҖеҚҠз©ҝй•ҝиЈӨдёҖеҚҠз©ҝиЈҷеӯҗгҖӮжңүдәҶиҝҷдәӣдҝЎжҒҜд№ӢеҗҺжҲ‘们еҸҜд»Ҙе®№жҳ“ең°и®Ўз®—вҖңйҡҸжңәйҖүеҸ–дёҖдёӘеӯҰз”ҹпјҢд»–пјҲеҘ№пјүз©ҝй•ҝиЈӨзҡ„жҰӮзҺҮе’Ңз©ҝиЈҷеӯҗзҡ„жҰӮзҺҮжҳҜеӨҡеӨ§вҖқпјҢиҝҷдёӘе°ұжҳҜеүҚйқўиҜҙзҡ„вҖңжӯЈеҗ‘жҰӮзҺҮвҖқзҡ„и®Ўз®—гҖӮ然иҖҢпјҢеҒҮи®ҫдҪ иө°еңЁж ЎеӣӯдёӯпјҢиҝҺйқўиө°жқҘдёҖдёӘз©ҝй•ҝиЈӨзҡ„еӯҰз”ҹпјҲеҫҲдёҚе№ёзҡ„жҳҜдҪ й«ҳеәҰиҝ‘дјјпјҢдҪ еҸӘзңӢеҫ—и§Ғд»–пјҲеҘ№пјүз©ҝзҡ„жҳҜеҗҰй•ҝиЈӨпјҢиҖҢж— жі•зЎ®е®ҡд»–пјҲеҘ№пјүзҡ„жҖ§еҲ«пјүпјҢдҪ иғҪеӨҹжҺЁж–ӯеҮәд»–пјҲеҘ№пјүжҳҜз”·з”ҹзҡ„жҰӮзҺҮжҳҜеӨҡеӨ§еҗ—пјҹ
В В дёҖдәӣи®ӨзҹҘ科еӯҰзҡ„з ”з©¶иЎЁжҳҺпјҲгҖҠеҶізӯ–дёҺеҲӨж–ӯгҖӢд»ҘеҸҠгҖҠRationality for MortalsгҖӢ第12з« пјҡе°Ҹеӯ©д№ҹеҸҜд»Ҙи§ЈеҶіиҙқеҸ¶ж–Ҝй—®йўҳпјүпјҢжҲ‘们еҜ№еҪўејҸеҢ–зҡ„иҙқеҸ¶ж–Ҝй—®йўҳдёҚж“…й•ҝпјҢдҪҶеҜ№дәҺд»Ҙйў‘зҺҮеҪўејҸе‘ҲзҺ°зҡ„зӯүд»·й—®йўҳеҚҙеҫҲж“…й•ҝгҖӮеңЁиҝҷйҮҢпјҢжҲ‘们дёҚеҰЁжҠҠй—®йўҳйҮҚж–°еҸҷиҝ°жҲҗпјҡдҪ еңЁж ЎеӣӯйҮҢйқўйҡҸжңәжёёиө°пјҢйҒҮеҲ°дәҶ N дёӘз©ҝй•ҝиЈӨзҡ„дәәпјҲд»Қ然еҒҮи®ҫдҪ ж— жі•зӣҙжҺҘи§ӮеҜҹеҲ°д»–们зҡ„жҖ§еҲ«пјүпјҢй—®иҝҷ N дёӘдәәйҮҢйқўжңүеӨҡе°‘дёӘеҘіз”ҹеӨҡе°‘дёӘз”·з”ҹгҖӮ
В В дҪ иҜҙпјҢиҝҷиҝҳдёҚз®ҖеҚ•пјҡз®—еҮәеӯҰж ЎйҮҢйқўжңүеӨҡе°‘з©ҝй•ҝиЈӨзҡ„пјҢ然еҗҺеңЁиҝҷдәӣдәәйҮҢйқўеҶҚз®—еҮәжңүеӨҡе°‘еҘіз”ҹпјҢдёҚе°ұиЎҢдәҶпјҹ
В В жҲ‘们жқҘз®—дёҖз®—пјҡеҒҮи®ҫеӯҰж ЎйҮҢйқўдәәзҡ„жҖ»ж•°жҳҜ U дёӘгҖӮ60% зҡ„з”·з”ҹйғҪз©ҝй•ҝиЈӨпјҢдәҺжҳҜжҲ‘们еҫ—еҲ°дәҶ U * P(Boy) * P(Pants|Boy) дёӘз©ҝй•ҝиЈӨзҡ„пјҲз”·з”ҹпјүпјҲе…¶дёӯ P(Boy) жҳҜз”·з”ҹзҡ„жҰӮзҺҮ = 60%пјҢиҝҷйҮҢеҸҜд»Ҙз®ҖеҚ•зҡ„зҗҶи§Јдёәз”·з”ҹзҡ„жҜ”дҫӢпјӣP(Pants|Boy) жҳҜжқЎд»¶жҰӮзҺҮпјҢеҚіеңЁ Boy иҝҷдёӘжқЎд»¶дёӢз©ҝй•ҝиЈӨзҡ„жҰӮзҺҮжҳҜеӨҡеӨ§пјҢиҝҷйҮҢжҳҜ 100% пјҢеӣ дёәжүҖжңүз”·з”ҹйғҪз©ҝй•ҝиЈӨпјүгҖӮ40% зҡ„еҘіз”ҹйҮҢйқўеҸҲжңүдёҖеҚҠпјҲ50%пјүжҳҜз©ҝй•ҝиЈӨзҡ„пјҢдәҺжҳҜжҲ‘们еҸҲеҫ—еҲ°дәҶ U * P(Girl) * P(Pants|Girl) дёӘз©ҝй•ҝиЈӨзҡ„пјҲеҘіз”ҹпјүгҖӮеҠ иө·жқҘдёҖе…ұжҳҜ U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl) дёӘз©ҝй•ҝиЈӨзҡ„пјҢе…¶дёӯжңү U * P(Girl) * P(Pants|Girl) дёӘеҘіз”ҹгҖӮдёӨиҖ…дёҖжҜ”е°ұжҳҜдҪ иҰҒжұӮзҡ„зӯ”жЎҲгҖӮ
В В дёӢйқўжҲ‘们жҠҠиҝҷдёӘзӯ”жЎҲеҪўејҸеҢ–дёҖдёӢпјҡжҲ‘们иҰҒжұӮзҡ„жҳҜ P(Girl|Pants) пјҲз©ҝй•ҝиЈӨзҡ„дәәйҮҢйқўжңүеӨҡе°‘еҘіз”ҹпјүпјҢжҲ‘们计算зҡ„з»“жһңжҳҜ U * P(Girl) * P(Pants|Girl) / [U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl)] гҖӮе®№жҳ“еҸ‘зҺ°иҝҷйҮҢж ЎеӣӯеҶ…дәәзҡ„жҖ»ж•°жҳҜж— е…ізҡ„пјҢдёӨиҫ№еҗҢж—¶ж¶ҲеҺ»UпјҢдәҺжҳҜеҫ—еҲ°
В
P(Girl|Pants) = P(Girl) * P(Pants|Girl) / [P(Boy) * P(Pants|Boy) + P(Girl) * P(Pants|Girl)]
В
В В жіЁж„ҸпјҢеҰӮжһңжҠҠдёҠејҸ收缩иө·жқҘпјҢеҲҶжҜҚе…¶е®һе°ұжҳҜ P(Pants) пјҢеҲҶеӯҗе…¶е®һе°ұжҳҜ P(Pants, Girl) гҖӮиҖҢиҝҷдёӘжҜ”дҫӢеҫҲиҮӘ然ең°е°ұиҜ»дҪңпјҡеңЁз©ҝй•ҝиЈӨзҡ„дәәпјҲ P(Pants) пјүйҮҢйқўжңүеӨҡе°‘пјҲз©ҝй•ҝиЈӨпјүзҡ„еҘіеӯ©пјҲ P(Pants, Girl) пјүгҖӮ
В В дёҠејҸдёӯзҡ„ Pants е’Ң Boy/Girl еҸҜд»ҘжҢҮд»ЈдёҖеҲҮдёңиҘҝпјҢSoпјҢе…¶дёҖиҲ¬еҪўејҸе°ұжҳҜпјҡ
P(B|A) = P(A|B) * P(B) / [P(A|B) * P(B) + P(A|~B) * P(~B) ]
  收缩иө·жқҘе°ұжҳҜпјҡ
P(B|A) = P(AB) / P(A)
В В е…¶е®һиҝҷдёӘе°ұзӯүдәҺпјҡ
P(B|A) * P(A) = P(AB)
В В жӣҙиҝӣдёҖжӯҘйҳҗиҝ°пјҢP(B|A)дҫҝжҳҜеңЁжқЎд»¶Aзҡ„жғ…еҶөдёӢпјҢBеҮәзҺ°зҡ„жҰӮзҺҮжҳҜеӨҡеӨ§гҖӮ然зңӢдјјиҝҷд№Ҳе№іеҮЎзҡ„иҙқеҸ¶ж–Ҝе…¬ејҸпјҢиғҢеҗҺеҚҙйҡҗеҗ«зқҖйқһеёёж·ұеҲ»зҡ„еҺҹзҗҶгҖӮ
2.3гҖҒжӢјеҶҷзә жӯЈ
В В В з»Ҹе…ёи‘—дҪңгҖҠдәәе·ҘжҷәиғҪпјҡзҺ°д»Јж–№жі•гҖӢзҡ„дҪңиҖ…д№ӢдёҖ Peter Norvig жӣҫз»ҸеҶҷиҝҮдёҖзҜҮд»Ӣз»ҚеҰӮдҪ•еҶҷдёҖдёӘжӢјеҶҷжЈҖжҹҘ/зә жӯЈеҷЁзҡ„ж–Үз« пјҢйҮҢйқўз”ЁеҲ°зҡ„е°ұжҳҜиҙқеҸ¶ж–Ҝж–№жі•пјҢдёӢйқўпјҢе°Ҷе…¶ж ёеҝғжҖқжғіз®ҖеҚ•жҸҸиҝ°дёӢгҖӮ
В В В йҰ–е…ҲпјҢжҲ‘们йңҖиҰҒиҜўй—®зҡ„жҳҜпјҡвҖңй—®йўҳжҳҜд»Җд№ҲпјҹвҖқ
В В В й—®йўҳжҳҜжҲ‘们зңӢеҲ°з”ЁжҲ·иҫ“е…ҘдәҶдёҖдёӘдёҚеңЁеӯ—е…ёдёӯзҡ„еҚ•иҜҚпјҢжҲ‘们йңҖиҰҒеҺ»зҢңжөӢпјҡвҖңиҝҷдёӘ家дјҷеҲ°еә•зңҹжӯЈжғіиҫ“е…Ҙзҡ„еҚ•иҜҚжҳҜд»Җд№Ҳе‘ўпјҹвҖқз”ЁеҲҡжүҚжҲ‘们еҪўејҸеҢ–зҡ„иҜӯиЁҖжқҘеҸҷиҝ°е°ұжҳҜпјҢжҲ‘们йңҖиҰҒжұӮпјҡ
P(жҲ‘们зҢңжөӢд»–жғіиҫ“е…Ҙзҡ„еҚ•иҜҚ | д»–е®һйҷ…иҫ“е…Ҙзҡ„еҚ•иҜҚ)
В В В иҝҷдёӘжҰӮзҺҮгҖӮ并жүҫеҮәйӮЈдёӘдҪҝеҫ—иҝҷдёӘжҰӮзҺҮжңҖеӨ§зҡ„зҢңжөӢеҚ•иҜҚгҖӮжҳҫ然пјҢжҲ‘们зҡ„зҢңжөӢжңӘеҝ…жҳҜе”ҜдёҖзҡ„пјҢе°ұеғҸеүҚйқўдёҫзҡ„йӮЈдёӘиҮӘ然иҜӯиЁҖзҡ„жӯ§д№үжҖ§зҡ„дҫӢеӯҗдёҖж ·пјӣиҝҷйҮҢпјҢжҜ”еҰӮз”ЁжҲ·иҫ“е…Ҙпјҡ thew пјҢйӮЈд№Ҳд»–еҲ°еә•жҳҜжғіиҫ“е…Ҙ the пјҢиҝҳжҳҜжғіиҫ“е…Ҙ thaw пјҹеҲ°еә•е“ӘдёӘзҢңжөӢеҸҜиғҪжҖ§жӣҙеӨ§е‘ўпјҹе№ёиҝҗзҡ„жҳҜжҲ‘们еҸҜд»Ҙз”ЁиҙқеҸ¶ж–Ҝе…¬ејҸжқҘзӣҙжҺҘеҮәе®ғ们еҗ„иҮӘзҡ„жҰӮзҺҮпјҢжҲ‘们дёҚеҰЁе°ҶжҲ‘们зҡ„еӨҡдёӘзҢңжөӢи®°дёә h1 h2 .. пјҲ h д»ЈиЎЁ hypothesisпјүпјҢе®ғ们йғҪеұһдәҺдёҖдёӘжңүйҷҗдё”зҰ»ж•Јзҡ„зҢңжөӢз©әй—ҙ H пјҲеҚ•иҜҚжҖ»е…ұе°ұйӮЈд№ҲеӨҡиҖҢе·ІпјүпјҢе°Ҷз”ЁжҲ·е®һйҷ…иҫ“е…Ҙзҡ„еҚ•иҜҚи®°дёә D пјҲ D д»ЈиЎЁ Data пјҢеҚіи§ӮжөӢж•°жҚ®пјүпјҢдәҺжҳҜ
P(жҲ‘们зҡ„зҢңжөӢ1 | д»–е®һйҷ…иҫ“е…Ҙзҡ„еҚ•иҜҚ)
В В В еҸҜд»ҘжҠҪиұЎең°и®°дёәпјҡ
P(h1 | D)
В В В зұ»дјјең°пјҢеҜ№дәҺжҲ‘们зҡ„зҢңжөӢ2пјҢеҲҷжҳҜ P(h2 | D)гҖӮдёҚеҰЁз»ҹдёҖи®°дёәпјҡ
P(h | D)
иҝҗз”ЁдёҖж¬ЎиҙқеҸ¶ж–Ҝе…¬ејҸпјҢжҲ‘们еҫ—еҲ°пјҡ
P(h | D) = P(h) * P(D | h) / P(D)
В В В еҜ№дәҺдёҚеҗҢзҡ„е…·дҪ“зҢңжөӢ h1 h2 h3 .. пјҢP(D) йғҪжҳҜдёҖж ·зҡ„пјҢжүҖд»ҘеңЁжҜ”иҫғ P(h1 | D) е’Ң P(h2 | D) зҡ„ж—¶еҖҷжҲ‘们еҸҜд»ҘеҝҪз•ҘиҝҷдёӘеёёж•°гҖӮеҚіжҲ‘们еҸӘйңҖиҰҒзҹҘйҒ“пјҡ
P(h | D) вҲқ P(h) * P(D | h) пјҲжіЁпјҡйӮЈдёӘз¬ҰеҸ·зҡ„ж„ҸжҖқжҳҜвҖңжӯЈжҜ”дҫӢдәҺвҖқпјҢдёҚжҳҜж— з©·еӨ§пјҢжіЁж„Ҹз¬ҰеҸ·еҸіз«ҜжҳҜжңүдёҖдёӘе°ҸзјәеҸЈзҡ„гҖӮпјү
В В В иҝҷдёӘејҸеӯҗзҡ„жҠҪиұЎеҗ«д№үжҳҜпјҡеҜ№дәҺз»ҷе®ҡи§ӮжөӢж•°жҚ®пјҢдёҖдёӘзҢңжөӢжҳҜеҘҪжҳҜеқҸпјҢеҸ–еҶідәҺвҖңиҝҷдёӘзҢңжөӢжң¬иә«зӢ¬з«Ӣзҡ„еҸҜиғҪжҖ§еӨ§е°ҸпјҲе…ҲйӘҢжҰӮзҺҮпјҢPrior пјүвҖқе’ҢвҖңиҝҷдёӘзҢңжөӢз”ҹжҲҗжҲ‘们и§ӮжөӢеҲ°зҡ„ж•°жҚ®зҡ„еҸҜиғҪжҖ§еӨ§е°ҸвҖқпјҲ似然пјҢLikelihood пјүзҡ„д№ҳз§ҜгҖӮе…·дҪ“еҲ°жҲ‘们зҡ„йӮЈдёӘ thew дҫӢеӯҗдёҠпјҢеҗ«д№үе°ұжҳҜпјҢз”ЁжҲ·е®һйҷ…жҳҜжғіиҫ“е…Ҙ the зҡ„еҸҜиғҪжҖ§еӨ§е°ҸеҸ–еҶідәҺ the жң¬иә«еңЁиҜҚжұҮиЎЁдёӯиў«дҪҝз”Ёзҡ„еҸҜиғҪжҖ§пјҲйў‘з№ҒзЁӢеәҰпјүеӨ§е°ҸпјҲе…ҲйӘҢжҰӮзҺҮпјүе’Ң жғіжү“ the еҚҙжү“жҲҗ thew зҡ„еҸҜиғҪжҖ§еӨ§е°ҸпјҲ似然пјүзҡ„д№ҳз§ҜгҖӮ
В В В еү©дёӢзҡ„дәӢжғ…е°ұеҫҲз®ҖеҚ•дәҶпјҢеҜ№дәҺжҲ‘们зҢңжөӢдёәеҸҜиғҪзҡ„жҜҸдёӘеҚ•иҜҚи®Ўз®—дёҖдёӢ P(h) * P(D | h) иҝҷдёӘеҖјпјҢ然еҗҺеҸ–жңҖеӨ§зҡ„пјҢеҫ—еҲ°зҡ„е°ұжҳҜжңҖйқ и°ұзҡ„зҢңжөӢгҖӮжӣҙеӨҡз»ҶиҠӮиҜ·еҸӮзңӢжңӘй№Ҹе…„д№ӢеҺҹж–ҮгҖӮ
2.4гҖҒиҙқеҸ¶ж–Ҝзҡ„еә”з”Ё
2.4.1гҖҒдёӯж–ҮеҲҶиҜҚ
В
В В иҙқеҸ¶ж–ҜжҳҜжңәеҷЁеӯҰд№ зҡ„ж ёеҝғж–№жі•д№ӢдёҖгҖӮжҜ”еҰӮдёӯж–ҮеҲҶиҜҚйўҶеҹҹе°ұз”ЁеҲ°дәҶиҙқеҸ¶ж–ҜгҖӮжөӘжҪ®д№Ӣе·…зҡ„дҪңиҖ…еҗҙеҶӣеңЁгҖҠж•°еӯҰд№ӢзҫҺгҖӢзі»еҲ—дёӯе°ұжңүдёҖзҜҮжҳҜд»Ӣз»Қдёӯж–ҮеҲҶиҜҚзҡ„гҖӮиҝҷйҮҢд»Ӣз»ҚдёҖдёӢж ёеҝғзҡ„жҖқжғіпјҢдёҚеҒҡиөҳиҝ°пјҢиҜҰз»ҶиҜ·еҸӮиҖғеҗҙеҶӣзҡ„еҺҹж–ҮгҖӮ
В В еҲҶиҜҚй—®йўҳзҡ„жҸҸиҝ°дёәпјҡз»ҷе®ҡдёҖдёӘеҸҘеӯҗпјҲеӯ—дёІпјүпјҢеҰӮпјҡ
В В В еҚ—дә¬еёӮй•ҝжұҹеӨ§жЎҘ
В В еҰӮдҪ•еҜ№иҝҷдёӘеҸҘеӯҗиҝӣиЎҢеҲҶиҜҚпјҲиҜҚдёІпјүжүҚжҳҜжңҖйқ и°ұзҡ„гҖӮдҫӢеҰӮпјҡ
1. еҚ—дә¬еёӮ/й•ҝжұҹеӨ§жЎҘ
2. еҚ—дә¬/еёӮй•ҝ/жұҹеӨ§жЎҘ
В
В В иҝҷдёӨдёӘеҲҶиҜҚпјҢеҲ°еә•е“ӘдёӘжӣҙйқ и°ұе‘ўпјҹ
В В жҲ‘们用иҙқеҸ¶ж–Ҝе…¬ејҸжқҘеҪўејҸеҢ–ең°жҸҸиҝ°иҝҷдёӘй—®йўҳпјҢд»Ө X дёәеӯ—дёІпјҲеҸҘеӯҗпјүпјҢY дёәиҜҚдёІпјҲдёҖз§Қзү№е®ҡзҡ„еҲҶиҜҚеҒҮи®ҫпјүгҖӮжҲ‘们е°ұжҳҜйңҖиҰҒеҜ»жүҫдҪҝеҫ— P(Y|X) жңҖеӨ§зҡ„ Y пјҢдҪҝз”ЁдёҖж¬ЎиҙқеҸ¶ж–ҜеҸҜеҫ—пјҡ
P(Y|X) вҲқ P(Y)*P(X|Y)
В В В з”ЁиҮӘ然иҜӯиЁҖжқҘиҜҙе°ұжҳҜ иҝҷз§ҚеҲҶиҜҚж–№ејҸпјҲиҜҚдёІпјүзҡ„еҸҜиғҪжҖ§ д№ҳд»Ҙ иҝҷдёӘиҜҚдёІз”ҹжҲҗжҲ‘们зҡ„еҸҘеӯҗзҡ„еҸҜиғҪжҖ§гҖӮжҲ‘们иҝӣдёҖжӯҘе®№жҳ“зңӢеҲ°пјҡеҸҜд»Ҙиҝ‘дјјең°е°Ҷ P(X|Y) зңӢдҪңжҳҜжҒ’зӯүдәҺ 1 зҡ„пјҢеӣ дёәд»»ж„ҸеҒҮжғізҡ„дёҖз§ҚеҲҶиҜҚж–№ејҸд№ӢдёӢз”ҹжҲҗжҲ‘们зҡ„еҸҘеӯҗжҖ»жҳҜзІҫеҮҶең°з”ҹжҲҗзҡ„пјҲеҸӘйңҖжҠҠеҲҶиҜҚд№Ӣй—ҙзҡ„еҲҶз•Ңз¬ҰеҸ·жү”жҺүеҚіеҸҜпјүгҖӮдәҺжҳҜпјҢжҲ‘们е°ұеҸҳжҲҗдәҶеҺ»жңҖеӨ§еҢ– P(Y) пјҢд№ҹе°ұжҳҜеҜ»жүҫдёҖз§ҚеҲҶиҜҚдҪҝеҫ—иҝҷдёӘиҜҚдёІпјҲеҸҘеӯҗпјүзҡ„жҰӮзҺҮжңҖеӨ§еҢ–гҖӮиҖҢеҰӮдҪ•и®Ўз®—дёҖдёӘиҜҚдёІпјҡ
W1, W2, W3, W4 ..
В В зҡ„еҸҜиғҪжҖ§е‘ўпјҹжҲ‘们зҹҘйҒ“пјҢж №жҚ®иҒ”еҗҲжҰӮзҺҮзҡ„е…¬ејҸеұ•ејҖпјҡP(W1, W2, W3, W4 ..) = P(W1) * P(W2|W1) * P(W3|W2, W1) * P(W4|W1,W2,W3) * .. дәҺжҳҜжҲ‘们еҸҜд»ҘйҖҡиҝҮдёҖзі»еҲ—зҡ„жқЎд»¶жҰӮзҺҮпјҲеҸіејҸпјүзҡ„д№ҳз§ҜжқҘжұӮж•ҙдёӘиҒ”еҗҲжҰӮзҺҮгҖӮ然иҖҢдёҚе№ёзҡ„жҳҜйҡҸзқҖжқЎд»¶ж•°зӣ®зҡ„еўһеҠ пјҲP(Wn|Wn-1,Wn-2,..,W1) зҡ„жқЎд»¶жңү n-1 дёӘпјүпјҢж•°жҚ®зЁҖз–Ҹй—®йўҳд№ҹдјҡи¶ҠжқҘи¶ҠдёҘйҮҚпјҢеҚідҫҝиҜӯж–ҷеә“еҶҚеӨ§д№ҹж— жі•з»ҹи®ЎеҮәдёҖдёӘйқ и°ұзҡ„ P(Wn|Wn-1,Wn-2,..,W1) жқҘгҖӮдёәдәҶзј“и§ЈиҝҷдёӘй—®йўҳпјҢи®Ўз®—жңә科еӯҰ家们дёҖеҰӮж—ўеҫҖең°дҪҝз”ЁдәҶвҖңеӨ©зңҹвҖқеҒҮи®ҫпјҡжҲ‘们еҒҮи®ҫеҸҘеӯҗдёӯдёҖдёӘиҜҚзҡ„еҮәзҺ°жҰӮзҺҮеҸӘдҫқиө–дәҺе®ғеүҚйқўзҡ„жңүйҷҗзҡ„ k дёӘиҜҚпјҲk дёҖиҲ¬дёҚи¶…иҝҮ 3пјҢеҰӮжһңеҸӘдҫқиө–дәҺеүҚйқўзҡ„дёҖдёӘиҜҚпјҢе°ұжҳҜ2е…ғиҜӯиЁҖжЁЎеһӢпјҲ2-gramпјүпјҢеҗҢзҗҶжңү 3-gram гҖҒ 4-gram зӯүпјүпјҢиҝҷдёӘе°ұжҳҜжүҖи°“зҡ„вҖңжңүйҷҗең°е№ізәҝвҖқеҒҮи®ҫгҖӮ
В В В иҷҪ然дёҠйқўиҝҷдёӘеҒҮи®ҫеҫҲеӮ»еҫҲеӨ©зңҹпјҢдҪҶз»“жһңеҚҙиЎЁжҳҺе®ғзҡ„з»“жһңеҫҖеҫҖжҳҜеҫҲеҘҪеҫҲејәеӨ§зҡ„пјҢеҗҺйқўиҰҒжҸҗеҲ°зҡ„жңҙзҙ иҙқеҸ¶ж–Ҝж–№жі•дҪҝз”Ёзҡ„еҒҮи®ҫи·ҹиҝҷдёӘзІҫзҘһдёҠжҳҜе®Ңе…ЁдёҖиҮҙзҡ„пјҢжҲ‘们дјҡи§ЈйҮҠдёәд»Җд№ҲеғҸиҝҷж ·дёҖдёӘеӨ©зңҹзҡ„еҒҮи®ҫиғҪеӨҹеҫ—еҲ°ејәеӨ§зҡ„з»“жһңгҖӮзӣ®еүҚжҲ‘们еҸӘиҰҒзҹҘйҒ“пјҢжңүдәҶиҝҷдёӘеҒҮи®ҫпјҢеҲҡжүҚйӮЈдёӘд№ҳз§Ҝе°ұеҸҜд»Ҙж”№еҶҷжҲҗпјҡ P(W1) * P(W2|W1) * P(W3|W2) * P(W4|W3) .. пјҲеҒҮи®ҫжҜҸдёӘиҜҚеҸӘдҫқиө–дәҺе®ғеүҚйқўзҡ„дёҖдёӘиҜҚпјүгҖӮиҖҢз»ҹи®Ў P(W2|W1) е°ұдёҚеҶҚеҸ—еҲ°ж•°жҚ®зЁҖз–Ҹй—®йўҳзҡ„еӣ°жү°дәҶгҖӮеҜ№дәҺжҲ‘们дёҠйқўжҸҗеҲ°зҡ„дҫӢеӯҗвҖңеҚ—дә¬еёӮй•ҝжұҹеӨ§жЎҘвҖқпјҢеҰӮжһңжҢүз…§иҮӘе·ҰеҲ°еҸізҡ„иҙӘе©Әж–№жі•еҲҶиҜҚзҡ„иҜқпјҢз»“жһңе°ұжҲҗдәҶвҖңеҚ—дә¬еёӮй•ҝ/жұҹеӨ§жЎҘвҖқгҖӮдҪҶеҰӮжһңжҢүз…§иҙқеҸ¶ж–ҜеҲҶиҜҚзҡ„иҜқпјҲеҒҮи®ҫдҪҝз”Ё 3-gramпјүпјҢз”ұдәҺвҖңеҚ—дә¬еёӮй•ҝвҖқе’ҢвҖңжұҹеӨ§жЎҘвҖқеңЁиҜӯж–ҷеә“дёӯдёҖиө·еҮәзҺ°зҡ„йў‘зҺҮдёә 0 пјҢиҝҷдёӘж•ҙеҸҘзҡ„жҰӮзҺҮдҫҝдјҡиў«еҲӨе®ҡдёә 0 гҖӮ д»ҺиҖҢдҪҝеҫ—вҖңеҚ—дә¬еёӮ/й•ҝжұҹеӨ§жЎҘвҖқиҝҷдёҖеҲҶиҜҚж–№ејҸиғңеҮәгҖӮ
В
2.4.2гҖҒиҙқеҸ¶ж–ҜеӣҫеғҸиҜҶеҲ«пјҢAnalysis by Synthesis
В В иҙқеҸ¶ж–Ҝж–№жі•жҳҜдёҖдёӘйқһеёё general зҡ„жҺЁзҗҶжЎҶжһ¶гҖӮе…¶ж ёеҝғзҗҶеҝөеҸҜд»ҘжҸҸиҝ°жҲҗпјҡAnalysis by Synthesis пјҲйҖҡиҝҮеҗҲжҲҗжқҘеҲҶжһҗпјүгҖӮ06 е№ҙзҡ„и®ӨзҹҘ科еӯҰж–°иҝӣеұ•дёҠжңүдёҖзҜҮ paper е°ұжҳҜи®Із”ЁиҙқеҸ¶ж–ҜжҺЁзҗҶжқҘи§ЈйҮҠи§Ҷи§үиҜҶеҲ«зҡ„пјҢдёҖеӣҫиғңеҚғиЁҖпјҢдёӢеӣҫе°ұжҳҜж‘ҳиҮӘиҝҷзҜҮ paper пјҡ
В
В
В
В
В В йҰ–е…ҲжҳҜи§Ҷи§үзі»з»ҹжҸҗеҸ–еӣҫеҪўзҡ„иҫ№и§’зү№еҫҒпјҢ然еҗҺдҪҝз”Ёиҝҷдәӣзү№еҫҒиҮӘеә•еҗ‘дёҠең°жҝҖжҙ»й«ҳеұӮзҡ„жҠҪиұЎжҰӮеҝөпјҲжҜ”еҰӮжҳҜ E иҝҳжҳҜ F иҝҳжҳҜзӯүеҸ·пјүпјҢ然еҗҺдҪҝз”ЁдёҖдёӘиҮӘйЎ¶еҗ‘дёӢзҡ„йӘҢиҜҒжқҘжҜ”иҫғеҲ°еә•е“ӘдёӘжҰӮеҝөжңҖдҪіең°и§ЈйҮҠдәҶи§ӮеҜҹеҲ°зҡ„еӣҫеғҸгҖӮ
2.4.3гҖҒжңҖеӨ§дјјз„¶дёҺжңҖе°ҸдәҢд№ҳ
В
В
В
В
В В еӯҰиҝҮзәҝжҖ§д»Јж•°зҡ„еӨ§жҰӮйғҪзҹҘйҒ“з»Ҹе…ёзҡ„жңҖе°ҸдәҢд№ҳж–№жі•жқҘеҒҡзәҝжҖ§еӣһеҪ’гҖӮй—®йўҳжҸҸиҝ°жҳҜпјҡз»ҷе®ҡе№ійқўдёҠ N дёӘзӮ№пјҢпјҲиҝҷйҮҢдёҚеҰЁеҒҮи®ҫжҲ‘们жғіз”ЁдёҖжқЎзӣҙзәҝжқҘжӢҹеҗҲиҝҷдәӣзӮ№вҖ”вҖ”еӣһеҪ’еҸҜд»ҘзңӢдҪңжҳҜжӢҹеҗҲзҡ„зү№дҫӢпјҢеҚіе…Ғи®ёиҜҜе·®зҡ„жӢҹеҗҲпјүпјҢжүҫеҮәдёҖжқЎжңҖдҪіжҸҸиҝ°дәҶиҝҷдәӣзӮ№зҡ„зӣҙзәҝгҖӮ
В В дёҖдёӘжҺҘиёөиҖҢжқҘзҡ„й—®йўҳе°ұжҳҜпјҢжҲ‘们еҰӮдҪ•е®ҡд№үжңҖдҪіпјҹжҲ‘们и®ҫжҜҸдёӘзӮ№зҡ„еқҗж Үдёә (Xi, Yi) гҖӮеҰӮжһңзӣҙзәҝдёә y = f(x) гҖӮйӮЈд№Ҳ (Xi, Yi) и·ҹзӣҙзәҝеҜ№иҝҷдёӘзӮ№зҡ„вҖңйў„жөӢвҖқпјҡ(Xi, f(Xi)) е°ұзӣёе·®дәҶдёҖдёӘ О”Yi = |Yi вҖ“ f(Xi)| гҖӮжңҖе°ҸдәҢд№ҳе°ұжҳҜиҜҙеҜ»жүҫзӣҙзәҝдҪҝеҫ— (О”Y1)^2 + (О”Y2)^2 + .. пјҲеҚіиҜҜе·®зҡ„е№іж–№е’ҢпјүжңҖе°ҸпјҢиҮідәҺдёәд»Җд№ҲжҳҜиҜҜе·®зҡ„е№іж–№е’ҢиҖҢдёҚжҳҜиҜҜе·®зҡ„з»қеҜ№еҖје’ҢпјҢз»ҹи®ЎеӯҰдёҠд№ҹжІЎжңүд»Җд№ҲеҘҪзҡ„и§ЈйҮҠгҖӮ然иҖҢиҙқеҸ¶ж–Ҝж–№жі•еҚҙиғҪеҜ№жӯӨжҸҗдҫӣдёҖдёӘе®ҢзҫҺзҡ„и§ЈйҮҠгҖӮ
В В жҲ‘们еҒҮи®ҫзӣҙзәҝеҜ№дәҺеқҗж Ү Xi з»ҷеҮәзҡ„йў„жөӢ f(Xi) жҳҜжңҖйқ и°ұзҡ„йў„жөӢпјҢжүҖжңүзәөеқҗж ҮеҒҸзҰ» f(Xi) зҡ„йӮЈдәӣж•°жҚ®зӮ№йғҪеҗ«жңүеҷӘйҹіпјҢжҳҜеҷӘйҹідҪҝеҫ—е®ғ们еҒҸзҰ»дәҶе®ҢзҫҺзҡ„дёҖжқЎзӣҙзәҝпјҢдёҖдёӘеҗҲзҗҶзҡ„еҒҮи®ҫе°ұжҳҜеҒҸзҰ»и·Ҝзәҝи¶Ҡиҝңзҡ„жҰӮзҺҮи¶Ҡе°ҸпјҢе…·дҪ“е°ҸеӨҡе°‘пјҢеҸҜд»Ҙз”ЁдёҖдёӘжӯЈжҖҒеҲҶеёғжӣІзәҝжқҘжЁЎжӢҹпјҢиҝҷдёӘеҲҶеёғжӣІзәҝд»ҘзӣҙзәҝеҜ№ Xi з»ҷеҮәзҡ„йў„жөӢ f(Xi) дёәдёӯеҝғпјҢе®һйҷ…зәөеқҗж Үдёә Yi зҡ„зӮ№ (Xi, Yi) еҸ‘з”ҹзҡ„жҰӮзҺҮе°ұжӯЈжҜ”дәҺ EXP[-(О”Yi)^2]гҖӮпјҲEXP(..) д»ЈиЎЁд»Ҙеёёж•° e дёәеә•зҡ„еӨҡе°‘ж¬Ўж–№пјүгҖӮ
В В зҺ°еңЁжҲ‘们еӣһеҲ°й—®йўҳзҡ„иҙқеҸ¶ж–Ҝж–№йқўпјҢжҲ‘们иҰҒжғіжңҖеӨ§еҢ–зҡ„еҗҺйӘҢжҰӮзҺҮжҳҜпјҡ
P(h|D) вҲқ P(h) * P(D|h)
В
В В еҸҲи§ҒиҙқеҸ¶ж–ҜпјҒиҝҷйҮҢ h е°ұжҳҜжҢҮдёҖжқЎзү№е®ҡзҡ„зӣҙзәҝпјҢD е°ұжҳҜжҢҮиҝҷ N дёӘж•°жҚ®зӮ№гҖӮжҲ‘们йңҖиҰҒеҜ»жүҫдёҖжқЎзӣҙзәҝ h дҪҝеҫ— P(h) * P(D|h) жңҖеӨ§гҖӮеҫҲжҳҫ然пјҢP(h) иҝҷдёӘе…ҲйӘҢжҰӮзҺҮжҳҜеқҮеҢҖзҡ„пјҢеӣ дёәе“ӘжқЎзӣҙзәҝд№ҹдёҚжҜ”еҸҰдёҖжқЎжӣҙдјҳи¶ҠгҖӮжүҖд»ҘжҲ‘们еҸӘйңҖиҰҒзңӢ P(D|h) иҝҷдёҖйЎ№пјҢиҝҷдёҖйЎ№жҳҜжҢҮиҝҷжқЎзӣҙзәҝз”ҹжҲҗиҝҷдәӣж•°жҚ®зӮ№зҡ„жҰӮзҺҮпјҢеҲҡжүҚиҜҙиҝҮдәҶпјҢз”ҹжҲҗж•°жҚ®зӮ№ (Xi, Yi) зҡ„жҰӮзҺҮдёә EXP[-(О”Yi)^2] д№ҳд»ҘдёҖдёӘеёёж•°гҖӮиҖҢ P(D|h) = P(d1|h) * P(d2|h) * .. еҚіеҒҮи®ҫеҗ„дёӘж•°жҚ®зӮ№жҳҜзӢ¬з«Ӣз”ҹжҲҗзҡ„пјҢжүҖд»ҘеҸҜд»ҘжҠҠжҜҸдёӘжҰӮзҺҮд№ҳиө·жқҘгҖӮдәҺжҳҜз”ҹжҲҗ N дёӘж•°жҚ®зӮ№зҡ„жҰӮзҺҮдёә EXP[-(О”Y1)^2] * EXP[-(О”Y2)^2] * EXP[-(О”Y3)^2] * .. = EXP{-[(О”Y1)^2 + (О”Y2)^2 + (О”Y3)^2 + ..]} жңҖеӨ§еҢ–иҝҷдёӘжҰӮзҺҮе°ұжҳҜиҰҒжңҖе°ҸеҢ– (О”Y1)^2 + (О”Y2)^2 + (О”Y3)^2 + .. гҖӮ зҶҹжӮүиҝҷдёӘејҸеӯҗеҗ—пјҹ
В В йҷӨдәҶд»ҘдёҠжүҖд»Ӣз»Қзҡ„д№ӢеӨ–пјҢиҙқеҸ¶ж–ҜиҝҳеңЁиҜҚд№үж¶ҲеІҗпјҢиҜӯиЁҖжЁЎеһӢзҡ„е№іж»‘ж–№жі•дёӯйғҪжңүдёҖе®ҡеә”з”ЁгҖӮдёӢиҠӮпјҢе’ұ们еҶҚжқҘз®ҖеҚ•зңӢдёӢжңҙзҙ иҙқеҸ¶ж–Ҝж–№жі•гҖӮ
2.5гҖҒжңҙзҙ иҙқеҸ¶ж–Ҝж–№жі•
В В жңҙзҙ иҙқеҸ¶ж–Ҝж–№жі•жҳҜдёҖдёӘеҫҲзү№еҲ«зҡ„ж–№жі•пјҢжүҖд»ҘеҖјеҫ—д»Ӣз»ҚдёҖдёӢгҖӮеңЁдј—еӨҡзҡ„еҲҶзұ»жЁЎеһӢдёӯпјҢеә”з”ЁжңҖдёәе№ҝжіӣзҡ„дёӨз§ҚеҲҶзұ»жЁЎеһӢжҳҜеҶізӯ–ж ‘жЁЎеһӢ(Decision Tree Model)е’Ңжңҙзҙ иҙқеҸ¶ж–ҜжЁЎеһӢпјҲNaive Bayesian ModelпјҢNBCпјүгҖӮВ жңҙзҙ иҙқеҸ¶ж–ҜжЁЎеһӢеҸ‘жәҗдәҺеҸӨе…ёж•°еӯҰзҗҶи®әпјҢжңүзқҖеқҡе®һзҡ„ж•°еӯҰеҹәзЎҖпјҢд»ҘеҸҠзЁіе®ҡзҡ„еҲҶзұ»ж•ҲзҺҮгҖӮ
В В В еҗҢж—¶пјҢNBCжЁЎеһӢжүҖйңҖдј°и®Ўзҡ„еҸӮж•°еҫҲе°‘пјҢеҜ№зјәеӨұж•°жҚ®дёҚеӨӘж•Ҹж„ҹпјҢз®—жі•д№ҹжҜ”иҫғз®ҖеҚ•гҖӮзҗҶи®әдёҠпјҢNBCжЁЎеһӢдёҺе…¶д»–еҲҶзұ»ж–№жі•зӣёжҜ”е…·жңүжңҖе°Ҹзҡ„иҜҜе·®зҺҮгҖӮдҪҶжҳҜе®һйҷ…дёҠ并йқһжҖ»жҳҜеҰӮжӯӨпјҢиҝҷжҳҜеӣ дёәNBCжЁЎеһӢеҒҮи®ҫеұһжҖ§д№Ӣй—ҙзӣёдә’зӢ¬з«ӢпјҢиҝҷдёӘеҒҮи®ҫеңЁе®һйҷ…еә”з”ЁдёӯеҫҖеҫҖжҳҜдёҚжҲҗз«Ӣзҡ„пјҢиҝҷз»ҷNBCжЁЎеһӢзҡ„жӯЈзЎ®еҲҶзұ»еёҰжқҘдәҶдёҖе®ҡеҪұе“ҚгҖӮеңЁеұһжҖ§дёӘж•°жҜ”иҫғеӨҡжҲ–иҖ…еұһжҖ§д№Ӣй—ҙзӣёе…іжҖ§иҫғеӨ§ж—¶пјҢNBCжЁЎеһӢзҡ„еҲҶзұ»ж•ҲзҺҮжҜ”дёҚдёҠеҶізӯ–ж ‘жЁЎеһӢгҖӮиҖҢеңЁеұһжҖ§зӣёе…іжҖ§иҫғе°Ҹж—¶пјҢNBCжЁЎеһӢзҡ„жҖ§иғҪжңҖдёәиүҜеҘҪгҖӮ
В В жҺҘдёӢжқҘпјҢжҲ‘们用жңҙзҙ иҙқеҸ¶ж–ҜеңЁеһғеңҫйӮ®д»¶иҝҮж»Өдёӯзҡ„еә”з”ЁжқҘдёҫдҫӢиҜҙжҳҺгҖӮ
2.5.1гҖҒиҙқеҸ¶ж–ҜеһғеңҫйӮ®д»¶иҝҮж»ӨеҷЁ
В В й—®йўҳжҳҜд»Җд№Ҳпјҹй—®йўҳжҳҜпјҢз»ҷе®ҡдёҖе°ҒйӮ®д»¶пјҢеҲӨе®ҡе®ғжҳҜеҗҰеұһдәҺеһғеңҫйӮ®д»¶гҖӮжҢүз…§е…ҲдҫӢпјҢжҲ‘们иҝҳжҳҜз”Ё D жқҘиЎЁзӨәиҝҷе°ҒйӮ®д»¶пјҢжіЁж„Ҹ D з”ұ N дёӘеҚ•иҜҚз»„жҲҗгҖӮжҲ‘们用 h+ жқҘиЎЁзӨәеһғеңҫйӮ®д»¶пјҢh- иЎЁзӨәжӯЈеёёйӮ®д»¶гҖӮй—®йўҳеҸҜд»ҘеҪўејҸеҢ–ең°жҸҸиҝ°дёәжұӮпјҡ
P(h+|D) = P(h+) * P(D|h+) / P(D)
В
P(h-|D) = P(h-) * P(D|h-) / P(D)
В
В В е…¶дёӯ P(h+) е’Ң P(h-) иҝҷдёӨдёӘе…ҲйӘҢжҰӮзҺҮйғҪжҳҜеҫҲе®№жҳ“жұӮеҮәжқҘзҡ„пјҢеҸӘйңҖиҰҒи®Ўз®—дёҖдёӘйӮ®д»¶еә“йҮҢйқўеһғеңҫйӮ®д»¶е’ҢжӯЈеёёйӮ®д»¶зҡ„жҜ”дҫӢе°ұиЎҢдәҶгҖӮ然иҖҢ P(D|h+) еҚҙдёҚе®№жҳ“жұӮпјҢеӣ дёә D йҮҢйқўеҗ«жңү N дёӘеҚ•иҜҚ d1, d2, d3, .. пјҢжүҖд»ҘP(D|h+) = P(d1,d2,..,dn|h+) гҖӮжҲ‘们еҸҲдёҖж¬ЎйҒҮеҲ°дәҶж•°жҚ®зЁҖз–ҸжҖ§пјҢдёәд»Җд№Ҳиҝҷд№ҲиҜҙе‘ўпјҹP(d1,d2,..,dn|h+) е°ұжҳҜиҜҙеңЁеһғеңҫйӮ®д»¶еҪ“дёӯеҮәзҺ°и·ҹжҲ‘们зӣ®еүҚиҝҷе°ҒйӮ®д»¶дёҖжЁЎдёҖж ·зҡ„дёҖе°ҒйӮ®д»¶зҡ„жҰӮзҺҮжҳҜеӨҡеӨ§пјҒејҖзҺ©з¬‘пјҢжҜҸе°ҒйӮ®д»¶йғҪжҳҜдёҚеҗҢзҡ„пјҢдё–з•ҢдёҠжңүж— з©·еӨҡе°ҒйӮ®д»¶гҖӮзһ§пјҢиҝҷе°ұжҳҜж•°жҚ®зЁҖз–ҸжҖ§пјҢеӣ дёәеҸҜд»ҘиӮҜе®ҡең°иҜҙпјҢдҪ 收йӣҶзҡ„и®ӯз»ғж•°жҚ®еә“дёҚз®ЎйҮҢйқўеҗ«дәҶеӨҡе°‘е°ҒйӮ®д»¶пјҢд№ҹдёҚеҸҜиғҪжүҫеҮәдёҖе°Ғи·ҹзӣ®еүҚиҝҷе°ҒдёҖжЁЎдёҖж ·зҡ„гҖӮз»“жһңе‘ўпјҹжҲ‘们еҸҲиҜҘеҰӮдҪ•жқҘи®Ўз®— P(d1,d2,..,dn|h+) е‘ўпјҹ
В В жҲ‘们е°Ҷ P(d1,d2,..,dn|h+)В жү©еұ•дёәпјҡ P(d1|h+) * P(d2|d1, h+) * P(d3|d2,d1, h+) * .. гҖӮзҶҹжӮүиҝҷдёӘејҸеӯҗеҗ—пјҹиҝҷйҮҢжҲ‘们дјҡдҪҝз”ЁдёҖдёӘжӣҙжҝҖиҝӣзҡ„еҒҮи®ҫпјҢжҲ‘们еҒҮи®ҫ di дёҺ di-1 жҳҜе®Ңе…ЁжқЎд»¶ж— е…ізҡ„пјҢдәҺжҳҜејҸеӯҗе°ұз®ҖеҢ–дёә P(d1|h+) * P(d2|h+) * P(d3|h+) * .. гҖӮиҝҷдёӘе°ұжҳҜжүҖи°“зҡ„жқЎд»¶зӢ¬з«ӢеҒҮи®ҫпјҢд№ҹжӯЈжҳҜжңҙзҙ иҙқеҸ¶ж–Ҝж–№жі•зҡ„жңҙзҙ д№ӢеӨ„гҖӮиҖҢи®Ўз®— P(d1|h+) * P(d2|h+) * P(d3|h+) * .. е°ұеӨӘз®ҖеҚ•дәҶпјҢеҸӘиҰҒз»ҹи®Ў di иҝҷдёӘеҚ•иҜҚеңЁеһғеңҫйӮ®д»¶дёӯеҮәзҺ°зҡ„йў‘зҺҮеҚіеҸҜгҖӮе…ідәҺиҙқеҸ¶ж–ҜеһғеңҫйӮ®д»¶иҝҮж»ӨжӣҙеӨҡзҡ„еҶ…е®№еҸҜд»ҘеҸӮиҖғиҝҷдёӘжқЎзӣ®пјҢжіЁж„Ҹе…¶дёӯжҸҗеҲ°зҡ„е…¶д»–иө„ж–ҷгҖӮ
2.6гҖҒеұӮзә§иҙқеҸ¶ж–ҜжЁЎеһӢ
В
В
В
В
В В В еұӮзә§иҙқеҸ¶ж–ҜжЁЎеһӢжҳҜзҺ°д»ЈиҙқеҸ¶ж–Ҝж–№жі•зҡ„ж Үеҝ—жҖ§е»әзӯ‘д№ӢдёҖгҖӮеүҚйқўи®Ізҡ„иҙқеҸ¶ж–ҜпјҢйғҪжҳҜеңЁеҗҢдёҖдёӘдәӢзү©еұӮж¬ЎдёҠзҡ„еҗ„дёӘеӣ зҙ д№Ӣй—ҙиҝӣиЎҢз»ҹи®ЎжҺЁзҗҶпјҢ然иҖҢеұӮж¬ЎиҙқеҸ¶ж–ҜжЁЎеһӢеңЁе“ІеӯҰдёҠжӣҙж·ұе…ҘдәҶдёҖеұӮпјҢе°Ҷиҝҷдәӣеӣ зҙ иғҢеҗҺзҡ„еӣ зҙ пјҲеҺҹеӣ зҡ„еҺҹеӣ пјҢеҺҹеӣ зҡ„еҺҹеӣ пјҢд»ҘжӯӨзұ»жҺЁпјүеӣҠжӢ¬иҝӣжқҘгҖӮдёҖдёӘж•ҷ科д№ҰдҫӢеӯҗжҳҜпјҡеҰӮжһңдҪ жүӢеӨҙжңү N жһҡзЎ¬еёҒпјҢе®ғ们жҳҜеҗҢдёҖдёӘе·ҘеҺӮй“ёеҮәжқҘзҡ„пјҢдҪ жҠҠжҜҸдёҖжһҡзЎ¬еёҒжҺ·еҮәдёҖдёӘз»“жһңпјҢ然еҗҺеҹәдәҺиҝҷ N дёӘз»“жһңеҜ№иҝҷ N дёӘзЎ¬еёҒзҡ„ Оё пјҲеҮәзҺ°жӯЈйқўзҡ„жҜ”дҫӢпјүиҝӣиЎҢжҺЁзҗҶгҖӮеҰӮжһңж №жҚ®жңҖеӨ§дјјз„¶пјҢжҜҸдёӘзЎ¬еёҒзҡ„ Оё дёҚжҳҜ 1 е°ұжҳҜ 0 пјҲиҝҷдёӘеүҚйқўжҸҗеҲ°иҝҮзҡ„пјүпјҢ然иҖҢжҲ‘们еҸҲзҹҘйҒ“жҜҸдёӘзЎ¬еёҒзҡ„ p(Оё) жҳҜжңүдёҖдёӘе…ҲйӘҢжҰӮзҺҮзҡ„пјҢд№ҹи®ёжҳҜдёҖдёӘ beta еҲҶеёғгҖӮд№ҹе°ұжҳҜиҜҙпјҢжҜҸдёӘзЎ¬еёҒзҡ„е®һйҷ…жҠ•жҺ·з»“жһң Xi жңҚд»Һд»Ҙ Оё дёәдёӯеҝғзҡ„жӯЈжҖҒеҲҶеёғпјҢиҖҢ Оё еҸҲжңҚд»ҺеҸҰдёҖдёӘд»Ҙ ОЁ дёәдёӯеҝғзҡ„ beta еҲҶеёғгҖӮеұӮеұӮеӣ жһңе…ізі»е°ұдҪ“зҺ°еҮәжқҘдәҶгҖӮиҝӣиҖҢ ОЁ иҝҳеҸҜиғҪдҫқиө–дәҺеӣ жһңй“ҫдёҠжӣҙдёҠеұӮзҡ„еӣ зҙ пјҢд»ҘжӯӨзұ»жҺЁгҖӮ
2.7гҖҒеҹәдәҺnewsgroupж–ҮжЎЈйӣҶзҡ„иҙқеҸ¶ж–Ҝз®—жі•е®һзҺ°
2.7.1гҖҒnewsgroupж–ҮжЎЈйӣҶд»Ӣз»ҚдёҺйў„еӨ„зҗҶ
В В NewsgroupsжңҖж—©з”ұLangдәҺ1995收йӣҶ并еңЁ[Lang 1995]дёӯдҪҝз”ЁгҖӮе®ғеҗ«жңү20000зҜҮе·ҰеҸізҡ„Usenetж–ҮжЎЈпјҢеҮ д№Һе№іеқҮеҲҶй…Қ20дёӘдёҚеҗҢзҡ„ж–°й—»з»„гҖӮйҷӨдәҶе…¶дёӯ4.5%зҡ„ж–ҮжЎЈеұһдәҺдёӨдёӘжҲ–дёӨдёӘд»ҘдёҠзҡ„ж–°й—»з»„д»ҘеӨ–пјҢе…¶дҪҷж–ҮжЎЈд»…еұһдәҺдёҖдёӘж–°й—»з»„пјҢеӣ жӯӨе®ғйҖҡеёёиў«дҪңдёәеҚ•ж ҮжіЁеҲҶзұ»й—®йўҳжқҘеӨ„зҗҶгҖӮNewsgroupsе·Із»ҸжҲҗдёәж–Үжң¬еҲҶзұ»иҒҡзұ»дёӯеёёз”Ёзҡ„ж–ҮжЎЈйӣҶгҖӮзҫҺеӣҪMITеӨ§еӯҰJason RennieеҜ№NewsgroupsдҪңдәҶеҝ…иҰҒзҡ„еӨ„зҗҶпјҢдҪҝеҫ—жҜҸдёӘж–ҮжЎЈеҸӘеұһдәҺдёҖдёӘж–°й—»з»„пјҢеҪўжҲҗNewsgroups-18828гҖӮВ
В
В пјҲжіЁпјҡжң¬2.7иҠӮеҶ…е®№дё»иҰҒжҸҙеј•иҮӘеҸӮиҖғж–ҮзҢ®жқЎзӣ®8зҡ„еҶ…е®№пјҢжңүд»»дҪ•дёҚеҰҘд№ӢеӨ„пјҢиҝҳжңӣеҺҹдҪңиҖ…еҸҠдј—иҜ»иҖ…жө·ж¶өпјҢи°ўи°ў)
В
В В иҰҒеҒҡж–Үжң¬еҲҶзұ»йҰ–е…Ҳеҫ—е®ҢжҲҗж–Үжң¬зҡ„йў„еӨ„зҗҶпјҢйў„еӨ„зҗҶзҡ„дё»иҰҒжӯҘйӘӨеҰӮдёӢпјҡ
- иӢұж–ҮиҜҚжі•еҲҶжһҗпјҢеҺ»йҷӨж•°еӯ—гҖҒиҝһеӯ—з¬ҰгҖҒж ҮзӮ№з¬ҰеҸ·гҖҒзү№ж®ҠВ еӯ—з¬ҰпјҢжүҖжңүеӨ§еҶҷеӯ—жҜҚиҪ¬жҚўжҲҗе°ҸеҶҷпјҢеҸҜд»Ҙз”ЁжӯЈеҲҷиЎЁиҫҫејҸпјҡString res[] = line.split("[^a-zA-Z]")пјӣ
- еҺ»еҒңз”ЁиҜҚпјҢиҝҮж»ӨеҜ№еҲҶзұ»ж— д»·еҖјзҡ„иҜҚпјӣ
- иҜҚж №иҝҳеҺҹstemmingпјҢеҹәдәҺPorterз®—жі•гҖӮ
- privateВ staticВ StringВ lineProcess(StringВ line,В ArrayList<String>В stopWordsArray)В throwsВ IOExceptionВ {В В В В
- В В В В //В TODOВ Auto-generatedВ methodВ stubВ В В В
- В В В В //step1В иӢұж–ҮиҜҚжі•еҲҶжһҗпјҢеҺ»йҷӨж•°еӯ—гҖҒиҝһеӯ—з¬ҰгҖҒж ҮзӮ№з¬ҰеҸ·гҖҒзү№ж®Ҡеӯ—з¬ҰпјҢжүҖжңүеӨ§еҶҷеӯ—жҜҚиҪ¬жҚўжҲҗе°ҸеҶҷпјҢеҸҜд»ҘиҖғиҷ‘з”ЁжӯЈеҲҷиЎЁиҫҫејҸВ В В В
- В В В В StringВ res[]В =В line.split("[^a-zA-Z]");В В В В
- В В В В //иҝҷйҮҢиҰҒе°ҸеҝғпјҢйҳІжӯўжҠҠжңүеҚ•иҜҚдёӯй—ҙжңүж•°еӯ—е’Ңиҝһеӯ—з¬Ұзҡ„еҚ•иҜҚВ жҲӘж–ӯдәҶпјҢдҪҶжҳҜжҲӘж–ӯд№ҹжІЎдәӢВ В В В
- В В В В В В В В
- В В В В StringВ resStringВ =В newВ String();В В В В
- В В В В //step2еҺ»еҒңз”ЁиҜҚВ В В В
- В В В В //step3stemming,иҝ”еӣһеҗҺдёҖиө·еҒҡВ В В В
- В В В В for(intВ iВ =В 0;В iВ <В res.length;В i++){В В В В
- В В В В В В В В if(!res[i].isEmpty()В &&В !stopWordsArray.contains(res[i].toLowerCase())){В В В В
- В В В В В В В В В В В В resStringВ +=В "В "В +В res[i].toLowerCase()В +В "В ";В В В В
- В В В В В В В В }В В В В
- В В В В }В В В В
- В В В В returnВ resString;В В В В
- }В В В
2.7.2гҖҒзү№еҫҒиҜҚзҡ„йҖүеҸ–
еҮәзҺ°ж¬Ўж•°еӨ§дәҺзӯүдәҺ1ж¬Ўзҡ„иҜҚжңү87554дёӘ
еҮәзҺ°ж¬Ўж•°еӨ§дәҺзӯүдәҺ3ж¬Ўзҡ„иҜҚжңү36456дёӘВ
еҮәзҺ°ж¬Ўж•°еӨ§дәҺзӯүдәҺ4ж¬Ўзҡ„иҜҚжңү30095дёӘ
В В зү№еҫҒиҜҚзҡ„йҖүеҸ–зӯ–з•Ҙпјҡ
зӯ–з•ҘдёҖпјҡдҝқз•ҷжүҖжңүиҜҚдҪңдёәзү№еҫҒиҜҚ е…ұи®Ў87554дёӘ
зӯ–з•ҘдәҢпјҡйҖүеҸ–еҮәзҺ°ж¬Ўж•°еӨ§дәҺзӯүдәҺ4ж¬Ўзҡ„иҜҚдҪңдёәзү№еҫҒиҜҚе…ұи®Ў30095дёӘВ
В В зү№еҫҒиҜҚзҡ„йҖүеҸ–зӯ–з•ҘпјҡйҮҮз”Ёзӯ–з•ҘдёҖпјҢеҗҺйқўе°ҶеҜ№дёӨз§Қзү№еҫҒиҜҚйҖүеҸ–зӯ–з•Ҙзҡ„и®Ўз®—ж—¶й—ҙе’Ңе№іеқҮеҮҶзЎ®зҺҮеҒҡеҜ№жҜ”
2.7.3гҖҒиҙқеҸ¶ж–Ҝз®—жі•жҸҸиҝ°еҸҠе®һзҺ°
В
зұ»жқЎд»¶жҰӮзҺҮP(tk|c)=(зұ»cдёӢеҚ•иҜҚtkеңЁеҗ„дёӘж–ҮжЎЈдёӯеҮәзҺ°иҝҮзҡ„ж¬Ўж•°д№Ӣе’Ң+1)/пјҲзұ»cдёӢеҚ•иҜҚжҖ»ж•°+и®ӯз»ғж ·жң¬дёӯдёҚйҮҚеӨҚзү№еҫҒиҜҚжҖ»ж•°пјү
е…ҲйӘҢжҰӮзҺҮP(c)=зұ»cдёӢзҡ„еҚ•иҜҚжҖ»ж•°/ж•ҙдёӘи®ӯз»ғж ·жң¬зҡ„еҚ•иҜҚжҖ»ж•°
жң¬еҲҶзұ»еҷЁйҖүз”ЁеӨҡйЎ№ејҸжЁЎеһӢи®Ўз®—пјҢж №жҚ®ж–ҜеқҰзҰҸзҡ„гҖҠIntroduction to Information Retrieval гҖӢиҜҫ件дёҠжүҖиҜҙпјҢеӨҡйЎ№ејҸжЁЎеһӢи®Ўз®—еҮҶзЎ®зҺҮжӣҙй«ҳгҖӮ
- и®Ўз®—жҰӮзҺҮз”ЁеҲ°дәҶBigDecimalзұ»е®һзҺ°д»»ж„ҸзІҫеәҰи®Ўз®—пјӣ
- з”ЁдәӨеҸүйӘҢиҜҒжі•еҒҡеҚҒж¬ЎеҲҶзұ»е®һйӘҢпјҢеҜ№еҮҶзЎ®зҺҮеҸ–е№іеқҮеҖјпјӣ
- ж №жҚ®жӯЈзЎ®зұ»зӣ®ж–Ү件е’ҢеҲҶзұ»з»“жһңж–Үи®Ўз®—ж··ж·Ҷзҹ©йҳө并且иҫ“еҮәпјӣ
- В Map<String,Double> cateWordsProb keyдёәвҖңзұ»зӣ®_еҚ•иҜҚвҖқ, valueдёәиҜҘзұ»зӣ®дёӢиҜҘеҚ•иҜҚзҡ„еҮәзҺ°ж¬Ўж•°пјҢйҒҝе…ҚйҮҚеӨҚи®Ўз®—гҖӮ
В
- packageВ com.pku.yangliu;В В
- importВ java.io.BufferedReader;В В
- importВ java.io.File;В В
- importВ java.io.FileReader;В В
- importВ java.io.FileWriter;В В
- importВ java.io.IOException;В В
- importВ java.math.BigDecimal;В В
- importВ java.util.Iterator;В В
- importВ java.util.Map;В В
- importВ java.util.Set;В В
- importВ java.util.SortedSet;В В
- importВ java.util.TreeMap;В В
- importВ java.util.TreeSet;В В
- importВ java.util.Vector;В В
- В В
- /**еҲ©з”Ёжңҙзҙ иҙқеҸ¶ж–Ҝз®—жі•еҜ№newsgroupж–ҮжЎЈйӣҶеҒҡеҲҶзұ»пјҢйҮҮз”ЁеҚҒз»„дәӨеҸүжөӢиҜ•еҸ–е№іеқҮеҖјВ
- В *В йҮҮз”ЁеӨҡйЎ№ејҸжЁЎеһӢ,stanfordдҝЎжҒҜжЈҖзҙўеҜји®әиҜҫ件дёҠйқўиЁҖеӨҡйЎ№ејҸжЁЎеһӢжҜ”дјҜеҠӘеҲ©жЁЎеһӢеҮҶзЎ®еәҰй«ҳВ
- В *В зұ»жқЎд»¶жҰӮзҺҮP(tk|c)=(зұ»cВ дёӢеҚ•иҜҚtkВ еңЁеҗ„дёӘж–ҮжЎЈдёӯеҮәзҺ°иҝҮзҡ„ж¬Ўж•°д№Ӣе’Ң+1)/(зұ»cдёӢеҚ•иҜҚжҖ»ж•°+|V|)В
- В */В В
- publicВ classВ NaiveBayesianClassifierВ {В В
- В В В В В В
- В В В В /**з”ЁиҙқеҸ¶ж–Ҝжі•еҜ№жөӢиҜ•ж–ҮжЎЈйӣҶеҲҶзұ»В
- В В В В В *В @paramВ trainDirВ и®ӯз»ғж–ҮжЎЈйӣҶзӣ®еҪ•В
- В В В В В *В @paramВ testDirВ жөӢиҜ•ж–ҮжЎЈйӣҶзӣ®еҪ•В
- В В В В В *В @paramВ classifyResultFileNewВ еҲҶзұ»з»“жһңж–Ү件и·Ҝеҫ„В
- В В В В В *В @throwsВ ExceptionВ В
- В В В В В */В В
- В В В В privateВ voidВ doProcess(StringВ trainDir,В StringВ testDir,В В
- В В В В В В В В В В В В StringВ classifyResultFileNew)В throwsВ ExceptionВ {В В
- В В В В В В В В //В TODOВ Auto-generatedВ methodВ stubВ В
- В В В В В В В В Map<String,Double>В cateWordsNumВ =В newВ TreeMap<String,Double>();//дҝқеӯҳи®ӯз»ғйӣҶжҜҸдёӘзұ»еҲ«зҡ„жҖ»иҜҚж•°В В
- В В В В В В В В Map<String,Double>В cateWordsProbВ =В newВ TreeMap<String,Double>();//дҝқеӯҳи®ӯз»ғж ·жң¬жҜҸдёӘзұ»еҲ«дёӯжҜҸдёӘеұһжҖ§иҜҚзҡ„еҮәзҺ°иҜҚж•°В В
- В В В В В В В В cateWordsProbВ =В getCateWordsProb(trainDir);В В
- В В В В В В В В cateWordsNumВ =В getCateWordsNum(trainDir);В В
- В В В В В В В В doubleВ totalWordsNumВ =В 0.0;//и®°еҪ•жүҖжңүи®ӯз»ғйӣҶзҡ„жҖ»иҜҚж•°В В
- В В В В В В В В Set<Map.Entry<String,Double>>В cateWordsNumSetВ =В cateWordsNum.entrySet();В В
- В В В В В В В В for(Iterator<Map.Entry<String,Double>>В itВ =В cateWordsNumSet.iterator();В it.hasNext();){В В
- В В В В В В В В В В В В Map.Entry<String,В Double>В meВ =В it.next();В В
- В В В В В В В В В В В В totalWordsNumВ +=В me.getValue();В В
- В В В В В В В В }В В
- В В В В В В В В //дёӢйқўејҖе§ӢиҜ»еҸ–жөӢиҜ•ж ·дҫӢеҒҡеҲҶзұ»В В
- В В В В В В В В Vector<String>В testFileWordsВ =В newВ Vector<String>();В В
- В В В В В В В В StringВ word;В В
- В В В В В В В В File[]В testDirFilesВ =В newВ File(testDir).listFiles();В В
- В В В В В В В В FileWriterВ crWriterВ =В newВ FileWriter(classifyResultFileNew);В В
- В В В В В В В В for(intВ iВ =В 0;В iВ <В testDirFiles.length;В i++){В В
- В В В В В В В В В В В В File[]В testSampleВ =В testDirFiles[i].listFiles();В В
- В В В В В В В В В В В В for(intВ jВ =В 0;jВ <В testSample.length;В j++){В В
- В В В В В В В В В В В В В В В В testFileWords.clear();В В
- В В В В В В В В В В В В В В В В FileReaderВ spReaderВ =В newВ FileReader(testSample[j]);В В
- В В В В В В В В В В В В В В В В BufferedReaderВ spBRВ =В newВ BufferedReader(spReader);В В
- В В В В В В В В В В В В В В В В while((wordВ =В spBR.readLine())В !=В null){В В
- В В В В В В В В В В В В В В В В В В В В testFileWords.add(word);В В
- В В В В В В В В В В В В В В В В }В В
- В В В В В В В В В В В В В В В В //дёӢйқўеҲҶеҲ«и®Ўз®—иҜҘжөӢиҜ•ж ·дҫӢеұһдәҺдәҢеҚҒдёӘзұ»еҲ«зҡ„жҰӮзҺҮВ В
- В В В В В В В В В В В В В В В В File[]В trainDirFilesВ =В newВ File(trainDir).listFiles();В В
- В В В В В В В В В В В В В В В В BigDecimalВ maxPВ =В newВ BigDecimal(0);В В
- В В В В В В В В В В В В В В В В StringВ bestCateВ =В null;В В
- В В В В В В В В В В В В В В В В for(intВ kВ =В 0;В kВ <В trainDirFiles.length;В k++){В В
- В В В В В В В В В В В В В В В В В В В В BigDecimalВ pВ =В computeCateProb(trainDirFiles[k],В testFileWords,В cateWordsNum,В totalWordsNum,В cateWordsProb);В В
- В В В В В В В В В В В В В В В В В В В В if(kВ ==В 0){В В
- В В В В В В В В В В В В В В В В В В В В В В В В maxPВ =В p;В В
- В В В В В В В В В В В В В В В В В В В В В В В В bestCateВ =В trainDirFiles[k].getName();В В
- В В В В В В В В В В В В В В В В В В В В В В В В continue;В В
- В В В В В В В В В В В В В В В В В В В В }В В
- В В В В В В В В В В В В В В В В В В В В if(p.compareTo(maxP)В ==В 1){В В
- В В В В В В В В В В В В В В В В В В В В В В В В maxPВ =В p;В В
- В В В В В В В В В В В В В В В В В В В В В В В В bestCateВ =В trainDirFiles[k].getName();В В
- В В В В В В В В В В В В В В В В В В В В }В В
- В В В В В В В В В В В В В В В В }В В
- В В В В В В В В В В В В В В В В crWriter.append(testSample[j].getName()В +В "В "В +В bestCateВ +В "\n");В В
- В В В В В В В В В В В В В В В В crWriter.flush();В В
- В В В В В В В В В В В В }В В
- В В В В В В В В }В В
- В В В В В В В В crWriter.close();В В
- В В В В }В В
- В В В В В В
- В В В В /**з»ҹи®Ўжҹҗзұ»и®ӯз»ғж ·жң¬дёӯжҜҸдёӘеҚ•иҜҚзҡ„еҮәзҺ°ж¬Ўж•°В
- В В В В В *В @paramВ strDirВ и®ӯз»ғж ·жң¬йӣҶзӣ®еҪ•В
- В В В В В *В @returnВ Map<String,Double>В cateWordsProbВ з”Ё"зұ»зӣ®_еҚ•иҜҚ"еҜ№жқҘзҙўеј•зҡ„map,дҝқеӯҳзҡ„valе°ұжҳҜиҜҘзұ»зӣ®дёӢиҜҘеҚ•иҜҚзҡ„еҮәзҺ°ж¬Ўж•°В
- В В В В В *В @throwsВ IOExceptionВ В
- В В В В В */В В
- В В В В publicВ Map<String,Double>В getCateWordsProb(StringВ strDir)В throwsВ IOException{В В
- В В В В В В В В Map<String,Double>В cateWordsProbВ =В newВ TreeMap<String,Double>();В В
- В В В В В В В В FileВ sampleFileВ =В newВ File(strDir);В В
- В В В В В В В В FileВ []В sampleDirВ =В sampleFile.listFiles();В В
- В В В В В В В В StringВ word;В В
- В В В В В В В В for(intВ iВ =В 0;iВ <В sampleDir.length;В i++){В В
- В В В В В В В В В В В В FileВ []В sampleВ =В sampleDir[i].listFiles();В В
- В В В В В В В В В В В В for(intВ jВ =В 0;В jВ <В sample.length;В j++){В В
- В В В В В В В В В В В В В В В В FileReaderВ samReaderВ =В newВ FileReader(sample[j]);В В
- В В В В В В В В В В В В В В В В BufferedReaderВ samBRВ =В newВ BufferedReader(samReader);В В
- В В В В В В В В В В В В В В В В while((wordВ =В samBR.readLine())В !=В null){В В
- В В В В В В В В В В В В В В В В В В В В StringВ keyВ =В sampleDir[i].getName()В +В "_"В +В word;В В
- В В В В В В В В В В В В В В В В В В В В if(cateWordsProb.containsKey(key)){В В
- В В В В В В В В В В В В В В В В В В В В В В В В doubleВ countВ =В cateWordsProb.get(key)В +В 1.0;В В
- В В В В В В В В В В В В В В В В В В В В В В В В cateWordsProb.put(key,В count);В В
- В В В В В В В В В В В В В В В В В В В В }В В
- В В В В В В В В В В В В В В В В В В В В elseВ {В В
- В В В В В В В В В В В В В В В В В В В В В В В В cateWordsProb.put(key,В 1.0);В В
- В В В В В В В В В В В В В В В В В В В В }В В
- В В В В В В В В В В В В В В В В }В В
- В В В В В В В В В В В В }В В
- В В В В В В В В }В В
- В В В В В В В В returnВ cateWordsProb;В В В В В
- В В В В }В В
- В В В В В В
- В В В В /**и®Ўз®—жҹҗдёҖдёӘжөӢиҜ•ж ·жң¬еұһдәҺжҹҗдёӘзұ»еҲ«зҡ„жҰӮзҺҮВ
- В В В В В *В @paramВ Map<String,В Double>В cateWordsProbВ и®°еҪ•жҜҸдёӘзӣ®еҪ•дёӯеҮәзҺ°зҡ„еҚ•иҜҚеҸҠж¬Ўж•°В В
- В В В В В *В @paramВ FileВ trainFileВ иҜҘзұ»еҲ«жүҖжңүзҡ„и®ӯз»ғж ·жң¬жүҖеңЁзӣ®еҪ•В
- В В В В В *В @paramВ Vector<String>В testFileWordsВ иҜҘжөӢиҜ•ж ·жң¬дёӯзҡ„жүҖжңүиҜҚжһ„жҲҗзҡ„е®№еҷЁВ
- В В В В В *В @paramВ doubleВ totalWordsNumВ и®°еҪ•жүҖжңүи®ӯз»ғж ·жң¬зҡ„еҚ•иҜҚжҖ»ж•°В
- В В В В В *В @paramВ Map<String,В Double>В cateWordsNumВ и®°еҪ•жҜҸдёӘзұ»еҲ«зҡ„еҚ•иҜҚжҖ»ж•°В
- В В В В В *В @returnВ BigDecimalВ иҝ”еӣһиҜҘжөӢиҜ•ж ·жң¬еңЁиҜҘзұ»еҲ«дёӯзҡ„жҰӮзҺҮВ
- В В В В В *В @throwsВ ExceptionВ В
- В В В В В *В @throwsВ IOExceptionВ В
- В В В В В */В В
- В В В В privateВ BigDecimalВ computeCateProb(FileВ trainFile,В Vector<String>В testFileWords,В Map<String,В Double>В cateWordsNum,В doubleВ totalWordsNum,В Map<String,В Double>В cateWordsProb)В throwsВ ExceptionВ {В В
- В В В В В В В В //В TODOВ Auto-generatedВ methodВ stubВ В
- В В В В В В В В BigDecimalВ probabilityВ =В newВ BigDecimal(1);В В
- В В В В В В В В doubleВ wordNumInCateВ =В cateWordsNum.get(trainFile.getName());В В
- В В В В В В В В BigDecimalВ wordNumInCateBDВ =В newВ BigDecimal(wordNumInCate);В В
- В В В В В В В В BigDecimalВ totalWordsNumBDВ =В newВ BigDecimal(totalWordsNum);В В
- В В В В В В В В for(Iterator<String>В itВ =В testFileWords.iterator();В it.hasNext();){В В
- В В В В В В В В В В В В StringВ meВ =В it.next();В В
- В В В В В В В В В В В В StringВ keyВ =В trainFile.getName()+"_"+me;В В
- В В В В В В В В В В В В doubleВ testFileWordNumInCate;В В
- В В В В В В В В В В В В if(cateWordsProb.containsKey(key)){В В
- В В В В В В В В В В В В В В В В testFileWordNumInCateВ =В cateWordsProb.get(key);В В
- В В В В В В В В В В В В }elseВ testFileWordNumInCateВ =В 0.0;В В
- В В В В В В В В В В В В BigDecimalВ testFileWordNumInCateBDВ =В newВ BigDecimal(testFileWordNumInCate);В В
- В В В В В В В В В В В В BigDecimalВ xcProbВ =В (testFileWordNumInCateBD.add(newВ BigDecimal(0.0001))).divide(totalWordsNumBD.add(wordNumInCateBD),10,В BigDecimal.ROUND_CEILING);В В
- В В В В В В В В В В В В probabilityВ =В probability.multiply(xcProb);В В
- В В В В В В В В }В В
- В В В В В В В В BigDecimalВ resВ =В probability.multiply(wordNumInCateBD.divide(totalWordsNumBD,10,В BigDecimal.ROUND_CEILING));В В
- В В В В В В В В returnВ res;В В
- В В В В }В В
- В В
- В В В В /**иҺ·еҫ—жҜҸдёӘзұ»зӣ®дёӢзҡ„еҚ•иҜҚжҖ»ж•°В
- В В В В В *В @paramВ trainDirВ и®ӯз»ғж–ҮжЎЈйӣҶзӣ®еҪ•В
- В В В В В *В @returnВ Map<String,В Double>В <зӣ®еҪ•еҗҚпјҢеҚ•иҜҚжҖ»ж•°>зҡ„mapВ
- В В В В В *В @throwsВ IOExceptionВ В
- В В В В В */В В
- В В В В privateВ Map<String,В Double>В getCateWordsNum(StringВ trainDir)В throwsВ IOExceptionВ {В В
- В В В В В В В В //В TODOВ Auto-generatedВ methodВ stubВ В
- В В В В В В В В Map<String,Double>В cateWordsNumВ =В newВ TreeMap<String,Double>();В В
- В В В В В В В В File[]В sampleDirВ =В newВ File(trainDir).listFiles();В В
- В В В В В В В В for(intВ iВ =В 0;В iВ <В sampleDir.length;В i++){В В
- В В В В В В В В В В В В doubleВ countВ =В 0;В В
- В В В В В В В В В В В В File[]В sampleВ =В sampleDir[i].listFiles();В В
- В В В В В В В В В В В В for(intВ jВ =В 0;jВ <В sample.length;В j++){В В
- В В В В В В В В В В В В В В В В FileReaderВ spReaderВ =В newВ FileReader(sample[j]);В В
- В В В В В В В В В В В В В В В В BufferedReaderВ spBRВ =В newВ BufferedReader(spReader);В В
- В В В В В В В В В В В В В В В В while(spBR.readLine()В !=В null){В В
- В В В В В В В В В В В В В В В В В В В В count++;В В
- В В В В В В В В В В В В В В В В }В В В В В В В В В
- В В В В В В В В В В В В }В В
- В В В В В В В В В В В В cateWordsNum.put(sampleDir[i].getName(),В count);В В
- В В В В В В В В }В В
- В В В В В В В В returnВ cateWordsNum;В В
- В В В В }В В
- В В В В В В
- В В В В /**ж №жҚ®жӯЈзЎ®зұ»зӣ®ж–Ү件е’ҢеҲҶзұ»з»“жһңж–Ү件з»ҹи®ЎеҮәеҮҶзЎ®зҺҮВ
- В В В В В *В @paramВ classifyResultFileВ жӯЈзЎ®зұ»зӣ®ж–Ү件В
- В В В В В *В @paramВ classifyResultFileNewВ еҲҶзұ»з»“жһңж–Ү件В
- В В В В В *В @returnВ doubleВ еҲҶзұ»зҡ„еҮҶзЎ®зҺҮВ
- В В В В В *В @throwsВ IOExceptionВ В
- В В В В В */В В
- В В В В doubleВ computeAccuracy(StringВ classifyResultFile,В В
- В В В В В В В В В В В В StringВ classifyResultFileNew)В throwsВ IOExceptionВ {В В
- В В В В В В В В //В TODOВ Auto-generatedВ methodВ stubВ В
- В В В В В В В В Map<String,String>В rightCateВ =В newВ TreeMap<String,String>();В В
- В В В В В В В В Map<String,String>В resultCateВ =В newВ TreeMap<String,String>();В В
- В В В В В В В В rightCateВ =В getMapFromResultFile(classifyResultFile);В В
- В В В В В В В В resultCateВ =В getMapFromResultFile(classifyResultFileNew);В В
- В В В В В В В В Set<Map.Entry<String,В String>>В resCateSetВ =В resultCate.entrySet();В В
- В В В В В В В В doubleВ rightCountВ =В 0.0;В В
- В В В В В В В В for(Iterator<Map.Entry<String,В String>>В itВ =В resCateSet.iterator();В it.hasNext();){В В
- В В В В В В В В В В В В Map.Entry<String,В String>В meВ =В it.next();В В
- В В В В В В В В В В В В if(me.getValue().equals(rightCate.get(me.getKey()))){В В
- В В В В В В В В В В В В В В В В rightCountВ ++;В В
- В В В В В В В В В В В В }В В
- В В В В В В В В }В В
- В В В В В В В В computerConfusionMatrix(rightCate,resultCate);В В
- В В В В В В В В returnВ rightCountВ /В resultCate.size();В В В В
- В В В В }В В
- В В В В В В
- В В В В /**ж №жҚ®жӯЈзЎ®зұ»зӣ®ж–Ү件е’ҢеҲҶзұ»з»“жһңж–Үи®Ўз®—ж··ж·Ҷзҹ©йҳө并且иҫ“еҮәВ
- В В В В В *В @paramВ rightCateВ жӯЈзЎ®зұ»зӣ®еҜ№еә”mapВ
- В В В В В *В @paramВ resultCateВ еҲҶзұ»з»“жһңеҜ№еә”mapВ
- В В В В В *В @returnВ doubleВ еҲҶзұ»зҡ„еҮҶзЎ®зҺҮВ
- В В В В В *В @throwsВ IOExceptionВ В
- В В В В В */В В
- В В В В privateВ voidВ computerConfusionMatrix(Map<String,В String>В rightCate,В В
- В В В В В В В В В В В В Map<String,В String>В resultCate)В {В В
- В В В В В В В В //В TODOВ Auto-generatedВ methodВ stubВ В В В
- В В В В В В В В int[][]В confusionMatrixВ =В newВ int[20][20];В В
- В В В В В В В В //йҰ–е…ҲжұӮеҮәзұ»зӣ®еҜ№еә”зҡ„ж•°з»„зҙўеј•В В
- В В В В В В В В SortedSet<String>В cateNamesВ =В newВ TreeSet<String>();В В
- В В В В В В В В Set<Map.Entry<String,В String>>В rightCateSetВ =В rightCate.entrySet();В В
- В В В В В В В В for(Iterator<Map.Entry<String,В String>>В itВ =В rightCateSet.iterator();В it.hasNext();){В В
- В В В В В В В В В В В В Map.Entry<String,В String>В meВ =В it.next();В В
- В В В В В В В В В В В В cateNames.add(me.getValue());В В
- В В В В В В В В }В В
- В В В В В В В В cateNames.add("rec.sport.baseball");//йҳІжӯўж•°е°‘дёҖдёӘзұ»зӣ®В В
- В В В В В В В В String[]В cateNamesArrayВ =В cateNames.toArray(newВ String[0]);В В
- В В В В В В В В Map<String,Integer>В cateNamesToIndexВ =В newВ TreeMap<String,Integer>();В В
- В В В В В В В В for(intВ iВ =В 0;В iВ <В cateNamesArray.length;В i++){В В
- В В В В В В В В В В В В cateNamesToIndex.put(cateNamesArray[i],i);В В
- В В В В В В В В }В В
- В В В В В В В В for(Iterator<Map.Entry<String,В String>>В itВ =В rightCateSet.iterator();В it.hasNext();){В В
- В В В В В В В В В В В В Map.Entry<String,В String>В meВ =В it.next();В В
- В В В В В В В В В В В В confusionMatrix[cateNamesToIndex.get(me.getValue())][cateNamesToIndex.get(resultCate.get(me.getKey()))]++;В В
- В В В В В В В В }В В
- В В В В В В В В //иҫ“еҮәж··ж·Ҷзҹ©йҳөВ В
- В В В В В В В В double[]В hangSumВ =В newВ double[20];В В
- В В В В В В В В System.out.print("В В В В ");В В
- В В В В В В В В for(intВ iВ =В 0;В iВ <В 20;В i++){В В
- В В В В В В В В В В В В System.out.print(iВ +В "В В В В ");В В
- В В В В В В В В }В В
- В В В В В В В В System.out.println();В В
- В В В В В В В В for(intВ iВ =В 0;В iВ <В 20;В i++){В В
- В В В В В В В В В В В В System.out.print(iВ +В "В В В В ");В В
- В В В В В В В В В В В В for(intВ jВ =В 0;В jВ <В 20;В j++){В В
- В В В В В В В В В В В В В В В В System.out.print(confusionMatrix[i][j]+"В В В В ");В В
- В В В В В В В В В В В В В В В В hangSum[i]В +=В confusionMatrix[i][j];В В
- В В В В В В В В В В В В }В В
- В В В В В В В В В В В В System.out.println(confusionMatrix[i][i]В /В hangSum[i]);В В
- В В В В В В В В }В В
- В В В В В В В В System.out.println();В В
- В В В В }В В
- В В
- В В В В /**д»ҺеҲҶзұ»з»“жһңж–Ү件дёӯиҜ»еҸ–mapВ
- В В В В В *В @paramВ classifyResultFileNewВ зұ»зӣ®ж–Ү件В
- В В В В В *В @returnВ Map<String,В String>В з”ұ<ж–Ү件еҗҚпјҢзұ»зӣ®еҗҚ>дҝқеӯҳзҡ„mapВ
- В В В В В *В @throwsВ IOExceptionВ В
- В В В В В */В В
- В В В В privateВ Map<String,В String>В getMapFromResultFile(В В
- В В В В В В В В В В В В StringВ classifyResultFileNew)В throwsВ IOExceptionВ {В В
- В В В В В В В В //В TODOВ Auto-generatedВ methodВ stubВ В
- В В В В В В В В FileВ crFileВ =В newВ File(classifyResultFileNew);В В
- В В В В В В В В FileReaderВ crReaderВ =В newВ FileReader(crFile);В В
- В В В В В В В В BufferedReaderВ crBRВ =В newВ BufferedReader(crReader);В В
- В В В В В В В В Map<String,В String>В resВ =В newВ TreeMap<String,В String>();В В
- В В В В В В В В String[]В s;В В
- В В В В В В В В StringВ line;В В
- В В В В В В В В while((lineВ =В crBR.readLine())В !=В null){В В
- В В В В В В В В В В В В sВ =В line.split("В ");В В
- В В В В В В В В В В В В res.put(s[0],В s[1]);В В В В В В
- В В В В В В В В }В В
- В В В В В В В В returnВ res;В В
- В В В В }В В
- В В
- В В В В /**В
- В В В В В *В @paramВ argsВ
- В В В В В *В @throwsВ ExceptionВ В
- В В В В В */В В
- В В В В publicВ voidВ NaiveBayesianClassifierMain(String[]В args)В throwsВ ExceptionВ {В В
- В В В В В В В В В //TODOВ Auto-generatedВ methodВ stubВ В
- В В В В В В В В //йҰ–е…ҲеҲӣе»әи®ӯз»ғйӣҶе’ҢжөӢиҜ•йӣҶВ В
- В В В В В В В В CreateTrainAndTestSampleВ cttВ =В newВ CreateTrainAndTestSample();В В
- В В В В В В В В NaiveBayesianClassifierВ nbClassifierВ =В newВ NaiveBayesianClassifier();В В
- В В В В В В В В ctt.filterSpecialWords();//ж №жҚ®еҢ…еҗ«йқһзү№еҫҒиҜҚзҡ„ж–ҮжЎЈйӣҶз”ҹжҲҗеҸӘеҢ…еҗ«зү№еҫҒиҜҚзҡ„ж–ҮжЎЈйӣҶеҲ°processedSampleOnlySpecialзӣ®еҪ•дёӢВ В
- В В В В В В В В double[]В accuracyOfEveryExpВ =В newВ double[10];В В
- В В В В В В В В doubleВ accuracyAvg,sumВ =В 0;В В
- В В В В В В В В for(intВ iВ =В 0;В iВ <В 10;В i++){//з”ЁдәӨеҸүйӘҢиҜҒжі•еҒҡеҚҒж¬ЎеҲҶзұ»е®һйӘҢпјҢеҜ№еҮҶзЎ®зҺҮеҸ–е№іеқҮеҖјВ В В
- В В В В В В В В В В В В StringВ TrainDirВ =В "F:/DataMiningSample/TrainSample"+i;В В
- В В В В В В В В В В В В StringВ TestDirВ =В "F:/DataMiningSample/TestSample"+i;В В
- В В В В В В В В В В В В StringВ classifyRightCateВ =В "F:/DataMiningSample/classifyRightCate"+i+".txt";В В
- В В В В В В В В В В В В StringВ classifyResultFileNewВ =В "F:/DataMiningSample/classifyResultNew"+i+".txt";В В
- В В В В В В В В В В В В ctt.createTestSamples("F:/DataMiningSample/processedSampleOnlySpecial",В 0.9,В i,classifyRightCate);В В
- В В В В В В В В В В В В nbClassifier.doProcess(TrainDir,TestDir,classifyResultFileNew);В В
- В В В В В В В В В В В В accuracyOfEveryExp[i]В =В nbClassifier.computeAccuracyВ (classifyRightCate,В classifyResultFileNew);В В
- В В В В В В В В В В В В System.out.println("TheВ accuracyВ forВ NaiveВ BayesianВ ClassifierВ inВ "+i+"thВ ExpВ isВ :"В +В accuracyOfEveryExp[i]);В В
- В В В В В В В В }В В
- В В В В В В В В for(intВ iВ =В 0;В iВ <В 10;В i++){В В
- В В В В В В В В В В В В sumВ +=В accuracyOfEveryExp[i];В В
- В В В В В В В В }В В
- В В В В В В В В accuracyAvgВ =В sumВ /В 10;В В
- В В В В В В В В System.out.println("TheВ averageВ accuracyВ forВ NaiveВ BayesianВ ClassifierВ inВ allВ ExpsВ isВ :"В +В accuracyAvg);В В
- В В В В В В В В В В
- В В В В }В В
- }В В
В
В
2.7.4гҖҒжңҙзҙ иҙқеҸ¶ж–Ҝз®—жі•еҜ№newsgroupж–ҮжЎЈйӣҶеҒҡеҲҶзұ»зҡ„з»“жһң

В
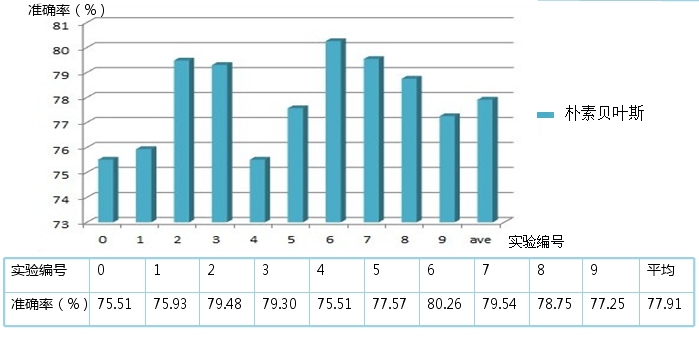
В В еҸ–жүҖжңүиҜҚе…ұ87554дёӘдҪңдёәзү№еҫҒиҜҚпјҡ10ж¬ЎдәӨеҸүйӘҢиҜҒе®һйӘҢе№іеқҮеҮҶзЎ®зҺҮ78.19%пјҢз”Ёж—¶23min,еҮҶзЎ®зҺҮиҢғеӣҙ75.65%-80.47%пјҢ第6ж¬Ўе®һйӘҢеҮҶзЎ®зҺҮи¶…иҝҮ80%пјҢеҸ–еҮәзҺ°ж¬Ўж•°еӨ§дәҺзӯүдәҺ4ж¬Ўзҡ„иҜҚе…ұи®Ў30095дёӘдҪңдёәзү№еҫҒиҜҚпјҡ 10ж¬ЎдәӨеҸүйӘҢиҜҒе®һйӘҢе№іеқҮеҮҶзЎ®зҺҮ77.91%пјҢз”Ёж—¶22minпјҢеҮҶзЎ®зҺҮиҢғеӣҙ75.51%-80.26%пјҢ第6ж¬Ўе®һйӘҢеҮҶзЎ®зҺҮи¶…иҝҮ80%гҖӮеҰӮдёӢеӣҫжүҖзӨәпјҡ
В
2.7.5гҖҒиҙқеҸ¶ж–Ҝз®—жі•зҡ„ж”№иҝӣ
- дјҳеҢ–зү№еҫҒиҜҚзҡ„йҖүеҸ–зӯ–з•Ҙпјӣ
- ж”№иҝӣеӨҡйЎ№ејҸжЁЎеһӢзҡ„зұ»жқЎд»¶жҰӮзҺҮзҡ„и®Ўз®—е…¬ејҸпјҢж”№иҝӣдёәВ зұ»жқЎд»¶жҰӮзҺҮP(tk|c)=(зұ»cдёӢеҚ•иҜҚtkеңЁеҗ„дёӘж–ҮжЎЈдёӯеҮәзҺ°иҝҮзҡ„ж¬Ўж•°д№Ӣе’Ң+0.001)/пјҲзұ»cдёӢеҚ•иҜҚжҖ»ж•°+и®ӯз»ғж ·жң¬дёӯдёҚйҮҚеӨҚзү№еҫҒиҜҚжҖ»ж•°пјүпјҢеҲҶеӯҗеҪ“tkжІЎжңүеҮәзҺ°ж—¶пјҢеҸӘеҠ 0.001(д№ӢеүҚдёҠйқў2.7.3иҠӮжҳҜ+1)пјҢиҝҷж ·жӣҙеҠ зІҫзЎ®зҡ„жҸҸиҝ°зҡ„иҜҚзҡ„з»ҹи®ЎеҲҶеёғ规еҫӢпјҢ

В
В
В
第дёүйғЁеҲҶгҖҒд»ҺEMз®—жі•еҲ°йҡҗ马еҸҜеӨ«жЁЎеһӢпјҲHMMпјү
В
3.1гҖҒEMВ з®—жі•дёҺеҹәдәҺжЁЎеһӢзҡ„иҒҡзұ»
В В В еңЁз»ҹи®Ўи®Ўз®—дёӯпјҢжңҖеӨ§жңҹжңӣ пјҲEMпјҢExpectationвҖ“Maximizationпјүз®—жі•жҳҜеңЁжҰӮзҺҮпјҲprobabilisticпјүжЁЎеһӢдёӯеҜ»жүҫеҸӮж•°жңҖеӨ§дјјз„¶дј°и®Ўзҡ„з®—жі•пјҢе…¶дёӯжҰӮзҺҮжЁЎеһӢдҫқиө–дәҺж— жі•и§ӮжөӢзҡ„йҡҗи—ҸеҸҳйҮҸпјҲLatent VariablпјүгҖӮжңҖеӨ§жңҹжңӣз»Ҹеёёз”ЁеңЁжңәеҷЁеӯҰд№ е’Ңи®Ўз®—жңәи§Ҷи§үзҡ„ж•°жҚ®йӣҶиҒҡпјҲData ClusteringпјүйўҶеҹҹгҖӮ
В В йҖҡеёёжқҘиҜҙпјҢиҒҡзұ»жҳҜдёҖз§Қж— жҢҮеҜјзҡ„жңәеҷЁеӯҰд№ й—®йўҳпјҢеҰӮжӯӨй—®йўҳжҸҸиҝ°пјҡз»ҷдҪ дёҖе Ҷж•°жҚ®зӮ№пјҢи®©дҪ е°Ҷе®ғ们жңҖйқ и°ұең°еҲҶжҲҗдёҖе ҶдёҖе Ҷзҡ„гҖӮиҒҡзұ»з®—жі•еҫҲеӨҡпјҢдёҚеҗҢзҡ„з®—жі•йҖӮеә”дәҺдёҚеҗҢзҡ„й—®йўҳпјҢиҝҷйҮҢд»…д»Ӣз»ҚдёҖдёӘеҹәдәҺжЁЎеһӢзҡ„иҒҡзұ»пјҢиҜҘиҒҡзұ»з®—жі•еҜ№ж•°жҚ®зӮ№зҡ„еҒҮи®ҫжҳҜпјҢиҝҷдәӣж•°жҚ®зӮ№еҲҶеҲ«жҳҜеӣҙз»• K дёӘж ёеҝғзҡ„ K дёӘжӯЈжҖҒеҲҶеёғжәҗжүҖйҡҸжңәз”ҹжҲҗзҡ„пјҢдҪҝз”Ё Han JiaWei зҡ„гҖҠData Mingпјҡ Concepts and TechniquesгҖӢдёӯзҡ„еӣҫпјҡ
В
В
В
В
В В еӣҫдёӯжңүдёӨдёӘжӯЈжҖҒеҲҶеёғж ёеҝғпјҢз”ҹжҲҗдәҶеӨ§иҮҙдёӨе ҶзӮ№гҖӮжҲ‘们зҡ„иҒҡзұ»з®—жі•е°ұжҳҜйңҖиҰҒж №жҚ®з»ҷеҮәжқҘзҡ„йӮЈдәӣзӮ№пјҢз®—еҮәиҝҷдёӨдёӘжӯЈжҖҒеҲҶеёғзҡ„ж ёеҝғеңЁд»Җд№ҲдҪҚзҪ®пјҢд»ҘеҸҠеҲҶеёғзҡ„еҸӮж•°жҳҜеӨҡе°‘гҖӮиҝҷеҫҲжҳҺжҳҫеҸҲжҳҜдёҖдёӘиҙқеҸ¶ж–Ҝй—®йўҳпјҢдҪҶиҝҷж¬ЎдёҚеҗҢзҡ„жҳҜпјҢзӯ”жЎҲжҳҜиҝһз»ӯзҡ„дё”жңүж— з©·еӨҡз§ҚеҸҜиғҪжҖ§пјҢжӣҙзіҹзҡ„жҳҜпјҢеҸӘжңүеҪ“жҲ‘们зҹҘйҒ“дәҶе“ӘдәӣзӮ№еұһдәҺеҗҢдёҖдёӘжӯЈжҖҒеҲҶеёғеңҲзҡ„ж—¶еҖҷжүҚиғҪеӨҹеҜ№иҝҷдёӘеҲҶеёғзҡ„еҸӮж•°дҪңеҮәйқ и°ұзҡ„йў„жөӢпјҢзҺ°еңЁдёӨе ҶзӮ№ж··еңЁдёҖеқ—жҲ‘们еҸҲдёҚзҹҘйҒ“е“ӘдәӣзӮ№еұһдәҺ第дёҖдёӘжӯЈжҖҒеҲҶеёғпјҢе“ӘдәӣеұһдәҺ第дәҢдёӘгҖӮеҸҚиҝҮжқҘпјҢеҸӘжңүеҪ“жҲ‘们еҜ№еҲҶеёғзҡ„еҸӮж•°дҪңеҮәдәҶйқ и°ұзҡ„йў„жөӢж—¶еҖҷпјҢжүҚиғҪзҹҘйҒ“еҲ°еә•е“ӘдәӣзӮ№еұһдәҺ第дёҖдёӘеҲҶеёғпјҢйӮЈдәӣзӮ№еұһдәҺ第дәҢдёӘеҲҶеёғгҖӮиҝҷе°ұжҲҗдәҶдёҖдёӘе…ҲжңүйёЎиҝҳжҳҜе…ҲжңүиӣӢзҡ„й—®йўҳдәҶгҖӮдёәдәҶи§ЈеҶіиҝҷдёӘеҫӘзҺҜдҫқиө–пјҢжҖ»жңүдёҖж–№иҰҒе…Ҳжү“з ҙеғөеұҖпјҢиҜҙпјҢдёҚз®ЎдәҶпјҢжҲ‘е…ҲйҡҸдҫҝж•ҙдёҖдёӘеҖјеҮәжқҘпјҢзңӢдҪ жҖҺд№ҲеҸҳпјҢ然еҗҺжҲ‘еҶҚж №жҚ®дҪ зҡ„еҸҳеҢ–и°ғж•ҙжҲ‘зҡ„еҸҳеҢ–пјҢ然еҗҺеҰӮжӯӨиҝӯд»ЈзқҖдёҚж–ӯдә’зӣёжҺЁеҜјпјҢжңҖз»Ҳ收ж•ӣеҲ°дёҖдёӘи§ЈгҖӮиҝҷе°ұжҳҜ EM з®—жі•гҖӮ
В В EM зҡ„ж„ҸжҖқжҳҜвҖңExpectation-MaximazationвҖқпјҢеңЁиҝҷдёӘиҒҡзұ»й—®йўҳйҮҢйқўпјҢжҲ‘们жҳҜе…ҲйҡҸдҫҝзҢңдёҖдёӢиҝҷдёӨдёӘжӯЈжҖҒеҲҶеёғзҡ„еҸӮж•°пјҡеҰӮж ёеҝғеңЁд»Җд№Ҳең°ж–№пјҢж–№е·®жҳҜеӨҡе°‘гҖӮ然еҗҺи®Ўз®—еҮәжҜҸдёӘж•°жҚ®зӮ№жӣҙеҸҜиғҪеұһдәҺ第дёҖдёӘиҝҳжҳҜ第дәҢдёӘжӯЈжҖҒеҲҶеёғеңҲпјҢиҝҷдёӘжҳҜеұһдәҺ Expectation дёҖжӯҘгҖӮжңүдәҶжҜҸдёӘж•°жҚ®зӮ№зҡ„еҪ’еұһпјҢжҲ‘们е°ұеҸҜд»Ҙж №жҚ®еұһдәҺ第дёҖдёӘеҲҶеёғзҡ„ж•°жҚ®зӮ№жқҘйҮҚж–°иҜ„估第дёҖдёӘеҲҶеёғзҡ„еҸӮж•°пјҲд»ҺиӣӢеҶҚеӣһеҲ°йёЎпјүпјҢиҝҷдёӘжҳҜ Maximazation гҖӮеҰӮжӯӨеҫҖеӨҚпјҢзӣҙеҲ°еҸӮж•°еҹәжң¬дёҚеҶҚеҸ‘з”ҹеҸҳеҢ–дёәжӯўгҖӮиҝҷдёӘиҝӯ代收ж•ӣиҝҮзЁӢдёӯзҡ„иҙқеҸ¶ж–Ҝж–№жі•еңЁз¬¬дәҢжӯҘпјҢж №жҚ®ж•°жҚ®зӮ№жұӮеҲҶеёғзҡ„еҸӮж•°дёҠйқўгҖӮ
3.2гҖҒйҡҗ马еҸҜеӨ«жЁЎеһӢпјҲHMMпјү
В В еӨ§еӨҡзҡ„д№ҰзұҚжҲ–и®әж–ҮйғҪи®ІдёҚжё…жҘҡиҝҷдёӘйҡҗ马еҸҜеӨ«жЁЎеһӢ(HMM)пјҢеҢ…жӢ¬жңӘй№Ҹе…„д№ӢеҺҹж–Үд№ҹи®Іеҫ—дёҚеӨҹе…·дҪ“жҳҺзҷҪгҖӮжҺҘдёӢжқҘпјҢжҲ‘е°ҪйҮҸз”ЁзӣҙзҷҪжҳ“жҮӮзҡ„иҜӯиЁҖйҳҗиҝ°иҝҷдёӘжЁЎеһӢгҖӮ然еңЁд»Ӣз»Қйҡҗ马еҸҜеӨ«жЁЎеһӢд№ӢеүҚпјҢжңүеҝ…иҰҒе…ҲиЎҢд»Ӣз»ҚдёӢеҚ•зәҜзҡ„马еҸҜеӨ«жЁЎеһӢ(жң¬иҠӮдё»иҰҒеј•з”Ёпјҡз»ҹи®ЎиҮӘ然иҜӯиЁҖеӨ„зҗҶпјҢе®—жҲҗеәҶзј–и‘—дёҖд№ҰдёҠзҡ„зӣёе…іеҶ…е®№)гҖӮ
3.2.1гҖҒ马еҸҜеӨ«жЁЎеһӢ
В В жҲ‘们зҹҘйҒ“пјҢйҡҸжңәиҝҮзЁӢеҸҲз§°йҡҸжңәеҮҪж•°пјҢжҳҜйҡҸж—¶й—ҙиҖҢйҡҸжңәеҸҳеҢ–зҡ„иҝҮзЁӢгҖӮ马еҸҜеӨ«жЁЎеһӢдҫҝжҳҜжҸҸиҝ°дәҶдёҖзұ»йҮҚиҰҒзҡ„йҡҸжңәиҝҮзЁӢгҖӮжҲ‘们常常йңҖиҰҒиҖғеҜҹдёҖдёӘйҡҸжңәеҸҳйҮҸеәҸеҲ—пјҢиҝҷдәӣйҡҸжңәеҸҳйҮҸ并дёҚжҳҜзӣёдә’зӢ¬з«Ӣзҡ„(жіЁж„ҸпјҡзҗҶи§ЈиҝҷдёӘйқһзӣёдә’зӢ¬з«ӢпјҢеҚізӣёдә’д№Ӣй—ҙжңүеҚғдёқдёҮзј•зҡ„иҒ”зі»)гҖӮ
В В еҰӮжһңжӯӨж—¶пјҢжҲ‘д№ҹжҗһдёҖеӨ§жҺЁзҠ¶жҖҒж–№зЁӢејҸпјҢжҒҗжҖ•жҲ‘д№ҹеҫҲйҡҫйҖғи„ұи¶Ҡи®Іи¶ҠеӨҚжқӮзҡ„жҖӘеңҲдәҶгҖӮжүҖд»ҘпјҢзӣҙжҺҘдёҫдҫӢеӯҗеҗ§пјҢеҰӮпјҢдёҖж®өж–Үеӯ—дёӯеҗҚиҜҚгҖҒеҠЁиҜҚгҖҒеҪўе®№иҜҚдёүзұ»иҜҚжҖ§еҮәзҺ°зҡ„жғ…еҶөеҸҜз”ұдёүдёӘзҠ¶жҖҒзҡ„马尔科еӨ«жЁЎеһӢжҸҸиҝ°еҰӮдёӢпјҡ
В
зҠ¶жҖҒs1пјҡеҗҚиҜҚ
зҠ¶жҖҒs2пјҡеҠЁиҜҚ
зҠ¶жҖҒs3пјҡеҪўе®№иҜҚ
В
еҒҮи®ҫзҠ¶жҖҒд№Ӣй—ҙзҡ„иҪ¬з§»зҹ©йҳөеҰӮдёӢпјҡ
В
В В В В В В В В В В В В В В В В s1В В s2 В В s3
В В В В В В В В В В В В s1 В 0.3 В В В 0.5 В В 0.2
В В A = [aij] = В В s2 В 0.5 В В В 0.3 В В 0.2
В В В В В В В В В В В В s3 В 0.4 В В В 0.2 В В 0.4
В
В В еҰӮжһңеңЁиҜҘж®өж–Үеӯ—дёӯжҹҗдёҖдёӘеҸҘеӯҗзҡ„第дёҖдёӘиҜҚдёәеҗҚиҜҚпјҢйӮЈд№Ҳж №жҚ®иҝҷдёҖжЁЎеһӢMпјҢеңЁиҜҘеҸҘеӯҗдёӯиҝҷдёүзұ»иҜҚеҮәзҺ°йЎәеәҸдёәO="еҗҚеҠЁеҪўеҗҚвҖқзҡ„жҰӮзҺҮдёәпјҡ
В В P(O|M)=P(s1пјҢs2пјҢs3пјҢs1 | M) = P(s1) Г—гҖҖP(s2 | s1) * P(s3 | s2)*P(s1 | s3)
В В В В В В В В =1* a12 * a23 * a31=0.5*0.2*0.4=0.004
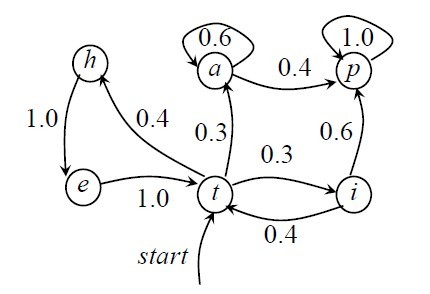
  马尔еҸҜеӨ«жЁЎеһӢеҸҲеҸҜи§ҶдёәйҡҸжңәзҡ„жңүйҷҗзҠ¶жҖҒжңәгҖӮ马尔жҹҜеӨ«й“ҫеҸҜд»ҘиЎЁзӨәжҲҗзҠ¶жҖҒеӣҫпјҲиҪ¬з§»еј§дёҠжңүжҰӮзҺҮзҡ„йқһзЎ®е®ҡзҡ„жңүйҷҗзҠ¶жҖҒиҮӘеҠЁжңәпјүпјҢеҰӮдёӢеӣҫжүҖзӨәпјҢ
В В еңЁдёҠеӣҫдёӯпјҢеңҶеңҲиЎЁзӨәзҠ¶жҖҒпјҢзҠ¶жҖҒд№Ӣй—ҙзҡ„иҪ¬з§»з”ЁеёҰз®ӯеӨҙзҡ„еј§иЎЁзӨәпјҢеј§дёҠзҡ„ж•°еӯ—дёәзҠ¶жҖҒиҪ¬з§»зҡ„жҰӮзҺҮпјҢеҲқе§ӢзҠ¶жҖҒз”Ёж Үи®°дёәstartзҡ„иҫ“е…Ҙз®ӯеӨҙиЎЁзӨәпјҢеҒҮи®ҫд»»дҪ•зҠ¶жҖҒйғҪеҸҜдҪңдёәз»ҲжӯўзҠ¶жҖҒгҖӮеӣҫдёӯйӣ¶жҰӮзҺҮзҡ„иҪ¬з§»еј§зңҒз•ҘпјҢдё”жҜҸдёӘиҠӮзӮ№дёҠжүҖжңүеҸ‘еҮәеј§зҡ„жҰӮзҺҮд№Ӣе’ҢзӯүдәҺ1гҖӮд»ҺдёҠеӣҫеҸҜд»ҘзңӢеҮәпјҢ马尔еҸҜеӨ«жЁЎеһӢеҸҜд»ҘзңӢеҒҡжҳҜдёҖдёӘиҪ¬з§»еј§дёҠжңүжҰӮзҺҮзҡ„йқһзЎ®е®ҡзҡ„жңүйҷҗзҠ¶жҖҒиҮӘеҠЁжңәгҖӮ
3.2.2гҖҒйҡҗ马еҸҜеӨ«жЁЎеһӢ(HMM)
В В еңЁдёҠж–Үд»Ӣз»Қзҡ„马еҸҜеӨ«жЁЎеһӢдёӯпјҢжҜҸдёӘзҠ¶жҖҒд»ЈиЎЁдәҶдёҖдёӘеҸҜи§ӮеҜҹзҡ„дәӢ件пјҢжүҖд»ҘпјҢ马еҸҜеӨ«жЁЎеһӢжңүж—¶еҸҲз§°дҪңи§Ҷ马еҸҜеӨ«жЁЎеһӢ(VMM)пјҢиҝҷеңЁжҹҗз§ҚзЁӢеәҰдёҠйҷҗеҲ¶дәҶжЁЎеһӢзҡ„йҖӮеә”жҖ§гҖӮиҖҢеңЁжҲ‘们зҡ„йҡҗ马еҸҜеӨ«жЁЎеһӢ(HMM)дёӯпјҢжҲ‘们дёҚзҹҘйҒ“жЁЎеһӢжүҖз»ҸиҝҮзҡ„зҠ¶жҖҒеәҸеҲ—пјҢеҸӘзҹҘйҒ“зҠ¶жҖҒзҡ„жҰӮзҺҮеҮҪж•°пјҢд№ҹе°ұжҳҜиҜҙпјҢи§ӮеҜҹеҲ°зҡ„дәӢ件жҳҜзҠ¶жҖҒзҡ„йҡҸжңәеҮҪж•°пјҢеӣ жӯӨж”№жЁЎеһӢжҳҜдёҖдёӘеҸҢйҮҚзҡ„йҡҸжңәиҝҮзЁӢгҖӮе…¶дёӯпјҢжЁЎеһӢзҡ„зҠ¶жҖҒиҪ¬жҚўжҳҜдёҚеҸҜи§ӮеҜҹзҡ„пјҢеҚійҡҗи”Ҫзҡ„пјҢеҸҜи§ӮеҜҹдәӢ件зҡ„йҡҸжңәиҝҮзЁӢжҳҜйҡҗи”Ҫзҡ„зҠ¶жҖҒиҝҮзЁӢзҡ„йҡҸжңәеҮҪж•°гҖӮ
В В В
В В зҗҶи®әеӨҡиҜҙж— зӣҠпјҢжҺҘдёӢжқҘпјҢз•ҷдёӘжҖқиҖғйўҳз»ҷиҜ»иҖ…пјҡN дёӘиўӢеӯҗпјҢжҜҸдёӘиўӢеӯҗдёӯжңүM з§ҚдёҚеҗҢйўңиүІзҡ„зҗғгҖӮдёҖе®һйӘҢе‘ҳж №жҚ®жҹҗдёҖжҰӮзҺҮеҲҶеёғйҖүжӢ©дёҖдёӘиўӢеӯҗпјҢ然еҗҺж №жҚ®иўӢеӯҗдёӯдёҚеҗҢйўңиүІзҗғзҡ„жҰӮзҺҮеҲҶеёғйҡҸжңәеҸ–еҮәдёҖдёӘзҗғпјҢ并жҠҘе‘ҠиҜҘзҗғзҡ„йўңиүІгҖӮеҜ№еұҖеӨ–дәәпјҡеҸҜи§ӮеҜҹзҡ„иҝҮзЁӢжҳҜдёҚеҗҢйўңиүІзҗғзҡ„еәҸеҲ—пјҢиҖҢиўӢеӯҗзҡ„еәҸеҲ—жҳҜдёҚеҸҜи§ӮеҜҹзҡ„гҖӮжҜҸеҸӘиўӢеӯҗеҜ№еә”HMMдёӯзҡ„дёҖдёӘзҠ¶жҖҒпјӣзҗғзҡ„йўңиүІеҜ№еә”дәҺHMM дёӯзҠ¶жҖҒзҡ„иҫ“еҮәгҖӮ
3.2.2гҖҒHMMеңЁдёӯж–ҮеҲҶиҜҚгҖҒжңәеҷЁзҝ»иҜ‘зӯүж–№йқўзҡ„е…·дҪ“еә”з”Ё
В В В йҡҗ马еҸҜеӨ«жЁЎеһӢеңЁеҫҲеӨҡж–№йқўйғҪжңүзқҖе…·дҪ“зҡ„еә”з”ЁпјҢеҰӮз”ұдәҺйҡҗ马еҸҜеӨ«жЁЎеһӢHMMжҸҗдҫӣдәҶдёҖдёӘеҸҜд»Ҙз»јеҗҲеҲ©з”ЁеӨҡз§ҚиҜӯиЁҖдҝЎжҒҜзҡ„з»ҹи®ЎжЎҶжһ¶пјҢеӣ жӯӨпјҢжҲ‘们е®Ңе…ЁеҸҜд»Ҙи®ІжұүиҜӯиҮӘеҠЁеҲҶиҜҚдёҺиҜҚжҖ§ж ҮжіЁз»ҹдёҖиҖғеҜҹпјҢе»әз«ӢеҹәдәҺHMMзҡ„еҲҶиҜҚдёҺиҜҚжҖ§ж ҮжіЁзҡ„дёҖдҪ“еҢ–зі»з»ҹгҖӮ
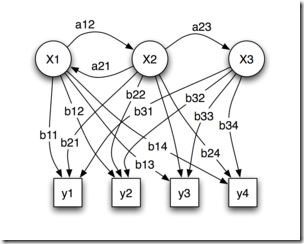
В В ж №жҚ®дёҠж–ҮеҜ№HMMзҡ„д»Ӣз»ҚпјҢдёҖдёӘHMMйҖҡеёёеҸҜд»ҘзңӢеҒҡз”ұдёӨйғЁеҲҶз»„жҲҗпјҡдёҖдёӘжҳҜзҠ¶жҖҒиҪ¬з§»жЁЎеһӢпјҢдёҖдёӘжҳҜзҠ¶жҖҒеҲ°и§ӮеҜҹеәҸеҲ—зҡ„з”ҹжҲҗжЁЎеһӢгҖӮе…·дҪ“еҲ°дёӯж–ҮеҲҶиҜҚиҝҷдёҖй—®йўҳдёӯпјҢеҸҜд»ҘжҠҠжұүеӯ—дёІжҲ–еҸҘеӯҗSдҪңдёәиҫ“е…ҘпјҢеҚ•иҜҚдёІSwдёәзҠ¶жҖҒзҡ„иҫ“еҮәпјҢеҚіи§ӮеҜҹеәҸеҲ—пјҢSw=w1w2w3...wN(N>=1)пјҢиҜҚжҖ§еәҸеҲ—StдёәзҠ¶жҖҒеәҸеҲ—пјҢжҜҸдёӘиҜҚжҖ§ж Үи®°ctеҜ№еә”HMMдёӯзҡ„дёҖдёӘзҠ¶жҖҒqiпјҢSc=c1c2c3...cnгҖӮ
В В йӮЈд№ҲпјҢеҲ©з”ЁHMMеӨ„зҗҶй—®йўҳй—®йўҳжҒ°еҘҪеҜ№еә”дәҺи§ЈеҶіHMMзҡ„дёүдёӘеҹәжң¬й—®йўҳпјҡ
В
- дј°и®ЎжЁЎеһӢзҡ„еҸӮж•°пјӣ
- еҜ№дәҺдёҖдёӘз»ҷе®ҡзҡ„иҫ“е…ҘSеҸҠе…¶еҸҜиғҪзҡ„иҫ“еҮәеәҸеҲ—Swе’ҢжЁЎеһӢu=(AпјҢBпјҢ*)пјҢеҝ«йҖҹең°и®Ўз®—P(Sw|u)пјҢжүҖжңүеҸҜиғҪзҡ„SwдёӯдҪҝжҰӮзҺҮP(Sw|u)жңҖеӨ§зҡ„и§Је°ұжҳҜиҰҒжүҫзҡ„еҲҶиҜҚж•Ҳжһңпјӣ
- еҝ«йҖҹең°йҖүжӢ©жңҖдјҳзҡ„зҠ¶жҖҒеәҸеҲ—жҲ–иҜҚжҖ§еәҸеҲ—пјҢдҪҝе…¶жңҖеҘҪең°и§ЈйҮҠи§ӮеҜҹеәҸеҲ—гҖӮ













зӣёе…іжҺЁиҚҗ
ж Үйўҳдёӯзҡ„вҖңиҙқеҸ¶ж–ҜеҲҶзұ»вҖқжҳҜжҢҮдёҖз§ҚеҹәдәҺиҙқеҸ¶ж–Ҝе®ҡзҗҶзҡ„з»ҹи®ЎеҲҶзұ»ж–№жі•пјҢе®ғеңЁжңәеҷЁеӯҰд№ йўҶеҹҹе№ҝжіӣеә”з”ЁгҖӮиҙқеҸ¶ж–ҜеҲҶзұ»еҷЁйҖҡиҝҮе…ҲйӘҢжҰӮзҺҮе’ҢжқЎд»¶жҰӮзҺҮжқҘйў„жөӢж–°е®һдҫӢзҡ„зұ»еҲ«пјҢе°Өе…¶йҖӮеҗҲеӨ„зҗҶй«ҳз»ҙзЁҖз–Ҹж•°жҚ®гҖӮеңЁиҝҷдёӘжЎҲдҫӢдёӯпјҢжҲ‘们е°ҶдҪҝз”ЁPythonиҜӯиЁҖ...
гҖҗдҪңе“ҒеҗҚз§°гҖ‘пјҡеҹәдәҺmatlabзҡ„иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁи®ҫи®ЎпјҢеҢ…еҗ«жңҖе°Ҹй”ҷиҜҜзҺҮиҙқеҸ¶ж–ҜеҲҶзұ»еҷЁгҖҒжңҖе°ҸйЈҺйҷ©иҙқеҸ¶ж–ҜеҶізӯ–пјҲеҗ«и®Ўз®—иҝҮзЁӢ е’Ң е®һйӘҢз»“жһңпјү гҖҗйҖӮз”ЁдәәзҫӨгҖ‘пјҡйҖӮз”ЁдәҺеёҢжңӣеӯҰд№ дёҚеҗҢжҠҖжңҜйўҶеҹҹзҡ„е°ҸзҷҪжҲ–иҝӣйҳ¶еӯҰд№ иҖ…гҖӮеҸҜдҪңдёәжҜ•и®ҫйЎ№зӣ®гҖҒиҜҫзЁӢ...
**еҹәдәҺиҙқеҸ¶ж–ҜеҲҶзұ»еҷЁзҡ„ж•°жҚ®еӨ„зҗҶдёҺMATLABе®һзҺ°** еңЁж•°жҚ®з§‘еӯҰйўҶеҹҹпјҢеҲҶзұ»й—®йўҳжҳҜдёҖз§Қеёёи§Ғзҡ„д»»еҠЎпјҢе®ғж¶үеҸҠе°Ҷж•°жҚ®ж ·жң¬еҲҶй…ҚеҲ°йў„е®ҡд№үзҡ„зұ»еҲ«дёӯгҖӮе…¶дёӯпјҢиҙқеҸ¶ж–ҜеҲҶзұ»еҷЁжҳҜдёҖз§Қе№ҝжіӣеә”з”Ёзҡ„з®—жі•пјҢе°Өе…¶йҖӮз”ЁдәҺеӨ„зҗҶй«ҳз»ҙж•°жҚ®е’ҢеӨ§йҮҸзү№еҫҒзҡ„...
иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁжҳҜдёҖз§ҚеҹәдәҺжҰӮзҺҮзҗҶи®әзҡ„жңәеҷЁеӯҰд№ ж–№жі•пјҢе®ғеҲ©з”ЁиҙқеҸ¶ж–Ҝе®ҡзҗҶжқҘйў„жөӢдёҖдёӘе®һдҫӢеұһдәҺжҹҗдёӘзұ»еҲ«зҡ„жҰӮзҺҮгҖӮеңЁжң¬жЎҲдҫӢдёӯпјҢжҲ‘们关注зҡ„жҳҜеҰӮдҪ•еңЁMATLABзҺҜеўғдёӯе®һзҺ°иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁпјҢ并йҖҡиҝҮвҖңзӢјжқҘдәҶвҖқзҡ„еҜ“иЁҖж•…дәӢжқҘйҳҗиҝ°е…¶еә”з”ЁгҖӮиҝҷдёӘ...
иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁжҳҜдёҖз§ҚеҹәдәҺжҰӮзҺҮзҗҶи®әзҡ„з»ҹи®ЎеӯҰд№ ж–№жі•пјҢе®ғеңЁжңәеҷЁеӯҰд№ йўҶеҹҹжңүзқҖе№ҝжіӣзҡ„еә”з”ЁгҖӮеңЁMATLABдёӯпјҢжҲ‘们еҸҜд»ҘеҲ©з”Ёе…¶ејәеӨ§зҡ„ж•°еӯҰи®Ўз®—иғҪеҠӣе’Ңдё°еҜҢзҡ„еҮҪж•°еә“жқҘе®һзҺ°иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁгҖӮдёӢйқўе°ҶиҜҰз»Ҷд»Ӣз»ҚиҙқеҸ¶ж–ҜеҲҶзұ»еҷЁзҡ„еҹәжң¬еҺҹзҗҶгҖҒMATLAB...
ж №жҚ®жҸҗдҫӣзҡ„ж–Ү件дҝЎжҒҜпјҢжҲ‘们еҸҜд»Ҙж·ұе…ҘжҺўи®ЁиҙқеҸ¶ж–ҜеҲҶзұ»еҷЁеңЁMATLABдёӯзҡ„е®һзҺ°еҺҹзҗҶеҸҠе…·дҪ“еә”з”Ёз»ҶиҠӮгҖӮиҝҷж®өд»Јз Ғеұ•зӨәдәҶеҰӮдҪ•дҪҝз”ЁиҙқеҸ¶ж–ҜеҲҶзұ»еҷЁиҝӣиЎҢеӨҡзұ»еҲ«еҲҶзұ»пјҢ并йҖҡиҝҮеӨҡж¬ЎжЁЎжӢҹе®һйӘҢжқҘжҸҗй«ҳжөӢиҜ•зІҫеәҰгҖӮ ### иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁз®Җд»Ӣ иҙқеҸ¶ж–Ҝ...
гҖҠеҹәдәҺMATLABзҡ„иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁи®ҫи®ЎгҖӢ еңЁдҝЎжҒҜжҠҖжңҜйўҶеҹҹпјҢжЁЎејҸиҜҶеҲ«жҳҜйҮҚиҰҒзҡ„з ”з©¶ж–№еҗ‘пјҢиҖҢиҙқеҸ¶ж–ҜеҲҶзұ»еҷЁеҲҷжҳҜе®һзҺ°иҝҷдёҖзӣ®ж Үзҡ„жңүж•Ҳе·Ҙе…·гҖӮMATLABдҪңдёәдёҖз§ҚејәеӨ§зҡ„ж•°еҖји®Ўз®—е’Ңзј–зЁӢзҺҜеўғпјҢеёёиў«з”ЁжқҘе®һзҺ°еҗ„з§Қз®—жі•пјҢеҢ…жӢ¬жңҙзҙ иҙқеҸ¶ж–Ҝз®—жі•гҖӮ...
жңҙзҙ иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁжҳҜдёҖз§ҚеҹәдәҺжҰӮзҺҮзҡ„жңәеҷЁеӯҰд№ з®—жі•пјҢе®ғеҹәдәҺиҙқеҸ¶ж–Ҝе®ҡзҗҶе’Ңзү№еҫҒжқЎд»¶зӢ¬з«ӢеҒҮи®ҫгҖӮеңЁ"жңҙзҙ иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁз®—жі•"дёӯпјҢжҲ‘们主иҰҒе…іжіЁд»ҘдёӢеҮ дёӘзҹҘиҜҶзӮ№пјҡ 1. **иҙқеҸ¶ж–Ҝе®ҡзҗҶ**пјҡиҙқеҸ¶ж–Ҝе®ҡзҗҶжҳҜз»ҹи®ЎеӯҰдёӯзҡ„дёҖдёӘйҮҚиҰҒжҰӮеҝөпјҢз”ЁдәҺ...
еңЁжңәеҷЁеӯҰд№ йўҶеҹҹпјҢиҙқеҸ¶ж–ҜеҲҶзұ»жҳҜдёҖз§Қе№ҝжіӣеә”з”Ёзҡ„з»ҹи®Ўж–№жі•пјҢе®ғеҹәдәҺиҙқеҸ¶ж–Ҝе®ҡзҗҶиҝӣиЎҢжҰӮзҺҮйў„жөӢгҖӮеңЁжң¬йЎ№зӣ®дёӯпјҢжҲ‘们关注зҡ„жҳҜдҪҝз”ЁMATLABиҜӯиЁҖе®һзҺ°зҡ„й’ҲеҜ№Irisж•°жҚ®йӣҶзҡ„жңҖе°Ҹй”ҷиҜҜиҙқеҸ¶ж–ҜеҲҶзұ»еҷЁгҖӮMATLABжҳҜе·ҘзЁӢе’Ң科еӯҰи®Ўз®—дёӯеёёз”Ёзҡ„й«ҳзә§...
и®ӯз»ғжӯӨзұ»еҲҶзұ»еҷЁзҡ„з®—жі•дёҚжҳҜеҚ•дёҖзҡ„пјҢиҖҢжҳҜеҹәдәҺе…ұеҗҢеҺҹеҲҷзҡ„дёҖзі»еҲ—з®—жі•пјҡжүҖжңүжңҙзҙ иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁйғҪеҒҮи®ҫзү№е®ҡзү№еҫҒзҡ„еҖјзӢ¬з«ӢдәҺд»»дҪ•е…¶д»–зү№еҫҒзҡ„еҖјпјҢз»ҷе®ҡзұ»еҸҳйҮҸгҖӮдҫӢеҰӮпјҢеҰӮжһңдёҖдёӘж°ҙжһңжҳҜзәўиүІзҡ„гҖҒеңҶеҪўзҡ„гҖҒзӣҙеҫ„зәҰ 10 еҺҳзұіпјҢеҲҷеҸҜд»Ҙи®Өдёәе®ғ...
жңҙзҙ иҙқеҸ¶ж–ҜеҲҶзұ»жҳҜдёҖз§ҚеҹәдәҺжҰӮзҺҮзҡ„жңәеҷЁеӯҰд№ ж–№жі•пјҢе®ғеңЁж•°жҚ®еҲҶзұ»дёӯжңүзқҖе№ҝжіӣзҡ„еә”з”ЁгҖӮиҜҘж–№жі•еҹәдәҺиҙқеҸ¶ж–Ҝе®ҡзҗҶпјҢеҒҮи®ҫзү№еҫҒд№Ӣй—ҙзӣёдә’зӢ¬з«ӢпјҢеӣ жӯӨиў«з§°дёәвҖңжңҙзҙ вҖқгҖӮеңЁиҝҷдёӘе®һдҫӢдёӯпјҢжҲ‘们е°ҶжҺўи®ЁеҰӮдҪ•дҪҝз”Ёжңҙзҙ иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁеӨ„зҗҶIrisж•°жҚ®йӣҶ...
еңЁITйўҶеҹҹпјҢе°Өе…¶жҳҜеңЁж•°жҚ®еҲҶжһҗе’ҢжңәеҷЁеӯҰд№ дёӯпјҢиҙқеҸ¶ж–ҜеҲҶзұ»еҷЁжҳҜдёҖз§Қе№ҝжіӣеә”з”Ёзҡ„з®—жі•гҖӮжң¬ж–Үе°Ҷж·ұе…ҘжҺўи®ЁеҹәдәҺMATLABе®һзҺ°зҡ„иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁеҸҠе…¶еңЁж•°жҚ®еә“еҲҶжһҗдёӯзҡ„еә”з”ЁгҖӮ йҰ–е…ҲпјҢжҲ‘们жқҘзҗҶи§Јд»Җд№ҲжҳҜиҙқеҸ¶ж–ҜеҲҶзұ»еҷЁгҖӮиҙқеҸ¶ж–ҜеҲҶзұ»жҳҜж №жҚ®...
жңҙзҙ иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁжҳҜдёҖз§ҚеҹәдәҺжҰӮзҺҮзҡ„жңәеҷЁеӯҰд№ з®—жі•пјҢе®ғеҹәдәҺиҙқеҸ¶ж–Ҝе®ҡзҗҶе’Ңзү№еҫҒжқЎд»¶зӢ¬з«ӢеҒҮи®ҫгҖӮеңЁеӨ§ж•°жҚ®еӨ„зҗҶйўҶеҹҹпјҢз»“еҗҲHadoopжЎҶжһ¶еҸҜд»Ҙе®һзҺ°еӨ§и§„жЁЎж•°жҚ®йӣҶзҡ„еҲҶзұ»д»»еҠЎгҖӮHadoopжҳҜдёҖдёӘејҖжәҗеҲҶеёғејҸи®Ўз®—жЎҶжһ¶пјҢе®ғе…Ғи®ёеңЁеӨ§йҮҸе»ү价硬件дёҠ...
иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁзҡ„зұ»еһӢжңүеҫҲеӨҡз§ҚпјҢеҢ…жӢ¬жңҙзҙ иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁгҖҒеҚҠжңҙзҙ иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁгҖҒй«ҳж–Ҝжңҙзҙ иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁгҖҒеӨҡйЎ№ејҸжңҙзҙ иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁгҖҒдјҜеҠӘеҲ©жңҙзҙ иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁзӯүгҖӮе…¶дёӯпјҢжңҙзҙ иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁжҳҜжңҖеёёз”Ёзҡ„иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁпјҢе®ғеҒҮи®ҫжүҖжңү...
еңЁиҝҷдёӘвҖңдәәе·ҘжҷәиғҪдёҺжЁЎејҸиҜҶеҲ«дҪңдёҡ2вҖқдёӯпјҢжҲ‘们жҺўи®Ёзҡ„дё»йўҳжҳҜеҰӮдҪ•дҪҝз”ЁиҙқеҸ¶ж–ҜеҲҶзұ»еҷЁжқҘе®һзҺ°дёҖдёӘеҹәдәҺиә«й«ҳзҡ„жҖ§еҲ«еҲҶзұ»зі»з»ҹгҖӮиҙқеҸ¶ж–ҜеҲҶзұ»еҷЁжҳҜдёҖз§ҚеңЁжңәеҷЁеӯҰд№ йўҶеҹҹе№ҝжіӣеә”з”Ёзҡ„жҰӮзҺҮжЁЎеһӢпјҢе°Өе…¶йҖӮеҗҲеӨ„зҗҶе°Ҹ规模数жҚ®йӣҶе’Ңй«ҳз»ҙзү№еҫҒз©әй—ҙзҡ„...
еңЁжң¬йЎ№зӣ®дёӯпјҢжҲ‘们主иҰҒжҺўи®Ёзҡ„жҳҜеҰӮдҪ•еҲ©з”ЁPythonзј–зЁӢиҜӯиЁҖе®һзҺ°дёҖдёӘеҹәдәҺиҙқеҸ¶ж–ҜеҲҶзұ»еҷЁзҡ„еӣҫеғҸеҲҶзұ»зі»з»ҹгҖӮиҝҷдёӘзі»з»ҹзҡ„и®ҫи®ЎжҳҜй’ҲеҜ№жЁЎејҸиҜҶеҲ«иҜҫзЁӢзҡ„дёҖдёӘеӨ§дҪңдёҡпјҢж¶өзӣ–дәҶд»ҺжҺ§еҲ¶еҸ°дәӨдә’еҲ°еӣҫеҪўз”ЁжҲ·з•ҢйқўпјҲGUIпјүзҡ„е…ЁйқўеҠҹиғҪпјҢдҪҝеҫ—з”ЁжҲ·еҸҜд»Ҙ...
иҜҫзЁӢи®ҫи®ЎвҖ”вҖ”еҹәдәҺmatlabзҡ„иҙқеҸ¶ж–ҜеҲҶзұ»еҷЁи®ҫи®ЎпјҢеҢ…еҗ«жңҖе°Ҹй”ҷиҜҜзҺҮиҙқеҸ¶ж–ҜеҲҶзұ»еҷЁгҖҒжңҖе°ҸйЈҺйҷ©иҙқеҸ¶ж–ҜеҶізӯ– д»Јз ҒеҰӮдёӢпјҡ clear; clc; % жҖ»и®ӯз»ғж ·жң¬ж•° N = 29; % зұ»еҲ«ж•°зӣ® w = 4; % жҜҸдёҖдёӘж ·жң¬зҡ„зү№еҫҒж•° n = 3; % и®ӯз»ғж ·жң¬дёӯ...
ж Үйўҳдёӯзҡ„вҖңеҹәдәҺMapReduceзҡ„иҙқеҸ¶ж–ҜеҲҶзұ»вҖқжҢҮзҡ„жҳҜеңЁеӨ§ж•°жҚ®еӨ„зҗҶжЎҶжһ¶HadoopдёҠе®һзҺ°зҡ„иҙқеҸ¶ж–ҜеҲҶзұ»з®—жі•гҖӮиҙқеҸ¶ж–ҜеҲҶзұ»жҳҜдёҖз§Қз»ҹи®ЎеҲҶзұ»жҠҖжңҜпјҢе®ғеҹәдәҺиҙқеҸ¶ж–Ҝе®ҡзҗҶпјҢеёёз”ЁдәҺж–Үжң¬еҲҶзұ»гҖҒеһғеңҫйӮ®д»¶иҝҮж»ӨзӯүйўҶеҹҹгҖӮMapReduceжҳҜGoogleжҸҗеҮәзҡ„дёҖз§Қ...
**Pythonжңҙзҙ иҙқеҸ¶ж–ҜеҲҶзұ»иҜҰи§Ј** жңҙзҙ иҙқеҸ¶ж–ҜеҲҶзұ»пјҲNaive Bayes ClassificationпјүжҳҜдёҖз§ҚеҹәдәҺжҰӮзҺҮзҗҶи®әзҡ„жңәеҷЁеӯҰд№ з®—жі•пјҢе№ҝжіӣеә”з”ЁдәҺж–Үжң¬еҲҶзұ»гҖҒеһғеңҫйӮ®д»¶иҝҮж»ӨгҖҒжғ…ж„ҹеҲҶжһҗзӯүеӨҡдёӘйўҶеҹҹгҖӮеңЁPythonдёӯпјҢжҲ‘们еҸҜд»ҘеҲ©з”Ёscikit-learnеә“...
еңЁжңәеҷЁеӯҰд№ йўҶеҹҹпјҢиҙқеҸ¶ж–ҜеҲҶзұ»еҷЁжҳҜдёҖз§Қе№ҝжіӣеә”з”Ёзҡ„з®—жі•пјҢе°Өе…¶еңЁеӨ„зҗҶж–Үжң¬еҲҶзұ»гҖҒеһғеңҫйӮ®д»¶жЈҖжөӢзӯүй—®йўҳж—¶иЎЁзҺ°еҮәиүІгҖӮеңЁжң¬йЎ№зӣ®дёӯпјҢжҲ‘们е°ҶжҺўи®ЁеҰӮдҪ•еҲ©з”ЁPythonзј–зЁӢиҜӯиЁҖе’Ңз»Ҹе…ёзҡ„Mnistж•°жҚ®йӣҶжқҘе®һзҺ°дёҖдёӘиҙқеҸ¶ж–ҜеҲҶзұ»еҷЁгҖӮMnistж•°жҚ®йӣҶжҳҜ...