- 浏览: 646313 次
- 性别:

- 来自: 武汉
-

文章分类
最新评论
-
lizhuang:
这个方法的内部实现主要是依赖于类加载器,一般的自己实现的类是用 ...
Java中getResourceAsStream的用法 -
prince4426:
回答评论都很精彩
Java中getResourceAsStream的用法 -
kexuetou:
美人如此多娇 写道可能这样总结更好,路径前不带'/',则是相对 ...
Java中getResourceAsStream的用法 -
guoxin91:
...
Java中getResourceAsStream的用法 -
美人如此多娇:
可能这样总结更好,路径前不带'/',则是相对路径;若带,则是绝 ...
Java中getResourceAsStream的用法
Dynamic programming
From Wikipedia, the free encyclopedia
In mathematics and computer science, dynamic programming is a method of solving complex problems by breaking them down into simpler steps. It is applicable to problems that exhibit the properties of overlapping subproblems and optimal substructure (described below). When applicable, the method takes much less time than naive methods.
Bottom-up dynamic programming simply means storing the results of certain calculations, which are then re-used later because the same calculation is a sub-problem in a larger calculation. Bottom-up dynamic programming involves formulating a complex calculation as a recursive series of simpler calculations.
Contents |
History
The term was originally used in the 1940s by Richard Bellman to describe the process of solving problems where one needs to find the best decisions one after another. By 1953, he had refined this to the modern meaning, which refers specifically to nesting smaller decision problems inside larger decisions,and the field was thereafter recognized by the IEEE as a systems analysis and engineering topic. Bellman's contribution is remembered in the name of the Bellman equation, a central result of dynamic programming which restates an optimization problem in recursive form.
Originally the word "programming" in "dynamic programming" had no connection to computer programming, and instead came from the term "mathematical programming"[2] - a synonym for optimization. However, nowadays many optimization problems are best solved by writing a computer program that implements a dynamic programming algorithm, rather than carrying out hundreds of tedious calculations by hand. Some of the examples given below are illustrated using computer programs.
Overview
Dynamic programming is both a mathematical optimization method, and a computer programming method. In both contexts, it refers to simplifying a complicated problem by breaking it down into simpler subproblems in a recursive manner. While some decision problems cannot be taken apart this way, decisions that span several points in time do often break apart recursively; Bellman called this the "Principle of Optimality". Likewise, in computer science, a problem which can be broken down recursively is said to have optimal substructure.
If subproblems can be nested recursively inside larger problems, so that dynamic programming methods are applicable, then there is a relation between the value of the larger problem and the values of the subproblems.[3] In the optimization literature this relationship is called the Bellman equation.
Dynamic programming in mathematical optimization
In terms of mathematical optimization, dynamic programming usually refers to a simplification of a decision by breaking it down into a sequence of decision steps over time. This is done by defining a sequence of value functions V1 , V2 , ... Vn , with an argument y representing the state of the system at times i from 1 to n. The definition of Vn(y) is the value obtained in state y at the last time n. The values Vi at earlier times i=n-1,n-2,...,2,1 can be found by working backwards, using a recursive relationship called the Bellman equation. For i=2,...n, Vi -1 at any state y is calculated from Vi by maximizing a simple function (usually the sum) of the gain from decision i-1 and the function Vi at the new state of the system if this decision is made. Since Vi has already been calculated, for the needed states, the above operation yields Vi -1 for all the needed states. Finally, V1 at the initial state of the system is the value of the optimal solution. The optimal values of the decision variables can be recovered, one by one, by tracking back the calculations already performed.
Dynamic programming in computer programming
As a computer programming method, dynamic programming is mainly used to tackle problems that are solvable in polynomial time.There are two key attributes that a problem must have in order for dynamic programming to be applicable: optimal substructure and overlapping subproblems.
Optimal substructure means that the solution to a given optimization problem can be obtained by the combination of optimal solutions to its subproblems. Consequently, the first step towards devising a dynamic programming solution is to check whether the problem exhibits such optimal substructure. Such optimal substructures are usually described by means of recursion. For example, given a graph G=(V,E), the shortest path p from a vertex u to a vertex v exhibits optimal substructure: take any intermediate vertex w on this shortest path p. If p is truly the shortest path, then the path p1 from u to w and p2 from w to v are indeed the shortest paths between the corresponding vertices (by the simple cut-and-paste argument described in CLRS). Hence, one can easily formulate the solution for finding shortest paths in a recursive manner, which is what the Bellman-Ford algorithm does.
Overlapping subproblems means that the space of subproblems must be small, that is, any recursive algorithm solving the problem should solve the same subproblems over and over, rather than generating new subproblems. For example, consider the recursive formulation for generating the Fibonacci series: Fi = Fi-1 + Fi-2, with base case F1=F2=1. Then F43 = F42 + F41, and F42 = F41 + F40. Now F41 is being solved in the recursive subtrees of both F43 as well as F42. Even though the total number of subproblems is actually small (only 43 of them), we end up solving the same problems over and over if we adopt a naive recursive solution such as this. Dynamic programming takes account of this fact and solves each subproblem only once.

This can be achieved in either of two ways:
- Top-down approach: This is the direct fall-out of the recursive formulation of any problem. If the solution to any problem can be formulated recursively using the solution to its subproblems, and if its subproblems are overlapping, then one can easily memoize or store the solutions to the subproblems in a table. Whenever we attempt to solve a new subproblem, we first check the table to see if it is already solved. If a solution has been recorded, we can use it directly, otherwise we solve the subproblem and add its solution to the table.
- Bottom-up approach: This is the more interesting case. Once we formulate the solution to a problem recursively as in terms of its subproblems, we can try reformulating the problem in a bottom-up fashion: try solving the subproblems first and use their solutions to build-on and arrive at solutions to bigger subproblems. This is also usually done in a tabular form by iteratively generating solutions to bigger and bigger subproblems by using the solutions to small subproblems. For example, if we already know the values of F41 and F40, we can directly calculate the value of F42.
Some programming languages can automatically memoize the result of a function call with a particular set of arguments, in order to speed up call-by-name evaluation (this mechanism is referred to as call-by-need). Some languages make it possible portably (e.g. Scheme, Common Lisp or Perl), some need special extensions (e.g. C++, see [4]). Some languages have automatic memoize built in. In any case, this is only possible for a referentially transparent function.
Example: mathematical optimization
Optimal consumption and saving
A mathematical optimization problem that is often used in teaching dynamic programming to economists (because it can be solved by hand: see Stokey et al., 1989, Chap. 1) concerns a consumer who lives over the periods t = 0,1,2,...,T and must decide how much to consume and how much to save in each period.
Let ct be consumption in period t, and assume consumption yields utility u(ct) = ln(ct) as long as the consumer lives. Assume the consumer is impatient, so that he discounts future utility by a factor b each period, where 0 < b < 1. Let kt be capital in period t. Assume initial capital is a given amount k0 > 0, and suppose that this period's capital and consumption determine next period's capital as 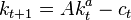 , where A is a positive constant and 0 < a < 1. Assume capital cannot be negative. Then the consumer's decision problem can be written as follows:
, where A is a positive constant and 0 < a < 1. Assume capital cannot be negative. Then the consumer's decision problem can be written as follows:
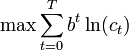 subject to
subject to  for all t = 0,1,2,...,T
for all t = 0,1,2,...,T Written this way, the problem looks complicated, because it involves solving for all the choice variables c0,c1,c2,...,cT and k1,k2,k3,...,kT + 1 simultaneously. (Note that k0 is not a choice variable—the consumer's initial capital is taken as given.)
The dynamic programming approach to solving this problem involves breaking it apart into a sequence of smaller decisions. To do so, we define a sequence of value functions Vt(k), for t = 0,1,2,...,T,T + 1 which represent the value of having any amount of capital k at each time t. Note that VT + 1(k) = 0, that is, there is (by assumption) no utility from having capital after death.
The value of any quantity of capital at any previous time can be calculated by backward induction using the Bellman equation. In this problem, for each t = 0,1,2,...,T, the Bellman equation is
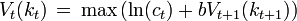 subject to
subject to 
This problem is much simpler than the one we wrote down before, because it involves only two decision variables, ct and kt + 1. Intuitively, instead of choosing his whole lifetime plan at birth, the consumer can take things one step at a time. At time t, his current capital kt is given, and he only needs to choose current consumption ct and saving kt + 1.
To actually solve this problem, we work backwards. For simplicity, the current level of capital is denoted as k. VT + 1(k) is already known, so using the Bellman equation once we can calculate VT(k), and so on until we get to V0(k), which is the value of the initial decision problem for the whole lifetime. In other words, once we know VT − j + 1(k), we can calculate VT − j(k), which is the maximum of ln(cT − j) + bVT − j + 1(Aka − cT − j), where cT − j is the variable and  . It can be shown that the value function at time t = T − j is
. It can be shown that the value function at time t = T − j is
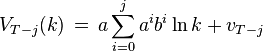
where each vT − j is a constant, and the optimal amount to consume at time t = T − j is
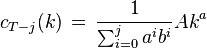
which can be simplified to
 , and
, and 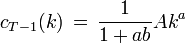 , and
, and 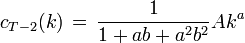 , etcetera.
, etcetera. We see that it is optimal to consume a larger fraction of current wealth as one gets older, finally consuming all current wealth in period T, the last period of life.
[edit] Examples: Computer algorithms
[edit] Fibonacci sequence
Here is a naive implementation of a function finding the nth member of the Fibonacci sequence, based directly on the mathematical definition:
function fib(n)
if n = 0 return 0
if n = 1 return 1
return fib(n − 1) + fib(n − 2)
Notice that if we call, say, fib(5), we produce a call tree that calls the function on the same value many different times:
-
fib(5) -
fib(4) + fib(3) -
(fib(3) + fib(2)) + (fib(2) + fib(1)) -
((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1)) -
(((fib(1) + fib(0)) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
In particular, fib(2) was calculated three times from scratch. In larger examples, many more values of fib, or subproblems, are recalculated, leading to an exponential time algorithm.
Now, suppose we have a simple map object, m, which maps each value of fib that has already been calculated to its result, and we modify our function to use it and update it. The resulting function requires only O(n) time instead of exponential time:
var m := map(0 → 0, 1 → 1)
function fib(n)
if map m does not contain key n
m[n] := fib(n − 1) + fib(n − 2)
return m[n]
This technique of saving values that have already been calculated is called memoization; this is the top-down approach, since we first break the problem into subproblems and then calculate and store values.
In the bottom-up approach we calculate the smaller values of fib first, then build larger values from them. This method also uses O(n) time since it contains a loop that repeats n − 1 times, however it only takes constant (O(1)) space, in contrast to the top-down approach which requires O(n) space to store the map.
function fib(n)
var previousFib := 0, currentFib := 1
if n = 0
return 0
else if n = 1
return 1
repeat n − 1 times
var newFib := previousFib + currentFib
previousFib := currentFib
currentFib := newFib
return currentFib
In both these examples, we only calculate fib(2) one time, and then use it to calculate both fib(4) and fib(3), instead of computing it every time either of them is evaluated.
[edit] A type of balanced 0-1 matrix
Consider the problem of assigning values, either zero or one, to the positions of an n x n matrix, n even, so that each row and each column contains exactly n / 2 zeros and n / 2 ones. For example, when n = 4, three possible solutions are:
+ - - - - + + - - - - + + - - - - + | 0 1 0 1 | | 0 0 1 1 | | 1 1 0 0 | | 1 0 1 0 | and | 0 0 1 1 | and | 0 0 1 1 | | 0 1 0 1 | | 1 1 0 0 | | 1 1 0 0 | | 1 0 1 0 | | 1 1 0 0 | | 0 0 1 1 | + - - - - + + - - - - + + - - - - +
We ask how many different assignments there are for a given n. There are at least three possible approaches: brute force, backtracking, and dynamic programming. Brute force consists of checking all assignments of zeros and ones and counting those that have balanced rows and columns (n / 2 zeros and n / 2 ones). As there are 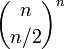 possible assignments, this strategy is not practical except maybe up to n = 6. Backtracking for this problem consists of choosing some order of the matrix elements and recursively placing ones or zeros, while checking that in every row and column the number of elements that have not been assigned plus the number of ones or zeros are both at least n / 2. While more sophisticated than brute force, this approach will visit every solution once, making it impractical for n larger than six, since the number of solutions is already 116963796250 for n = 8, as we shall see. Dynamic programming makes it possible to count the number of solutions without visiting them all.
possible assignments, this strategy is not practical except maybe up to n = 6. Backtracking for this problem consists of choosing some order of the matrix elements and recursively placing ones or zeros, while checking that in every row and column the number of elements that have not been assigned plus the number of ones or zeros are both at least n / 2. While more sophisticated than brute force, this approach will visit every solution once, making it impractical for n larger than six, since the number of solutions is already 116963796250 for n = 8, as we shall see. Dynamic programming makes it possible to count the number of solutions without visiting them all.
We consider  boards, where
boards, where 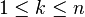 whose k rows contain n / 2 zeros and n / 2 ones. The function f to which memoization is applied maps vectors of n pairs of integers to the number of admissible boards (solutions). There is one pair for each column and its two components indicate respectively the number of ones and zeros that have yet to be placed in that column. We seek the value of
whose k rows contain n / 2 zeros and n / 2 ones. The function f to which memoization is applied maps vectors of n pairs of integers to the number of admissible boards (solutions). There is one pair for each column and its two components indicate respectively the number of ones and zeros that have yet to be placed in that column. We seek the value of 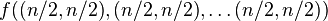 (n arguments or one vector of n elements). The process of subproblem creation involves iterating over every one of
(n arguments or one vector of n elements). The process of subproblem creation involves iterating over every one of  possible assignments for the top row of the board, and going through every column, subtracting one from the appropriate element of the pair for that column, depending on whether the assignment for the top row contained a zero or a one at that position. If any one of the results is negative, then the assignment is invalid and does not contribute to the set of solutions (recursion stops). Otherwise, we have an assignment for the top row of the
possible assignments for the top row of the board, and going through every column, subtracting one from the appropriate element of the pair for that column, depending on whether the assignment for the top row contained a zero or a one at that position. If any one of the results is negative, then the assignment is invalid and does not contribute to the set of solutions (recursion stops). Otherwise, we have an assignment for the top row of the  board and recursively compute the number of solutions to the remaining
board and recursively compute the number of solutions to the remaining 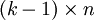 board, adding the numbers of solutions for every admissible assignment of the top row and returning the sum, which is being memoized. The base case is the trivial subproblem, which occurs for a
board, adding the numbers of solutions for every admissible assignment of the top row and returning the sum, which is being memoized. The base case is the trivial subproblem, which occurs for a  board. The number of solutions for this board is either zero or one, depending on whether the vector is a permutation of n / 2 (0,1) and n / 2 (1,0) pairs or not.
board. The number of solutions for this board is either zero or one, depending on whether the vector is a permutation of n / 2 (0,1) and n / 2 (1,0) pairs or not.
For example, in the two boards shown above the sequences of vectors would be
((2, 2) (2, 2) (2, 2) (2, 2)) ((2, 2) (2, 2) (2, 2) (2, 2)) k = 4 0 1 0 1 0 0 1 1 ((1, 2) (2, 1) (1, 2) (2, 1)) ((1, 2) (1, 2) (2, 1) (2, 1)) k = 3 1 0 1 0 0 0 1 1 ((1, 1) (1, 1) (1, 1) (1, 1)) ((0, 2) (0, 2) (2, 0) (2, 0)) k = 2 0 1 0 1 1 1 0 0 ((0, 1) (1, 0) (0, 1) (1, 0)) ((0, 1) (0, 1) (1, 0) (1, 0)) k = 1 1 0 1 0 1 1 0 0 ((0, 0) (0, 0) (0, 0) (0, 0)) ((0, 0) (0, 0), (0, 0) (0, 0))
The number of solutions (sequence A058527 in OEIS) is
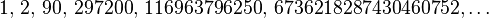
Links to the Perl source of the backtracking approach, as well as a MAPLE and a C implementation of the dynamic programming approach may be found among the external links.
[edit] Checkerboard
Consider a checkerboard with n × n squares and a cost-function c(i, j) which returns a cost associated with square i,j (i being the row, j being the column). For instance (on a 5 × 5 checkerboard),
| 6 | 7 | 4 | 7 | 8 |
| 7 | 6 | 1 | 1 | 4 |
| 3 | 5 | 7 | 8 | 2 |
| - | 6 | 7 | 0 | - |
| - | - | 5* | - | - |
Thus c(1, 3) = 5
Let us say you had a checker that could start at any square on the first rank (i.e., row) and you wanted to know the shortest path (sum of the costs of the visited squares are at a minimum) to get to the last rank, assuming the checker could move only diagonally left forward, diagonally right forward, or straight forward. That is, a checker on (1,3) can move to (2,2), (2,3) or (2,4).
| x | x | x | ||
| o | ||||
This problem exhibits optimal substructure. That is, the solution to the entire problem relies on solutions to subproblems. Let us define a function q(i, j) as
If we can find the values of this function for all the squares at rank n, we pick the minimum and follow that path backwards to get the shortest path.
Note that q(i, j) is equal to the minimum cost to get to any of the three squares below it (since those are the only squares that can reach it) plus c(i, j). For instance:
| A | ||||
| B | C | D | ||

Now, let us define q(i, j) in somewhat more general terms:

The first line of this equation is there to make the recursive property simpler (when dealing with the edges, so we need only one recursion). The second line says what happens in the last rank, to provide a base case. The third line, the recursion, is the important part. It is similar to the A,B,C,D example. From this definition we can make a straightforward recursive code for q(i, j). In the following pseudocode, n is the size of the board, c(i, j) is the cost-function, and min() returns the minimum of a number of values:
function minCost(i, j)
if j < 1 or j > n
return infinity
else if i = 5
return c(i, j)
else
return min( minCost(i+1, j-1), minCost(i+1, j), minCost(i+1, j+1) ) + c(i, j)
It should be noted that this function only computes the path-cost, not the actual path. We will get to the path soon. This, like the Fibonacci-numbers example, is horribly slow since it spends mountains of time recomputing the same shortest paths over and over. However, we can compute it much faster in a bottom-up fashion if we store path-costs in a two-dimensional array q[i, j] rather than using a function. This avoids recomputation; before computing the cost of a path, we check the array q[i, j] to see if the path cost is already there.
We also need to know what the actual shortest path is. To do this, we use another array p[i, j], a predecessor array. This array implicitly stores the path to any square s by storing the previous node on the shortest path to s, i.e. the predecessor. To reconstruct the path, we lookup the predecessor of s, then the predecessor of that square, then the predecessor of that square, and so on, until we reach the starting square. Consider the following code:
function computeShortestPathArrays()
for x from 1 to n
q[1, x] := c(1, x)
for y from 1 to n
q[y, 0] := infinity
q[y, n + 1] := infinity
for y from 2 to n
for x from 1 to n
m := min(q[y-1, x-1], q[y-1, x], q[y-1, x+1])
q[y, x] := m + c(y, x)
if m = q[y-1, x-1]
p[y, x] := -1
else if m = q[y-1, x]
p[y, x] := 0
else
p[y, x] := 1
Now the rest is a simple matter of finding the minimum and printing it.
function computeShortestPath()
computeShortestPathArrays()
minIndex := 1
min := q[n, 1]
for i from 2 to n
if q[n, i] < min
minIndex := i
min := q[n, i]
printPath(n, minIndex)
function printPath(y, x)
print(x)
print("<-")
if y = 2
print(x + p[y, x])
else
printPath(y-1, x + p[y, x])
[edit] Sequence alignment
In genetics, sequence alignment is an important application where dynamic programming is essential [5]. Typically, the problem consists of transforming one sequence into another using edit operations that replace, insert, or remove an element. Each operation has an associated cost, and the goal is to find the sequence of edits with the lowest total cost.
The problem can be stated naturally as a recursion, a sequence A is optimally edited into a sequence B by either:
- inserting the first character of B, and performing an optimal alignment of A and the tail of B
- deleting the first character of A, and performing the optimal alignment of the tail of A and B
- replacing the first character of A with the first character of B, and performing optimal alignments of the tails of A and B.
The partial alignments can be tabulated in a matrix, where cell (i,j) contains the cost of the optimal alignment of A[1..i] to B[1..j]. The cost in cell (i,j) can be calculated by adding the cost of the relevant operations to the cost of its neighboring cells, and selecting the optimum.
Different variants exist, see Smith-Waterman and Needleman-Wunsch.
[edit] Algorithms that use dynamic programming
- Backward induction as a solution method for finite-horizon discrete-time dynamic optimization problems
- Method of undetermined coefficients can be used to solve the Bellman equation in infinite-horizon, discrete-time, discounted, time-invariant dynamic optimization problems
- Many string algorithms including longest common subsequence, longest increasing subsequence, longest common substring, Levenshtein distance (edit distance).
- Many algorithmic problems on graphs can be solved efficiently for graphs of bounded treewidth or bounded clique-width by using dynamic programming on a tree decomposition of the graph.
- The Cocke-Younger-Kasami (CYK) algorithm which determines whether and how a given string can be generated by a given context-free grammar
- The use of transposition tables and refutation tables in computer chess
- The Viterbi algorithm (used for hidden Markov models)
- The Earley algorithm (a type of chart parser)
- The Needleman-Wunsch and other algorithms used in bioinformatics, including sequence alignment, structural alignment, RNA structure prediction.
- Floyd's All-Pairs shortest path algorithm
- Optimizing the order for chain matrix multiplication
- Pseudopolynomial time algorithms for the Subset Sum and Knapsack and Partition problem Problems
- The dynamic time warping algorithm for computing the global distance between two time series
- The Selinger (a.k.a. System R) algorithm for relational database query optimization
- De Boor algorithm for evaluating B-spline curves
- Duckworth-Lewis method for resolving the problem when games of cricket are interrupted
- The Value Iteration method for solving Markov decision processes
- Some graphic image edge following selection methods such as the "magnet" selection tool in Photoshop
- Some methods for solving interval scheduling problems
- Some methods for solving word wrap problems
- Some methods for solving the travelling salesman problem
- Recursive least squares method
- Beat tracking in Music Information Retrieval.
- Adaptive Critic training strategy for artificial neural networks
- Stereo algorithms for solving the Correspondence problem used in stereo vision.
- Seam carving (content aware image resizing)
- The Bellman-Ford algorithm for finding the shortest distance in a graph.
- Some approximate solution methods for the linear search problem.
发表评论
-
《图像超分辨率研究综述》笔记
2010-01-05 09:28 4096图像超分辨率是指由一幅低分辨率图像或图像序列恢复出高分辨率图像 ... -
Jazzy--一种新的拼写检查器API(Java平台)
2010-01-03 22:40 7716计算机擅长执行� ... -
Soundex算法
2010-01-03 19:49 3530Soundex 是一种 20 世纪在美国人口普查中归档姓氏的方 ... -
POJ1191--棋盘分割
2009-12-30 11:09 1540棋盘分割 Time Limit: 1000MS ... -
棋盘覆盖算法
2009-12-29 20:36 3587在一个2^k x 2^k 个方� ... -
贪心算法应用之渴婴问题
2009-12-25 16:31 2309[渴婴问题] 有一个非常渴的、聪明的小婴儿,她可能得到的东西 ... -
十字链表
2009-12-24 16:27 3256十字链表的构成 用链表模拟矩阵的行(或者列,这可以根据个人喜 ... -
常用排序算法实现之冒泡排序(Bubble Sort)
2009-12-19 11:11 1612冒泡排序算法的思想:很简单,每次遍历完序列都把最大(小)的元素 ... -
常用排序算法实现之插入排序(Insertion Sort)
2009-12-19 10:55 1940插入排序(Insertion Sort� ... -
常用排序算法实现之归并排序(Merge Sort)
2009-12-18 18:16 2915归并排序的算法思想是� ... -
完全数
2009-12-17 14:03 2642[定义] 完全数(Perfect number),又称完美数 ... -
Strassen矩阵算法分析及其实现
2009-12-11 15:35 7975对于矩阵乘法 C = A × B,通常的做法是将矩阵进行分 ... -
ACM练习建议(zz)
2009-12-10 21:24 1579一位高手对我的建议:� ... -
ACM算法书籍推荐收藏
2009-12-10 21:06 95581. CLRS 算法导论算法百科全书,只做了前面十几章的习题, ...







相关推荐
代码 随机动态规划的实例的matlab代码代码 随机动态规划的实例的matlab代码代码 随机动态规划的实例的matlab代码代码 随机动态规划的实例的matlab代码代码 随机动态规划的实例的matlab代码代码 随机动态规划的实例的...
动态规划是求解最优化问题的一种方法;动态规划虽然空间复杂度一般较大,但时间效率可观。但是,动态规划在求解中也会存在一些不必要、或者重复求解的子问题,这时就需要进行进一步优化。 在NOI及省选赛场上,一般...
【基于LINGO的优化问题动态规划法求解】 在运筹优化领域,LINGO是一款强大的数学建模软件,尤其适用于解决各种线性、非线性以及动态规划问题。不同于传统方法,LINGO甚至可以在没有明确目标函数的情况下解决动态...
本实验报告主要探讨了使用动态规划算法解决计算二项式系数的问题。实验者刘春云,专业为软件工程,通过这个实验学习并应用了动态规划这一核心的计算机科学概念。实验指导教师为赵晓平,实验时间为2012年2月21日。 *...
动态规划算法经典题目分析 动态规划是一种非常经典的算法思想,解决的问题领域非常广泛。动态规划的基本思想是将一个复杂的问题分解成多个小问题,通过解决这些小问题来解决整个问题。今天,我们将要探讨动态规划的...
动态规划作为解决复杂决策问题的优化技术,被广泛应用于混合动力汽车的能量管理中。 本文介绍的是一套利用MATLAB编写的混合动力汽车能量管理动态规划算法的实现。通过分析提供的代码文件,我们可以对动态规划在混合...
动态规划是信息学竞赛中的常见算法,本文的主要内容就是分析 它的特点。 文章的第一部分首先探究了动态规划的本质,因为动态规划的特 点是由它的本质所决定的。第二部分从动态规划的设计和实现这两个 角度分析了动态...
会议安排(贪心算法和动态规划) 会议安排问题是计算机科学中的一种经典问题,目的是在一系列活动中选择尽可能多的活动,使得每个活动的结束时间不早于下一个活动的开始时间。这个问题可以使用贪心算法和动态规划两...
动态规划是一种重要的算法思想,广泛应用于计算机科学,特别是在解决最优化问题时,如图论、组合优化、机器学习和自然语言处理等领域。在ACM(国际大学生程序设计竞赛)中,动态规划也是常考的题型,因为它能够帮助...
贪心算法、分治算法和动态规划的区别 贪心算法、分治算法和动态规划是三种常用的算法设计策略,每种算法都有其特点和应用场景。下面我们将对这三种算法进行详细的比较和分析。 分治算法 分治算法是一种将原问题...
动态规划是一种解决问题的有效方法,尤其在处理具有重叠子问题和最优子结构的复杂问题时。旅行商问题(Traveling Salesman Problem, TSP)是一个经典的组合优化问题,它的目标是找到一个城市的最短可能路线,使得...
动态规划(Dynamic Programming,简称DP)是一种用于解决最优化问题的算法思想,它通过将大问题分解为相互重叠的子问题,并存储子问题的解,以避免重复计算,从而达到高效求解的目的。DP的核心在于它能够识别并利用...
从给定的文件标题“算法动态规划总结(拓展篇)”和描述“算法动态规划拓展总结,内含详细解说和代码”中,我们可以提炼出一系列关于动态规划算法的知识点,这些知识点涵盖了动态规划的多种应用及其优化技术。...
在现代生产和库存管理中,动态规划作为解决多阶段决策过程优化问题的重要工具,发挥着不可或缺的作用。动态规划的基本思想是将复杂问题分解为相互关联的子问题,并通过求解这些子问题来逐步找到整个问题的最优解。...
"动态规划C语言矩阵连乘" 动态规划是一种非常重要的算法思想,它可以解决很多 Optimization 问题。在这个资源中,我们将学习如何使用动态规划来解决矩阵连乘问题。 动态规划的基本思想是将待解决的问题分解成若干...
标题中的“dynprogs_MATLAB动态规划函数及测试程序_多阶段决策_多阶段规划_together1rz_”表明这是一个关于使用MATLAB实现动态规划算法的资源包,主要用于解决涉及多阶段决策和规划的问题。动态规划是一种在数学、...
动态规划增量动态规划水库优化调度程序代码 动态规划是一种常用的优化算法,它可以解决很多复杂的优化问题。增量动态规划是动态规划的一种变体,它可以更好地解决一些特殊的优化问题。在水库优化调度中,动态规划和...
动态规划解决 TSP 问题 动态规划是一种非常重要的算法思想,在解决复杂问题时非常有用。本次实验主要解决了旅行商问题(TSP),即一个旅行商人要拜访 n 个城市,他必须选择所要走的路径,路径的限制是每个城市只能...
(1) 动态规划算法设计思想。 (2) 金罐游戏问题的动态规划解法。 算法设计与分析-4动态规划金罐游戏.pptx 蛮力法(简单重复递归)和动态规划解决金罐问题 状态数组 子问题 状态方程 蛮力法(时间复杂度O(2n))和...
本篇文章将深入探讨如何运用LINGO来解决动态规划问题,通过具体的案例分析,我们将了解LINGO在动态规划中的应用方法和步骤。 ### 动态规划与LINGO 动态规划是一种用于解决多阶段决策过程中的最优化问题的方法,其...