- 浏览: 203407 次
- 性别:

- 来自: 上海
-

文章分类
最新评论
-
NIghtmare28:
太好用了, 谢谢
Create Local Cloudera Parcels Repo to Save Your ASS -
oyxccyj:
你好,请问下你如上的问题解决了吗?我现在也遇到同样的问题,网上 ...
Homework - HBase Shell, Java Client and MapReduce Job -
20131007:
用java描述算法?
基础数据结构和算法二:Selection sort -
ender35:
第二种实现仅能用于数组排序
计数排序(Counting Sort) -
fy616508150:
我想知道有括号参加运算怎么办
算24算法实现
原文可见:http://www.cnblogs.com/zhangqqqf/archive/2008/09/12/1289730.html
C通过运行时堆栈支持递归函数的实现。递归函数就是直接或间接调用自身的函数。
许多教科书都把计算机阶乘和菲波那契数列用来说明递归,非常不幸我们可爱的著名的老潭老师的《C语言程序设计》一书中就是从阶乘的计算开始的函数递归。导
致读过这本经书的同学们,看到阶乘计算第一个想法就是递归。但是在阶乘的计算里,递归并没有提供任何优越之处。在菲波那契数列中,它的效率更是低的非常恐
怖。
这里有一个简单的程序,可用于说明递归。程序的目的是把一个整数从二进制形式转换为可打印的字符形式。例如:给出一个值4267,我们需要依次产生字符 ‘4’,‘2’,‘6’,和‘7’。就如在printf函数中使用了%d格式码,它就会执行类似处理。
我们采用的策略是把这个值反复除以10,并打印各个余数。例如,4267除10的余数是7,但是我们不能直接打印这个余数。我们需要打印的是机器字符集中 表示数字‘7’的值。在ASCII码中,字符‘7’的值是55,所以我们需要在余数上加上48来获得正确的字符,但是,使用字符常量而不是整型常量可以提 高程序的可移植性。‘0’的ASCII码是48,所以我们用余数加上‘0’,所以有下面的关系:
‘0’+ 0 =‘0’
‘0’+ 1 =‘1’
‘0’+ 2 =‘2’
...
从这些关系中,我们很容易看出在余数上加上‘0’就可以产生对应字符的代码。接着就打印出余数。下一步再取商的值,4267/10等于426。 然后用这个值重复上述步骤。
这种处理方法存在的唯一问题是它产生的数字次序正好相反,它们是逆向打印的。所以在我们的程序中使用递归来修正这个问题。
我们这个程序中的函数是递归性质的,因为它包含了一个对自身的调用。乍一看,函数似乎永远不会终止。当函数调用时,它将调用自身,第2次调用还 将调用自身,以此类推,似乎永远调用下去。这也是我们在刚接触递归时最想不明白的事情。但是,事实上并不会出现这种情况。
这个程序的递归实现了某种类型的螺旋状while循环。while循环在循环体每次执行时必须取得某种进展,逐步迫近循环终止条件。递归函数也 是如此,它在每次递归调用后必须越来越接近某种限制条件。当递归函数符合这个限制条件时,它便不在调用自身 。
在程序中,递归函数的限制条件就是变量quotient为零。在每次递归调用之前,我们都把quotient除以10,所以每递归调用一次,它的值就越来
越接近零。当它最终变成零时,递归便告终止。
/*接受一个整型值(无符号0,把它转换为字符并打印它,前导零被删除*/
#include <stdio.h>
int binary_to_ascii( unsigned int value)
{
unsigned int
quotient;
quotient = value / 10;
if( quotient != 0)
binary_to_ascii( quotient);
putchar ( value % 10 + '0' );
}
递归是如何帮助我们以正确的顺序打印这些字符呢?下面是这个函数的工作流程。
1. 将参数值除以10
2. 如果quotient的值为非零,调用binary-to-ascii打印quotient当前值的各位数字
3. 接着,打印步骤1中除法运算的余数
注意在第2个步骤中,我们需要打印的是quotient当前值的各位数字。我们所面临的问题和最初的问题完全相同,只是变量quotient的 值变小了。我们用刚刚编写的函数(把整数转换为各个数字字符并打印出来)来解决这个问题。由于quotient的值越来越小,所以递归最终会终止。
一旦你理解了递归,阅读递归函数最容易的方法不是纠缠于它的执行过程,而是相信递归函数会顺利完成它的任务。如果你的每个步骤正确无误,你的限 制条件设置正确,并且每次调用之后更接近限制条件,递归函数总是能正确的完成任务。
但是,为了理解递归的工作原理,你需要追踪递归调用的执行过程,所以让我们来进行这项工作。追踪一个递归函数的执行过程的关键是理解函数中所声 明的变量是如何存储的。当函数被调用时,它的变量的空间是创建于运行时堆栈上的。以前调用的函数的变量扔保留在堆栈上,但他们被新函数的变量所掩盖,因此 是不能被访问的。
当递归函数调用自身时,情况于是如此。每进行一次新的调用,都将创建一批变量,他们将掩盖递归函数前一次调用所创建的变量。当我追踪一个递归函 数的执行过程时,必须把分数不同次调用的变量区分开来,以避免混淆。
程序中的函数有两个变量:参数value和局部变量quotient。下面的一些图显示了堆栈的状态,当前可以访问的变量位于栈顶。所有其他调 用的变量饰以灰色的阴影,表示他们不能被当前正在执行的函数访问。
假定我们以4267这个值调用递归函数。当函数刚开始执行时,堆栈的内容如下图所示:

执行除法之后,堆栈的内容如下:

接着,if语句判断出quotient的值非零,所以对该函数执行递归调用。当这个函数第二次被调用之初,堆栈的内容如下:
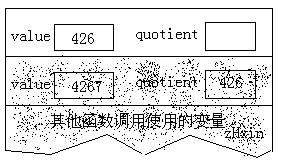
堆栈上创建了一批新的变量,隐藏了前面的那批变量,除非当前这次递归调用返回,否则他们是不能被访问的。再次执行除法运算之后,堆栈的内容如下:

quotient的值现在为42,仍然非零,所以需要继续执行递归调用,并再创建一批变量。在执行完这次调用的出发运算之后,堆栈的内容如下:

此时,quotient的值还是非零,仍然需要执行递归调用。在执行除法运算之后,堆栈的内容如下:
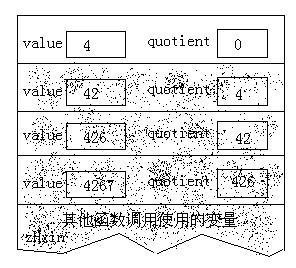
不算递归调用语句本身,到目前为止所执行的语句只是除法运算以及对quotient的值进行测试。由于递归调用这些语句重复执行,所以它的效果 类似循环:当quotient的值非零时,把它的值作为初始值重新开始循环。但是,递归调用将会保存一些信息(这点与循环不同),也就好是保存在堆栈中的 变量值。这些信息很快就会变得非常重要。
现在quotient的值变成了零,递归函数便不再调用自身,而是开始打印输出。然后函数返回,并开始销毁堆栈上的变量值。
每次调用putchar得到变量value的最后一个数字,方法是对value进行模10取余运算,其结果是一个0到9之间的整数。把它与字符常量‘0’ 相加,其结果便是对应于这个数字的ASCII字符,然后把这个字符打印出来。

接着函数返回,它的变量从堆栈中销毁。接着,递归函数的前一次调用重新继续执行,她所使用的是自己的变量,他们现在位于堆栈的顶部。因为它的value值
是42,所以调用putchar后打印出来的数字是2。

接着递归函数的这次调用也返回,它的变量也被销毁,此时位于堆栈顶部的是递归函数再前一次调用的变量。递归调用从这个位置继续执行,这次打印的数字是6。
在这次调用返回之前,堆栈的内容如下:

现在我们已经展开了整个递归过程,并回到该函数最初的调用。这次调用打印出数字7,也就是它的value参数除10的余数。

然后,这个递归函数就彻底返回到其他函数调用它的地点。
如果你把打印出来的字符一个接一个排在一起,出现在打印机或屏幕上,你将看到正确的值:
4267
汉诺塔问题递归算法分析:
一个庙里有三个柱子,第一个有64个盘子,从上往下盘子越来越大。要求庙里的老和尚把这64个盘子全部移动到第三个柱子上。移动的时候始终只能 小盘子压着大盘子。而且每次只能移动一个。
1、此时老和尚(后面我们叫他第一个和尚)觉得很难,所以他想:要是有一个人能把前63个盘子先移动到第二个柱子上,我再把最后一个盘子直接移 动到第三个柱子,再让那个人把刚才的前63个盘子从第二个柱子上移动到第三个柱子上,我的任务就完成了,简单。所以他找了比他年轻的和尚(后面我们叫他第 二个和尚),命令:
① 你丫把前63个盘子移动到第二柱子上
② 然后我自己把第64个盘子移动到第三个柱子上后
③ 你把前63个盘子移动到第三柱子上
2、第二个和尚接了任务,也觉得很难,所以他也和第一个和尚一样想:要是有一个人能把前62个盘子先移动到第三个柱子上,我再把最后一个盘子直接移动到第
二个柱子,再让那个人把刚才的前62个盘子从第三个柱子上移动到第三个柱子上,我的任务就完成了,简单。所以他也找了比他年轻的和尚(后面我们叫他第三和
尚),命令:
① 你把前62个盘子移动到第三柱子上
② 然后我自己把第63个盘子移动到第二个柱子上后
③ 你把前62个盘子移动到第二柱子上
3、第三个和尚接了任务,又把移动前61个盘子的任务依葫芦话瓢的交给了第四个和尚,等等递推下去,直到把任务交给了第64个和尚为止(估计第 64个和尚很郁闷,没机会也命令下别人,因为到他这里盘子已经只有一个了)。
4、到此任务下交完成,到各司其职完成的时候了。完成回推了:
第64个和尚移动第1个盘子,把它移开,然后第63个和尚移动他给自己分配的第2个盘子。
第64个和尚再把第1个盘子移动到第2个盘子上。到这里第64个和尚的任务完成,第63个和尚完成了第62个和尚交给他的任务的第一步。
从上面可以看出,只有第64个和尚的任务完成了,第63个和尚的任务才能完成,只有第2个和尚----第64个和尚的任务完成后,第1个和尚的 任务才能完成。这是一个典型的递归问题。 现在我们以有3个盘子来分析:
第1个和尚命令:
① 第2个和尚你先把第一柱子前2个盘子移动到第二柱子。(借助第三个柱子)
② 第1个和尚我自己把第一柱子最后的盘子移动到第三柱子。
③ 第2个和尚你把前2个盘子从第二柱子移动到第三柱子。
很显然,第二步很容易实现(哎,人总是自私地,把简单留给自己,困难的给别人)。
其中第一步,第2个和尚他有2个盘子,他就命令:
① 第3个和尚你把第一柱子第1个盘子移动到第三柱子。(借助第二柱子)
② 第2个和尚我自己把第一柱子第2个盘子移动到第二柱子上。
③ 第3个和尚你把第1个盘子从第三柱子移动到第二柱子。
同样,第二步很容易实现,但第3个和尚他只需要移动1个盘子,所以他也不用在下派任务了。(注意:这就是停止递归的条件,也叫边界值)
第三步可以分解为,第2个和尚还是有2个盘子,命令:
① 第3个和尚你把第二柱子上的第1个盘子移动到第一柱子。
② 第2个和尚我把第2个盘子从第二柱子移动到第三柱子。
③ 第3个和尚你把第一柱子上的盘子移动到第三柱子。
分析组合起来就是:
1→3 1→2 3→2
借助第三个柱子移动到第二个柱子 |
1→3
自私人留给自己的活|
2→1
2→3 1→3
借助第一个柱子移动到第三个柱子|共需要七步。
如果是4个盘子,则第一个和尚的命令中第1步和第3步各有3个盘子,所以各需要7步,共14步,再加上第1个和尚的1步,所以4个盘子总共需要移动 7+1+7=15步,同样,5个盘子需要15+1+15=31步,6个盘子需要31+1+31=64步……由此可以知道,移动n个盘子需要(2的n次 方)-1步。
从上面整体综合分析可知把n个盘子从1座(相当第一柱子)移到3座(相当第三柱子):
(1)把1座上(n-1)个盘子借助3座移到2座。
(2)把1座上第n个盘子移动3座。
(3)把2座上(n-1)个盘子借助1座移动3座。
下面用hanoi(n,a,b,c)表示把1座n个盘子借助2座移动到3座。
很明显: (1)步上是 hanoi(n-1,1,3,2)
(3)步上是 hanoi(n-1,2,1,3)
用C语言表示出来,就是:
#include <stdio.h>
int method(int n,char a, char b)
{
printf("number..%d..form..%c..to..%c.."n",n,a,b);
return 0;
}
int hanoi(int n,char a,char b,char c)
{
if( n==1 ) move
(1,a,c);
else
{
hanoi(n-1,a,c,b);
move(n,a,c);
hanoi(n-1,b,a,c);
};
return 0;
}
int main()
{
i
nt num;
scanf("%d",&num);
hanoi(num,'A','B','C');
return 0;
}
发表评论
-
基础数据结构和算法十四:Directed Graphs
2013-12-15 22:40 1814In directed graphs, edges a ... -
基础数据结构和算法十三:Undirected Graphs (2)
2013-12-13 22:51 1068Design pattern for graph p ... -
基础数据结构和算法十三:Undirected Graphs
2013-12-13 20:15 1210A graph is a set of vertices ... -
基础数据结构和算法十二:Hash table
2013-12-02 22:06 1058Search algorithms that use ... -
基础数据结构和算法十一:Red-black binary search tree
2013-12-01 12:12 1523The insertion algorithm fo ... -
基础数据结构和算法十:2-3 search tree
2013-11-30 11:07 1225Binary search tree works w ... -
基础数据结构和算法九:Binary Search Tree
2013-11-28 22:39 1682A binary search tree (BST) ... -
基础数据结构和算法八:Binary search
2013-11-28 21:21 1158Binary search needs an ordere ... -
基础数据结构和算法七:Priority queue & Heap sort
2013-11-27 19:47 2720Some important applications o ... -
基础算法七: Priority queue & Heap sort
2013-11-26 21:46 0Some important applications ... -
基础数据结构和算法六:Quick sort
2013-11-21 19:33 1246Quick sort is probably used m ... -
Inversions of an array
2013-11-20 22:28 0TODO -
基础数据结构和算法五:Merge sort
2013-11-20 21:44 2000One of mergesort’s most at ... -
基础数据结构和算法四:Shell sort
2013-11-20 19:11 1195Shellsort is a simple exte ... -
Comparing two sorting algorithms
2013-11-19 21:16 869Generally we compare algorith ... -
基础数据结构和算法三:Insertion Sort
2013-11-19 21:06 1010As in selection sort, the ite ... -
基础数据结构和算法二:Selection sort
2013-11-19 20:57 1185One of the simplest sortin ... -
基础数据结构和算法一:UnionFind
2013-11-19 20:47 1288The problem that we consid ... -
Three-sum with linear time complexity
2013-09-14 10:08 0TODO package org.george.algor ... -
Blooming Filter in Hadoop
2013-07-27 22:49 0TODO





相关推荐
递归算法是一种在软件开发中常用的技术,其核心在于函数直接或间接地调用自身来解决问题。递归算法的实现依赖于运行时堆栈,每次函数调用都会在堆栈上分配空间来保存局部变量和返回地址。在这个过程中,每次递归调用...
递归算法是一种重要的程序设计思想,它在解决数学问题和计算机科学中有着广泛的应用。递归算法的原理是将一个大问题分解成小问题,通过解决小问题来解决大问题,这种方法与数学归纳法有异曲同工之妙。在计算机科学中...
在编程领域,递归算法是一种强大的工具,尤其在数据结构的处理中发挥着重要作用。递归算法基于函数自我调用的原理,通过不断分解问题来达到解决问题的目的。它能够简化复杂问题的解决逻辑,但同时也可能带来性能上的...
递归算法是一种强大的编程技术,它基于函数或过程在解决问题时自我引用的特性。通过将大问题分解为规模更小的相同或相似子问题来解决,递归算法常常用于简化复杂的计算任务。以下是对递归算法的详细解释: 1. **...
本文将深入探讨递归的各个方面,帮助读者从基础到高级逐步掌握递归算法。 首先,理解什么是递归至关重要。递归发生在一个函数内部调用自身的情况。以阶乘函数为例,函数`f(n)`通过调用`f(n - 1)`来计算`n`的阶乘,...
递归算法是一种编程技术,它涉及程序调用自身以解决问题。这种技术的核心在于递归方程和递归终止条件。递归方程是描述问题或算法如何通过自我调用来逐步解决的公式,而终止条件则是防止无限循环并确保算法最终能够...
汉诺塔问题是一个经典的递归算法问题,它源自印度的一个古老传说,旨在通过演示如何将一组盘子从一根柱子移动到另一根柱子来解释宇宙的起源。在这个问题中,我们有三根柱子A、B和C,以及N个大小不一的盘子,初始时...
### 中序遍历二叉树非递归算法详解 #### 1. 理解中序遍历的基本概念 中序遍历是一种按照左子树、根节点、右子树的顺序访问二叉树所有节点的过程。对于每个节点,先遍历其左子树,然后访问该节点本身,最后遍历其右...
【C#递归算法详解】 递归算法是编程中一种重要的技术,特别是在C#这样的面向对象语言中。它涉及到函数自身调用自身的过程,通过解决更小规模的问题来解决整个问题。递归算法的核心概念包括两个关键部分:基础情况...
递归算法是一种强大的编程技术,它通过函数或过程在解决问题时调用自身来解决更小规模的相同问题。递归的基本概念在于一个函数在定义中包含对自身的引用,或者问题的解决方案依赖于较小规模问题的解决方案。在程序...
Java递归算法是一种重要的编程技巧,它通过函数或方法直接或间接地调用自身来解决问题。在Java中,递归通常用于简化复杂的问题,并且在数据结构(如树和图的遍历)、数学计算(如斐波纳契数列)等领域有着广泛应用。...
Python装饰器与递归算法详解 Python是一种极其灵活和强大的编程语言,它提供了多种高级编程技巧来提升代码的复用性、可读性和维护性。在这些技巧中,装饰器和递归算法是最具特色的两种。本文将深入探讨这两者的概念...
**Python 递归算法详解** 递归算法是编程领域中的一种基本策略,它涉及函数或过程的自我调用。在Python中,递归是通过定义一个可以调用自身的函数来实现的。递归算法的核心思想是将复杂问题分解成较小的子问题,...
### 递归算法专题知识点详解 #### 一、递归算法原理 递归算法是一种将问题分解成子问题的方法,其中子问题与原问题性质相同但规模较小。递归算法的关键在于识别出能够通过递归解决的问题,并找到递归的基本情况...
递归算法详解 递归算法是ACM基础算法之一,通过运行时堆栈支持递归函数的实现。递归函数就是直接或间接调用自身的函数。许多教科书都把计算机阶乘和菲波那契数列用来说明递归,但是这些例子并没有提供任何优越之处...
### C语言中的递归算法详解 #### 一、递归的基本概念 递归是一种重要的算法设计技巧,它指的是函数直接或间接地调用自身的过程。递归算法在解决某些问题时能够提供简洁高效的解决方案,尤其是在处理具有自然递归...
### 知识点详解:简单的递归算法与斐波那契数列 #### 一、递归算法概览 递归算法是一种通过调用自身来解决问题的方法,它将复杂问题分解为更小的子问题,直到子问题简单到可以直接求解为止。递归算法的关键在于...
### 三维地形绘制——四叉树递归算法详解 #### 一、引言 三维地形绘制是GIS领域中一个非常重要的技术,它涉及到如何高效、真实地表示地球表面的复杂地形。在三维地形渲染中,一种常用的技术是利用LOD(Level of ...