数学符号

mousetwo

浏览: 3208 次
性别:
来自: 重庆

最近访客更多访客>>

woodding2008

博主相关

博客

微博

相册

留言

关于我

文章分类

全部博客 (3)

社区版块

存档分类

數學上，有一組常在數學表達式中出現的符號。數學工作者熟悉這些符號，不是每次使用都加以說明。所以，對於數學初學者，下面的列表給出了很多常見的符號包括名稱、讀法和應用領域。另外，第三欄有一個非正式的定義，第四欄有個簡單的例子。

注意，有時候不同符號有相同含義，而有些符號在不同的上下文中有不同的含義。

符號

名稱定義舉例讀法數學領域

=	等號	x = y 表示 x 和 y 是相同的東西或其值相等。	1 + 1 = 2
等於
所有領域
≠	不等號	x ≠ y 表示 x 和 y 不是相同的東西或其值不相等。	1 ≠ 2
不等於
所有領域
< >	嚴格不等號	x < y 表示 x 小於y 。 x > y 表示 x 大於y 。	3 < 4 5 > 4
小於，大於
序理論
≤ ≥	不等號	x ≤ y 表示 x 小於或等於y 。 x ≥ y 表示 x 大於或等於y 。	3 ≤ 4；5 ≤ 5 5 ≥ 4；5 ≥ 5
小於等於，大於等於
序理論
+	加號	4 + 6 表示 4 加 6。	2 + 7 = 9
加
算術
−	減號	9 − 4 表示 9 減 4。	8 − 3 = 5
減
算術
負號	− 3 表示 3 的負數。	− (− 5) = 5
負
算術
補集	A − B 表示包含所有屬於 A 但不屬於 B 的元素的集合。	{1,2,4} − {1,3,4} = {2}
減
集合論
×	乘號	3 × 4 表示 3 乘以 4。	7 × 8 = 56
乘以
算術
直積	X × Y 表示所有第一個元素屬於 X ，第二個元素屬於 Y 的有序對的集合。	{1,2} × {3,4} = {(1,3),(1,4),(2,3),(2,4)}
… 和…的直積
集合論
向量積	u × v 表示向量 u 和 v 的向量積。	(1,2,5) × (3,4,− 1) = (− 22, 16, − 2)
向量積
向量代數
÷ /	除號	6 ÷ 3 或 6 / 3 表示 6 除以 3。	2 ÷ 4 = 0.5 12/4 = 3
除以
算術
√	根號	√ x 表示其平方為 x 的正數与负數。	√ 4 = ±2
…的平方根
實數
復根號	若用極坐標表示複數 z = r exp(i φ )（滿足 -π < φ ≤ π ），則 √ z = √ r exp(i φ /2)。	√ (-1) = i
…的平方根
複數
\| \|	絕對值	\|x \| 表示實數軸（或復平面）上 x 和 0 的距離。	\|3\| = 3, \|-5\| = \|5\| \|i \| = 1, \|3+4i \| = 5
…的絕對值
數
!	階乘	n ! 表示連乘積 1× 2× …× n 。	4! = 1 × 2 × 3 × 4 = 24
…的階乘
組合論
~	概率分佈	X ~ D 表示隨機變量 X 概率分佈為 D 。	X ~ N(0,1) ：標準正態分佈
滿足分佈
統計學
⇒ → ⊃	實質蘊涵	A ⇒ B 表示 A 真則 B 也真；A 假則 B 不定。 → 可能和 ⇒ 一樣，或者有下面將提到的函數的意思。 ⊃ 可能和 ⇒ 一樣，或者有下面將提到的父集的意思。	x = 2 ⇒ x ² = 4 為真，但 x ² = 4 ⇒ x = 2 一般情況下為假（因為 x 可以是 − 2）。
推出，若…則 …
命題邏輯
⇔ ↔	實質等價	A ⇔ B 表示 A 真則 B 真，A 假則 B 假。	x + 5 = y +2 ⇔ x + 3 = y
當且僅當
命題邏輯
¬ ˜	邏輯非	命題 ¬ A 為真當且僅當 A 為假。將一條斜線穿過一個符號相當於將 "¬ " 放在該符號前面。	¬ (¬ A ) ⇔ A x ≠ y ⇔ ¬ (x = y )
非，不
命題邏輯
∧	邏輯與或交運算	若 A 為真且 B 為真，則命題 A ∧ B 為真；否則為假。	n < 4 ∧ n >2 ⇔ n = 3，當 n 是自然數
與
命題邏輯，格理論
∨	邏輯或或並運算	若 A 或 B （或都）為真，則命題 A ∨ B 為真；若兩者都假則命題為假。	n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3，當 n 是自然數
或
命題邏輯，格理論
⊕ ⊻	異或	若 A 和 B 剛好有一個為真，則命題 A ⊕ B 為真。 A ⊻ B 的意義相同。	(¬ A ) ⊕ A 恆為真，A ⊕ A 恆為假。
異或
命題邏輯，布爾代數
∀	全稱量詞	∀ x : P (x ) 表示 P (x ) 對於所有 x 為真。	∀ n ∈ N : n ² ≥ n
對所有；對任意；對任一
謂詞邏輯
∃	存在量詞	∃ x : P (x ) 表示存在至少一個 x 使得 P (x ) 為真。	∃ n ∈ N : n 為偶數
存在
謂詞邏輯
∃ !	唯一量詞	∃ ! x : P (x ) 表示有且僅有一個 x 使得 P (x ) 為真。	∃ ! n ∈ N : n + 5 = 2n
存在唯一
謂詞邏輯
:= ≡ :⇔	定義	x := y 或 x ≡ y 表示 x 定義為 y 的一個名字（注意：≡ 也可表示其它意思，例如全等）。 P :⇔ Q 表示 P 定義為 Q 的邏輯等價。	cosh x := (1/2)(exp x + exp (− x )) A XOR B :⇔ (A ∨ B ) ∧ ¬ (A ∧ B )
定義為
所有領域
{ , }	集合括號	{a ,b ,c } 表示 a , b ,c 組成的集合。	N = {0,1,2,…}
…的集合
集合論
{ : } { \| }	集合構造記號	{x : P (x )} 表示所有滿足 P (x ) 的 x 的集合。 {x \| P (x )} 和 {x : P (x )} 的意義相同。	{n ∈ N : n ² < 20} = {0,1,2,3,4}
滿足…的集合
集合論
∅ {}	空集	∅ 表示沒有元素的集合。 {} 的意義相同。	{n ∈ N : 1 < n ² < 4} = ∅
空集
集合論
∈ ∉	元素歸屬性質	a ∈ S 表示 a 屬於集合 S ；a ∉ S 表示 a 不屬於 S 。	(1/2)^− 1 ∈ N 2^− 1 ∉ N
屬於；不屬於
所有領域
⊆ ⊂	子集	A ⊆ B 表示 A 的所有元素屬於 B 。 A ⊂ B 表示 A ⊆ B 但 A ≠ B 。	A ∩ B ⊆ A ；Q ⊂ R
…的子集
集合論
⊇ ⊃	父集	A ⊇ B 表示 B 的所有元素屬於 A 。 A ⊃ B 表示 A ⊇ B 但 A ≠ B 。	A ∪ B ⊇ B ；R ⊃ Q
…的父集
集合論
∪	並集	A ∪ B 表示包含所有 A 和 B 的元素但不包含任何其他元素的集合。	A ⊆ B ⇔ A ∪ B = B
…和…的並集
集合論
∩	交集	A ∩ B 表示包含所有同時屬於 A 和 B 的元素的集合。	{x ∈ R : x ² = 1} ∩ N = {1}
…和…的交集
集合論
\	補集	A \ B 表示所有屬於 A 但不屬於 B 的元素的集合。	{1,2,3,4} \ {3,4,5,6} = {1,2}
減；除去
集合論
( )	函數應用	f (x ) 表示 f 在 x 的值。	f (x ) := x ² ，則 f (3) = 3² = 9。
f (x )
集合論
優先組合	先執行括號內的運算。	(8/4)/2 = 2/2 = 1；8/(4/2) = 8/2 = 4

所有領域
ƒ :X → Y	函數箭頭	ƒ : X → Y 表示 ƒ 從集合 X 映射到集合 Y 。	設ƒ : Z → N 定義為 ƒ (x ) = x ² 。
從…到…
集合論
o	復合函數	f o g 是一個函數，使得 (f o g )(x ) = f (g (x ))。	若 f (x ) = 2x ，且 g (x ) = x + 3，則 (f o g )(x ) = 2(x + 3)。
復合
集合論
N ℕ	自然數	N 表示 {1,2,3,…}，另一定義參見自然數條目。	{\|a \| : a ∈ Z } = N
N
數
Z ℤ	整數	Z 表示 {…,− 3,− 2,− 1,0,1,2,3,…}。	{a : \|a \| ∈ N } = Z
Z
數
Q ℚ	有理數	Q 表示 {p /q : p ,q ∈ Z , q ≠ 0}。	3.14 ∈ Q π ∉ Q
Q
數
R ℝ	實數	R 表示 {lim_n→ ∞ a _n : ∀ n ∈ N : a _n ∈ Q , 極限存在}。	π ∈ R √ (− 1) ∉ R
R
數
C ℂ	複數	C 表示 {a + bi : a ,b ∈ R }。	i = √ (− 1) ∈ C
C
數
∞	無窮	∞ 是擴展的實數軸上大於任何實數的數；通常出現在極限中。	lim_x→ 0 1/\|x \| = ∞
無窮
數
π	圓周率	π 表示圓周長和直徑之比。	A = π r ² 是半徑為 r 的圓的面積
pi
幾何
\|\| \|\|	范數	\|\|x \|\| 是賦范線性空間元素 x 的范數。	\|\|x +y \|\| ≤ \|\|x \|\| + \|\|y \|\|
…的范數；…的長度
線性代數
∑	求和	∑ _k =1ⁿ a _k 表示 a ₁ + a ₂ + … + a _n .	∑ _k =1⁴ k ² = 1² + 2² + 3² + 4² = 1 + 4 + 9 + 16 = 30
從…到…的和
算術
∏	求積	∏ _k =1ⁿ a _k 表示 a ₁a ₂· · · a _n .	∏ _k =1⁴ (k + 2) = (1 + 2)(2 + 2)(3 + 2)(4 + 2) = 3 × 4 × 5 × 6 = 360
從…到…的積
算術
直積	∏ _i =0ⁿY _i 表示所有 (n+1)-元組 (y ₀ ,…,y _n )。	∏ _n =1³R = R ⁿ
…的直積
集合論
'	導數	f '(x )函數f 在x 點的倒數，也就是，那裡的切線斜率。	若 f (x ) = x ² , 則 f '(x ) = 2x
… 撇; …的導數
微積分
∫	不定積分或反導數	∫ f (x ) dx 表示導數為f 的函數.	∫ x ² dx = x ³ /3
…的不定積分; …的反導數
微積分
定積分	∫ _a^b f (x ) dx 表示 x -軸和 f 在 x = a 和x = b 之間的函數圖像所夾成的帶符號面積。	∫ ₀^b x² dx = b ³ /3;
從…到…以…為變量的積分
微積分
∇	梯度	∇ f (x₁ , … , x_n ) 偏導數組成的向量 (df / dx ₁ , … , df / dx _n ).	若 f (x ,y ,z ) = 3xy + z ² 則 ∇ f = (3y , 3x , 2z )
…的(del 或nabla 或梯度 )
微積分
∂	偏導數	設有f (x₁ , … , x_n ), ∂ f/∂ x_i 是f 的對於x_i 的當其他變量保持不變時的導數.	若 f (x,y) = x² y, 則 ∂ f /∂ x = 2xy
…的偏導數
微積分
邊界	∂ M 表示M 的邊界	∂ {x : \|\|x\|\| ≤ 2} = {x : \|\| x \|\| = 2}
…的邊界
拓撲
次數	∂ f(x) 表示f(x) 的次數( 也記作degf(x) )
…的次數
多項式
⊥	垂直	x ⊥ y 表示 x 垂直於y ; 更一般的 x 正交於y .	若 l ⊥ m 和m ⊥ n 則 l \|\| n .
垂直於
幾何
底元素	x = ⊥ 表示 x 是最小的元素.	∀ x : x ∧ ⊥ = ⊥
底元素
格理論
⊧	蘊含	A ⊧ B 表示A 蘊含B , 在A 成立的每個模型中， B 也成立.	A ⊧ A ∨ ¬ A
蘊含；
模型論
⊢	推導	x ⊢ y 表示 y 由 x 導出.	A → B ⊢ ¬ B → ¬ A
從…導出
命題邏輯 , 謂詞邏輯
◅	正則子群	N ◅ G 表示 N 是G 的正則子群.	Z (G ) ◅ G
是…的正則子群
群論
/	商群	G /H 表示G 模其子群H 的商群.	{0, a , 2a , b , b +a , b +2a } / {0, b } = {{0, b }, {a , b +a }, {2a , b +2a }}
模
群論
≈	同構	G ≈ H 表示 G 同構於 H	Q / {1, − 1} ≈ V , 其中 Q 是四元數群 V 是克萊因四群 .
同構於
群論
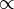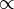$\propto$	正比	G $\propto$ H 表示 G 正比於 H	若Q 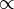$\propto$ V ，则 Q =KV
正比於
所有领域