ж‘ҳеҪ•иҮӘпјҡ
http://www.blogjava.net/zhenandaci/archive/2009/02/13/254578.html
дёҠиҠӮиҜҙеҲ°жҲ‘们жңүдәҶдёҖдёӘзәҝжҖ§еҲҶзұ»еҮҪж•°пјҢд№ҹжңүдәҶеҲӨж–ӯи§ЈдјҳеҠЈзҡ„ж ҮеҮҶвҖ”вҖ”еҚіжңүдәҶдјҳеҢ–зҡ„зӣ®ж ҮпјҢиҝҷдёӘзӣ®ж Үе°ұжҳҜжңҖеӨ§еҢ–еҮ дҪ•й—ҙйҡ”пјҢдҪҶжҳҜзңӢиҝҮдёҖдәӣе…ідәҺSVMзҡ„и®әж–Үзҡ„дәәдёҖе®ҡи®°еҫ—д»Җд№ҲдјҳеҢ–зҡ„зӣ®ж ҮжҳҜиҰҒжңҖе°ҸеҢ–||w||иҝҷж ·зҡ„иҜҙжі•пјҢиҝҷжҳҜжҖҺд№ҲеӣһдәӢе‘ўпјҹеӣһеӨҙеҶҚзңӢзңӢжҲ‘们еҜ№й—ҙйҡ”е’ҢеҮ дҪ•й—ҙйҡ”зҡ„е®ҡд№үпјҡ
й—ҙйҡ”пјҡОҙ=y(wx+b)=|g(x)|
еҮ дҪ•й—ҙйҡ”пјҡ

еҸҜд»ҘзңӢеҮәОҙ=||w||ОҙеҮ дҪ•гҖӮжіЁж„ҸеҲ°еҮ дҪ•й—ҙйҡ”дёҺ||w||жҳҜжҲҗеҸҚжҜ”зҡ„пјҢеӣ жӯӨжңҖеӨ§еҢ–еҮ дҪ•й—ҙйҡ”дёҺжңҖе°ҸеҢ–||w||е®Ңе…ЁжҳҜдёҖеӣһдәӢгҖӮиҖҢжҲ‘们常用зҡ„方法并дёҚжҳҜеӣәе®ҡ||w||зҡ„еӨ§е°ҸиҖҢеҜ»жұӮжңҖеӨ§еҮ дҪ•й—ҙйҡ”пјҢиҖҢжҳҜеӣәе®ҡй—ҙйҡ”пјҲдҫӢеҰӮеӣәе®ҡдёә1пјүпјҢеҜ»жүҫжңҖе°Ҹзҡ„||w||гҖӮ
иҖҢеҮЎжҳҜжұӮдёҖдёӘеҮҪж•°зҡ„жңҖе°ҸеҖјпјҲжҲ–жңҖеӨ§еҖјпјүзҡ„й—®йўҳйғҪеҸҜд»Ҙз§°дёәеҜ»дјҳй—®йўҳпјҲд№ҹеҸ«дҪңдёҖдёӘ规еҲ’й—®йўҳпјүпјҢеҸҲз”ұдәҺжүҫжңҖеӨ§еҖјзҡ„й—®йўҳжҖ»еҸҜд»ҘйҖҡиҝҮеҠ дёҖдёӘиҙҹеҸ·еҸҳдёәжүҫжңҖе°ҸеҖјзҡ„й—®йўҳпјҢеӣ жӯӨжҲ‘们дёӢйқўи®Ёи®әзҡ„ж—¶еҖҷйғҪй’ҲеҜ№жүҫжңҖе°ҸеҖјзҡ„иҝҮзЁӢжқҘиҝӣиЎҢгҖӮдёҖдёӘеҜ»дјҳй—®йўҳжңҖйҮҚиҰҒзҡ„йғЁеҲҶжҳҜзӣ®ж ҮеҮҪж•°пјҢйЎҫеҗҚжҖқд№үпјҢе°ұжҳҜжҢҮеҜ»дјҳзҡ„зӣ®ж ҮгҖӮдҫӢеҰӮжҲ‘们жғіеҜ»жүҫжңҖе°Ҹзҡ„||w||иҝҷ件дәӢпјҢе°ұеҸҜд»Ҙз”ЁдёӢйқўзҡ„ејҸеӯҗиЎЁзӨәпјҡ
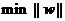
дҪҶе®һйҷ…дёҠеҜ№дәҺиҝҷдёӘзӣ®ж ҮпјҢжҲ‘们常常дҪҝз”ЁеҸҰдёҖдёӘе®Ңе…Ёзӯүд»·зҡ„зӣ®ж ҮеҮҪж•°жқҘд»ЈжӣҝпјҢйӮЈе°ұжҳҜпјҡ
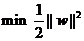
(ејҸ1)
дёҚйҡҫзңӢеҮәеҪ“||w||2иҫҫеҲ°жңҖе°Ҹж—¶пјҢ||w||д№ҹиҫҫеҲ°жңҖе°ҸпјҢеҸҚд№ӢдәҰ然пјҲеүҚжҸҗеҪ“然жҳҜ||w||жҸҸиҝ°зҡ„жҳҜеҗ‘йҮҸзҡ„й•ҝеәҰпјҢеӣ иҖҢжҳҜйқһиҙҹзҡ„пјүгҖӮд№ӢжүҖд»ҘйҮҮз”Ёиҝҷз§ҚеҪўејҸпјҢжҳҜеӣ дёәеҗҺйқўзҡ„жұӮи§ЈиҝҮзЁӢдјҡеҜ№зӣ®ж ҮеҮҪж•°дҪңдёҖзі»еҲ—еҸҳжҚўпјҢиҖҢејҸпјҲ1пјүзҡ„еҪўејҸдјҡдҪҝеҸҳжҚўеҗҺзҡ„еҪўејҸжӣҙдёәз®ҖжҙҒпјҲжӯЈеҰӮиҒӘжҳҺзҡ„иҜ»иҖ…жүҖж–ҷпјҢж·»еҠ зҡ„зі»ж•°дәҢеҲҶд№ӢдёҖе’Ңе№іж–№пјҢзҡҶжҳҜдёәжұӮеҜјж•°жүҖйңҖпјүгҖӮ
жҺҘдёӢжқҘжҲ‘们иҮӘ然дјҡй—®зҡ„е°ұжҳҜпјҢиҝҷдёӘејҸеӯҗжҳҜеҗҰе°ұжҸҸиҝ°дәҶжҲ‘们зҡ„й—®йўҳе‘ўпјҹпјҲеӣһжғідёҖдёӢпјҢжҲ‘们зҡ„й—®йўҳжҳҜжңүдёҖе ҶзӮ№пјҢеҸҜд»Ҙиў«еҲҶжҲҗдёӨзұ»пјҢжҲ‘们иҰҒжүҫеҮәжңҖеҘҪзҡ„еҲҶзұ»йқўпјү
еҰӮжһңзӣҙжҺҘжқҘи§ЈиҝҷдёӘжұӮжңҖе°ҸеҖјй—®йўҳпјҢеҫҲе®№жҳ“зңӢеҮәеҪ“||w||=0зҡ„ж—¶еҖҷе°ұеҫ—еҲ°дәҶзӣ®ж ҮеҮҪж•°зҡ„жңҖе°ҸеҖјгҖӮдҪҶжҳҜдҪ д№ҹдјҡеҸ‘зҺ°пјҢж— и®әдҪ з»ҷд»Җд№Ҳж ·зҡ„ж•°жҚ®пјҢйғҪжҳҜиҝҷдёӘи§ЈпјҒеҸҚжҳ еңЁеӣҫдёӯпјҢе°ұжҳҜH1дёҺH2дёӨжқЎзӣҙзәҝй—ҙзҡ„и·қзҰ»ж— йҷҗеӨ§пјҢиҝҷдёӘж—¶еҖҷпјҢжүҖжңүзҡ„ж ·жң¬зӮ№пјҲж— и®әжӯЈж ·жң¬иҝҳжҳҜиҙҹж ·жң¬пјүйғҪи·‘еҲ°дәҶH1е’ҢH2дёӯй—ҙпјҢиҖҢжҲ‘们еҺҹжң¬зҡ„ж„ҸеӣҫжҳҜпјҢH1еҸідҫ§зҡ„иў«еҲҶдёәжӯЈзұ»пјҢH2 е·Ұдҫ§зҡ„иў«еҲҶдёәиҙҹзұ»пјҢдҪҚдәҺдёӨзұ»дёӯй—ҙзҡ„ж ·жң¬еҲҷжӢ’з»қеҲҶзұ»пјҲжӢ’з»қеҲҶзұ»зҡ„еҸҰдёҖз§ҚзҗҶи§ЈжҳҜеҲҶз»ҷе“ӘдёҖзұ»йғҪжңүйҒ“зҗҶпјҢеӣ иҖҢеҲҶз»ҷе“ӘдёҖзұ»д№ҹйғҪжІЎжңүйҒ“зҗҶпјүгҖӮиҝҷдёӢеҸҜеҘҪпјҢжүҖжңүж ·жң¬зӮ№йғҪиҝӣе…ҘдәҶж— жі•еҲҶзұ»зҡ„зҒ°иүІең°еёҰгҖӮ
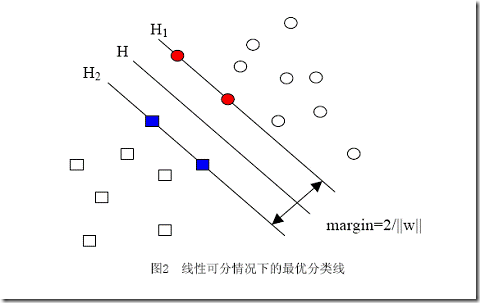
йҖ жҲҗиҝҷз§Қз»“жһңзҡ„еҺҹеӣ жҳҜеңЁжҸҸиҝ°й—®йўҳзҡ„ж—¶еҖҷеҸӘиҖғиҷ‘дәҶзӣ®ж ҮпјҢиҖҢжІЎжңүеҠ е…ҘзәҰжқҹжқЎд»¶пјҢзәҰжқҹжқЎд»¶е°ұжҳҜеңЁжұӮи§ЈиҝҮзЁӢдёӯеҝ…йЎ»ж»Ўи¶ізҡ„жқЎд»¶пјҢдҪ“зҺ°еңЁжҲ‘们зҡ„й—®йўҳдёӯе°ұжҳҜж ·жң¬зӮ№еҝ…йЎ»еңЁH1жҲ–H2зҡ„жҹҗдёҖдҫ§пјҲжҲ–иҖ…иҮіе°‘еңЁH1е’ҢH2дёҠпјүпјҢиҖҢдёҚиғҪи·‘еҲ°дёӨиҖ…дёӯй—ҙгҖӮжҲ‘们еүҚж–ҮжҸҗеҲ°иҝҮжҠҠй—ҙйҡ”еӣәе®ҡдёә1пјҢиҝҷжҳҜжҢҮжҠҠжүҖжңүж ·жң¬зӮ№дёӯй—ҙйҡ”жңҖе°Ҹзҡ„йӮЈдёҖзӮ№зҡ„й—ҙйҡ”е®ҡдёә1пјҲиҝҷд№ҹжҳҜйӣҶеҗҲзҡ„й—ҙйҡ”зҡ„е®ҡд№үпјҢжңүзӮ№з»•еҳҙпјүпјҢд№ҹе°ұж„Ҹе‘ізқҖйӣҶеҗҲдёӯзҡ„е…¶д»–зӮ№й—ҙйҡ”йғҪдёҚдјҡе°ҸдәҺ1пјҢжҢүз…§й—ҙйҡ”зҡ„е®ҡд№үпјҢж»Ўи¶іиҝҷдәӣжқЎд»¶е°ұзӣёеҪ“дәҺи®©дёӢйқўзҡ„ејҸеӯҗжҖ»жҳҜжҲҗз«Ӣпјҡ
yi[(wВ·xi)+b]вүҘ1 (i=1,2,вҖҰ,l) пјҲlжҳҜжҖ»зҡ„ж ·жң¬ж•°пјү
дҪҶжҲ‘д»¬еёёеёёд№ жғҜи®©ејҸеӯҗзҡ„еҖје’Ң0жҜ”иҫғпјҢеӣ иҖҢз»Ҹеёёз”ЁеҸҳжҚўиҝҮзҡ„еҪўејҸпјҡ
yi[(wВ·xi)+b]-1вүҘ0 (i=1,2,вҖҰ,l) пјҲlжҳҜжҖ»зҡ„ж ·жң¬ж•°пјү
еӣ жӯӨжҲ‘们зҡ„дёӨзұ»еҲҶзұ»й—®йўҳд№ҹиў«жҲ‘们иҪ¬еҢ–жҲҗдәҶе®ғзҡ„ж•°еӯҰеҪўејҸпјҢдёҖдёӘеёҰзәҰжқҹзҡ„жңҖе°ҸеҖјзҡ„й—®йўҳпјҡ
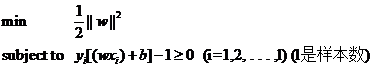
дёӢдёҖиҠӮжҲ‘们д»ҺжңҖдёҖиҲ¬зҡ„ж„Ҹд№үдёҠзңӢзңӢдёҖдёӘжұӮжңҖе°ҸеҖјзҡ„й—®йўҳжңүдҪ•зү№еҫҒпјҢд»ҘеҸҠеҰӮдҪ•жқҘи§ЈгҖӮ
еҲҶдә«еҲ°пјҡ









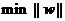
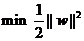 (ејҸ1)
(ејҸ1)

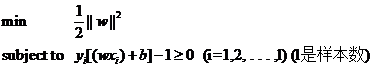



зӣёе…іжҺЁиҚҗ
然иҖҢпјҢзәҝжҖ§еҲҶзұ»еҷЁеңЁеӨ„зҗҶйқһзәҝжҖ§й—®йўҳж—¶иЎЁзҺ°йҖҡеёёиҫғе·®пјҢеӣ дёәе®ғд»¬ж— жі•жҚ•жҚүеҲ°иҫ“е…Ҙзү№еҫҒд№Ӣй—ҙеӨҚжқӮзҡ„дәӨдә’ж•Ҳеә”пјҢеҜјиҮҙжӢҹеҗҲж•ҲжһңзӣёеҜ№иҫғејұгҖӮ зӣёжҜ”д№ӢдёӢпјҢйқһзәҝжҖ§еҲҶзұ»еҷЁпјҢеҰӮеҶізӯ–ж ‘гҖҒйҡҸжңәжЈ®жһ—пјҲRFпјүгҖҒжўҜеәҰжҸҗеҚҮеҶізӯ–ж ‘пјҲGBDTпјүе’ҢеӨҡеұӮж„ҹзҹҘ...
SVMзҡ„ж ёеҝғжҖқжғіжҳҜжһ„йҖ жңҖеӨ§иҫ№и·қеҲҶзұ»еҷЁпјҢеҚіжүҫеҲ°дёҖдёӘиғҪеӨҹе°ҶдёӨзұ»ж•°жҚ®еҲҶйҡ”ејҖзҡ„жңҖеӨ§й—ҙйҡ”зҡ„еҶізӯ–иҫ№з•ҢгҖӮеңЁдәҢз»ҙз©әй—ҙдёӯпјҢиҝҷдёӘиҫ№з•Ңе°ұжҳҜдёҖдёӘзәҝжҖ§еҮҪж•°пјӣеңЁй«ҳз»ҙз©әй—ҙдёӯпјҢе®ғеҸҜиғҪжҳҜдёҖдёӘи¶…е№ійқўгҖӮйҖҡиҝҮеј•е…Ҙж ёеҮҪж•°пјҢйқһзәҝжҖ§еҸҜеҲҶзҡ„й—®йўҳд№ҹиғҪиў«...
з®ҖеҚ•зҡ„SVMзәҝжҖ§еҲҶзұ»зҡ„д»ҝзңҹе®һйӘҢпјҢеҢ…жӢ¬жөӢиҜ•ж•°жҚ®и·ҹжәҗз ҒпјҢжҳ“еӯҰ
зәҝжҖ§еҲҶзұ»еҷЁдёҺзәҝжҖ§ж”ҜжҢҒеҗ‘йҮҸжңәпјҲSVMпјүжҳҜжңәеҷЁеӯҰд№ йўҶеҹҹдёӯдёӨз§ҚйҮҚиҰҒзҡ„з®—жі•пјҢдё»иҰҒз”ЁдәҺи§ЈеҶідәҢеҲҶзұ»й—®йўҳгҖӮжң¬ж–Үе°Ҷж·ұе…ҘжҺўи®ЁиҝҷдёӨз§Қж–№жі•пјҢ并йҖҡиҝҮMatlabд»Јз ҒиҝӣиЎҢжј”зӨәгҖӮ зәҝжҖ§еҲҶзұ»еҷЁжҳҜдёҖз§ҚеҹәдәҺзү№еҫҒзҡ„з®ҖеҚ•еҲҶзұ»жЁЎеһӢпјҢе®ғйҖҡиҝҮжһ„е»әдёҖдёӘ...
SVMзҡ„ж•°жҚ®еҲҶзұ»йў„жөӢвҖ”ж„ҸеӨ§еҲ©и‘Ўиҗ„й…’з§Қзұ»иҜҶеҲ«зҡ„matlabжәҗзЁӢеәҸдёҺж•°жҚ® - SVM prediction data classification - Italian Wine type recognition matlab source code and data
ж Үйўҳдёӯзҡ„вҖңеҹәдәҺSVMзҡ„ж•°жҚ®еҲҶзұ»йў„жөӢвҖ”вҖ”ж„ҸеӨ§еҲ©и‘Ўиҗ„й…’з§Қзұ»иҜҶеҲ«вҖқжҳҜжҢҮдҪҝз”Ёж”ҜжҢҒеҗ‘йҮҸжңәпјҲSupport Vector Machine, SVMпјүз®—жі•еҜ№ж„ҸеӨ§еҲ©и‘Ўиҗ„й…’зҡ„з§Қзұ»иҝӣиЎҢйў„жөӢзҡ„дёҖз§Қж•°жҚ®еҲҶжһҗж–№жі•гҖӮSVMжҳҜдёҖз§Қзӣ‘зқЈеӯҰд№ жЁЎеһӢпјҢе°Өе…¶еңЁеӨ„зҗҶе°Ҹж ·жң¬гҖҒ...
еӣӣз§ҚжөҒиЎҢзҡ„SVMеҲҶзұ»еҷЁе·Ҙе…·з®ұпјҢеҫҲе…ЁгҖӮrar
1. SVM зәҝжҖ§еҲҶзұ»пјҡеҪ“ж•°жҚ®йӣҶеҸҜд»Ҙиў«дёҖдёӘзәҝжҖ§иҫ№з•ҢжҳҺзЎ®ең°еҲҶеүІж—¶пјҢSVM дҪҝз”ЁзәҝжҖ§ж ёеҮҪж•°жқҘеҲӣе»әеҶізӯ–иҫ№з•ҢгҖӮзәҝжҖ§SVMйҖҡиҝҮеҜ»жүҫжңҖеӨ§иҫ№и·қи¶…е№ійқўиҝӣиЎҢеҲҶзұ»пјҢиҝҷдёӘи¶…е№ійқўжҳҜи·қзҰ»еҗ„зұ»еҲ«жңҖиҝ‘зҡ„ж•°жҚ®зӮ№пјҲж”ҜжҢҒеҗ‘йҮҸпјүеҲ°е®ғзҡ„и·қзҰ»жңҖеӨ§гҖӮзәҝжҖ§SVM...
еңЁиҝҷдёӘиҝҮзЁӢдёӯпјҢжӢүж јжң—ж—Ҙд№ҳеӯҗиў«з”ЁжқҘеӨ„зҗҶзәҰжқҹжқЎд»¶пјҢеҗҢж—¶пјҢж ёеҮҪж•°иў«еј•е…ҘпјҢе®ғиғҪеӨҹе°ҶдҪҺз»ҙзҡ„йқһзәҝжҖ§й—®йўҳиҪ¬еҢ–дёәй«ҳз»ҙзҡ„зәҝжҖ§й—®йўҳпјҢд»ҺиҖҢе®һзҺ°йқһзәҝжҖ§еҲҶзұ»гҖӮ еҪ“ж•°жҚ®дёҚжҳҜзәҝжҖ§еҸҜеҲҶж—¶пјҢйқһзәҝжҖ§SVMе°ұжҳҫеҫ—е°ӨдёәйҮҚиҰҒгҖӮйқһзәҝжҖ§SVMйҖҡиҝҮдҪҝз”Ёж ё...
1. **зәҝжҖ§еҲҶзұ»еҷЁзҡ„еҺҹзҗҶ**пјҡ - зәҝжҖ§еҲҶзұ»еҷЁпјҢеҰӮж”ҜжҢҒеҗ‘йҮҸжңәпјҲSVMпјүжҲ–ж„ҹзҹҘеҷЁпјҢйҖҡиҝҮеңЁзү№еҫҒз©әй—ҙдёӯжһ„е»әдёҖдёӘи¶…е№ійқўжқҘеҢәеҲҶдёҚеҗҢзұ»еҲ«зҡ„ж ·жң¬гҖӮиҝҷдёӘи¶…е№ійқўжҳҜдҪҝеҫ—дёӨзұ»ж ·жң¬й—ҙйҡ”жңҖеӨ§зҡ„йӮЈдёӘиҫ№з•ҢгҖӮ - SVMйҖҡиҝҮжңҖеӨ§еҢ–вҖңй—ҙйҡ”вҖқпјҲmargin...
еңЁиҝҷдёӘвҖңзәҝжҖ§еҲҶзұ»еҷЁд»Јз ҒвҖқеҺӢзј©еҢ…дёӯпјҢжҲ‘们еҫҲеҸҜиғҪдјҡжүҫеҲ°дҪҝз”ЁPythonе®һзҺ°зҡ„зәҝжҖ§еҲҶзұ»еҷЁзӨәдҫӢпјҢдҫӢеҰӮйҖ»иҫ‘еӣһеҪ’гҖҒж”ҜжҢҒеҗ‘йҮҸжңәпјҲSVMпјүжҲ–иҖ…зәҝжҖ§еҲӨеҲ«еҲҶжһҗпјҲLDAпјүгҖӮиҝҷдәӣжЁЎеһӢйғҪеҹәдәҺж•°жҚ®зҡ„зәҝжҖ§зү№жҖ§иҝӣиЎҢйў„жөӢпјҢ并且еңЁиҜёеҰӮдәҢеҲҶзұ»жҲ–еӨҡе…ғ...
йҮҮз”ЁmatlabиҝӣиЎҢж”ҜжҢҒеҗ‘йҮҸжңәsvmзҡ„зәҝжҖ§еҲҶзұ»пјҢжҜҸдёҖеҸҘйғҪжңүиҜҰе°Ҫзҡ„и§ЈйҮҠпјҢж–№дҫҝеӨ§е®¶еӯҰд№ дәӨжөҒ
LDAиҜ•еӣҫжүҫеҲ°дёҖдёӘеҲҶзұ»й—ҙйҡ”жңҖеӨ§еҢ–зҡ„и¶…е№ійқўпјҢиҖҢSVMеҲҷеҜ»жүҫжңҖе®Ҫзҡ„й—ҙйҡ”пјҢ并引е…ҘдәҶж ёжҠҖе·§жқҘеӨ„зҗҶйқһзәҝжҖ§й—®йўҳгҖӮ еңЁPythonдёӯпјҢжҲ‘们еҸҜд»ҘдҪҝз”Ёnumpyзҡ„зҹ©йҳөиҝҗз®—жқҘе®һзҺ°зәҝжҖ§жЁЎеһӢгҖӮйҰ–е…ҲпјҢжҲ‘们йңҖиҰҒеҮҶеӨҮж•°жҚ®йӣҶпјҢеҢ…жӢ¬зү№еҫҒзҹ©йҳөXе’ҢеҜ№еә”зҡ„...
ж Үйўҳдёӯзҡ„"SVM.rar_X6W_svm еҲҶзұ»_svmйқһзәҝжҖ§еҲҶзұ»_йқһзәҝжҖ§svm"жҡ—зӨәдәҶжҲ‘们讨и®әзҡ„дё»йўҳжҳҜе…ідәҺеҰӮдҪ•еҲ©з”ЁSVMеӨ„зҗҶйқһзәҝжҖ§еҲҶзұ»й—®йўҳпјҢдё”жҳҜеҹәдәҺMATLABе№іеҸ°зҡ„е®һзҺ°гҖӮеңЁе®һйҷ…еә”з”ЁдёӯпјҢеҫҲеӨҡж•°жҚ®йӣҶ并дёҚйҒөеҫӘз®ҖеҚ•зҡ„зәҝжҖ§е…ізі»пјҢеӣ жӯӨзҗҶи§ЈйқһзәҝжҖ§...
еңЁжңәеҷЁеӯҰд№ йўҶеҹҹпјҢSVMд»Ҙе…¶дјҳз§Җзҡ„жіӣеҢ–иғҪеҠӣгҖҒеӨ„зҗҶйқһзәҝжҖ§й—®йўҳзҡ„иғҪеҠӣд»ҘеҸҠеҜ№е°Ҹж ·жң¬ж•°жҚ®зҡ„й«ҳж•ҲеҲ©з”ЁиҖҢеӨҮеҸ—жҺЁеҙҮгҖӮиҝҷж¬ҫеҗҚдёә"SVMеҲҶзұ»еҷЁ"зҡ„е·Ҙе…·жӯЈжҳҜдёәдәҶеё®еҠ©з”ЁжҲ·жӣҙеҘҪең°зҗҶи§Је’Ңеә”з”ЁSVMз®—жі•гҖӮ SVMзҡ„ж ёеҝғжҖқжғіжҳҜжүҫеҲ°дёҖдёӘжңҖдјҳи¶…е№ійқўпјҢ...
SVMзҡ„еҸӮж•°дјҳеҢ–вҖ”вҖ”еҰӮдҪ•жӣҙеҘҪзҡ„жҸҗеҚҮеҲҶзұ»еҷЁзҡ„жҖ§иғҪ.7zжң¬з« иҰҒи§ЈеҶізҡ„й—®йўҳе°ұжҳҜд»…д»…еҲ©з”Ёи®ӯз»ғйӣҶжүҫеҲ°еҲҶзұ»зҡ„жңҖдҪіеҸӮж•°пјҢдёҚдҪҶиғҪеӨҹй«ҳеҮҶзЎ®зҺҮзҡ„йў„жөӢи®ӯз»ғйӣҶиҖҢдё”иҰҒеҗҲзҗҶзҡ„йў„жөӢжөӢиҜ•йӣҶпјҢдҪҝеҫ—жөӢиҜ•йӣҶзҡ„еҲҶзұ»еҮҶзЎ®зҺҮд№ҹз»ҙжҢҒеңЁдёҖдёӘиҫғй«ҳж°ҙе№іпјҢеҚі...
еңЁеӨҡзұ»еҲҶзұ»еҷЁзҡ„еңәжҷҜдёӢпјҢSVMйҖҡиҝҮжү©еұ•е…¶еҹәжң¬зҡ„дёӨзұ»еҲҶзұ»иғҪеҠӣжқҘеӨ„зҗҶеӨҡдәҺдёӨдёӘзұ»еҲ«зҡ„й—®йўҳгҖӮиҝҷдёӘеҺӢзј©еҢ…жҸҗдҫӣзҡ„иө„жәҗеә”иҜҘеҢ…еҗ«е®һзҺ°еӨҡзұ»SVMзҡ„жәҗд»Јз ҒпјҢд»ҘеҸҠе…ідәҺеҰӮдҪ•еә”з”Ёе’ҢзҗҶи§Јиҝҷдәӣд»Јз Ғзҡ„иҜҰз»ҶжҢҮеҚ—пјҢеҜ№дәҺеӯҰд№ е’Ңе®һи·өSVMзҡ„еҲқеӯҰиҖ…жқҘиҜҙ...
д»ҺжҸҗдҫӣзҡ„еҶ…е®№дёӯпјҢжҲ‘们еҸҜд»ҘзңӢеҲ°пјҢжңүе…ідәҺеҰӮдҪ•дҪҝз”ЁMATLABд»Јз ҒжқҘе®һзҺ°йқһзәҝжҖ§SVMеҲҶзұ»еҷЁзҡ„жҸҸиҝ°гҖӮд»Јз ҒдёӯеҢ…еҗ«дәҶеҰӮдҪ•еҠ иҪҪж•°жҚ®пјҢи®ҫзҪ®ж ёеҮҪж•°е’ҢеҸӮж•°пјҢи®ӯз»ғеҲҶзұ»еҷЁд»ҘеҸҠеҰӮдҪ•з»ҳеҲ¶еҲҶзұ»з»“жһңгҖӮ жңҖеҗҺпјҢдёәдәҶиҜ„дј°жүҖи®ҫи®Ўзҡ„SVMеҲҶзұ»еҷЁзҡ„жҖ§иғҪпјҢ...
жҸҸиҝ°дёӯжҸҗеҲ°зҡ„"svmnonlinear"ж ҮзӯҫпјҢж„Ҹе‘ізқҖжҲ‘们е°Ҷи®Ёи®әеҰӮдҪ•йҖҡиҝҮSVMеӨ„зҗҶйқһзәҝжҖ§й—®йўҳгҖӮ SVMзҡ„ж ёеҝғжҖқжғіжҳҜжүҫеҲ°дёҖдёӘжңҖеӨ§иҫ№и·қи¶…е№ійқўпјҢиҝҷдёӘи¶…е№ійқўиғҪеӨҹжңҖеӨ§еҢ–дёӨзұ»ж ·жң¬д№Ӣй—ҙзҡ„й—ҙйҡ”гҖӮеңЁйқһзәҝжҖ§жғ…еҶөдёӢпјҢSVMеҲ©з”Ёж ёеҮҪж•°пјҲKernel Trick...
**ж”ҜжҢҒеҗ‘йҮҸжңәпјҲSupport Vector MachineпјҢз®Җз§°SVMпјү**жҳҜдёҖз§Қе№ҝжіӣеә”з”Ёзҡ„зӣ‘зқЈеӯҰд№ з®—жі•пјҢе°Өе…¶еңЁдәҢеҲҶзұ»й—®йўҳдёӯиЎЁзҺ°еҮәиүІгҖӮзәҝжҖ§SVMжҳҜSVMзҡ„дёҖз§ҚеҪўејҸпјҢе®ғйҖҡиҝҮжүҫеҲ°дёҖдёӘжңҖдјҳи¶…е№ійқўжқҘеҜ№ж•°жҚ®иҝӣиЎҢзәҝжҖ§еҲ’еҲҶгҖӮеңЁиҝҷдёӘеңәжҷҜдёӢпјҢжҲ‘们讨и®ә...