摘自:
http://www.blogjava.net/zhenandaci/archive/2009/02/14/254630.html
从最一般的定义上说,一个求最小值的问题就是一个优化问题(也叫寻优问题,更文绉绉的叫法是规划——Programming),它同样由两部分组成,目标函数和约束条件,可以用下面的式子表示:
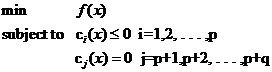
(式1)
约束条件用函数c来表示,就是constrain的意思啦。你可以看出一共有p+q个约束条件,其中p个是不等式约束,q个等式约束。
关于这个式子可以这样来理解:式中的x是自变量,但不限定它的维数必须为1(视乎你解决的问题空间维数,对我们的文本分类来说,那可是成千上万啊)。要求f(x)在哪一点上取得最小值(反倒不太关心这个最小值到底是多少,关键是哪一点),但不是在整个空间里找,而是在约束条件所划定的一个有限的空间里找,这个有限的空间就是优化理论里所说的可行域。注意可行域中的每一个点都要求满足所有p+q个条件,而不是满足其中一条或几条就可以(切记,要满足每个约束),同时可行域边界上的点有一个额外好的特性,它们可以使不等式约束取得等号!而边界内的点不行。
关于可行域还有个概念不得不提,那就是凸集,凸集是指有这么一个点的集合,其中任取两个点连一条直线,这条线上的点仍然在这个集合内部,因此说“凸”是很形象的(一个反例是,二维平面上,一个月牙形的区域就不是凸集,你随便就可以找到两个点违反了刚才的规定)。
回头再来看我们线性分类器问题的描述,可以看出更多的东西。
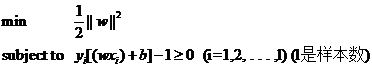
(式2)
在这个问题中,自变量就是w,而目标函数是w的二次函数,所有的约束条件都是w的线性函数(哎,千万不要把xi当成变量,它代表样本,是已知的),这种规划问题有个很有名气的称呼——二次规划(Quadratic Programming,QP),而且可以更进一步的说,由于它的可行域是一个凸集,因此它是一个凸二次规划。
一下子提了这么多术语,实在不是为了让大家以后能向别人炫耀学识的渊博,这其实是我们继续下去的一个重要前提,因为在动手求一个问题的解之前(好吧,我承认,是动计算机求……),我们必须先问自己:这个问题是不是有解?如果有解,是否能找到?
对于一般意义上的规划问题,两个问题的答案都是不一定,但凸二次规划让人喜欢的地方就在于,它有解(教科书里面为了严谨,常常加限定成分,说它有全局最优解,由于我们想找的本来就是全局最优的解,所以不加也罢),而且可以找到!(当然,依据你使用的算法不同,找到这个解的速度,行话叫收敛速度,会有所不同)
对比(式2)和(式1)还可以发现,我们的线性分类器问题只有不等式约束,因此形式上看似乎比一般意义上的规划问题要简单,但解起来却并非如此。
因为我们实际上并不知道该怎么解一个带约束的优化问题。如果你仔细回忆一下高等数学的知识,会记得我们可以轻松的解一个不带任何约束的优化问题(实际上就是当年背得烂熟的函数求极值嘛,求导再找0点呗,谁不会啊?笑),我们甚至还会解一个只带等式约束的优化问题,也是背得烂熟的,求条件极值,记得么,通过添加拉格朗日乘子,构造拉格朗日函数,来把这个问题转化为无约束的优化问题云云(如果你一时没想通,我提醒一下,构造出的拉格朗日函数就是转化之后的问题形式,它显然没有带任何条件)。
读者问:如果只带等式约束的问题可以转化为无约束的问题而得以求解,那么可不可以把带不等式约束的问题向只带等式约束的问题转化一下而得以求解呢?
聪明,可以,实际上我们也正是这么做的。下一节就来说说如何做这个转化,一旦转化完成,求解对任何学过高等数学的人来说,都是小菜一碟啦。
分享到:








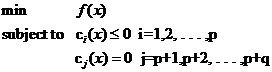 (式1)
(式1)
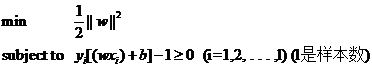 (式2)
(式2)



相关推荐
然而,线性分类器在处理非线性问题时表现通常较差,因为它们无法捕捉到输入特征之间复杂的交互效应,导致拟合效果相对较弱。 相比之下,非线性分类器,如决策树、随机森林(RF)、梯度提升决策树(GBDT)和多层感知...
2. **创建SVM模型**:使用`fitcsvm`函数创建SVM分类器。例如: ```matlab model = fitcsvm(X, y); ``` 其中,`X`是特征矩阵,`y`是对应的类别标签。 3. **选择内核和参数**:默认情况下,Matlab会选择一个合适...
简单的SVM线性分类的仿真实验,包括测试数据跟源码,易学
线性分类器与线性支持向量机(SVM)是机器学习领域中两种重要的算法,主要用于解决二分类问题。本文将深入探讨这两种方法,并通过Matlab代码进行演示。 线性分类器是一种基于特征的简单分类模型,它通过构建一个...
SVM的数据分类预测—意大利葡萄酒种类识别的matlab源程序与数据 - SVM prediction data classification - Italian Wine type recognition matlab source code and data
标题中的“基于SVM的数据分类预测——意大利葡萄酒种类识别”是指使用支持向量机(Support Vector Machine, SVM)算法对意大利葡萄酒的种类进行预测的一种数据分析方法。SVM是一种监督学习模型,尤其在处理小样本、...
2. SVM 非线性分类:对于非线性可分的数据,SVM 采用核技巧(Kernel Trick)。它将原始数据映射到高维空间,在这个空间中原本不可分的数据可能变得可分。高斯核(也称为径向基函数RBF)是常用的非线性核函数之一,它...
在这个过程中,拉格朗日乘子被用来处理约束条件,同时,核函数被引入,它能够将低维的非线性问题转化为高维的线性问题,从而实现非线性分类。 当数据不是线性可分时,非线性SVM就显得尤为重要。非线性SVM通过使用核...
### SVM入门(五)线性分类器的求解——问题的描述Part2 #### 重要概念与背景 本文档旨在帮助读者理解支持向量机(SVM)中的线性分类器求解过程及其数学表述,特别关注于如何将线性分类器问题转化为优化问题,并讨论...
线性分类器在模式识别中扮演着至关重要的角色,它是一种简单而强大的工具,尤其适用于数据分布具有线性边界的场景。在这个主题中,我们将深入探讨线性分类器的理论基础,以及如何在MATLAB环境中进行实现。我们将重点...
采用matlab进行支持向量机svm的线性分类,每一句都有详尽的解释,方便大家学习交流
在这个“线性分类器代码”压缩包中,我们很可能会找到使用Python实现的线性分类器示例,例如逻辑回归、支持向量机(SVM)或者线性判别分析(LDA)。这些模型都基于数据的线性特性进行预测,并且在诸如二分类或多元...
标题中的"SVM.rar_X6W_svm 分类_svm非线性分类_非线性svm"暗示了我们讨论的主题是关于如何利用SVM处理非线性分类问题,且是基于MATLAB平台的实现。在实际应用中,很多数据集并不遵循简单的线性关系,因此理解非线性...
LDA试图找到一个分类间隔最大化的超平面,而SVM则寻找最宽的间隔,并引入了核技巧来处理非线性问题。 在Python中,我们可以使用numpy的矩阵运算来实现线性模型。首先,我们需要准备数据集,包括特征矩阵X和对应的...
SVM的参数优化——如何更好的提升分类器的性能.7z本章要解决的问题就是仅仅利用训练集找到分类的最佳参数,不但能够高准确率的预测训练集而且要合理的预测测试集,使得测试集的分类准确率也维持在一个较高水平,即...
在机器学习领域,SVM以其优秀的泛化能力、处理非线性问题的能力以及对小样本数据的高效利用而备受推崇。这款名为"SVM分类器"的工具正是为了帮助用户更好地理解和应用SVM算法。 SVM的核心思想是找到一个最优超平面,...
在多类分类器的场景下,SVM通过扩展其基本的两类分类能力来处理多于两个类别的问题。这个压缩包提供的资源应该包含实现多类SVM的源代码,以及关于如何应用和理解这些代码的详细指南,对于学习和实践SVM的初学者来说...
从提供的内容中,我们可以看到,有关于如何使用MATLAB代码来实现非线性SVM分类器的描述。代码中包含了如何加载数据,设置核函数和参数,训练分类器以及如何绘制分类结果。 最后,为了评估所设计的SVM分类器的性能,...
**支持向量机(Support Vector Machine,简称SVM)**是一种广泛应用的监督学习算法,尤其在二分类问题中表现出色。线性SVM是SVM的一种形式,它通过找到一个最优超平面来对数据进行线性划分。在这个场景下,我们讨论...
描述中提到的"svmnonlinear"标签,意味着我们将讨论如何通过SVM处理非线性问题。 SVM的核心思想是找到一个最大边距超平面,这个超平面能够最大化两类样本之间的间隔。在非线性情况下,SVM利用核函数(Kernel Trick...