µÄÆÕ║Åń«Śµ│ĢÕ»╣ń╗ōµ×£ńÜäÕö»õĖĆĶ”üµ▒éÕ░▒µś»µōŹõĮ£µĢ░µ╗ĪĶČ│Õģ©Õ║ÅÕģ│ń│╗’╝Ü
- Õ”éµ×£ aŌēżb Õ╣ČõĖö bŌēżc ķéŻõ╣ł aŌēżc’╝łõ╝ĀķĆÆµĆ¦’╝ēŃĆé
- Õ»╣õ║Ä a µł¢ b’╝īĶ”üõĖŹ aŌēżb’╝īĶ”üõĖŹ bŌēża’╝łÕ«īÕģ©µĆ¦’╝ēŃĆé
Ķ┐ÖõĖ¬ķŚ«ķóśÕÅ»õ╗źńö©õ┐Īµü»Ķ«║µØźÕø×ńŁöŃĆé
µłæõ╗Ä 1 Õł░ 5 õĖŁµīæõĖĆõĖ¬µĢ░ÕŁŚÕć║µØźĶ«®õĮĀµØźńī£’╝īµ»ÅÕø×ÕÉłõĮĀķāĮÕÅ»õ╗źķŚ«µłæõĖĆõĖ¬ķŚ«ķóś’╝īµłæńÜäÕø×ńŁöŌĆ£µś»ŌĆصł¢ŌĆ£õĖŹµś»ŌĆØ’╝ł1 µł¢ 0’╝ē’╝īķéŻõ╣łõĮĀĶć│Õ░æķ£ĆĶ”üÕćĀõĖ¬Õø×ÕÉłµēŹĶāĮõ┐ØĶ»üńī£Õć║Ķ┐ÖõĖ¬µĢ░ÕŁŚ’╝¤
µ»öĶŠāń¼”ÕÉłĶ┐ÖõĖ¬µĖĖµłÅń▓Šńź×ńÜäńÄ®µ│Ģµś»õ╗ÄĶć¬ÕĘ▒ńÜäÕ╣ĖĶ┐ɵĢ░ÕŁŚ’╝łµ»öÕ”éµłæńÜ䵜»7’╝ēÕ╝ĆÕ¦ŗńī£ĶĄĘ’╝īõĖĆõĖ¬õĖĆõĖ¬Õ£░ķŚ«µłæŌĆ£µś»õĖŹµś»X’╝¤ŌĆØ’╝ī ÕÅ»ĶāĮõĮĀńÜäĶ┐ɵ░öĶČ│Õż¤ÕźĮ’╝īõĖĆõĖ¬Õø×ÕÉłÕ░▒ĶāĮÕż¤ńī£Õ»╣’╝īõĮåµś»Õ£©µ£ĆÕØÅńÜäµāģÕåĄõĖŗÕÅ»ĶāĮÕ░▒ķ£ĆĶ”ü5õĖ¬Õø×ÕÉł’╝īµēĆõ╗źõĮĀńÜäńŁöµĪłÕ║öĶ»źµś»ŌĆ£Ķć│Õ░æķ£ĆĶ”ü5õĖ¬Õø×ÕÉłŌĆØ ’╝łõ║ŗÕ«×õĖŖõĮĀĶć│Õ░æÕŬķ£ĆĶ”üõĖƵ¼ĪÕ░▒ŌĆ£µ£ēÕÅ»ĶāĮŌĆØńī£Õć║µØź’╝īõĮåõĖ║õ║åŌĆ£õ┐ØĶ»üĶāĮŌĆØńī£Õć║µØź’╝īõĮĀÕÅ¬ÕźĮÕ¦öµø▓µ▒éÕģ©Õ£░Ķ»┤ 5’╝ē’╝ī µŹóÕÅźĶ»ØĶ»┤Ķ┐Öń¦Źńī£µ│ĢńÜäµ£Ćõ╝śõĖŗńĢīµś» 5ŃĆé ’╝łÕ╣│ÕØćµĆ¦ĶāĮµś» 1├Ś1/5+2├Ś1/5+ŌĆ”+5├Ś1/5=’╝ł1+ŌĆ”+5’╝ē/5 = 3’╝ē
õĮåÕøĀõĖ║õĮĀõ╝Üõ║īÕłå’╝īµēĆõ╗źõ╝ÜĶ┐ÖµĀĘķŚ«ŌĆ£µś»õĖŹµś»µ»ö3Õż¦’╝¤ŌĆØŌĆ”ŌĆ”ĶĆīõĖöµŚĀĶ«║µłæµīæÕć║ńÜäµĢ░ÕŁŚµś»ÕćĀ’╝īķāĮÕŬńö©3õĖ¬Õø×ÕÉłŃĆé┬Āõ║īÕłåµśŠńäȵś»õĖĆń¦Źµø┤õĮ│ńÜäńŁ¢ńĢź’╝īķéŻõ╣łÕ«āÕźĮÕ£©õ╗Ćõ╣łÕ£░µ¢╣Õæó’╝¤ ńö©õ┐Īµü»Ķ«║ńÉåĶ¦Ż:┬Āµ£ĆÕż¦ńÜäńåĄŃĆé
Ķŗ▒µ¢ćńēłń╗┤Õ¤║ńÖŠń¦æĶ»ŹµØĪµ£ēõĖ¬Õż¦Ķć┤ńÜäĶ¦ŻķćŖ’╝ÜComparison_sort’╝ī µ£ĆÕ░æµ¼ĪµĢ░õĖ║ log(5!) = 6.91’╝īÕÅ¢µĢ┤ńÜäĶ»Ø’╝īÕ░▒µś» 7ŃĆé
Õå│ńŁ¢µĀæÕ”éõĖŗ’╝Ü
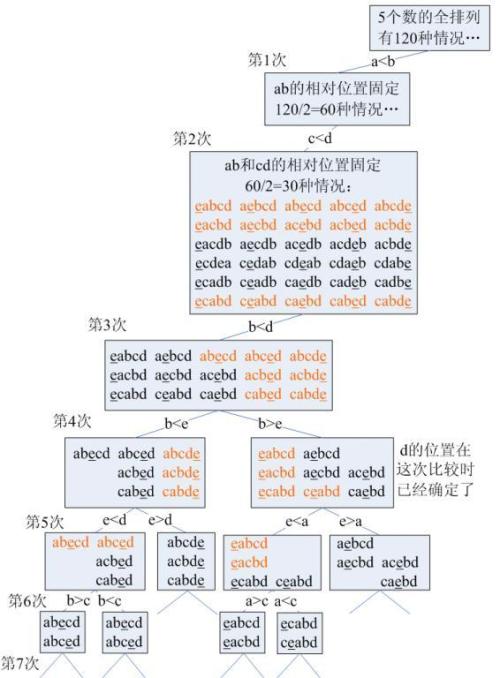
Õ”éµ×£µłæõ╗¼ńö©ÕĮÆÕ╣ȵÄÆÕ║ÅńÜäĶ»Ø’╝īµ»öĶŠāµ¼ĪµĢ░µś»O’╝łnlogn’╝ē’╝īÕøĀõĖ║ÕĮÆÕ╣ȵÄÆÕ║ŵś»┬ĀÕģ©Õ▒Ƶ£Ćõ╝śĶ¦Ż’╝īõĮåµś»Õ£©Õ▒Ćķā©’╝īÕĮÆÕ╣ČÕ╣ČõĖŹķāĮõ┐ØĶ»üµś»µ£Ćõ╝śńÜäŃĆé
ķÖäõĖĆÕ╝ĀÕ┐½ķƤµÄÆÕ║ÅńÜä gif ÕøŠ’╝Ü

ńøĖÕģ│ķśģĶ»╗’╝Ü










ńøĖÕģ│µÄ©ĶŹÉ
ķĆÜĶ┐ćķĆēÕÅ¢õĖĆõĖ¬ŌĆ£Õ¤║ÕćåŌĆØÕģāń┤Ā’╝īÕ░åÕ║ÅÕłŚÕłÆÕłåõĖ║õĖżķā©Õłå’╝īõĮ┐ÕŠŚõĖĆķā©ÕłåńÜäµēƵ£ēÕģāń┤ĀķāĮÕ░Åõ║ÄÕÅ”õĖĆķā©Õłå’╝īńäČÕÉÄķĆÆÕĮÆÕ£░Õ»╣Ķ┐ÖõĖżķā©ÕłåĶ┐øĶĪīµÄÆÕ║ÅŃĆéÕ┐½ķƤµÄÆÕ║ÅńÜäÕ╣│ÕØ浌ČķŚ┤ÕżŹµØéÕ║”õĖ║O(n log n)’╝īõĮåÕ£©µ£ĆÕØŵāģÕåĄõĖŗ’╝łĶŠōÕģźÕĘ▓µÄÆÕ║ŵł¢ÕÅŹÕÉæµÄÆÕ║Å’╝ēõĖ║O(n^2)ŃĆé ...
Ķ┐Öń»ćµ¢ćń½ĀõĖ╗Ķ”üõ╗ŗń╗Źõ║åõĖĆõĖ¬Õ¤║õ║Ä Delphi Õ╝ĆÕÅæńÜäĶĮ»õ╗Č’╝īńö©õ║ÄÕŖ©µĆüÕøŠńż║Õłåµ×ÉÕÆīµ╝öńż║35ń¦ŹõĖŹÕÉīńÜäÕ¤║õ║ĵ»öĶŠāńÜäÕåģķā©µÄÆÕ║Åń«Śµ│ĢŃĆéÕåģķā©µÄÆÕ║ŵś»µīćµĢ░µŹ«Ķ«░ÕĮĢÕ£©ÕåģÕŁśõĖŁĶ┐øĶĪīńÜäµÄÆÕ║ÅĶ┐ćń©ŗ’╝īõĖŹµČēÕÅŖÕż¢ķā©ÕŁśÕé©ÕÖ©ŃĆéõ╗źõĖŗµś»Õ»╣Ķ┐Öõ║øń«Śµ│ĢńÜäĶ»”ń╗åĶ»┤µśÄ’╝Ü 1. **...
ķĆēµŗ®µÄÆÕ║Åń«Śµ│Ģµś»Õ¤║õ║ÄCĶ»ŁĶ©ĆÕ«×ńÄ░ńÜäõĖĆń¦ŹÕ¤║ńĪƵÄÆÕ║Åń«Śµ│Ģ’╝īÕģČÕ¤║µ£¼µĆصā│µś»’╝Üķ”¢Õģłõ╗ÄÕŠģµÄÆÕ║ÅÕ║ÅÕłŚõĖŁķĆēÕć║µ£ĆÕ░Å’╝łµł¢µ£ĆÕż¦’╝ēńÜäõĖĆõĖ¬Õģāń┤Ā’╝īÕŁśµöŠÕł░µÄÆÕ║ÅÕ║ÅÕłŚńÜäĶĄĘÕ¦ŗõĮŹńĮ«’╝īńäČÕÉÄÕåŹõ╗ÄÕē®õĮÖµ£¬µÄÆÕ║ÅÕģāń┤ĀõĖŁń╗¦ń╗ŁÕ»╗µēŠµ£ĆÕ░Å’╝łµł¢µ£ĆÕż¦’╝ēÕģāń┤Ā’╝īõ╗źµŁżń▒╗µÄ©’╝ī...
Ķ┐ÖõĖ¬ķĪ╣ńø«"Õ¤║õ║ÄMFCńÜäÕåģµÄÆÕ║Åń«Śµ│ĢÕŖ©µĆüµ╝öńż║"µś»õĖĆõĖ¬µĢÖÕŁ”ÕĘźÕģĘ’╝īÕ«āķĆÜĶ┐ćÕÅ»Ķ¦åÕī¢ńÜäµ¢╣Õ╝Å’╝īÕĖ«ÕŖ®ńö©µłĘńÉåĶ¦ŻÕ╣ȵ»öĶŠāÕżÜń¦ŹÕåģµÄÆÕ║Åń«Śµ│ĢńÜäµē¦ĶĪīĶ┐ćń©ŗŃĆé **ÕåģµÄÆÕ║Åń«Śµ│Ģ** ÕåģµÄÆÕ║ŵś»µīćµĢ░µŹ«Ķ«░ÕĮĢÕ£©ÕåģÕŁśõĖŁĶ┐øĶĪīµÄÆÕ║Å’╝īÕīģµŗ¼õĮåõĖŹķÖÉõ║Äõ╗źõĖŗÕćĀń¦ŹÕĖĖĶ¦üń«Śµ│Ģ...
Õ£©µĘ▒ÕģźÕłåµ×ÉĶ┐Öń»ćµĀćķóśõĖ║ŌĆ£Õ¤║õ║ÄFPGAńÜäÕ╣ČĶĪīÕģ©µ»öĶŠāµÄÆÕ║Åń«Śµ│ĢŌĆØńÜäµ¢ćń½Āõ╣ŗÕēŹ’╝īÕģłµśÄńĪ«ÕćĀõĖ¬Õģ│ķö«ńé╣’╝ÜFPGA’╝łField-Programmable Gate Array’╝īńÄ░Õ£║ÕÅ»ń╝¢ń©ŗķŚ©ķśĄÕłŚ’╝ē’╝īÕ╣ČĶĪīÕżäńÉåÕÆīµÄÆÕ║Åń«Śµ│ĢŃĆéFPGAµś»õĖĆń¦ŹÕÅ»õ╗źķĆÜĶ┐ćń╝¢ń©ŗµØźķģŹńĮ«ńÜäķøåµłÉńöĄĶĘ»’╝ī...
7. **ÕĖīÕ░öµÄÆÕ║Å**’╝ܵö╣Ķ┐øńÜäµÅÆÕģźµÄÆÕ║Å’╝īķĆÜĶ┐ćÕó×ķćÅÕ║ÅÕłŚÕ░åÕģāń┤ĀÕłåń╗äĶ┐øĶĪīµÅÆÕģźµÄÆÕ║Å’╝īµ£ĆÕÉÄĶ┐øĶĪīõĖƵ¼ĪÕģ©ĶĘØõĖ║1ńÜäµÅÆÕģźµÄÆÕ║ÅŃĆ鵌ČķŚ┤ÕżŹµØéÕ║”Õ£©µ£ĆÕźĮŃĆüµ£ĆÕØÅÕÆīÕ╣│ÕØćµāģÕåĄõĖŗķāĮõ╝śõ║Äń«ĆÕŹĢńÜäµÅÆÕģźµÄÆÕ║ÅŃĆé 8. **Ķ«ĪµĢ░µÄÆÕ║Å**ŃĆü**µĪȵÄÆÕ║Å**ÕÆī**Õ¤║µĢ░µÄÆÕ║Å**...
Õ«āńÜäÕ¤║µ£¼µĆصā│µś»ķććńö©Õłåµ▓╗µ│Ģ’╝īķĆēÕÅ¢õĖĆõĖ¬Õ¤║ÕćåÕģāń┤Ā’╝īÕ░åµĢ░ń╗äÕłåõĖ║õĖżķā©Õłå’╝īõĖĆķā©ÕłåµēƵ£ēÕģāń┤ĀķāĮÕ░Åõ║ÄÕ¤║Õćå’╝īÕÅ”õĖĆķā©ÕłåµēƵ£ēÕģāń┤ĀķāĮÕż¦õ║ÄÕ¤║Õćå’╝īńäČÕÉÄķĆÆÕĮÆÕ£░Õ»╣Ķ┐ÖõĖżķā©ÕłåĶ┐øĶĪīÕ┐½ķƤµÄÆÕ║ÅŃĆéĶ┐Öń¦Źń«Śµ│ĢÕ£©Õ╣│ÕØćµāģÕåĄõĖŗńÜ䵌ČķŚ┤ÕżŹµØéÕ║”õĖ║O(n log n)’╝īõĮåÕ£©...
ŃĆɵÄÆÕ║Åń╗ōµ×ä5ŃĆæÕ¤║õ║ĵ»öĶŠāńÜäÕåģķā©µÄÆÕ║ŵĆ╗ń╗ō Õ£©Ķ«Īń«Śµ£║ń¦æÕŁ”õĖŁ’╝īµÄÆÕ║ŵś»Õ░åõĖĆń╗äµĢ░µŹ«µīēńģ¦ńē╣Õ«ÜķĪ║Õ║ŵÄÆÕłŚńÜäĶ┐ćń©ŗŃĆéÕåģķā©µÄÆÕ║Å’╝īµł¢ń¦░õĖ║ÕåģÕŁśµÄÆÕ║Å’╝īµś»µīćµĢ░µŹ«Ķ«░ÕĮĢÕ£©ÕåģÕŁśõĖŁĶ┐øĶĪīńÜäµÄÆÕ║Å’╝īõĖÄÕż¢ķā©µÄÆÕ║Å’╝łµĢ░µŹ«ķćÅÕż¬Õż¦µŚĀµ│ĢÕģ©ķā©ĶŻģÕģźÕåģÕŁś’╝ēńøĖÕ»╣ŃĆéµ£¼...
Õ«āńÜäõĖ╗Ķ”üµĆصā│µś»ķćŹÕżŹÕ£░ĶĄ░Ķ«┐Ķ┐ćĶ”üµÄÆÕ║ÅńÜäµĢ░ÕłŚ’╝īõĖƵ¼Īµ»öĶŠāõĖżõĖ¬Õģāń┤Ā’╝īÕ”éµ×£õ╗¢õ╗¼ńÜäķĪ║Õ║ÅķöÖĶ»»Õ░▒µŖŖõ╗¢õ╗¼õ║żµŹóĶ┐ćµØźŃĆéķüŹÕÄåµĢ░ÕłŚńÜäÕĘźõĮ£µś»ķćŹÕżŹÕ£░Ķ┐øĶĪīńø┤Õł░µ▓Īµ£ēÕåŹķ£ĆĶ”üõ║żµŹó’╝īõ╣¤Õ░▒µś»Ķ»┤Ķ»źµĢ░ÕłŚÕĘ▓ń╗ŵÄÆÕ║ÅÕ«īµłÉŃĆé 2. **Õ┐½ķƤµÄÆÕ║Å**’╝Üńö▒C.A.R. ...
- **ÕĤńÉå**’╝ÜķćŹÕżŹĶĄ░Ķ«┐Ķ”üµÄÆÕ║ÅńÜäµĢ░ÕłŚ’╝īõĖƵ¼Īµ»öĶŠāõĖżõĖ¬Õģāń┤Ā’╝īÕ”éµ×£õ╗¢õ╗¼ńÜäķĪ║Õ║ÅķöÖĶ»»Õ░▒µŖŖõ╗¢õ╗¼õ║żµŹóĶ┐ćµØźŃĆéĶĄ░Ķ«┐µĢ░ÕłŚńÜäÕĘźõĮ£µś»ķćŹÕżŹĶ┐øĶĪīńÜä’╝īńø┤Õł░µ▓Īµ£ēÕåŹķ£ĆĶ”üõ║żµŹó’╝īõ╣¤Õ░▒µś»Ķ»┤Ķ»źµĢ░ÕłŚÕĘ▓ń╗ŵÄÆÕ║ÅÕ«īµłÉŃĆé - **µŚČķŚ┤ÕżŹµØéÕ║”**’╝ܵ£ĆÕźĮµāģÕåĄO(n)’╝ī...
7. **Ķ«ĪµĢ░µÄÆÕ║Å’╝łCounting Sort’╝ēŃĆüµĪȵÄÆÕ║Å’╝łBucket Sort’╝ēÕÆīÕ¤║µĢ░µÄÆÕ║Å’╝łRadix Sort’╝ē**’╝ÜĶ┐ÖõĖēń¦ŹµÄÆÕ║Åń«Śµ│ĢÕ▒×õ║ÄķØ×µ»öĶŠāÕ×ŗµÄÆÕ║Å’╝īõĖŹõŠØĶĄ¢õ║ÄÕģāń┤ĀķŚ┤ńÜäµ»öĶŠā’╝īĶĆīµś»Õ¤║õ║Äńē╣Õ«ÜńÜäńē╣µĆ¦’╝īÕ”éÕģāń┤ĀńÜäĶīāÕø┤ŃĆüÕłåÕĖāńŁēŃĆéJavaõĖŁÕ«×ńÄ░Ķ┐Öń▒╗µÄÆÕ║ÅķĆÜÕĖĖ...
ÕåƵ│ĪµÄÆÕ║ŵś»õĖĆń¦Źń«ĆÕŹĢńÜäµÄÆÕ║Åń«Śµ│Ģ’╝īÕ«āķćŹÕżŹÕ£░ķüŹÕÄåÕŠģµÄÆÕ║ÅńÜäµĢ░ÕłŚ’╝īõĖƵ¼Īµ»öĶŠāõĖżõĖ¬Õģāń┤Ā’╝īÕ”éµ×£õ╗¢õ╗¼ńÜäķĪ║Õ║ÅķöÖĶ»»Õ░▒µŖŖõ╗¢õ╗¼õ║żµŹóĶ┐ćµØźŃĆéķüŹÕÄåµĢ░ÕłŚńÜäÕĘźõĮ£µś»ķćŹÕżŹÕ£░Ķ┐øĶĪīńø┤Õł░µ▓Īµ£ēÕåŹķ£ĆĶ”üõ║żµŹó’╝īõ╣¤Õ░▒µś»Ķ»┤Ķ»źµĢ░ÕłŚÕĘ▓ń╗ŵÄÆÕ║ÅÕ«īµłÉŃĆé - **µ»öĶŠāµ¼ĪµĢ░**...
6. **ÕĀåµÄÆÕ║Å**’╝ÜÕł®ńö©ÕĀåĶ┐Öń¦ŹµĢ░µŹ«ń╗ōµ×ä’╝īÕ░åÕŠģµÄÆÕ║ÅńÜäÕ║ÅÕłŚµ×äķĆĀµłÉõĖĆõĖ¬Õż¦ķĪČÕĀå’╝łµł¢Õ░ÅķĪČÕĀå’╝ē’╝īńäČÕÉÄÕ░åÕĀåķĪČÕģāń┤ĀõĖĵ£½Õ░ŠÕģāń┤Āõ║żµŹó’╝īĶ░āµĢ┤Õē®õĖŗńÜäÕģāń┤ĀõĖ║µ¢░ńÜäÕĀå’╝īķćŹÕżŹµŁżĶ┐ćń©ŗŃĆé **õ║īŃĆüÕ«×ķ¬īĶ«ŠĶ«Ī** Õ«×ķ¬īõĖŁ’╝īõĮ┐ńö©C++Ķ»ŁĶ©Ćń╝¢ń©ŗÕ«×ńÄ░Ķ┐Öõ║øµÄÆÕ║Å...
Ķ«ĪµĢ░µÄÆÕ║ÅõĖŹµś»Õ¤║õ║ĵ»öĶŠāńÜäµÄÆÕ║Åń«Śµ│Ģ’╝īÕ«āķĆÜĶ┐ćń╗¤Ķ«Īµ»ÅõĖ¬Õģāń┤ĀÕć║ńÄ░ńÜäµ¼ĪµĢ░’╝īńäČÕÉĵĀ╣µŹ«Ķ«ĪµĢ░ń╗ōµ×£ńø┤µÄźńĪ«Õ«ÜÕģāń┤ĀńÜäµ£Ćń╗łõĮŹńĮ«ŃĆéķĆéńö©õ║ÄķØ×Ķ┤¤µĢ┤µĢ░µÄÆÕ║Å’╝īõĖöĶīāÕø┤õĖŹÕż¦ńÜäÕ£║µÖ»ŃĆé 9. **µĪȵÄÆÕ║Å(Bucket Sort)** µĪȵÄÆÕ║ÅÕ░åÕģāń┤ĀÕłåÕĖāÕł░µ£ēķÖɵĢ░ķćÅńÜä...
ÕåƵ│ĪµÄÆÕ║ŵś»µ£Ćń«ĆÕŹĢńÜäµÄÆÕ║Åń«Śµ│Ģõ╣ŗõĖĆ’╝īķĆÜĶ┐ćķćŹÕżŹķüŹÕÄåÕŠģµÄÆÕ║ÅńÜäµĢ░ÕłŚ’╝īµ»öĶŠāńøĖķé╗Õģāń┤ĀÕ╣ȵĀ╣µŹ«ķ£ĆĶ”üõ║żµŹóõĮŹńĮ«µØźÕ«×ńÄ░µÄÆÕ║ÅŃĆéĶŠāÕż¦ńÜäÕģāń┤ĀķĆɵĖÉŌĆ£µĄ«ŌĆØÕł░µĢ░ÕłŚńÜäķĪČń½»’╝īÕ░▒Õāŵ░┤Õ║ĢõĖŗńÜäµ░öµ│ĪõĖŖÕŹćõĖƵĀĘŃĆéĶÖĮńäȵĢłńÄćĶŠāõĮÄ’╝īõĮåÕģČķĆ╗ĶŠæń«ĆÕŹĢ’╝īķĆéÕÉłµĢÖÕŁ”ÕÆī...
ÕÉłÕ╣ȵÄÆÕ║ŵś»õĖĆń¦ŹÕ¤║õ║ÄÕłåµ▓╗ńŁ¢ńĢźńÜäµÄÆÕ║Åń«Śµ│Ģ’╝īÕ«āÕ░åÕż¦ķŚ«ķóśÕłåĶ¦ŻõĖ║Õ░ÅķŚ«ķóśµØźĶ¦ŻÕå│ŃĆéķ”¢ÕģłÕ░åµĢ░ń╗äÕłåõĖ║õĖżõĖ¬ńøĖńŁēµł¢Ķ┐æõ╣ÄńøĖńŁēńÜäķā©Õłå’╝īńäČÕÉÄÕ»╣µ»ÅõĖĆķā©ÕłåķĆÆÕĮÆÕ£░Ķ┐øĶĪīµÄÆÕ║Å’╝īµ£ĆÕÉÄÕ░åń╗ōµ×£ÕÉłÕ╣ČŃĆéĶ┐Öń¦Źń«Śµ│ĢńÜ䵌ČķŚ┤ÕżŹµØéÕ║”õĖ║O(n log n)’╝īń©│Õ«ÜµĆ¦ÕźĮ’╝ī...
Õ«āķćŹÕżŹÕ£░ĶĄ░Ķ«┐Ķ┐ćĶ”üµÄÆÕ║ÅńÜäµĢ░ÕłŚ’╝īõĖƵ¼Īµ»öĶŠāõĖżõĖ¬Õģāń┤Ā’╝īÕ”éµ×£õ╗¢õ╗¼ńÜäķĪ║Õ║ÅķöÖĶ»»Õ░▒µŖŖõ╗¢õ╗¼õ║żµŹóĶ┐ćµØźŃĆéĶĄ░Ķ«┐µĢ░ÕłŚńÜäÕĘźõĮ£µś»ķćŹÕżŹÕ£░Ķ┐øĶĪīńø┤Õł░µ▓Īµ£ēÕåŹķ£ĆĶ”üõ║żµŹó’╝īõ╣¤Õ░▒µś»Ķ»┤Ķ»źµĢ░ÕłŚÕĘ▓ń╗ŵÄÆÕ║ÅÕ«īµłÉŃĆé **ń«Śµ│ĢµŁźķ¬ż**’╝Ü 1. µ»öĶŠāńøĖķé╗ńÜäÕģāń┤ĀŃĆéÕ”éµ×£ń¼¼õĖĆ...
ķĆēÕÅ¢õĖĆõĖ¬ŌĆ£Õ¤║ÕćåŌĆØÕģāń┤Ā’╝īÕ░åµĢ░ń╗äÕłåõĖ║õĖżķā©Õłå’╝ÜõĖĆķā©ÕłåµēƵ£ēÕģāń┤ĀķāĮÕ░Åõ║ÄÕ¤║Õćå’╝īÕÅ”õĖĆķā©ÕłåµēƵ£ēÕģāń┤ĀķāĮÕż¦õ║ÄÕ¤║Õćå’╝īńäČÕÉÄķĆÆÕĮÆÕ£░Õ»╣Ķ┐ÖõĖżķā©ÕłåĶ┐øĶĪīÕ┐½ķƤµÄÆÕ║ÅŃĆéÕ┐½ķƤµÄÆÕ║ÅńÜäÕ╣│ÕØ浌ČķŚ┤ÕżŹµØéÕ║”õĖ║O(n log n)’╝īµ£ĆÕØŵāģÕåĄõĖŗ’╝łÕĘ▓µÄÆÕ║ŵł¢ķĆåÕ║Å’╝ēõĖ║O(n^2)...
ķ”¢Õģłµ×äķĆĀõĖĆõĖ¬Õż¦ķĪČÕĀå’╝łµł¢Õ░ÅķĪČÕĀå’╝ē’╝īńäČÕÉÄÕ░åÕĀåķĪČÕģāń┤ĀõĖĵ£½Õ░ŠÕģāń┤Āõ║żµŹó’╝īµÄźńØĆÕ»╣Õē®õĮÖÕģāń┤Āķ揵¢░Ķ░āµĢ┤õĖ║ÕĀå’╝īķćŹÕżŹµŁżĶ┐ćń©ŗ’╝īńø┤Õł░µēƵ£ēÕģāń┤ĀķāĮĶó½µÄÆÕ║ÅŃĆé Ķ┐ÖõĖāń¦ŹµÄÆÕ║Åń«Śµ│ĢÕÉäµ£ēõ╝śń╝║ńé╣’╝īķĆéńö©Õ£║µÖ»õĖŹÕÉīŃĆéÕ┐½ķƤµÄÆÕ║ÅķĆÜÕĖĖµ£ĆÕ┐½’╝īõĮåµ£ĆÕØŵāģÕåĄõĖŗµĆ¦ĶāĮ...
Õ£©µ£ĆÕØÅńÜäµāģÕåĄõĖŗ’╝īÕåƵ│ĪµÄÆÕ║Åķ£ĆĶ”üĶ┐øĶĪīN(N-1)/2µ¼Īµ»öĶŠāÕÆīõ║żµŹó’╝īÕģȵŚČķŚ┤ÕżŹµØéÕ║”õĖ║O(N┬▓)ŃĆé 2. **ķ½śń║¦µÄÆÕ║Åń«Śµ│Ģ**’╝ÜĶ┐Öķā©ÕłåķĆÜÕĖĖµČēÕÅŖÕ”éÕ┐½ķƤµÄÆÕ║ŵł¢ÕĮÆÕ╣ȵÄÆÕ║ÅńŁēµø┤ķ½śµĢłńÜäń«Śµ│Ģ’╝īÕ«āõ╗¼ńÜ䵌ČķŚ┤ÕżŹµØéÕ║”õĖ║O(Log2(N))ŃĆéĶ┐Öõ║øń«Śµ│ĢÕł®ńö©Õłåµ▓╗ńŁ¢ńĢź...