
当
n为1至1000的整数时

的值
在數論中,對正整數n,歐拉函數 是小於或等於n的正整數中與n互質的數的數目。此函數以其首名研究者歐拉命名,它又稱為φ函數、歐拉商數等。
是小於或等於n的正整數中與n互質的數的數目。此函數以其首名研究者歐拉命名,它又稱為φ函數、歐拉商數等。
例如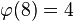 ,因為1,3,5,7均和8互質。
,因為1,3,5,7均和8互質。
欧拉函数实际上是模n的同余类所构成的乘法群(即环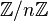 的所有单位元组成的乘法群)的阶。这个性质与拉格朗日定理一起構成了欧拉定理的證明。
的所有单位元组成的乘法群)的阶。这个性质与拉格朗日定理一起構成了欧拉定理的證明。
<script type="text/javascript"></script>
欧拉函數的值
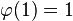 (小于等于1的正整数中唯一和1互質的數就是1本身)。
(小于等于1的正整数中唯一和1互質的數就是1本身)。
若n是質數p的k次冪, ,因為除了p的倍數外,其他數都跟n互質。
,因為除了p的倍數外,其他數都跟n互質。
歐拉函數是積性函數,即是说若m,n互質,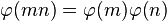 。證明:設A, B, C是跟m, n, mn互質的數的集,據中國剩餘定理,
。證明:設A, B, C是跟m, n, mn互質的數的集,據中國剩餘定理,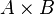 和C可建立雙射(一一對應)的關係。因此
和C可建立雙射(一一對應)的關係。因此 的值使用算術基本定理便知,
的值使用算術基本定理便知,
若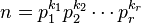 則
則 。
。
例如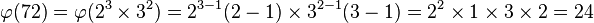
性质
n的欧拉函数 也是循环群 Cn 的生成元的个数(也是n阶分圆多项式的次数)。Cn 中每个元素都能生成 Cn 的一个子群,即必然是某个子群的生成元。而且按照定义,不同的子群不可能有相同的生成元。此外, Cn 的所有子群都具有 Cd 的形式,其中d整除n(记作d | n)。因此只要考察n的所有因数d,将 Cd 的生成元个数相加,就将得到 Cn 的元素总个数:n。也就是说:
也是循环群 Cn 的生成元的个数(也是n阶分圆多项式的次数)。Cn 中每个元素都能生成 Cn 的一个子群,即必然是某个子群的生成元。而且按照定义,不同的子群不可能有相同的生成元。此外, Cn 的所有子群都具有 Cd 的形式,其中d整除n(记作d | n)。因此只要考察n的所有因数d,将 Cd 的生成元个数相加,就将得到 Cn 的元素总个数:n。也就是说:
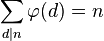
其中的d为n的正约数。
运用默比乌斯反转公式来“翻转”这个和,就可以得到另一个关于 的公式:
的公式:

其中 μ 是所谓的默比乌斯函数,定义在正整数上。
對任何兩個互質的正整數a, m(即 gcd(a,m) = 1),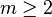 ,有
,有
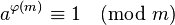
即欧拉定理。
这个定理可以由群论中的拉格朗日定理得出,因为任意与m互质的a都属于环 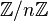 的单位元组成的乘法群
的单位元组成的乘法群
當m是質數p時,此式則為:
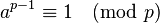
即費馬小定理。
生成函数
以下两个由欧拉函数生成的级数都是来自于上节所给出的性质: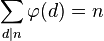 。
。
由 (n)生成的狄利克雷级数是:
(n)生成的狄利克雷级数是:
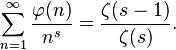
其中ζ(s)是黎曼ζ函数。推导过程如下:
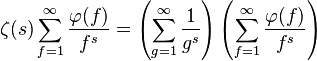
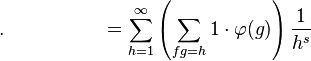
 使用开始时的等式,就得到:
使用开始时的等式,就得到: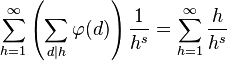 于是
于是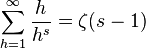
欧拉函数生成的朗贝级数如下:

其对于满足 |q|<1 的q收敛。
推导如下:
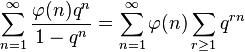
后者等价于:

欧拉函数的走势
随着n变大,估计 的值是一件很难的事。当n为质数时,
的值是一件很难的事。当n为质数时,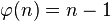 ,但有时
,但有时 又与n差得很远。
又与n差得很远。
在n足够大时,有估计:
对每个 ε > 0,都有n > N(ε)使得 
如果考虑比值:
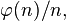
由以上已经提到的公式,可以得到其值等于类似1 − p − 1的项的乘积。因此,使比值小的n将是两两不同的质数的乘积。由素数定理可以知道,常数 ε 可以被替换为:
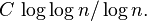
 就平均值的意义上来说是与n很相近的,因为:
就平均值的意义上来说是与n很相近的,因为:
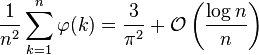
其中的O表示大O符号。这个等式也可以说明在集合 {1, 2, ..., n} 中随机选取两个数,则当n趋于无穷大时,它们互质的概率趋于 6 / π2 。一个相关的结果是比值 的平均值:
的平均值:
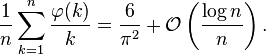
其他与欧拉函数有关的等式

-
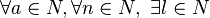 使得
使得 ![[(a >1 \and n > 1)\rightarrow (l|\varphi(a^n-1) \and l \geq n) ]](http://upload.wikimedia.org/math/e/d/6/ed66cfa3da48355a3b58c563c85f7ae1.png)
-
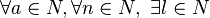 使得
使得 ![[(a >1 \and n > 6 \and 4 \not| n )\rightarrow (l|\varphi(a^n-1) \and l \geq 2n) ]](http://upload.wikimedia.org/math/f/f/c/ffce909d55a4ca5d26fb96dfbbec8c73.png)
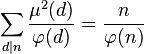
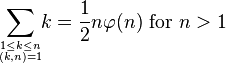

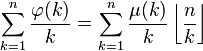


与欧拉函数有关的不等式
-
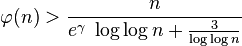 ,其中n > 2,γ 为欧拉-马歇罗尼常数。
,其中n > 2,γ 为欧拉-马歇罗尼常数。
-
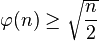 ,其中n > 0。
,其中n > 0。
- 对整数n > 6,
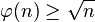 。
。
- 当n为质数时,显然有
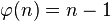 。对于合数的n,则有:
。对于合数的n,则有:
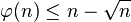
参考来源
- Milton Abramowitz、Irene A. Stegun, Handbook of Mathematical Functions, (1964) Dover Publications , New York. ISBN 0-486-61272-4. 24.3.2节.
- Eric Bach、Jeffrey Shallit, Algorithmic Number Theory, 卷 1, 1996, MIT Press. ISBN 0-262-02405-5, 8.8节,234页.
- 柯召,孙琦:数论讲义(上册),第二版,高等教育出版社,2001
分享到:








 的值
的值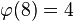 ,因為1,3,5,7均和8互質。
,因為1,3,5,7均和8互質。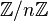
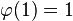 (小于等于1的正整数中唯一和1互質的數就是1本身)。
(小于等于1的正整数中唯一和1互質的數就是1本身)。 ,因為除了p的
,因為除了p的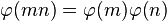 。證明:設A, B, C是跟m, n, mn互質的數的集,據
。證明:設A, B, C是跟m, n, mn互質的數的集,據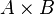 和
和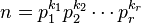
 。
。 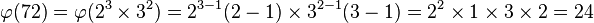
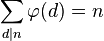

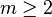 ,有
,有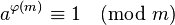

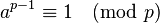
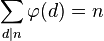 。
。 (n)生成的
(n)生成的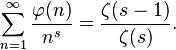
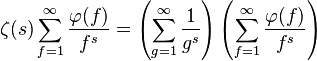
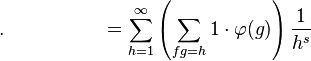

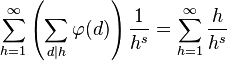
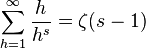

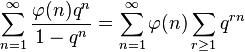

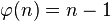 ,但有时
,但有时
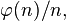
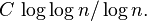
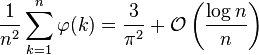
 的平均值:
的平均值: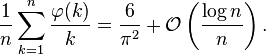

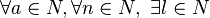 使得
使得 ![[(a >1 \and n > 1)\rightarrow (l|\varphi(a^n-1) \and l \geq n) ]](http://upload.wikimedia.org/math/e/d/6/ed66cfa3da48355a3b58c563c85f7ae1.png)
![[(a >1 \and n > 6 \and 4 \not| n )\rightarrow (l|\varphi(a^n-1) \and l \geq 2n) ]](http://upload.wikimedia.org/math/f/f/c/ffce909d55a4ca5d26fb96dfbbec8c73.png)
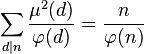
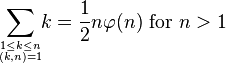

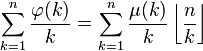


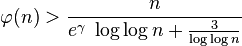 ,其中n > 2,γ 为
,其中n > 2,γ 为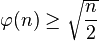 ,其中n > 0。
,其中n > 0。 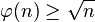 。
。 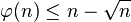



相关推荐
欧拉函数 C语言实现 #include "iostream" #include "math.h" #define maxsize 100 using namespace std; typedef struct node { int num; int total; }struct_num; struct_num a[maxsize]; int is_prime(int n)
欧拉函数 : 欧拉函数是数论中很重要的一个函数,欧拉函数是指:对于一个正整数 n ,小于 n 且和 n 互质的正整数(包括 1)的个数,记作 φ(n) 。 完全余数集合: 定义小于 n 且和 n 互质的数构成的集合为 Zn ,...
这里我们将详细探讨标题和描述中提到的几个关键概念:欧拉函数、Cayley定理、Mobius定理以及整数拆分。 1. **欧拉函数**(Euler's totient function): 欧拉函数φ(n)定义为小于n且与n互质的正整数的数量。它是...
欧拉函数(Euler's totient function),通常表示为φ(n),是数论中一个非常重要的函数。它定义为在1到n之间(包含1和n)与n互质的正整数个数。例如,φ(1)=1,因为只有1与1互质;φ(2)=1,因为只有1与2互质;φ(3)=...
标题提到的"代码实现,欧拉函数代码实现,matlab",表明我们将讨论如何在MATLAB环境中实现欧拉函数。欧拉函数,通常用φ(n)表示,是计算小于或等于n且与n互质的正整数的数量,它在数论中具有重要的地位。MATLAB是一种...
视频讲解欧拉定理和欧拉函数的证明。详细解释了证明简化剩余系的关系为什么要先证明完全剩余系的关系。以及欧拉函数的计算。
总的来说,"线性素筛 欧拉函数 区间筛素数.zip_sowoc_算法 欧拉函数 线性筛"这个压缩包文件包含了一种高效的算法实现,该算法能够在线性时间内筛选素数,并且能快速计算欧拉函数值,适用于需要处理大量素数和欧拉...
"欧拉函数和简化剩余系" 欧拉函数是数论中重要的函数之一,它描述了正整数中与互素的整数的个数。设n是一个正整数,欧拉函数φ(n)是指在1到n之间与n互素的整数的个数。 简化剩余系是指模m下的简化剩余类的集合。...
欧拉函数,通常用大写字母 φ 表示,是数论中一个非常重要的概念,由瑞士数学家欧拉在18世纪引入。这个函数在数论领域内有着广泛的应用,尤其是在模运算、同余类以及素数分布等方面。欧拉函数定义为:对于正整数n,...
在计算机科学和数学中,特别是在密码学和数论领域,扩展欧几里得算法、模幂运算以及欧拉函数是至关重要的工具。这些概念在解决复杂数学问题时起着核心作用,尤其是在处理整数的性质和计算上。下面我们将深入探讨这三...
在微积分中,\(e^x\) 的导数就是它自身,这使得欧拉函数在微分方程中具有特别的地位。然而,在这个上下文中,"欧拉"更可能指的是欧拉迭代法,而不是欧拉函数。 **euler.slx文件** 根据提供的文件名 "euler.slx",...
"hdu 1695 GCD(欧拉函数+容斥原理)" 题目大意是:给定 a, b, c, d, k,找到一队 x, y,满足 g(x, y) = k,且 x ∈ [1, b], y ∈ [1, d],问有多少对符合要求的 (x, y)。 思路是:gcd(x, y) == k 解释 x, y 都能...
欧拉函数,通常表示为φ(n),是数论中的一个重要概念,由数学家欧拉引入。这个函数计算了小于或等于n的正整数中与n互质(最大公约数为1)的数的数量。在密码学、计算复杂性和其他数学分支中,欧拉函数有广泛的应用。...
"欧拉函数 1" 欧拉函数是一种_IMPORTANT_函数在数论中,它表示 1 到 n-1 之间,与 n 互质的数的个数。在本篇文章中,我们将详细介绍欧拉函数的定义、计算方法和应用场景。 定义 欧拉函数 phi(n) 是指 1 到 n-1 ...
《简化剩余系与欧拉函数》的学习教案涵盖了数学领域中重要的数论概念,特别是与整数模运算相关的理论。欧拉函数(Euler's totient function),记为φ(k),是一个计算与给定正整数k互素的整数数量的函数。例如,φ(2...
**欧拉函数的基本概念** 欧拉函数,记作(),是数论中的一个重要函数,它表示小于或等于的正整数中与互素的数的个数。换句话说,()计算的是集合{0, 1, ..., - 1}中与的最大公约数为1的元素数量。这个函数在数论的...
欧拉函数的定义是:对于任意正整数n,欧拉函数φ(n)表示的是小于或等于n的正整数中与n互质的数的数目。所谓“互质”,指的是两个数的最大公约数为1。例如,φ(10)=4,因为1、3、7、9这四个数都和10互质。 在PHP中...
总结来说,"欧拉函数前缀"是一个在数学和计算机科学中涉及数论和算法的重要概念,它涉及到欧拉函数的性质、计算以及在实际编程问题中的应用。理解和掌握这一知识点,不仅有助于解决竞赛编程问题,还能为深入学习数论...
利用容斥原理对欧拉函数进行了推广,得出如下结论:1 )给出了欧拉函数的3 种初步推广,即函数φr;k (m),Ωr;k;l (m),Hr;k;l (m),找到并证明了r= 0 的 3 个表达式;2 )进一步推广了欧拉函数,得到并...
《Not矩阵的广义平方根及其在隐逻辑算子揭示和全矩阵圆欧拉函数定义中的应用》 本文深入探讨了Not矩阵的广义平方根的概念,并将其应用于逻辑操作的矩阵表示以及全矩阵圆欧拉函数的定义。Not矩阵在量子计算理论中...