- µÁÅÞºê: 98875 µ¼í
- µÇºÕê½:

- µØÑÞç¬: Õ«üÕ¥À
-

µûçþ½áÕêåþ▒╗
þñ¥Õî║þëêÕØù
- µêæþÜäÞÁäÞ«» ( 0)
- µêæþÜäÞ«║ÕØø ( 2)
- µêæþÜäÚù«þ¡ö ( 0)
Õ¡ÿµíúÕêåþ▒╗
- 2009-09 ( 3)
- 2009-08 ( 56)
- 2009-06 ( 1)
- µø┤ÕñÜÕ¡ÿµíú...
µ£Çµû░Þ»äÞ«║
-
oudoud´╝Ü
ÚØ×Õ©©õ©ìÚöÖ´╝îµ▓íÞºüµöÂÞùŵîëÚÆ«
240ÕñÜõ©¬jQueryµÅÆõ╗ -
idning´╝Ü
ding
þöƒµùѵéûÞ«║ -
javaõ╣ﵩ┤µ£ø´╝Ü
<%@ page contentType="& ...
Õ░åþ¢æÚíÁµò░µì«Õ»╝Õç║Õê░Excel(õ╗ѵ£Çþ«ÇÕìòþÜäµû╣Õ╝ÅÕæêþÄ░) -
zhoujiabin810812´╝Ü
þ«Çõ╗ïµÿÄõ║å´╝ü
Ú╗æÞÄô(BlackBerry)µÿ»õ╗Çõ╣ê -
WiseNeuron´╝Ü
Þ░óÞ░óÒÇéµáçÞ«░õ©Çõ©ï
240ÕñÜõ©¬jQueryµÅÆõ╗Â
þöƒµùѵéûÞ«║µÿ»µîç´╝îÕªéµ×£õ©Çõ©¬µê┐Úù┤Þúíµ£ë23õ©¬µêû23õ©¬õ╗Ñõ©èþÜäõ║║´╝îÚéúõ╣êÞç│Õ░æµ£ëõ©ñõ©¬õ║║þÜäþöƒµùÑþø©ÕÉîþÜ䵪éþÄçÞªüÕñºõ║Ä50%ÒÇéÞ┐ÖÕ░▒µäÅÕæ│þØÇÕ£¿õ©Çõ©¬Õà©Õ×ïþÜäµáçÕçåÕ░ÅÕ¡ªþÅ¡þ║º(30õ║║)õ©¡´╝îÕ¡ÿÕ£¿õ©ñõ║║þöƒµùÑþø©ÕÉîþÜäÕÅ»Þ⢵Ǻµø┤Ú½ÿÒÇéÕ»╣õ║Ä60µêûÞÇàµø┤ÕñÜþÜäõ║║´╝îÞ┐ÖþºìµªéþÄçÞªüÕñºõ║Ä99%ÒÇéõ╗ÄÕ╝òÞÁÀÚÇ╗Þ¥æþƒøþø¥þÜäÞºÆÕ║ªµØÑÞ»┤þöƒµùѵéûÞ«║Õ╣Âõ©ìµÿ»õ©ÇþºìµéûÞ«║´╝îõ╗ÄÞ┐Öõ©¬µò░Õ¡ªõ║ïÕ«×õ©Äõ©ÇÞê¼þø┤Þºëþø©µèÁÞºªþÜäµäÅõ╣ëõ©è´╝îÕ«âµëìþº░Õ¥ùõ©èµÿ»õ©Çõ©¬µéûÞ«║ÒÇéÕñºÕñܵò░õ║║õ╝ÜÞ«ñõ©║´╝î23õ║║õ©¡µ£ë2õ║║þöƒµùÑþø©ÕÉîþÜ䵪éþÄçÕ║öÞ»ÑÞ┐£Þ┐£Õ░Åõ║Ä50%ÒÇéÞ«íþ«ùõ©Äµ¡ñþø©Õà│þÜ䵪éþÄçÞó½þº░õ©║þöƒµùÑÚù«Úóÿ´╝î Õ£¿Þ┐Öõ©¬Úù«Úóÿõ╣ïÕÉÄþÜäµò░Õ¡ªþÉåÞ«║ÕÀ▓Þó½þö¿õ║ÄÞ«¥Þ«íÞæùÕÉìþÜäÕ»åþáüµö╗Õç╗µû╣µ│ò´╝Üþöƒµùѵö╗Õç╗ÒÇé
 
þø«Õ¢ò |
<script type="text/javascript"></script>
 
Õ»╣µ¡ñµéûÞ«║þÜäÞºúÚçè
þÉåÞºúþöƒµùѵéûÞ«║þÜäÕà│Úö«Õ£¿õ║ÄÚóåõ╝Üþø©ÕÉîþöƒµùÑþÜäµÉ¡ÚàìÕÅ»õ╗ѵÿ»þø©Õ¢ôÕñÜþÜäÒÇéÕªéÕ£¿ÕëìÚØóµëǵÅÉÕê░þÜäõ¥ïÕ¡É´╝î23õ©¬õ║║ÕÅ»õ╗Ñõ║ºþöƒC(23,2)= 23 ├ù 22/2 = 253 þºìõ©ìÕÉîþÜäµÉ¡Úàì´╝îÞÇîÞ┐Öµ»Åõ©ÇþºìµÉ¡ÚàìÚ⢵£ëµêÉÕèƒþø©þ¡ëþÜäÕÅ»Þâ¢ÒÇéõ╗ÄÞ┐ÖµáÀþÜäÞºÆÕ║ªþ£ï´╝îÕ£¿253þºìµÉ¡Úàìõ©¡õ║ºþöƒõ©ÇÕ»╣µêÉÕèƒþÜäÚàìÕ»╣õ╣ƒÕ╣Âõ©ìµÿ»ÚéúµáÀþÜäõ©ìÕÅ»µÇØÞ««ÒÇé
µìóõ©Çõ©¬ÞºÆÕ║ª´╝îÕªéµ×£õ¢áÞ┐øÕàÑõ║åõ©Çõ©¬µ£ëþØÇ22õ©¬õ║║þÜäµê┐Úù┤´╝îµê┐Úù┤ÞúíþÜäõ║║õ©¡õ╝ÜÕÆîõ¢áµ£ëþø©ÕÉîþöƒµùÑþÜ䵪éþÄçõ¥┐õ©ìµÿ»50´╝Ü50õ║å´╝îÞÇîµÿ»ÕÅÿÕ¥ùÚØ×Õ©©õ¢ÄÒÇéÕăÕøáµÿ»Þ┐ÖµùÂÕÇÖÕŬÞâ¢õ║ºþöƒ22þºìõ©ìÕÉîþÜäµÉ¡ÚàìÒÇéþöƒµùÑÚù«ÚóÿÕ«×ÚÖàõ©èµÿ»Õ£¿Úù«õ╗╗õ¢ò23õ©¬õ║║õ©¡õ╝ܵ£ëõ©ñõ║║þöƒµùÑþø©ÕÉîþÜ䵪éþÄçµÿ»ÕñÜÕ░æÒÇé
µªéþÄçõ╝░Þ«í
ÕüçÞ¿¡µ£ë n ÕÇïõ║║Õ£¿ÕÉîõ©Çµê┐ÚûôÕິ╝îÕªéµ×£ÞªüÞ¿êþ«ùµ£ëÕà®ÕÇïõ║║Õ£¿ÕÉîõ©ÇµùÑÕç║þöƒþÜäµ®ƒþÄç´╝îÕ£¿õ©ìÞÇâµà«þë╣µ«èÕøáþ┤áþÜäÕëìµÅÉõ©ï´╝îõ¥ïÕªéÚûÅÕ╣┤ÒÇüÚøÖÞâ×ÞâÄ´╝îÕüçÞ¿¡õ©ÇÕ╣┤365µùÑÕç║þöƒµªéþÄçµÿ»Õ╣│ÕØçÕêåõ¢êþÜä´╝êþÅ¥Õ»ªþöƒµ┤╗õ©¡´╝îÕç║þöƒµ®ƒþÄçõ©ìµÿ»Õ╣│ÕØçÕêåõ¢êþÜä´╝ëÒÇé
Þ¿êþ«ùµ®ƒþÄçþÜäµû╣µ│òµÿ»´╝îÚªûÕàêµë¥Õç║p(n)Þí¿þñ║ n ÕÇïõ║║õ©¡´╝îµ»ÅÕÇïõ║║þÜäþöƒµùѵùѵ£ƒÚâ¢õ©ìÕÉîþÜ䵪éþÄçÒÇéÕüçÕªén > 365´╝îµá╣µôÜÚ┤┐ÕÀóÕăþÉåÕ൪éþÄçþé║0´╝îÕüçÞ«¥ n Ôëñ 365´╝îÕêÖµªéþÄçõ©║
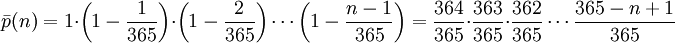
Õøáõ©║þ¼¼õ║îõ©¬õ║║õ©ìÞâ¢ÞÀƒþ¼¼õ©Çõ©¬õ║║µ£ëþø©ÕÉîþÜäþöƒµùÑ(µªéþÄçµÿ»364/365), þ¼¼õ©ëõ©¬õ║║õ©ìÞâ¢ÞÀƒÕëìõ©ñõ©¬õ║║þöƒµùÑþø©ÕÉî(µªéþÄçõ©║363/365),õ¥Øµ¡ñþ▒╗µÄ¿ÒÇéþö¿ÚÿÂõ╣ÿÕÅ»õ╗ÑÕåÖµêÉÕªéõ©ïÕ¢óÕ╝Å

p(n)Þí¿þñ║ nõ©¬õ║║õ©¡Þç│Õ░æ2õ║║þöƒµùÑþø©ÕÉîþÜ䵪éþÄç

nÔëñ365´╝îµá╣µì«Ú©¢ÕÀóÕăþÉå´╝î nÕñºõ║Ä365µùµªéþÄçõ©║1ÒÇé
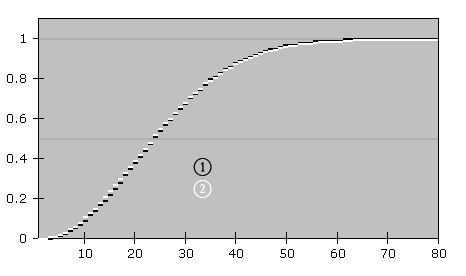
Õ¢ô n=23ÕÅæþöƒþÜ䵪éþÄçÕñºþ║ªµÿ»0.507ÒÇéÕàÂõ╗ûµò░Õ¡ùþÜ䵪éþÄçþö¿õ©èÚØóþÜäþ«ùµ│òÕÅ»õ╗ÑÞ┐æõ╝╝þÜäÕ¥ùÕç║µØÑ´╝Ü
 
| 10 | 12% |
| 20 | 41% |
| 30 | 70% |
| 50 | 97% |
| 100 | 99.99996% |
| 200 | 99.9999999999999999999999999998% |
| 300 | 1 ÔêÆ (7 ├ù 10ÔêÆ73) |
| 350 | 1 ÔêÆ (3 ├ù 10ÔêÆ131) |
| 366 | 100% |
 
µ│¿µäŵëǵ£ëõ║║Ú⢵ÿ»ÚÜŵ£║ÚÇëÕç║þÜä:õ¢£õ©║Õ»╣µ»ö,q(n)Þí¿þñ║µê┐Úù┤õ©¡ nõ©¬ÕàÂõ╗ûõ║║õ©¡õ©Äþë╣Õ«Üõ║║´╝êµ»öÕªéõ¢á´╝ëµ£ëþø©ÕÉîþöƒµùÑþÜ䵪éþÄç´╝Ü

Õ¢ôn = 22µùµªéþÄçÕŬµ£ëÕñºþ║ª0.059,þ║ªÚ½ÿõ║ÄÕìüõ©âÕêåõ╣ïõ©ÇÒÇéÕªéµ×£nõ©¬õ║║õ©¡µ£ë50´╝൪éþÄçÕ¡ÿÕ£¿µƒÉõ║║ÞÀƒõ¢áµ£ëþø©ÕÉîþöƒµùÑ´╝î nÞç│Õ░æÞªüÞ¥¥Õê░253 ÒÇéµ│¿µäÅÞ┐Öõ©¬µò░Õ¡ùÕñºÕñºÚ½ÿõ║Ä365/2 = 182.5: þ®ÂÕàÂÕăÕøáµÿ»Õøáõ©║µê┐Úù┤ÕåàÕÅ»Þ⢵£ëõ║øõ║║þöƒµùÑþø©ÕÉîÒÇé
µò░Õ¡ªÞ«║Þ»ü(ÚØ×µò░Õ¡ùµû╣µ│ò)
Õ£¿ Paul Halmos þÜäÞç¬õ╝áõ©¡´╝îõ╗ûÞ«ñõ©║þöƒµùѵéûÞ«║õ╗àÚÇÜÞ┐çµò░ÕÇ╝õ©èþÜäÞ«íþ«ùµØÑÞºúÚçèµÿ»õ©Çþºìµé▓ÕôÇÒÇéõ©║µ¡ñ´╝îPaul Halmosþ╗ÖÕç║õ║åõ©ÇþºìµªéÕ┐Áµò░Õ¡ªµû╣µ│òþÜäÞºúÚçè´╝îõ©ïÚØóÕ░▒µÿ»Þ┐Öþºìµû╣µ│ò´╝êÕ░¢þ«íÞ┐Öõ©¬µû╣µ│òÕîàÕɽõ©ÇÕ«ÜþÜäÞ»»ÕÀ«´╝ëÒÇé õ╣ÿþº»
 }-
}- þ¡ëõ║Ä 1´╝ìp(n), Õøᵡñµêæõ╗¼Õà│µ│¿þ¼¼õ©Çõ©¬n´╝îõ¢┐Õ¥ùõ╣ÿþº»Õ░Åõ║Ä1/2´╝îÞ┐ÖµáÀµêæõ╗¼Õ¥ùÕê░
![\sqrt[n-1]{\prod_{k=1}^{n-1}\left(1-{k \over 365}\right)}
<{1 \over n-1}\sum_{k=1}^{n-1}\left(1-{k \over 365}\right)](http://upload.wikimedia.org/math/3/b/2/3b292143b2a05a91f95e6e2ad86d5769.png) }-
}- þö▒Õ╣│ÕØçµò░õ©ìþ¡ëÕ╝ÅÕ¥ù´╝Ü

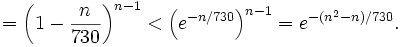 }-
}- (µêæõ╗¼ÚªûÕàêÕê®þö¿ÕÀ▓þƒÑþÜä1Õê░n´╝ì1µëǵ£ëµò┤µò░ÕÆîþ¡ëõ║Ä n(n´╝ì1)/2, þäÂÕÉÄÕê®þö¿õ©ìþ¡ëÕ╝Åõ©ìþ¡ëÕ╝Å 1´╝ìx┬á<┬áeÔêÆx.) Õªéµ×£õ╗àÕ¢ô

µ£ÇÕÉÄõ©Çõ©¬Þí¿Þ¥¥Õ╝ÅþÜäÕÇ╝õ╝ÜÕ░Åõ║Ä0.5ÒÇé ÕàÂõ©¡"loge"Þí¿þñ║Þç¬þäÂÕ»╣µò░ÒÇéÞ┐Öõ©¬µò░þòÑÕ¥«Õ░Åõ║Ä506´╝îÞ┐ɵ░öþ¿ìÕ¥«ÕÑ¢õ©Çþé╣þé╣Õ░▒ÕÅ»õ╗ÑÞ¥¥Õê░506´╝îþ¡ëõ║Än2´╝ìn´╝îµêæõ╗¼Õ░▒Õ¥ùÕê░n´╝Ø23ÒÇé
Õ£¿µÄ¿Õ»╝õ©¡´╝îHalmosÕåÖÚüô:
Þ┐Öõ©¬µÄ¿Õ»╝µÿ»Õƒ║õ║Äõ©Çõ║øµò░Õ¡ªþ│╗Õ¡ªþöƒÕ┐àÚí╗µÄîµÅíþÜäÚçìÞªüÕÀÑÕàÀÒÇéþöƒµùÑÚù«Úóÿµø¥þ╗ŵÿ»õ©Çõ©¬þ╗ØÕªÖþÜäõ¥ïÕ¡É´╝îþö¿µØѵ╝öþñ║þ║»µÇØþ╗┤µÿ»Õªéõ¢òÞâ£Þ┐çµ£║µó░Þ«íþ«ù´╝Üõ©Çõ©ñÕêåÚƃÕ░▒ÕÅ»õ╗ÑÕåÖÕç║Þ┐Öõ║øõ©ìþ¡ëÕ╝Å´╝îÞÇîõ╣ÿµ│òÞ┐Éþ«ùÕêÖÚ£ÇÞªüµø┤ÕñܵùÂÚù┤´╝îÕ╣µø┤µÿôÕç║ÚöÖ´╝îµùáÞ«║õ¢┐þö¿þÜäÕÀÑÕàÀµÿ»õ©ÇÕŬÚôàþ¼öÞ┐ÿµÿ»õ©ÇÕÅ░ÞÇüÕ╝ÅþöÁÞäæÒÇéÞ«íþ«ùÕÖ¿õ©ìÞ⢵ÅÉõ¥øþÜäµÿ»þÉåÞºúÕèø´╝îµêûµò░Õ¡ªµëìÞ⢴╝îµêûõ║ºþöƒµø┤Ú½ÿþ║ºÒÇüµÖ«ÚÇéÕîûþÉåÞ«║þÜäÕØÜÕ«×Õƒ║þíÇÒÇé[1]ÒÇé
þäÂÞÇîHalmosþÜäµÄ¿Õ»╝ÕŬµÿ¥þñ║Þç│Õ░æÚ£ÇÞªü23õ║║õ┐ØÞ»üÕ╣│þ¡ëµ£║õ╝Üõ©ïþÜäþöƒµùÑÕî╣Úàì´╝øÕøáõ©║µêæõ╗¼õ©ìþƒÑÚüôþ╗ÖÕç║þÜäõ©ìþ¡ëÕ╝ŵ£ëÕñܵ©àµÖ░´╝îÕøᵡñn´╝Ø22Þâ¢Õñƒµ¡úÕêçþÜäÕÅ»Þâ¢õ╣ƒµùáµ│òþí«Õ«ÜÒÇé
µ│øÕîûÕÆîÚÇ╝Þ┐æ
þöƒµùѵéûÞ«║ÕÅ»õ╗ѵĿÕ╣┐õ©Çõ©ï´╝ÜÕüçÞ«¥µ£ën õ©¬,µ»Åõ©Çõ©¬õ║║Úâ¢ÚÜŵ£║Õ£░õ╗Ä1ÕÆîþë╣Õ«ÜþÜäNõ©¬µò░õ©¡ÚÇëµï®Õç║µØÑõ©Çõ©¬µò░(NÕÅ»Þ⢵ÿ»365µêûÞÇàÕàÂõ╗ûþÜäÕñºõ║Ä0þÜäµò┤µò░)ÒÇé
p(n)Þí¿þñ║µ£ëõ©ñõ©¬õ║║ÚÇëµï®õ║åÕÉîµáÀþÜäµò░Õ¡ù´╝îÞ┐Öõ©¬µªéþÄçµ£ëÕñÜÕñº?
õ©ïÚØóþÜäÚÇ╝Þ┐æÕà¼Õ╝ÅÕÅ»õ╗ÑÕø×þ¡öÞ┐Öõ©¬Úù«Úóÿ

┬áN´╝Ø365þÜäþ╗ôµ×£
µ│øÕîû
õ©ïÚØóµêæõ╗¼µ│øÕîûþöƒµùÑÚù«Úóÿ: þ╗ÖÕ«Üõ╗Äþ¼ªÕÉêþª╗µòúÕØçÕîÇÕêåÕ©âþÜäÕî║Úù┤[1,d]ÚÜŵ£║ÕÅûÕç║nõ©¬µò┤µò░, Þç│Õ░æ2õ©¬µò░Õ¡ùþø©ÕÉîþÜ䵪éþÄçp(n;d) µ£ëÕñÜÕñº?
þ▒╗õ╝╝þÜäþ╗ôµ×£ÕÅ»õ╗ѵá╣µì«õ©èÚØóþÜäµÄ¿Õ»╝Õ¥ùÕç║ÒÇé
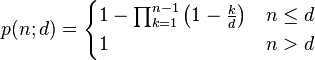


 }-
}- ÕÅìþ«ùÚù«Úóÿ
ÕÅìþ«ùÚù«ÚóÿÕÅ»Þ⢵ÿ»:
Õ»╣Þ┐Öõ©¬Úù«Úóÿµ£ëÕªéõ©ïÚÇ╝Þ┐æÕà¼Õ╝Å:
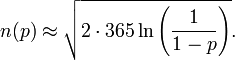
õ©¥õ¥ï
 
| ÚÇ╝Þ┐æ | õ╝░Þ«íN┬á:=365 | |||||
| p | n µÄ¿Õ╣┐ | n <N┬á:=365 | nÔåô | p(nÔåô) | nÔåæ | p(nÔåæ) |
|
0.01
|
0.14178 N |
2.70864
|
2 | 0.00274 | 3 |
0.00820
|
| 0.05 | 0.32029 N | 6.11916 | 6 | 0.04046 | 7 | 0.05624 |
|
0.1
|
0.45904 N |
8.77002
|
8 | 0.07434 | 9 |
0.09462
|
|
0.2
|
0.66805 N |
12.76302
|
12 | 0.16702 | 13 |
0.19441
|
| 0.3 | 0.84460 N | 16.13607 | 16 | 0.28360 | 17 | 0.31501 |
| 0.5 | 1.17741 N | 22.49439 | 22 | 0.47570 | 23 | 0.50730 |
| 0.7 | 1.55176 N | 29.64625 | 29 | 0.68097 | 30 | 0.70632 |
| 0.8 | 1.79412 N | 34.27666 | 34 | 0.79532 | 35 | 0.81438 |
| 0.9 | 2.14597 N | 40.99862 | 40 | 0.89123 | 41 | 0.90315 |
| 0.95 | 2.44775 N | 46.76414 | 46 | 0.94825 | 47 | 0.95477 |
|
0.99
|
3.03485 N |
57.98081
|
57 |
0.99012
|
58 | 0.99166 |
 
µ│¿µäÅ:µƒÉõ║øÕÇ╝Þó½þØÇÞë▓´╝îÞ»┤µÿÄÚÇ╝Þ┐æ õ©ì µÇ╗µÿ»µ¡úþí«ÒÇé
þ╗ÅÚ¬îµÇºµÁïÞ»ò
þöƒµùѵéûÞ«║ÕÅ»õ╗Ñþö¿Þ«íþ«ùµ£║õ╗úþáüþ╗ÅÚ¬îµÇºµ¿íµïƒ
days := 365; numPeople := 1; prob := 0.0; while prob < 0.5 begin numPeople := numPeople + 1; prob := 1 - ((1-prob) * (days-(numPeople-1)) / days); print "Number of people: " + numPeople; print "Prob. of same birthday: " + prob; end;
Õ║öþö¿
þöƒµùѵéûÞ«║µÖ«ÚüìþÜäÕ║öþö¿õ║ĵúǵÁïÕôêÕ©îÕ碵ò░:N-õ¢ìÚò┐Õ║ªþÜäÕôêÕ©îÞí¿ÕÅ»Þâ¢ÕÅæþöƒþó░µÆ×µÁïÞ»òµ¼íµò░õ©ìµÿ»2Nµ¼íÞÇîµÿ»ÕŬµ£ë2N/2µ¼íÒÇéÞ┐Öõ©Çþ╗ôÞ«║Þó½Õ║öþö¿Õê░þá┤ÞºúÕ»åþáüÕ¡ªµòúÕêùÕ碵ò░þÜäþöƒµùѵö╗Õç╗õ©¡ÒÇé
þöƒµùÑÚù«ÚóÿµëÇÚÜÉÕɽþÜäþÉåÞ«║ÕÀ▓þ╗ÅÕ£¿[Schnabel 1938]ÕÉìÕ¡ùÕŽÕüÜcapture-recaptureþÜäþ╗ƒÞ«íÞ»òÚ¬îÕ¥ùÕê░Õ║öþö¿´╝îµØÑõ╝░Þ«íµ╣ûÚçîÚ▒╝þÜäµò░ÚçÅÒÇé
õ©ìÕ╣│ÞííµªéþÄç
Õ░▒ÕâÅõ©èÚØóµÅÉÕê░þÜä´╝îþ£ƒÕ«×õ©ûþòîþÜäõ║║ÕÅúÕç║þöƒµùѵ£ƒÕ╣Âõ©ìµÿ»Õ╣│ÕØçÕêåÕ©âþÜäÒÇéÞ┐ÖþºìÚØ×ÕØçÞííþöƒµùѵªéþÄçÚù«Úóÿõ╣ƒÕÀ▓þ╗ÅÞó½ÞºúÕå│ÒÇé[Klamkin 1967]
Þ┐æõ╝╝Õî╣Úàì
µ¡ñÚù«ÚóÿÕŪÕñûõ©Çõ©¬ÞîâÕîûÕ░▒µÿ»µ▒éÕ¥ùÞªüÕ£¿ÚÜŵ£║ÚÇëÕÅûÕñÜÕ░æõ║║õ©¡µëìÞ⢵ë¥Õê░2õ©¬õ║║þöƒµùÑþø©ÕÉî´╝îþø©ÕÀ«1Õñ®´╝î2Õñ®þ¡ëþÜ䵪éþÄçÕñºõ║Ä50´╝à ÒÇéÞ┐Öµÿ»õ©¬µø┤ÚÜ¥þÜäÚù«ÚóÿÚ£ÇÞªüþö¿Õê░Õ«╣µûÑÕăþÉåÒÇéþ╗ôµ×£(ÕüçÞ«¥þöƒµùÑõ¥ØþäµîëþàºÕ╣│ÕØçÕêåÕ©â)µ¡úÕâÅÕ£¿µáçÕçåþöƒµùÑÚù«Úóÿõ©¡ÚéúµáÀõ╗ñõ║║ÕÉâµâè:
 
| 0 |   23 |
| 1 |   14 |
| 2 |   11 |
| 3 |    9 |
| 4 |    8 |
| 5 |    7 |
| 7 |    6 |
 
ÕŬڣÇÞªüÚÜŵ£║µè¢ÕÅû6õ©¬õ║║´╝îµë¥Õê░õ©ñõ©¬õ║║þöƒµùÑþø©ÕÀ«õ©ÇÕæ¿õ╗ÑÕåàþÜ䵪éþÄçÕ░▒õ╝ÜÞÂàÞ┐ç50%ÒÇé
ÕÅéÞÇâ
- Zoe Emily Schnabel: "The estimation of the total fish population of a lake"´╝굃ɵ╣ûõ©¡Ú▒╝þ▒╗µÇ╗ÚçÅõ╝░Þ«í´╝ë, þ¥ÄÕø¢µò░Õ¡ªµ£êÕêè 45 (1938Õ╣┤), 348-352ÚíÁ
- M. Klamkin´╝îD. Newman: "Extensions of the birthday surprise"´╝êþöƒµùѵâèÕû£þÜäµë®Õàà´╝ë, Journal of Combinatorial Theory 3 (1967Õ╣┤),279-282ÚíÁÒÇé
- D. Blom: "a birthday problem"þöƒµùÑÚù«Úóÿ, þ¥ÄÕø¢µò░Õ¡ªµ£êÕêè 80 (1973Õ╣┤),1141-1142ÚíÁÒÇéÞ┐Öõ©ÇÞ«║µûçÞ»üµÿÄõ║åÕ¢ôþöƒµùѵîëþàºÕ╣│ÕØçÕêåÕ©â´╝îõ©ñõ©¬þöƒµùÑþø©ÕÉîþÜ䵪éþÄçµ£ÇÕ░ÅÒÇé
- 2009-08-11 00:45
- µÁÅÞºê 1867
- Þ»äÞ«║(1)
- µƒÑþ£ïµø┤ÕñÜ
ÕÅæÞí¿Þ»äÞ«║
-
õ¢áµâ│þƒÑÚüôµé¿þÜäÚéúõ©¬þ½»ÕÅúÕÅÀÞó½Úéúõ©¬þ¿ïÕ║ÅÕìáþö¿õ║åÕÉù´╝ƒ
2009-09-14 18:24 2578õ╗Ñõ©ïµûçþ½áõ©╗Þªüõ╗Ñ80þ½»ÕÅúÕÅÀõ©║õ¥ï´╝îÕªéµ×£µâ│þƒÑÚüôÕàÂõ╗ûþÜäþ½»ÕÅúÕÅÀõ╣ƒÕÅ»õ╗Ñõ¢┐þö¿ ... -
Õ£¿þöÁ޻صÄÑÕàѵùÂÕñäþÉåÚƒ│ÚóæµÆ¡µö¥
2009-08-11 00:56 1004ÚÇÜ޻صÿ»µëïµ£║µ£ÇÚçìÞªüþÜäÕèƒÞ⢴╝îµëïµ£║µØÑþöÁõ╝ܵèæÕ굡úÕ£¿Þ┐ÉÞíîþÜäMIDletÞ┐É ... -
ÕìòÕÉæÚÖÀÚù¿Õ碵ò░
2009-08-11 00:55 2761ÕìòÕÉæÚÖÀÚù¿Õ碵ò░(One-way Trapdoor Functio ... -
RSAÕèáÕ»åþ«ùµ│ò
2009-08-11 00:54 28581. Õ»åÚÆÑþÜäõ║ºþöƒÔæá ÚÇëõ©ñõ©¬ ... -
µò░µì«ÕèáÕ»åµáçÕçåDES
2009-08-11 00:54 1546µò░µì«ÕèáÕ»åµáçÕçåDES ÒÇÇÒÇǵò░µì«ÕèáÕ»åþ«ùµ│ò´╝êData Encryp ... -
JavaÕüÜõ©Çõ©¬µ£Çþ«ÇÕìòþÜäSocketÚÇÜÞ»Øþ¿ïÕ║Å
2009-08-11 00:53 1129Javaõ©¡þÜäþ¢æþ╗£þ╝ûþ¿ïµÿ»õ©Çõ©¬Õ¥êÚçìÞªüþÜäÚâ¿Õêå´╝îõ╣ƒµÿ»ÕàÂþ╝ûþ¿ïõ╝ÿÞÂèµÇºþÜäÕ£░µû╣ ... -
C/Sµ¿íÕ╝Åõ©¡þÜäÞ┐£þ¿ïµû╣µ│òÞ░âþö¿
2009-08-11 00:52 2123µæÿÞªü Õƒ║õ║ÄC/SÞ«¥Þ«íµ¿íÕ╝Å´╝î ... -
JavaÕèáÕ»åÕÆîµò░Õ¡ùþ¡¥ÕÉìþ╝ûþ¿ïÕ┐½ÚǃÕàÑÚù¿
2009-08-11 00:51 699ÒÇǵûç/jwsh1984 ÒÇÇÒÇǵ£¼µûçõ©╗ÞªüÞ░êõ©Çõ©ïÕ»åþáüÕ¡ªõ©¡þÜäÕèáÕ»åÕÆî ... -
VigenereÕ»åþáüõ©ÄPlayfairÕ»åþáü µöÂ
2009-08-11 00:50 4036þ╗┤ÕÉëÕ░╝õ║Ü(vigenere)Õ»åþáü,þ¥ÄÕø¢ÕìùÕîùµêÿõ║ëµ£ƒÚù┤ÞüöÕåøÕ╣┐µ│ø ... -
javaÕ«×þÄ░DESÕèáÕ»åþ«ùµ│ò
2009-08-11 00:49 2427õ©ÇÒÇüjavaÕ«×þÄ░DESÕèáÕ»åþ«ùµ│ò õ©║õ║åÕ«×þÄ░õ©ÇÕ»╣Õ»åÚÆÑÕ»╣µò┤õ©¬Úí╣þø«µëǵ£ë ... -
DESþ«ùµ│òþÉåÞ«║
2009-08-11 00:48 1440DESþ«ùµ│òþÉåÞ«║ µ£¼õ©ûþ║¬õ║öÕì ... -
µ¼ºµïëÕ碵ò░
2009-08-11 00:47 1645Õ¢ônõ©║1Þç│1000þÜäµò┤µò░µùÂþÜäÕÇ╝ ┬á ... -
µéûÞ«║µªéÕ┐Á
2009-08-11 00:47 837ÕàÂÕ«Üõ╣ëÕÅ»õ╗ÑÞ┐ÖµáÀÞí¿Þ┐░´╝Üþö▒õ©Çõ©¬Þó½µë┐Þ«ñµÿ»þ£ƒþÜäÕæ¢Úóÿõ©║ÕëìµÅÉ´╝îÞ«¥õ©║B´╝îÞ┐øÞíî ... -
TCP/IPþ½»ÕÅúÕƒ║þíÇÕ©©Þ»åÕñºÕà¿
2009-08-11 00:44 806þ½»ÕÅúÕÅ»Õêåõ©║3Õñºþ▒╗´╝Ü 1´╝ë Õà¼Þ«ñþ½»ÕÅú´╝êWell Known Po ... -
ÕÁîÕàÑÕ╝ÅÕñäþÉåÕÖ¿þÜäÕƒ║µ£¼µªéÕ┐Á
2009-08-11 00:42 1092ÕÁîÕàÑÕ╝Åþ│╗þ╗ƒþÜäµá©Õ┐âÚâ¿õ╗µÿ»ÕÉäþºìþ▒╗Õ×ïþÜäÕÁîÕàÑÕ╝ÅÕñäþÉåÕÖ¿´╝îþø«ÕëìÕà¿õ©ûþòîÕÁîÕàÑÕ╝Å ... -
ÕÁîÕàÑÕ╝ÅÕ«×µùµôìõ¢£þ│╗þ╗ƒþÜäþÄ░þèÂÕÆîµ£¬µØÑ
2009-08-11 00:42 1267ÕåàÕ«╣µæÿÞªü´╝Üõ╗ÄRTOS´╝êÕÁîÕàÑÕ╝ÅÕ«×µùµôìõ¢£þ│╗þ╗ƒ´╝ëÕÅæÕ▒òþÜäÕÄåÕÅ▓ÒÇüRTOS ... -
þ¢æþ╗£þ╝ûþ¿ï´╝ì´╝ìWININET
2009-08-11 00:40 1625┬á õ©Çõ©¬InternetÕ«óµêÀþ½»þ¿ïÕ║ÅþÜäþø«þÜäµÿ»ÚÇÜÞ┐çInterne ... -
ModÞ┐Éþ«ù
2009-08-11 00:37 1746µ¿ípÞ┐Éþ«ù þ╗ÖÕ«Üõ©Çõ©¬µ¡úµò┤µò░p´╝îõ╗╗µäÅõ©Çõ©¬µò┤µò░n´╝îõ©ÇÕ«ÜÕ¡ÿÕ£¿þ¡ëÕ╝Å ... -
µ¼ºµïëÕ«ÜþÉå (µò░Þ«║)
2009-08-11 00:36 1673Õ£¿µò░Þ«║õ©¡µ¼ºµïëÕ«ÜþÉå´╝êõ╣ƒþº░Þ┤╣Ú®¼-µ¼ºµïëÕ«ÜþÉåµêûµ¼ºµïëÕ碵ò░Õ«ÜþÉå: ÞïÑm,a ... -
µò░Õ¡ùþ¡¥ÕÉìÕÆîÕèáÕ»å
2009-08-11 00:36 3891ÕàÀõ¢ôµ¡ÑÚ¬ñÕªéõ©ïÒÇéAliceõ©ÄBobõ║ƵìóÕà¼ÚÆÑÒÇéAliceþö¿Þç¬ÕÀ▒þÜäþºü ...








þø©Õà│µÄ¿ÞìÉ
þöƒµùѵéûÞ«║µÿ»õ©Çõ©¬þ╗ÅÕà©þÜ䵪éþÄçÚù«Úóÿ´╝îÕ«âµîçÕç║Õ£¿õ©Çõ©¬µê┐Úù┤ÚçîÕŬުüµ£ë23õ║║´╝îÕ░▒Õ¡ÿÕ£¿Þç│Õ░æõ©ñõ║║µïѵ£ëþø©ÕÉîþöƒµùÑþÜ䵪éþÄçÞÂàÞ┐ç50%ÒÇéÞ┐Öõ©¬µéûÞ«║µÅ¡þñ║õ║åÕ░ŵªéþÄçõ║ïõ╗ÂÕ£¿ÕñºµáÀµ£¼õ©ïþÜäÕÅ»Þ⢵ǺÒÇéÚÇÜÞ┐çPythonþ╝ûþ¿ï´╝îµêæõ╗¼ÕÅ»õ╗ѵ¿íµïƒÞ┐Öõ©¬þÄ░Þ▒íµØÑÚ¬îÞ»üÞ┐Öõ©¬þÉåÞ«║ÒÇé ...
þöƒµùѵéûÞ«║´╝îõ╣ƒÞó½þº░õ©║þöƒµùÑÚù«Úóÿ´╝îµÿ»õ©Çõ©¬Õ£¿þ╗ƒÞ«íÕ¡ªõ©¡þ╗ÅÕ©©Þó½µÅÉÕÅèþÜ䵪éÕ┐Á´╝îÕ«âµÂëÕÅèÕê░Þ«íþ«ùÕ£¿õ©Çþ╗äÚÜŵ£║ÚÇëÕÅûþÜäõ║║õ©¡´╝îÞç│Õ░æµ£ëõ©ñõ║║µïѵ£ëþø©ÕÉîþöƒµùÑþÜ䵪éþÄçÒÇéÞ┐Öõ©¬µªéþÄçµ»öþø┤Þºëõ©èÞªüÚ½ÿÕ¥ùÕñÜ´╝îÚÇÜÕ©©Õ£¿23õ║║µù´╝îÞ┐Öõ©¬µªéþÄçÕ░▒ÕÀ▓þ╗ÅÞÂàÞ┐çõ║å50%ÒÇéÕ£¿MATLAB...
õ©Çõ©¬µê┐Úù┤µ£ë23õ©¬õ║║´╝îõ╝ܵ£ëõ©ñõ©¬õ║║þöƒµùÑþø©ÕÉîÕÉù´╝ƒþ¡öµíêµÿ»µ£ë50%þÜ䵪éþÄçÒÇéÞ┐ÖÕ░▒µÿ»µëÇÞ░ôþÜäþöƒµùÑÚù«Úóÿbirthday problem´╝ëµêûþöƒµùѵéûÞ«║´╝êbirthday paradox´╝ëÒÇéµ£¼µûçÕø×þ¡öþÜäÚù«Úóÿµÿ»´╝îÕ¢ôõ║║µò░õ╝ùÕñܵù´╝îþöƒµùÑþø©ÕÉîþÜ䵪éþÄçÞ¥¥Õê░50%´╝îµ£ëÕñÜÕ░æõ║║ÒÇé
ÕÅ»õ╗Ñ
þöƒµùѵéûÞ«║þÜäõ║ÆÕ迵╝öþñ║ Þªüµ▒é Ú£ÇÞªüµØÑÕ«ëÞúàõ¥ØÞÁûÚí╣Õ╣ÂÚÇÜÞ┐çnpmÞ┐ÉÞíîÞäܵ£¼ÒÇé ÕÅ»þö¿Õæ¢õ╗ñ Õæ¢õ╗ñ µÅÅÞ┐░ npm install Õ«ëÞúàÚí╣þø«õ¥ØÞÁûÚí╣ npm start µ×äÕ╗║Úí╣þø«Õ╣µëôÕ╝ÇÞ┐ÉÞíîWebµ£ìÕèíÕÖ¿þÜäÚí╣þø« npm run build õ¢┐þö¿þöƒõ║ºÞ«¥þ¢«´╝êµ£ÇÕ░ÅÕîû´╝îõ©æÕîûþ¡ë´╝ë...
õ╗ÄÕ╝òÞÁÀÚÇ╗Þ¥æþƒøþø¥þÜäÞºÆÕ║ªµØÑÞ»┤þöƒµùѵéûÞ«║Õ╣Âõ©ìµÿ»õ©ÇþºìµéûÞ«║´╝îõ╗ÄÞ┐Öõ©¬µò░Õ¡ªõ║ïÕ«×õ©Äõ©ÇÞê¼þø┤Þºëþø©µèÁÞºªþÜäµäÅõ╣ëõ©è´╝îÕ«âµëìþº░Õ¥ùõ©èµÿ»õ©Çõ©¬µéûÞ«║ÒÇéÕñºÕñܵò░õ║║õ╝ÜÞ«ñõ©║´╝î23õ║║õ©¡µ£ë2õ║║þöƒµùÑþø©ÕÉîþÜ䵪éþÄçÕ║öÞ»ÑÞ┐£Þ┐£Õ░Åõ║Ä50%ÒÇéÞ«íþ«ùõ©Äµ¡ñþø©Õà│þÜ䵪éþÄçÞó½þº░õ©║þöƒµùÑÚù«Úóÿ...
Þ┐Öõ©¬Õ«×õ¥ïµù¿Õ£¿Õ©«Õè®Õ╝ÇÕÅæÞÇàµÄîµÅíÕªéõ¢òÕ£¿VBþÄ»Õóâõ©¡Õ«×þÄ░Þ┐Öõ║øÕèƒÞ⢴╝îÕÉîµùÂþÉåÞºúþöƒµùѵéûÞ«║þÜäÕƒ║µ£¼µªéÕ┐ÁÒÇé þöƒµùѵéûÞ«║µÿ»õ©Çõ©¬µªéþÄçþÉåÞ«║´╝îÕ«âµîçÕç║Õ£¿õ©Çõ©¬µê┐Úù┤Úçî´╝îÕŬڣÇÞªüÕñºþ║ª23õ║║´╝îÕ░▒µ£ëÕÅ»Þ⢵£ëõ©ñõ©¬õ║║þÜäþöƒµùѵÿ»ÕÉîõ©ÇÕñ®ÒÇéÕ£¿VBõ©¡´╝îµêæõ╗¼ÕÅ»õ╗ѵ¿íµïƒÞ┐Öõ©¬...
Þ┐Öõ©¬Úù«Úóÿ´╝îõ╣ƒÞó½þº░õ©║ÔÇ£þöƒµùѵéûÞ«║ÔÇصêûÞÇàÔÇ£þöƒµùÑÚù«ÚóÿÔÇØÒÇéþ£ïõ╝╝þ«ÇÕìò´╝îÕì┤Õ¥ÇÕ¥ÇÞâ¢Õ╝òÕÅæõ║║õ╗¼Õ»╣µªéþÄçþø┤ÞºéþÉåÞºúþÜäþûæµâæÒÇéÞ┐ÖÚçîµêæõ╗¼Õ░åÞ»ªþ╗åµÄóÞ«¿Þ┐Öõ©¬Úù«Úóÿ´╝îÕ╣ÂÚÇÜÞ┐çÕ«×õ¥ïÞºúÚçèõ©║õ╗Çõ╣êÕ£¿õ©Çõ©¬50õ║║þÜäÕ®Üþñ╝õ©¡´╝îµ£ëõ©ñõ║║ÕÉîõ©ÇÕñ®þöƒµùÑþÜ䵪éþÄçÕ«×ÚÖàõ©èÚ½ÿÞ¥¥97%...
Þ┐Öõ©¬Úù«ÚóÿÚÇÜÕ©©Þó½þº░õ©║ÔÇ£þöƒµùѵéûÞ«║ÔÇØ´╝îÕøáõ©║þø┤Þºëõ©èõ║║õ╗¼Õ¥ÇÕ¥Çõ¢Äõ╝░õ║åÞ┐Öõ©¬µªéþÄçÒÇé þöƒµùѵéûÞ«║þÜäµá©Õ┐âµÿ»þÉåÞºúÕ£¿365Õñ®þÜäõ©ÇÕ╣┤õ©¡´╝îÕªéµ×£µ£ënõ©¬õ║║´╝îõ╗ûõ╗¼þöƒµùÑÚâ¢õ©ìþø©ÕÉîþÜ䵪éþÄçµÿ»Õªéõ¢òÚÜÅnÕÅÿÕîûþÜäÒÇéÚªûÕàê´╝îþ¼¼õ©Çõ©¬õ║║þÜäþöƒµùÑÕÅ»õ╗ѵÿ»õ╗╗õ¢òõ©ÇÕñ®´╝îµëÇõ╗Ñ...
3. **µªéþÄçÞ«íþ«ù**´╝ܵá╣µì«ÔÇ£þöƒµùѵéûÞ«║ÔÇØ´╝êõ╣ƒþº░õ©║ÔÇ£þöƒµùÑÚù«ÚóÿÔÇØ´╝ë´╝îÞ«íþ«ùÞç│Õ░æõ©ñõ©¬õ║║Õ£¿ÕÉîõ©Çþ╗äõ║║õ©¡þöƒµùÑþø©ÕÉîþÜ䵪éþÄçÒÇéþöƒµùѵéûÞ«║µîçÕç║´╝îÕ£¿õ©Çõ©¬µ£ë23õ║║õ╗Ñõ©èþÜäþ¥ñõ¢ôõ©¡´╝îµ£ëÞÂàÞ┐ç50%þÜ䵪éþÄçÕ¡ÿÕ£¿Þç│Õ░æõ©ñõ║║ÕÉîõ©ÇÕñ®þöƒµùÑÒÇé 4. **ÕŻ޺åÕîû**´╝ÜÕÅ»Þâ¢...
Õ£¿µ£¼Úí╣þø«"matlabÕ╝ÇÕÅæ-Birthdayprobabilitysolution"õ©¡´╝îµêæõ╗¼õ©╗ÞªüÕà│µ│¿þÜäµÿ»ÞæùÕÉìþÜäÔÇ£þöƒµùѵéûÞ«║ÔÇØÚù«Úóÿ´╝îÞ┐Öµÿ»õ©Çõ©¬µªéþÄçÞ«║þÜäþ╗ÅÕà©Úù«ÚóÿÒÇéÕ£¿Þ┐Öõ©¬Úù«Úóÿõ©¡´╝îµêæõ╗¼µÄóÞ«¿þÜäµÿ»Õ£¿õ©Çõ©¬µê┐Úù┤ÚçîÚ£ÇÞªüÕñÜÕ░æõ║║´╝îµëìÞâ¢õ¢┐Õ¥ùÞç│Õ░æµ£ëõ©ñõ©¬õ║║þÜäþöƒµùÑþø©ÕÉîþÜä...
Þ┐Öþºìµö╗Õç╗µû╣µ│òÕƒ║õ║ÄþöƒµùѵéûÞ«║´╝îÕì│Õ£¿ÕñºÚçÅÚÜŵ£║µò░µì«õ©¡Õ»╗µë¥ÚçìÕñìþÜäÕÅ»Þ⢵ǺÒÇé 2. Rhoµö╗Õç╗µÁïÞ»òÚÇÜÞ┐çÞ┐¢Þ©¬ÕÀ▓þ╗ÅÞ«íþ«ùÞ┐çþÜäµæÿÞªü´╝îÕ╣ÂÕ░ØÞ»òµë¥Õê░ÕàÀµ£ëþø©ÕÉîµ£ÇÚ½ÿõ¢ìþÜäµæÿÞªüþÜäµÂêµü»ÕÇ╝Õ»╣ÒÇéÞ┐Öþºìµö╗Õç╗µû╣µ│òµ»öþöƒµùѵö╗Õç╗µø┤ÕèáÚ½ÿµòê´╝îÕ░ñÕàµÿ»Õ£¿ÕñäþÉåÕñºÚçŵò░µì«µùÂ...
ÕàÂÕƒ║µ£¼ÕăþÉåµ║ÉÞç¬õ║Äõ©ÇþºìÕÀºÕªÖþÜäµÇصâ│ÔÇöÔÇöþöƒµùѵéûÞ«║´╝îÞ┐ÖþºìµÇصâ│ÕÉîµáÀÕÅ»Õ║öþö¿õ║ÄÕñÜþºìÕ£║µÖ»õ©¡ÒÇé 1980Õ╣┤´╝îRichard BrentÕ£¿ÕàÂÞ«║µûçõ©¡Õ»╣Pollard-Rhoþ«ùµ│òÞ┐øÞíîõ║åµö╣Þ┐ø\[2\]´╝îÞ┐øõ©Çµ¡ÑµÅÉÕìçõ║åÞ»Ñþ«ùµ│òþÜäµÇºÞâ¢ÒÇéÕªéõ╗è´╝îPollard's Rhoþ«ùµ│òÕÀ▓µêÉõ©║...
µá╣µì«þöƒµùѵéûÞ«║´╝îÕªéµ×£µ£ëÕñÜõ║Ä366õ©¬õ║║´╝îÚéúõ╣êÕ£¿ÚÜŵ£║ÚÇëµï®þÜäµâàÕåÁõ©ï´╝îÞç│Õ░æõ╝ܵ£ëõ©ñõ©¬õ║║Õ£¿ÕÉîõ©ÇÕñ®Þ┐çþöƒµùÑ´╝îÞ┐Öµÿ»Õøáõ©║ÞÇâÞÖæÕê░Úù░Õ╣┤ÕÅ»Þ⢵£ë366Õñ®ÒÇéÞ┐ÖÚçî367õ║║ÞÂàÞ┐çõ║åÞ┐Öõ©¬µò░Õ¡ù´╝îµëÇõ╗Ñõ©ÇÕ«Üõ╝ÜÕ¡ÿÕ£¿Þç│Õ░æõ©ÇÕ»╣ÕÉîõ©ÇÕñ®þöƒµùÑþÜäÕ¡ªþöƒÒÇé 3. õ©ìÕØçÕîÇÕêåÚàì...
ÚÇÜÞ┐çÕà¼Õ╝ÅÞ«íþ«ùÕÆíµïƒÞ«íþ«ùõ©ñþºìµû╣µ│ò´╝îþÉåÞºúÕ╣ÂÚ¬îÞ»üõ║åÔÇ£þöƒµùѵéûÞ«║ÔÇØþÜ䵪éÕ┐Á´╝îÕì│Õ£¿õ©Çõ©¬Õ░Åþ¥ñõ¢ôõ©¡µë¥Õê░Õà▒õ║½þöƒµùÑþÜ䵪éþÄçµ»öþø┤Þºëõ©èµø┤Ú½ÿÒÇé 2. **ÚÜŵ£║µ©©ÞÁ░µø▓þ║┐**´╝Üþ╗âõ╣á6_02µÂëÕÅèÕê░ÚÜŵ£║µò░þöƒµêÉÕÆîÚÜŵ£║µ©©ÞÁ░þÉåÞ«║´╝îÚÇÜÞ┐çÕ£¿µ»Åõ©¬ÚÜŵ£║Úù┤ÚÜöþé╣õ©èþöƒµêÉ...
Þ»¥õ╗ÂÕêùÕç║õ║åõ©Çþ│╗Õêùµùѵ£ƒ´╝îÕÅ»Þ⢵ÿ»õ©║õ║åÞ«¿Þ«║ÞæùÕÉìþÜäÔÇ£þöƒµùѵéûÞ«║ÔÇØ´╝îÕì│Õ£¿õ©Çõ©¬µê┐Úù┤Úçî´╝îÚ£ÇÞªüÕñÜÕ░æõ║║Õ£¿õ©ÇÞÁÀµëìµ£ëÕÅ»Þâ¢Þç│Õ░æµ£ëõ©ñõ©¬õ║║þöƒµùÑþø©ÕÉî´╝îÞ┐Öõ©¬µéûÞ«║Õ©«Õè®Õ¡ªþöƒþÉåÞºúµªéþÄçþÜäÕƒ║µ£¼µªéÕ┐ÁÕÆîÕ«×ÚÖàÕ║öþö¿ÒÇé ÕàÂõ╗ûþ½áÞèéÕªéÔÇ£ÕŬÞÁóõ©ìÞ¥ôþÜ䵩©µêÅÔÇØÒÇü...
þ¼¼õ║öÚâ¿ÕêåµÂëÕÅèþöƒµùѵéûÞ«║´╝îÞ┐Öµÿ»õ©Çõ©¬þ╗ÅÕà©þÜ䵪éþÄçÚù«ÚóÿÒÇéÕ£¿30õ║║þÜäþÅ¡þ║ºõ©¡´╝îÞç│Õ░æµ£ëõ©ñõ¢ìÕÉîÕ¡ªþöƒµùÑþø©ÕÉîþÜ䵪éþÄçÕÅ»õ╗ÑÚÇÜÞ┐çÞ«íþ«ùõ║ÆÞíÑõ║ïõ╗´╝êµëǵ£ëõ║║þöƒµùÑÚâ¢õ©ìþø©ÕÉî´╝ëþÜ䵪éþÄçµØÑÕ¥ùÕê░ÒÇéÕê®þö¿Ú©¢ÕÀóÕăþÉå´╝îÕÅ»õ╗ѵĿþ«ùÞç│Õ░æõ©ñõ║║ÕÉîµ£êþöƒµùÑþÜ䵪éþÄçÒÇé 6. ...
þø«Õ¢ò ┬À ┬À ┬À ┬À ┬À ┬À Õç║þëêÞÇàþÜäÞ»Ø õ©ôիµîçÕ»╝ÕºöÕæÿõ╝Ü Þ»æÞÇàÕ║Å ÕëìÞ¿Ç þ¼¼õ©ÇÚâ¿Õêå Õƒ║þíÇþƒÑÞ»å Õ╝òÞ¿Ç þ¼¼1þ½á þ«ùµ│òÕ£¿Þ«íþ«ùõ©¡þÜäõ¢£þö¿ 1.1 þ«ùµ│ò 1.2 õ¢£õ©║õ©Çþºìµèǵ£»þÜäþ«ùµ│ò ...5.4.1 þöƒµùѵéûÞ«║ 5.4.2 þÉâõ©ÄþøÆÕ¡É 5.4.3 Õ║ÅÕêù
- **ÞâîµÖ»**´╝ÜÚÇÜÞ┐絿íµïƒÕ«×Ú¬îµÄóÞ«¿þöƒµùѵéûÞ«║´╝îÕì│Õ£¿õ©Çþ¥ñÚÜŵ£║ÚÇëÕÅûþÜäõ║║õ©¡Þç│Õ░æõ©ñõ©¬õ║║þöƒµùÑþø©ÕÉîþÜ䵪éþÄçÚù«ÚóÿÒÇé - **Õ«×þÄ░µû╣µ│ò**´╝Ü - **ÚÜŵ£║þöƒµùÑþöƒµêÉ**´╝Üõ¢┐þö¿ÚÜŵ£║µò░þöƒµêÉÕ碵ò░µ¿íµïƒÚÜŵ£║þöƒµùÑÒÇé - **µ»öÞ¥âþöƒµùÑ**´╝ÜÚÇÜÞ┐çÕ¥¬þÄ»µ»öÞ¥âÚÜŵ£║þöƒµêÉ...
Þ»Ñõ╗úþáüµ╝öþñ║õ║åÕªéõ¢òõ¢┐þö¿Pythonþ╝ûÕåÖþ¿ïÕ║ŵØÑÞºúÕå│Õ«×ÚÖàÚù«Úóÿ´╝îÕàÀõ¢ôµØÑÞ»┤´╝îÕ«âÚÇÜÞ┐絿íµïƒÞ«íþ«ùÕ£¿õ©ÇÕ«Üõ║║µò░õ©ï´╝îµë¥Õê░õ©ñõ©¬ÕÉîõ©ÇÕñ®þöƒµùÑþÜ䵪éþÄç´╝îõ╗ÄÞÇîÕ╝òÕç║µªéþÄçÞ«║õ©¡þÜä"þöƒµùѵéûÞ«║"µªéÕ┐ÁÒÇéÞ┐Öõ©¬Úù«Úóÿõ©ìõ╗àÞÇâÚ¬îõ║åÕ»╣Õ¥¬þÄ»ÕÆîµØíõ╗ÂÕêñµû¡þ¡ëÕƒ║þíÇþ╝ûþ¿ïþ╗ôµ×äþÜä...