选择排序（selection sorts）算法大串讲

选择排序（selection sorts）算法大串讲

本文内容框架：

§1 选择排序

§2 锦标赛排序

  §3 堆排序

§4 Smooth Sort

§5 小结

 

 

 

§1 选择排序

选择排序(Selection sort)

 

选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。下图能够帮助很直观的理解出选择排序算法的思想：

 

 

 

void select_sort( int *a, int n)
{
    register int i, j, min, t;
    for( i = 0; i < n - 1; i ++)
    {
        min = i;
        //查找最小值
        for( j = i + 1; j < n; j ++)
            if( a[ min] > a[ j])
                min = j;
        //交换
        if( min != i)
        {
            t = a[ min];
            a[ min] = a[ i];
            a[ i] = t;
        }
    }
}

选择排序的交换操作介于和次之间。选择排序的比较操作为次之间。选择排序的赋值操作介于和次之间。比较次数O(n^2),比较次数与关键字的初始状态无关，总的比较次数N=(n-1)+(n-2)+...+1=n*(n-1)/2。 交换次数O(n),最好情况是，已经有序，交换0次；最坏情况是，逆序，交换n-1次。 交换次数比冒泡排序少多了，由于交换所需CPU时间比比较所需的CPU时间多，n值较小时，选择排序比冒泡排序快。

 

 

简单选择排序算法改进

传统的简单选择排序,每趟循环只能确定一个元素排序后的定位。我们可以考虑改进为每趟循环确定两个元素(当前趟最大和最小记录)的位置,从而减少排序所需的循环次数。改进后对n个数据进行排序,最多只需进行[n/2]趟循环即可。

 

 

 

 

§2 锦标赛排序

 

 

锦标赛排序（tournament iree sort）

 

直接选择排序要执行n-1趟（i=0，1，…，n-2），第i越要从n-i个对象中选出一个具有最小排序码的对象，需要进行n-i-1次排序码比较。当n比较大时，排序码比较次数相当多。这是因为在后一趟比较选择时，往往把前一趟已做过的比较又重复做了 一遍，没有把前一趟比较的结果保留下来。

　　锦标赛排序（tournament iree sort）克服了这一缺点。它的思想与体育比赛类似。首先取得n个对象的排序码，进行两两比较，得到[n／2]个比较的优胜者（排序码小者），作 为第一步比较的结果保留下来。然后对这[n／2]个对象再进行排序码的两两比较，……， 如此重复，直到选出一个排序码最小的对象为止。

 

#include <stdio.h> 
#include <stdlib.h> 
int _; 
#define swap(x, y) { _=x;x=y;y=_; } 
//#define max(x, y) ( ((x)>(y))?(x):(y) ) 
//#define min(x, y) ( ((x)<(y))?(x):(y) ) 
#define MAX (int)(((unsigned)(~((int)0)))>>1) 
#define MIN (-MAX-1) 
 
void Adjust(int *b, int x, int n) 
{ 
       int l = x * 2 + 1; 
       int r = l + 1; 
 
       //printf("%d\n", MAX); 
       if (l >= n) { 
              b[x] = MAX; 
              return; 
       } 
       else if (r >= n) { 
              b[x] = b[l]; 
              return; 
       } 
 
       if (b[l] == b[x]) { 
              Adjust(b, l, n); 
       } 
       else { 
              Adjust(b, r, n); 
       } 
       b[x] = min(b[l], b[r]); 
} 
 
void GameSort(int *a, int n) 
{ 
       int i, len, *b; 
       void Out(int *, int); 
 
       len = 1; 
       while (len < n) { 
              len <<= 1; 
       } 
       len = 2 * len - 1; 
       b = (int *)malloc(sizeof(int) * len); 
 
       for (i=len/2; i<len; i++) { 
              b[i] = (i-len/2<n) ? (a[i-len/2]) : (MAX); 
       } 
 
       for (i=len/2-1; i>=0; i--) { 
              b[i] = min(b[2 * i + 1], b[2 * i + 2]); 
       } 
       for (i=0; i<n; i++) { 
              a[i] = b[0]; 
              Out(b, len); //不断跟踪输出完全二叉树b[]状态 
              Adjust(b, 0, len); 
       } 
 
       free(b); 
} 
 
int main() 
{ 
       int a[] = { 21, 25, 49, 25, 16, 8, 63, 63, 100, 1002 }; 
       int i, n = 9; 
 
       for (i=0; i<n; i++) { 
              printf("%5d", a[i]); 
       } 
       printf("\n"); 
 
       GameSort(a, n); 
       for (i=0; i<n; i++) { 
              printf("%5d", a[i]); 
       } 
       printf("\n"); 
 
       return 0; 
} 
 
// ---- 输出部分, 与程序算法无关 ---- 
// ---- 为了打出那个树状, 好看 ---- 
 
#include <math.h> 
 
void Out(int *a, int n) 
{ 
       void _Out(int *, int); 
 
       //printf("%d===\n", n / 2 + 1); 
       _Out(a + (n / 2), n / 2 + 1); 
} 
 
void _Out(int *a, int n) 
{ 
       static int i, j, set = 0; 
       int len = log((double)n) / log((double)2) + 1; 
       int l, r, have; 
 
       int **b = (int **)malloc(sizeof(int *) * len); 
       for (i=0; i<len; i++) { 
              b[i] = (int *)malloc(sizeof(int) * n); 
              for (j=0; j<n; j++) { 
                     b[i][j] = MIN; 
              } 
       } 
 
       //printf("%d\n", MIN); 
       for (i=0; i<n; i++) { 
              b[len - 1][i] = a[i]; 
       } 
       for (i=len-1; i>=1; i--) { 
              have = 0; 
              for (j=0; j<n; j++) { 
                     if (b[i][j] != MIN) { 
                            (++have==1)?(l=j):(r=j); 
                     } 
                     if (have == 2) { 
                            b[i-1][(l+r)/2] = min(b[i][l], b[i][r]); 
                            have = 0; 
                     } 
              } 
       } 
 
       printf("\n ---- Set %d ----\n", set++); 
       for (i=0; i<len; i++) { 
              for (j=0; j<n; j++) { 
                     if (b[i][j] == MIN) { 
                            printf("    "); 
                     } 
                     else if (b[i][j] == MAX) { 
                            printf(" MAX"); 
                     } 
                     else { 
                            printf("  %02d", b[i][j]); 
                     } 
              } 
              printf("\n"); 
       } 
}

 

 

 

§3 堆排序

 

堆排序（heap sort）

锦标赛算法有两个缺点：辅助存储空间较多、最大值进行多余的比较。堆排序就是在锦标赛排序的基础上改进——只需要O(1)的辅助存储空间，减少最大值的比较。

 

二叉堆是完全二叉树或者是近似完全二叉树。

二叉堆满足二个特性：

1．父结点的键值总是大于或等于（小于或等于）任何一个子节点的键值。

2．每个结点的左子树和右子树都是一个二叉堆（都是最大堆或最小堆）。

当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。下图展示一个最小堆：

 

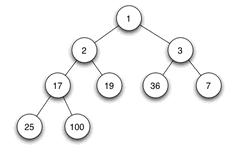
堆的存储

一般都用数组来表示堆，i结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如第0个结点左右子结点下标分别为1和2。

 

在堆的数据结构中，堆中的最大值总是位于根节点。堆中定义以下几种操作：

最大堆调整（Max_Heapify）：将堆的末端子结点作调整，使得子结点永远小于父结点

创建最大堆（Build_Max_Heap）：将堆所有数据重新排序

堆排序（HeapSort）：移除位在第一个数据的根结点，并做最大堆调整的递归运算

 

 

#include <cstdio>
#include <cstdlib>
#include <cmath>
 
const int HEAP_SIZE = 13; //堆大小
 
int parent(int);
int left(int);
int right(int);
void Max_Heapify(int [], int, int);
void Build_Max_Heap(int []);
void print(int []);
void HeapSort(int [], int);
 
/*父结点*/
int parent(int i)
{
    return (int)floor((i - 1) / 2);
}
 
/*左子结点*/
int left(int i)
{
    return (2 * i + 1);
}
 
/*右子结点*/
int right(int i)
{
    return (2 * i + 2);
}
 
/*从单一子结点创建最大堆*/
void Max_Heapify(int A[], int i, int heap_size)
{
    int l = left(i);
    int r = right(i);
    int largest;
    int temp;
    if(l < heap_size && A[l] > A[i])
    {
        largest = l;
    }
    else
    {
        largest = i;
    }
    if(r < heap_size && A[r] > A[largest])
    {
        largest = r;
    }
    if(largest != i)
    {
        temp = A[i];
        A[i] = A[largest];
        A[largest] = temp;
        Max_Heapify(A, largest, heap_size);
    }
}
 
/*建立最大堆*/
void Build_Max_Heap(int A[])
{
    for(int i = (HEAP_SIZE-1)/2; i >= 0; i--)
    {
        Max_Heapify(A, i, HEAP_SIZE);
    }
}
 
/*输出最大堆*/
void print(int A[])
{
    for(int i = 0; i < HEAP_SIZE;i++)
    {
        printf("%d ", A[i]);
    }
    printf("\n");
}
 
/*利用堆进行排序*/
void HeapSort(int A[], int heap_size)
{
    Build_Max_Heap(A);
    int temp;
    for(int i = heap_size - 1; i >= 0; i--)
    {
        temp = A[0];
        A[0] = A[i];
        A[i] = temp;
        Max_Heapify(A, 0, i);
    }
    print(A);
}
 
/*测试*/
int main(int argc, char* argv[])
{
    int A[HEAP_SIZE] = {19, 1, 10, 14, 16, 4, 7, 9, 3, 2, 8, 5, 11};
    HeapSort(A, HEAP_SIZE);
    system("pause");
    return 0;
}

 

堆的操作

堆的操作主要是插入和删除，插入总是将插入元素放在堆的末尾，然后进行恢复堆次序处理；删除操作是将要删除元素和最后一个元素替换，然后进行恢复堆次序处理。其实归根结底也是堆的调整操作，只是多了对堆大小（元素个数）的修改）。

 

 

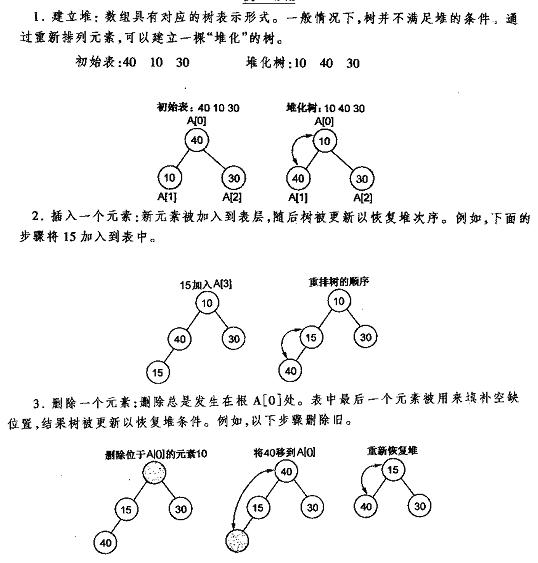
§4 Smooth Sort 

Smooth Sort算法

 

Smooth Sort基本思想和Heap Sort相同，但Smooth Sort使用的是一种由多个堆组成的优先队列，这种优先队列在取出最大元素后剩余元素可以就地调整成优先队列，所以Smooth Sort不用像Heap Sort那样反向地构建堆，在数据基本有序时可以达到O(n)复杂度。Smooth Sort算法在维基百科上有详细介绍。

　　  Smooth Sort是所有算法中时间复杂度理论值最好的，但由于Smooth Sort所用的优先队列是基于一种不平衡的结构，复杂度因子很大，所以该算法的实际效率并不是很好。

 

 

#include <cstdio>
 #include <cstdlib>
 #include <ctime>
 
 static unsigned int set_times = 0;
 static unsigned int cmp_times = 0;
 
 template<typename item_type> void setval(item_type& item1, item_type& item2) {
     set_times += 1;
     item1 = item2;
     return;
 }
 
 template<typename item_type> int compare(item_type& item1, item_type& item2) {
     cmp_times += 1;
     return item1 < item2;
 }
 
 template<typename item_type> void swap(item_type& item1, item_type& item2) {
     item_type item3;
 
     setval(item3, item1);
     setval(item1, item2);
     setval(item2, item3);
     return;
 }
 
 static const unsigned int leonardo[] = {
     1, 1, 3, 5, 9, 15, 25, 41, 67, 109, 177, 287, 465, 753, 1219, 1973,
     3193, 5167, 8361, 13529, 21891, 35421, 57313, 92735, 150049, 242785,
     392835, 635621, 1028457, 1664079, 2692537, 4356617, 7049155, 11405773,
     18454929, 29860703, 48315633, 78176337, 126491971, 204668309, 331160281,
     535828591, 866988873, 1402817465, 2269806339u, 3672623805u,
 };
 
 template<typename item_type> inline void smooth_sort_fix(
         item_type* array, int current_heap, int level_index, int* levels) {
     int prev_heap;
     int max_child;
     int child_heap1;
     int child_heap2;
     int current_level;
 
     while(level_index > 0) {
         prev_heap = current_heap - leonardo[levels[level_index]];
         if(compare(array[current_heap], array[prev_heap])) {
             if(levels[level_index] > 1) {
                 child_heap1 = current_heap - 1 - leonardo[levels[level_index] - 2];
                 child_heap2 = current_heap - 1;
                 if(compare(array[prev_heap], array[child_heap1])) break;
                 if(compare(array[prev_heap], array[child_heap2])) break;
             }
             swap(array[current_heap], array[prev_heap]);
             current_heap = prev_heap;
             level_index -= 1;
         } else break;
     }
 
     current_level = levels[level_index];
     while(current_level > 1) {
         max_child = current_heap;
         child_heap1 = current_heap - 1 - leonardo[current_level - 2];
         child_heap2 = current_heap - 1;
 
         if(compare(array[max_child], array[child_heap1])) max_child = child_heap1;
         if(compare(array[max_child], array[child_heap2])) max_child = child_heap2;
         if(max_child == child_heap1) {
             swap(array[current_heap], array[child_heap1]);
             current_heap = child_heap1;
             current_level -= 1;
         }
         else if(max_child == child_heap2) {
             swap(array[current_heap], array[child_heap2]);
             current_heap = child_heap2;
             current_level -= 2;
         } else break;
     }
     return;
 }
 
 template<typename item_type> void smooth_sort(item_type* array, int size) {
 
     int levels[64] = {1};
     int toplevel = 0;
     int i;
 
     for(i = 1; i < size; i++) {
         if(toplevel > 0 && levels[toplevel - 1] - levels[toplevel] == 1) {
             toplevel -= 1;
             levels[toplevel] += 1;
         } else if(levels[toplevel] != 1) {
             toplevel += 1;
             levels[toplevel] = 1;
         } else {
             toplevel += 1;
             levels[toplevel] = 0;
         }
         smooth_sort_fix(array, i, toplevel, levels);
     }
 
     for(i = size - 2; i > 0; i--) {
         if(levels[toplevel] <= 1) {
             toplevel -= 1;
         } else {
             levels[toplevel] -= 1;
             levels[toplevel + 1] = levels[toplevel] - 1;
             toplevel += 1;
 
             smooth_sort_fix(array, i - leonardo[levels[toplevel]], toplevel - 1, levels);
             smooth_sort_fix(array, i, toplevel, levels);
         }
     }
     return;
 }
 
 int main(int argc, char** argv) {
     int capacity = 0;
     int size = 0;
     int i;
     clock_t clock1;
     clock_t clock2;
     double data;
     double* array = NULL;
 
     // generate randomized test case
     while(scanf("%lf", &data) == 1) {
         if(size == capacity) {
             capacity = (size + 1) * 2;
             array = (double*)realloc(array, capacity * sizeof(double));
         }
         array[size++] = data;
     }
 
     // sort
     clock1 = clock();
     smooth_sort(array, size);
     clock2 = clock();
 
     // output test result
     fprintf(stderr, "smooth_sort:\t");
     fprintf(stderr, "time %.2lf\t", (double)(clock2 - clock1) / CLOCKS_PER_SEC);
     fprintf(stderr, "cmp_per_elem %.2lf\t", (double)cmp_times / size);
     fprintf(stderr, "set_per_elem %.2lf\n", (double)set_times / size);
     for(i = 0; i < size; i++) {
         fprintf(stdout, "%lf\n", array[i]);
     }
     free(array);
     return 0;
 }

 

 

 

§5 小结

这篇博文列举了选择排序的几个算法，管中窥豹，不求甚解。如果你有任何建议或者批评和补充，请留言指出，不胜感激，更多参考请移步互联网。

 

 

 

 

 

参考：

①MoreWindows： http://blog.csdn.net/morewindows/article/details/6709644

②RichSelian： http://www.cnblogs.com/richselian/archive/2011/09/16/2179148.html

③kapinter： http://zdker.blog.163.com/blog/static/584834200659636560/

④更多参考来着维基百科

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

评论

1 楼 zuhanbing 2013-11-19