1、幂级数
在数学中,幂级数是一类形式简单而应用广泛的函数级数,变量可以是一个或多个(见“多元幂级数”一节)。单变量的幂级数形式为:


其中的c和 是常数。
是常数。 称为幂级数的系数。幂级数中的每一项都是一个幂函数,幂次为非负整数。幂级数的形式很像多项式,在很多方面有类似的性质,可以被看成是“无穷次的多项式”。
称为幂级数的系数。幂级数中的每一项都是一个幂函数,幂次为非负整数。幂级数的形式很像多项式,在很多方面有类似的性质,可以被看成是“无穷次的多项式”。
如果把 看成一项,那么幂级数可以化简为
看成一项,那么幂级数可以化简为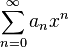 的形式。后者被称为幂级数的标准形式。一个标准形式的幂级数完全由它的系数来决定。
的形式。后者被称为幂级数的标准形式。一个标准形式的幂级数完全由它的系数来决定。
将一个函数写成幂级数  的形式称为将函数在c处展开成幂级数。不是每个函数都可以展开成幂级数。
的形式称为将函数在c处展开成幂级数。不是每个函数都可以展开成幂级数。
幂级数是分析学研究的重点之一,然而在组合数学中,幂级数也占有一席之地。作为母函数,由幂级数概念发展出来的形式幂级数是许多组合恒等式的来源[1]。在电力工程学中,幂级数则被称为Z-变换。实数的小数记法也可以被看做幂级数的一种,只不过这里的x被固定为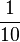 。在p-进数中则可以见到x被固定为
。在p-进数中则可以见到x被固定为 的幂级数。
的幂级数。
多项式可以看做系数从某一项开始全是零的幂级数,例如多项式  可以写成标准形式的幂级数:
可以写成标准形式的幂级数:

也可以写成( ):
):
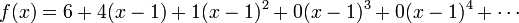
实际上,多项式可以写成在任意c附近展开的幂级数。就这个意义上说,幂级数是多项式的推广。
等比级数的公式给出了对 ,有
,有
 ,
,
是幂级数中基本而又重要的一类。同样重要的还有指数的幂级数展开:

以及正弦函数(对所有实数x 成立):
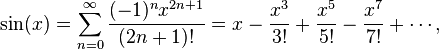
这些幂级数都属于泰勒级数。
幂级数里不包括负的幂次。例如 就不是幂级数(它是一个劳伦级数)。同样的,幂次为分数的级数也不是幂级数。系数
就不是幂级数(它是一个劳伦级数)。同样的,幂次为分数的级数也不是幂级数。系数 必须是和x无关,比如
必须是和x无关,比如 就不是一个幂级数。
就不是一个幂级数。
2、母函数
在数学中,某个序列 的母函数是一种形式幂级数,其每一项的系数可以提供关于这个序列的信息。使用母函数解决问题的方法称为母函数方法。
的母函数是一种形式幂级数,其每一项的系数可以提供关于这个序列的信息。使用母函数解决问题的方法称为母函数方法。
母函数可分为很多种,包括普通母函数、指数母函数、L级数、贝尔级数和狄利克雷级数。对每个序列都可以写出以上每个类型的一个母函数。构造母函数的目的一般是为了解决某个特定的问题,因此选用何种母函数视乎序列本身的特性和问题的类型。
母函数的表示一般使用解析形式,即写成关于某个形式变量x的形式幂级数。对幂级数的收敛半径中的某一点,可以求母函数在这一点的级数和。但无论如何,由于母函数是形式幂级数的一种,其级数和不一定对每个x的值都存在。
母函数方法不仅在概率论的计算中有重要地位,而且已成为组合数学中一种重要方法。此外,母函数在有限差分计算、特殊函数论等数学领域中都有着广泛的应用。
分享到:












![deepfuture的博客: 深未来(深度创造未来)[deepfuture@yeah.net] deepfuture的博客](https://www.iteye.com/upload/logo/user/690059/d08c7f3a-9298-3a06-9235-0d0226833f0a.jpg?1717538039)



 是常数。
是常数。 看成一项,那么幂级数可以化简为
看成一项,那么幂级数可以化简为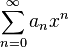 的形式。后者被称为幂级数的标准形式。一个标准形式的幂级数完全由它的系数来决定。
的形式。后者被称为幂级数的标准形式。一个标准形式的幂级数完全由它的系数来决定。 的形式称为将函数在c处展开成幂级数。不是每个函数都可以展开成幂级数。
的形式称为将函数在c处展开成幂级数。不是每个函数都可以展开成幂级数。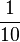 。在p-进数中则可以见到x被固定为
。在p-进数中则可以见到x被固定为 的幂级数。
的幂级数。 可以写成标准形式的幂级数:
可以写成标准形式的幂级数:
 ):
):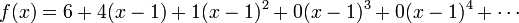
 ,有
,有 ,
,
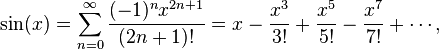
 就不是幂级数(它是一个劳伦级数)。同样的,幂次为分数的级数也不是幂级数。系数
就不是幂级数(它是一个劳伦级数)。同样的,幂次为分数的级数也不是幂级数。系数 必须是和x无关,比如
必须是和x无关,比如 就不是一个幂级数。
就不是一个幂级数。 的母函数是一种形式幂级数,其每一项的系数可以提供关于这个序列的信息。使用母函数解决问题的方法称为母函数方法。
的母函数是一种形式幂级数,其每一项的系数可以提供关于这个序列的信息。使用母函数解决问题的方法称为母函数方法。


相关推荐
母函数,又称生成函数,是数学中一种强大的工具,特别是在组合数学和数论领域中,它被用来表示和处理序列的结构和性质。母函数通过将序列的每一项与一个对应的变量的幂次相乘,然后求和,来构建一个形式上的多项式。...
母函数,又称生成函数,是数学中用于处理序列或序列系数的一种强大工具,特别是在组合数学和分析数论中。母函数的基本思想是将一个数列的系数转化为一个多项式或者函数,通过操作这个函数来研究数列的性质,如求和、...
母函数是数学中用于处理序列的一种工具,尤其在组合数学和计算机科学中有着广泛的应用。母函数的概念源自序列与其生成函数的对应关系。对于一个序列{an},它的母函数G(x)是一个形式上的幂级数,其中G(x)的系数对应着...
母函数是数学中的一种工具,尤其在组合数学和序列分析中有着广泛的应用。它通过将一个序列的项组合成一个多项式来表示整个序列。在讲座"母函数及其应用_new.ppt"中,讲师刘春英讲解了如何利用母函数解决实际问题,如...
勒让德母函数,全称为勒让德多项式的一般化母函数,是数学中一个极其重要的特殊函数,尤其在物理学、工程学和数值分析等领域有着广泛的应用。它与勒让德多项式密切相关,后者是一组正交的多项式序列,通常用在解决...
母函数在数学中是一种强大的工具,特别是在组合数学和序列分析中。它可以帮助我们处理和求解整数拆分、多项式相乘等复杂问题。母函数的概念源于序列的生成,通过对序列的每个项进行加权并形成一个多项式来表示整个...
母函数性质及其应用 母函数是概率论和数理统计中一个重要的数学工具,它是研究随机过程和随机变量的分布特性的一种数学表示方法。母函数的性质和应用广泛地应用于统计学、机器学习、计算机科学、工程学等领域。 一...
非常好的 概率论中 关于特征函数 和 矩母函数的介绍;
母函数,又称生成函数,在数学领域,特别是在组合数学和算法设计中扮演着至关重要的角色。它是将序列与其相应的多项式关联起来的一种方法,通过这种方式,我们可以利用多项式的运算来研究和解决问题,尤其在处理计数...
### 母函数在求解卡特兰数中的应用 #### 一、母函数与卡特兰数的基础概念 在组合数学中,**母函数**是一种用来表示序列的方法,通过构造一个函数使得该函数的系数对应原序列的值。利用母函数可以非常方便地解决...
【母函数】是数学中的一种工具,特别是在组合数学和算法竞赛中被广泛应用。母函数的概念源于序列的生成函数,它可以用来表示和分析一系列数字的关系。在ACM(国际大学生程序设计竞赛)的学习中,掌握母函数是解决...
母函数的性质及应用在离散数学领域占据着极其重要的地位,它不仅是连接离散与连续数学的桥梁,更是处理数列与组合计数问题的强大工具。本文将深入探讨母函数的基本概念、性质及其在信息学竞赛中的广泛应用,旨在帮助...
### 组合数学中的母函数与递推关系 #### 一、引言 组合数学是一门研究离散对象的科学,其关注的是如何选择、排列这些对象的方式。母函数是组合数学中的一个重要工具,它可以帮助我们解决许多组合问题,尤其是与...
母函数,又称生成函数,在数学和计算机科学中是一种强大的工具,尤其在处理序列和递推关系时。通过母函数,我们可以将一个序列的性质转换成一个解析表达式,从而简化问题的解决。母函数的概念源自组合数学,它可以...
母函数作为解决计数问题的一种工具,被广泛应用于处理各种组合问题,尤其是在计算复杂组合计数时。本文将详细介绍母函数的概念及其在ACM竞赛中的应用。 ### 普通型母函数 普通型母函数源于二项式定理,它表示的是...
积分变换与矩母函数关系涉及到数学中对函数进行操作以产生新函数的多种变换方法,这些方法在各种计算中非常有用,并且通常被称为变换。在这些变换中,积分变换是通过积分过程为主导的变换方式,而矩母函数则是在...
在计算机科学领域,特别是算法竞赛(如ACM/ICPC)中,母函数和动态规划是两种非常重要的解决复杂问题的工具。它们都是数学方法在编程中的应用,可以帮助我们高效地处理各种计算问题。 首先,让我们来深入了解一下...
母函数方法是一套非常有用的方法,应用极广。这套方法的系统叙述,最早见于Laplace在1812年的名著—概率解析理论。
### 使用母函数方法解题(离散数学) #### 概述 母函数是离散数学中一种强大的工具,尤其在解决排列组合问题以及求解递推关系时展现出其独特的优势。这种方法不仅能够简化复杂的数学计算,还能提供一种系统性的...
"母函数"是数学中一个强大的工具,特别适用于处理离散问题和组合优化问题,它在ACM训练中有着广泛的应用。母函数,也称为生成函数,是一种将序列的项与多项式系数对应的方法,能够简洁地表达和操作序列。 母函数的...