- 浏览: 289961 次
- 性别:

- 来自: 济南
-

文章分类
最新评论
08年9月入学,12年7月毕业,结束了我在软件学院愉快丰富的大学生活。此系列是对四年专业课程学习的回顾,索引参见:http://blog.csdn.net/xiaowei_cqu/article/details/7747205
排序算法
排序是非常常用,非常基本的算法。排序的方法有很多,比如插入排序、选择排序、希尔排序、归并排序、快速排序、堆排序。
本次试验重点实现:希尔排序、归并排序、快速排序、堆排序
插入排序
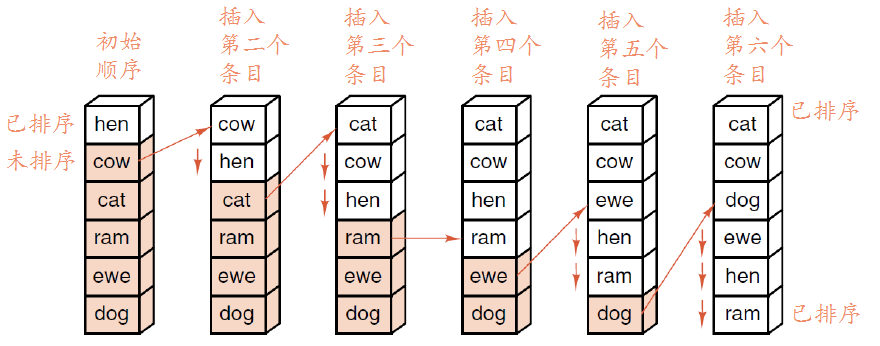
简单说就是每次选未排序的队列中最小的条目插入到已排序队列的最后:
选择排序
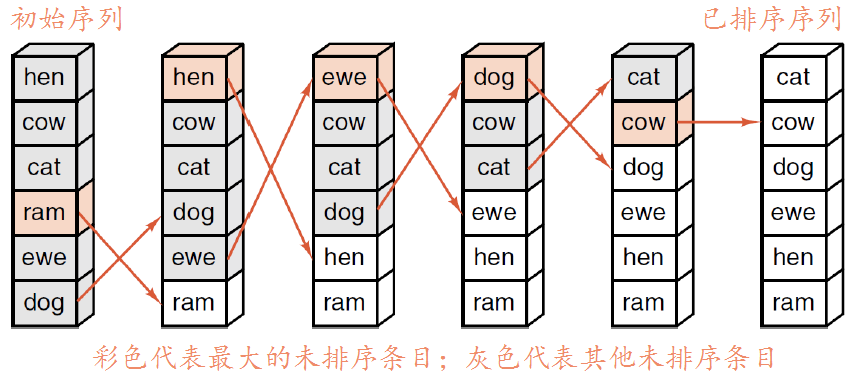
选择排序和插入有点像,是每次从拿未排序中的第一个条目插入到已排序中应该插入的位置:
希尔排序
希尔排序是插入排序的一种,是针对直接插入排序算法的改进。
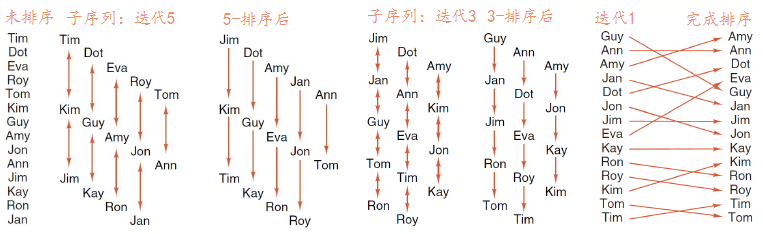
希尔排序的基本思想是:先取一个小于count的增量increment,把表中Record分为increment组,所有距离为increment的Record为同一组,现在各组中进行直接插入排序(insert_sort),然后减小increment重复分组和排序,知道increment=1,即所有Record放在同一组中进行直接插入排序为止。
希尔排序的基本思想是:先取一个小于count的增量increment,把表中Record分为increment组,所有距离为increment的Record为同一组,现在各组中进行直接插入排序(insert_sort),然后减小increment重复分组和排序,知道increment=1,即所有Record放在同一组中进行直接插入排序为止。
【相关实验】
首先从类表List中派生子表Sortable_list。为了方便定义,我们可以重载这样的构造函数
template<class Record>
Sortable_list<Record>::Sortable_list(const Record A[],int size)
{
for(int i=0;i<size;i++)
insert(i,A[i]);
}
1.编写函数shell_sort。函数中我们从首先定义increment=0,观察题目要求,可以得到在循环中有这样的关系increment=increment/2;使用循环将每次分组后的每组排列,排列我们再增加函数sort_interval();在每组的排序中使用的直接插入排序,所以可以这样实现sort_interval:每次定义一个临时的Sortable_list对象tmp记录每次分组的小组,对tmp使用insertion_sort,进而我们编写函数insertion_sort();2.实现表的排序一个重要的步骤是将Record换到相应位置,即交换,所以编写函数swap;
3.为了输出每趟排序结果,我们再编写一个全局函数print_out,由List的成员函数traverse()调用;调用的过程在置于swap之中,即每次有交换(或看做移动)则看做一趟排序。
相应算法函数如下:
template<class Record>
void Sortable_list<Record>::shell_sort()
/*Post: The entries of the Sortable_list have been rearranged so that the keys in
all the entries are sorted into nondecreasing order.
Uses: sort_interval.
*/
{
int increment, //spacing of entries in sublist
start; //starting point of sublist
increment=count;
do{
increment=increment/2;
for(start=0;start<increment;start++){
sort_interval(start,increment); //modified insertion sort
traverse(print_out);
cout<<endl;
}
}while(increment>1);
}
template<class Record>
void Sortable_list<Record>::sort_interval(int start,int increment)
{
Sortable_list<Record> temp;
int j=0;
for(int i=start;i<size();i=i+increment){
Record temp_record;
retrieve(i,temp_record);
temp.insert(j,temp_record);
j++;
}
temp.insertion_sort();
j=0;
for(int k=start;k<size();k+=increment){
Record temp_record;
temp.retrieve(j,temp_record);
replace(k,temp_record);
j++;
}
}
template<class Record>
void Sortable_list<Record>::insertion_sort()
/*Post: The entries of the Sortable_list have been rearranged so that the keys in
all the entries are sorted into nondecreasing order.
Uses: Methods for the class Record; the contiguous List
*/
{
int first_unsorted; //position of first unsorted entry
int position; //searches sorted part of list
Record current; //holds the entry emporarily removed from list
for(first_unsorted=1;first_unsorted<count;first_unsorted++)
if(entry[first_unsorted]<entry[first_unsorted-1]){
position=first_unsorted;
current=entry[first_unsorted]; //Pull unsorted entry out of the list.
do{ //Shift all entries until the proper position is found
entry[position]=entry[position-1];
position--; //position if empty.
}while(position>0&&entry[position-1]>current);
entry[position]=current;
}
}
//其他辅助函数见源文件
【实验结果】
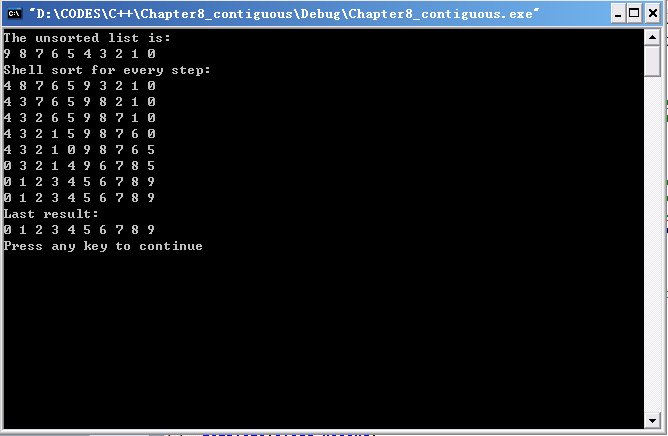
归并排序
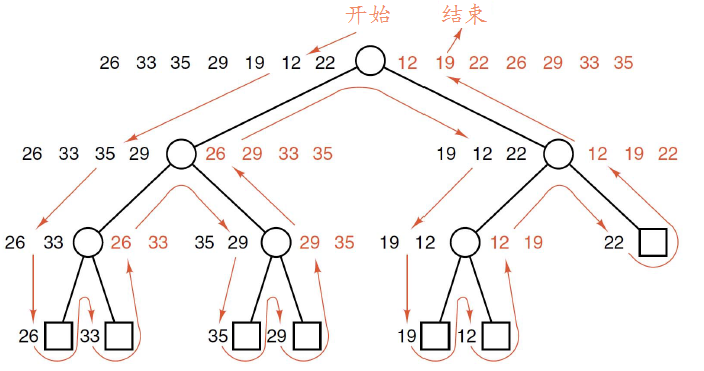
归并排序是采用分治的思想将两个已排序的表合并成一个表
归并排序算法的基本思想是:先将一个表分成两个表(当个数是奇数时,使左表的元素比右表多一)。对两个表分别进行归并排序,然后将两个已排序好的表合并。合并的思路就像将两罗纸牌混成一摞,每次取顶上最小的纸牌。
归并排序算法的基本思想是:先将一个表分成两个表(当个数是奇数时,使左表的元素比右表多一)。对两个表分别进行归并排序,然后将两个已排序好的表合并。合并的思路就像将两罗纸牌混成一摞,每次取顶上最小的纸牌。
【相关实验】
1.仍旧使用上述的Sortable_list
2.根据归并排序的思想,每次子表仍旧使用归并排序,可以通过递归实现。所以编写递归函数recursive_merge_sort(),要把已排序好的子表合并,所以编写合并子表的辅助函数merge()
3.为了输出每趟排序结果,在归并时merge中加入traverse(print_out) //但因为递归调用的问题,很多次我们还是看不到过程
2.根据归并排序的思想,每次子表仍旧使用归并排序,可以通过递归实现。所以编写递归函数recursive_merge_sort(),要把已排序好的子表合并,所以编写合并子表的辅助函数merge()
3.为了输出每趟排序结果,在归并时merge中加入traverse(print_out) //但因为递归调用的问题,很多次我们还是看不到过程
template<class Record>
void Sortable_list<Record>::merge(int low,int high)
{
Record *tmp=new Record[high-low+1];
int index=0;
int index1=low,mid=(low+high)/2,index2=mid+1;
while(index1<=mid&&index2<=high){
if(entry[index1]<entry[index2])
tmp[index++]=entry[index1++];
else
tmp[index++]=entry[index2++];
}
while(index1<=mid)
tmp[index++]=entry[index1++];
while(index2<=high)
tmp[index++]=entry[index2++];
for(index=low;index<=high;index++)
entry[index]=tmp[index-low];
delete []tmp;
traverse(print_out);
cout<<endl;
}
template<class Record>
void Sortable_list<Record>::recursive_merge_sort(int low,int high)
/*Post: The entries of the sortable list between
index low and high have been rearranged so that
their keys are sorted into nondecreasing order.
Uses: The contiguous list
*/
{
if(high>low){
recursive_merge_sort(low,(high+low)/2);
recursive_merge_sort((high+low)/2+1,high);
merge(low,high);
}
}
template<class Record>
void Sortable_list<Record>::merge_sort()
/* Post: The entries of the sortable list have been rearranged so that
their keys are sorted into nondecreasing order.
Uses: The contiguous list
*/
{
recursive_merge_sort(0,size()-1);
}
【实验结果】
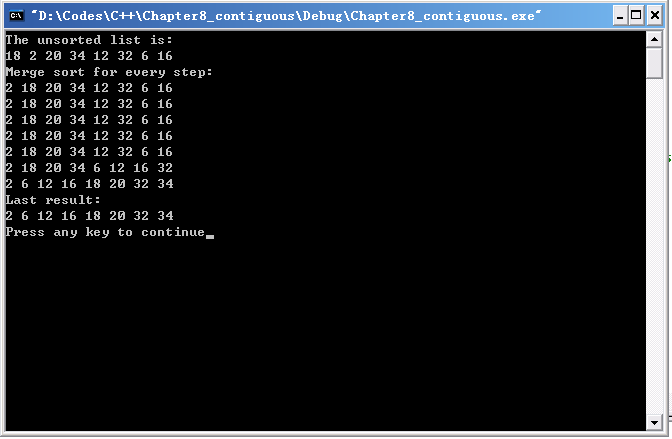
快速排序
快速排序是对冒泡排序的一种改进。
快速排序算法的基本思想是:每一趟排序中找一个点pivot,将表分割成独立的两部分,其中一部分的所有Record都比pivot小,另一部分比pivot大,然后再按此方法对这两部分数据分别进行快速排序。
快速排序算法的基本思想是:每一趟排序中找一个点pivot,将表分割成独立的两部分,其中一部分的所有Record都比pivot小,另一部分比pivot大,然后再按此方法对这两部分数据分别进行快速排序。
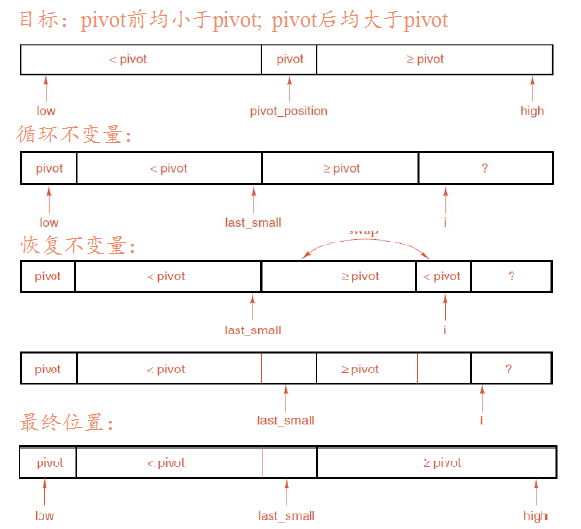
【相关实验】
1.仍旧使用上述的Sortable_list。
2.根据快速排序的思想,每趟排序将表分成两部分然后仍旧进行快速排序,所以可以通过递归实现,而为了调用递归函数,我们首先编写给定要排序范围的参数的函数recursive_quick_sort(int low,int high)//之所以不将开始的quick_sort直接写作递归函数,是为了避免输入参数而方便用户调用。另外需要一个partition函数,返回每趟排序之后的分点。
3.为了输出每趟排序,我的想法是在每次递归中使用traverse(print_out)输出,但却不是想象的结果。因为递归是每次递归出来之后才执行函数print_out,除了前几次可以看到结构,后来都是在排序好之后…所以我们仍旧通过swap函数实现输出。
2.根据快速排序的思想,每趟排序将表分成两部分然后仍旧进行快速排序,所以可以通过递归实现,而为了调用递归函数,我们首先编写给定要排序范围的参数的函数recursive_quick_sort(int low,int high)//之所以不将开始的quick_sort直接写作递归函数,是为了避免输入参数而方便用户调用。另外需要一个partition函数,返回每趟排序之后的分点。
3.为了输出每趟排序,我的想法是在每次递归中使用traverse(print_out)输出,但却不是想象的结果。因为递归是每次递归出来之后才执行函数print_out,除了前几次可以看到结构,后来都是在排序好之后…所以我们仍旧通过swap函数实现输出。
template<class Record>
int Sortable_list<Record>::partition(int low,int high)
/*Pre: low and high are valid positions of the Sortable_list, with low<=high.
Post: The center (or left center) entry in the range between indices low and
high of the Sortable_list has been chosen as a pivot. All entries of the
Sortable_list between indices low and high, inclusive, have been rearranged
so that chosen with keys less than the pivot com before the pivot
and the remaining entries come after the pivot. The final position of the
pivot is returned.
Uses: swap(int,int j) contigious list
*/
{
Record pivot;
int i, //used to scan through the list
last_small; //position of the last key less than pivot
swap(low,(low+high)/2);
pivot=entry[low];
last_small=low;
for(i=low+1;i<=high;i++)
//At the beginning of each iteration of this loop, we have the following conditions:
// If low<j<=last_samll then entry[j].key<pivot
// If last_small<j<i then entry[j].key>=pivot.
if(entry[i]<pivot){
last_small=last_small+1;
swap(last_small,i); //Move large entry to right and small to left
}
swap(low,last_small); //Put the pivot into its proper position.
return last_small;
}
template<class Record>
void Sortable_list<Record>::recursive_quick_sort(int low,int high)
/*Pre: low and high are valid positions in the Sortable list.
Post: The entries of the Sortable_list have been rearranged so that their keys
are sorted into nondecreasing order.
Uses: The contiguous list, recursive_quick_sort, partition.
*/
{
int pivot_postion;
if(low<high){
pivot_postion=partition(low,high);
recursive_quick_sort(low,pivot_postion-1);
recursive_quick_sort(pivot_postion+1,high);
}
}
template<class Record>
void Sortable_list<Record>::quick_sort()
{
recursive_quick_sort(0,count-1);
}
//其他函数见源码
【实验结果】
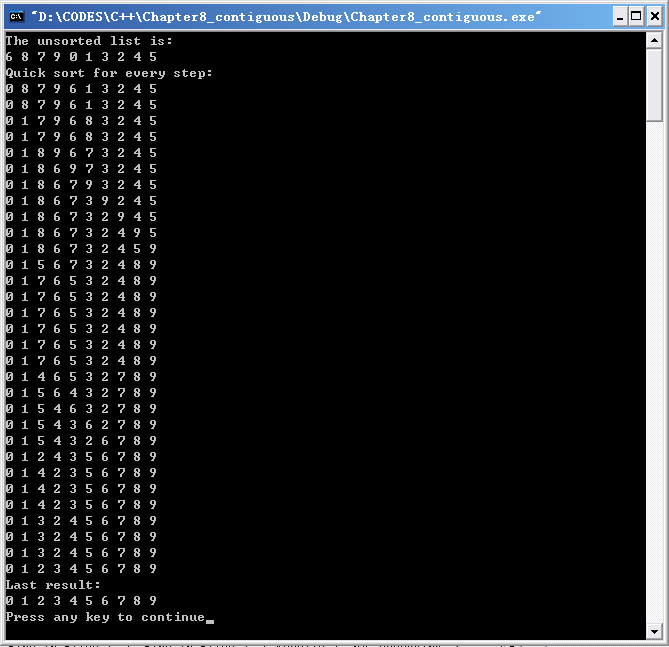
堆排序
堆排序是先将表中Record按大堆(或小堆)存放,使选取最大的Record变的极为容易,每次选取之后再提升堆。实现排序。
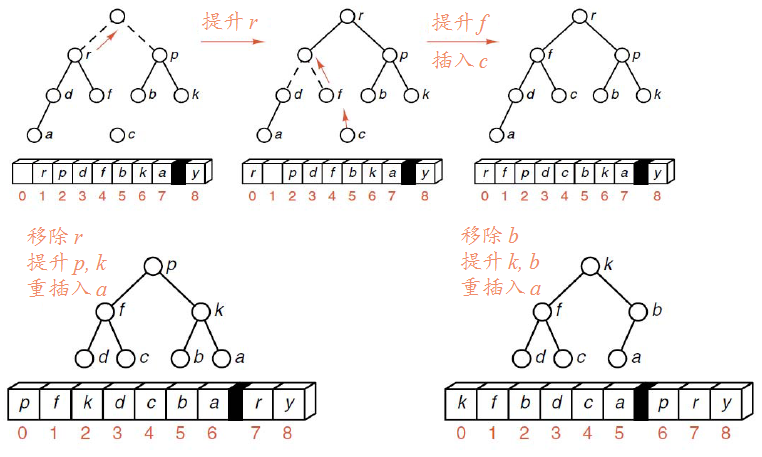
继续:
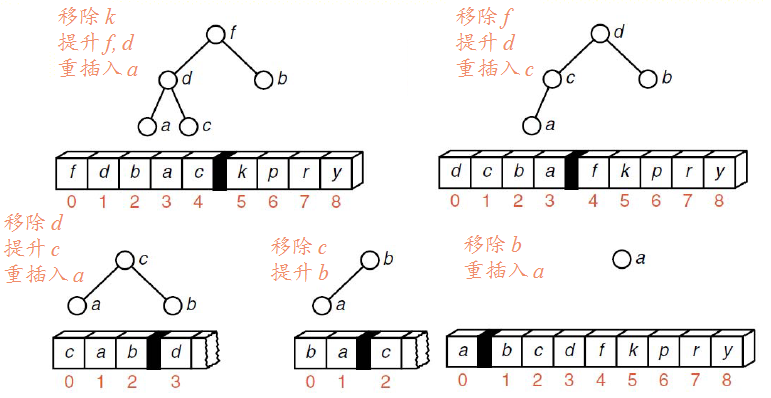
【相关实验】
1.仍旧使用上述的Sortable_list。
2.编写heap_sort()函数。按思路,首先应该建堆,然后取堆顶元素,之后对剩下元素重新建堆(提升堆),所以我们需要编写build_heap()函数,其通过inster_heap函数将元素一个个插入堆中。
最后实现heap_sort函数。
3.我们在每次插入堆时调用traverse(print_sort)实现对每趟排序的输出。
2.编写heap_sort()函数。按思路,首先应该建堆,然后取堆顶元素,之后对剩下元素重新建堆(提升堆),所以我们需要编写build_heap()函数,其通过inster_heap函数将元素一个个插入堆中。
最后实现heap_sort函数。
3.我们在每次插入堆时调用traverse(print_sort)实现对每趟排序的输出。
template<class Record>
void Sortable_list<Record>::insert_heap(const Record ¤t,int low,int high)
/*Pre: The entries of the Sortable_list between indices low+1 and high,
inclusive,form a heap. The entry in position low will be discarded.
Post: The entry current has been inserted into the Sortabl_list and the entries,
rearranged so that the entries between indices low and high, inclusive
form a heap.
*/
{
int large; //position of child of entry[low] with the larger key
large=2*low+1; //large is now the left child of low
while(large<=high){
if(large<high&&entry[large]<entry[large+1])
large++; //large is now the child of low with the largest key.
if(current>=entry[large])
break; //current belongs in position low
else{ //Promote entry[large] and move down the tree
entry[low]=entry[large];
low=large;
large=2*low+1;
}
}
entry[low]=current;
traverse(print_out);
cout<<endl;
}
template<class Record>
void Sortable_list<Record>::build_heap()
/*Post: The entries of the Sortable_list have been rearranged so that
it becomes a heap
Uses: The contiguous list and insert_heap
*/
{
int low;
for(low=count/2-1;low>=0;low--){
Record current=entry[low];
insert_heap(current,low,count-1);
}
}
template<class Record>
void Sortable_list<Record>::heap_sort()
/*Post: The entries of the Sortable_list have been rearranged so that their keys
are sorted into nondecreasing order.
Uses: The contiguous list, build_heap, insert_heap
*/
{
Record current; //temporary storage for moving entries
int last_unsorted; //Entries beyond last_unsorted have been sorted.
build_heap(); //First phase: Turn the list into a heap
for(last_unsorted=count-1;last_unsorted>0;last_unsorted--){
current=entry[last_unsorted]; //Extract the last entry from the list
entry[last_unsorted]=entry[0]; //Move top of heap to the end
insert_heap(current,0,last_unsorted-1); //Restore the heap
}
}
//其他函数见源码
【实验结果】
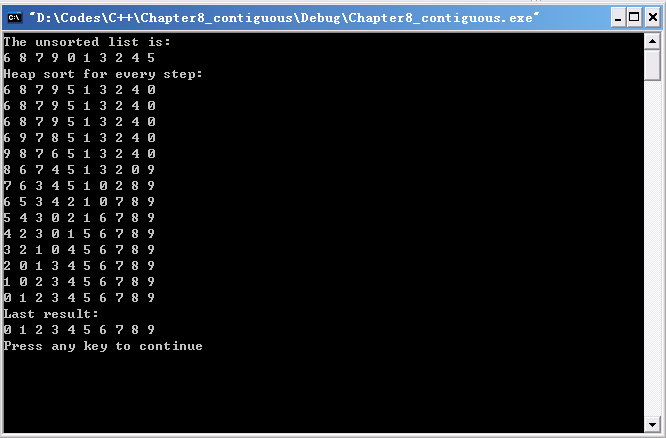
结果分析
【希尔排序】
1.希尔排序是直接插入的一种改进,在效率上较直接插入排序有较大的改进。直接插入排序每次只能将Record移动一个位置,即增量increment为1,而希尔排序开始时增量较大,分组较多,每组Record数目少,故各组内直接插入较快;increment递减之后分组逐渐减少,Record增多,但由于已经在increment较大时进行过排序,表更接近于有序状态,新一趟的排序也较快。
2.我在实验中子表的排序是通过定义一个新表,然后调用直接插入函数。但这种方法效率并不高,而且浪费空间;直接对子表进行直接插入的排序是一种更好的方法。
3.希尔排序复杂度为:O(nlog2n) d =1希尔与直接插入排序基本一致
4.希尔排序是不稳定的排序算法,即相等元素的顺序可能改变
【归并排序】
1.归并排序在实现上用链式表更为合理,因为合并中需要定义新的表,即使我们通过动态定义再删除,以节省不必要的空间,这些工作仍是有些费时。而链式表只是返回指针,对节点Node的Node<Node_entry>*next部分进行操作,不需要数据的移动。但同时链式表的使用也需要对指针有熟悉的掌握,很容易出错,先画图再编码往往会有更清晰的思路。2.归并排序的复杂度为:O(nlog2n)
3.归并排序是稳定的排序算法,即相等元素的顺序不会改变
【快速排序】
1.复杂度:最好 O(nlog2n),最坏 O(n2)2.快速排序的最坏情况基于每次划分对主元的选择。基本的快速排序选取第一个元素作为主元。这样在数组已经有序的情况下,每次划分将得到最坏的结果。一种比较常见的优化方法是随机化算法,即随机选取一个元素作为主元。这种情况下虽然最坏情况仍然是O(n^2),但最坏情况不再依赖于输入数据,而是由于随机函数取值不佳。
3.快速排序是一种不稳定的排序算法
【堆排序】
1.实现堆排序很重要的一个操作就是建堆要将初始表调整为一个大根堆,就必须将它所对应的完全二叉树中以每一结点为根的子树都调整为堆。显然只有一个结点的树是堆,而在完全二叉树中,所有序号大于n/2的结点都是叶子,因此以这些结点为根的子树均已是堆。这样,我们只需依次将以序号为n/2,…,1的结点作为根的子树都调整为堆即可。
2.堆[排序的时间,主要由建立初始堆和反复重建堆这两部分的时间开销构成,堆排序的最坏时间复杂度为O(nlog2n)。
3.堆排序是不稳定的排序算法
4.由于建初始堆所需的比较次数较多,所以堆排序不适宜于记录数较少的文件。
堆排序每次在大堆中直接选择出顶即最大的元素,这与选择排序极为相似,但他们是不同的,堆排序的性能更为优越。因为选择排序中,为了从表中选出最小的记录,必须进行n-1次比较,然后在剩余表中选出关键字最小的记录,又需要做n-2次比较。事实上,后面的n-2次比较中,有许多比较可能在前面的n-1次比较中已经做过,但由于前一趟排序时未保留这些比较结果,所以后一趟排序时又重复执行了这些比较操作。堆排序可通过树形结构保存部分比较结果,可减少比较次数。
(转载请注明作者和出处:http://blog.csdn.net/xiaowei_cqu 未经允许请勿用于商业用途)
发表评论
-
unity基础开发----物体位移和旋转实用代码
2013-11-21 22:46 1284using UnityEngine; using Syst ... -
Android中View绘制优化之一---- 优化布局层次
2012-09-04 23:00 1116... -
Android中View绘制优化二一---- 使用<include />标签复用布局文件
2012-09-08 13:54 1084... -
Android中View绘制优化之三---- 优化View
2012-09-13 21:00 1101... -
兰林任务管理应用程序雏形版以及概要说明
2012-09-15 21:54 900... -
Android中measure过程、WRAP_CONTENT详解以及xml布局文件解析流程浅析(上)
2012-10-10 18:14 1202... -
Android中measure过程、WRAP_CONTENT详解以及xml布局文件解析流程浅析(下)
2012-10-17 20:05 886... -
Android中文件选择器的实现
2012-11-30 08:59 1211... -
【编译原理】使用Lex将C/C++文件输出为HTML文件
2012-07-20 09:37 111008年9月入学,12年7月毕业,结束了我在软件学院愉快丰富的大 ... -
【编译原理】正则表达式
2012-07-21 21:49 236808年9月入学,12年7月毕业,结束了我在软件学院愉快丰富的大 ... -
【OpenCV】访问Mat图像中每个像素的值
2012-07-22 07:10 1218今天百度搜资料还搜到了自己的。。。《访问图像中每个像素的值 ... -
【编译原理】用Yacc做语法分析
2012-07-23 05:47 183208年9月入学,12年7月毕� ... -
【UML】UML几种图的绘制
2012-07-24 09:49 100908年9月入学,12年7月毕业,结束了我在软件学院愉快丰富的大 ... -
【OpenCV】邻域滤波:方框、高斯、中值、双边滤波
2012-07-26 10:52 1493邻域滤波(卷积) 邻域算子值利用给定像素 ... -
【OpenCV】角点检测:Harris角点及Shi-Tomasi角点检测
2012-07-31 13:25 1566角点 特征检测与匹配� ... -
【UML】案例分析:机场运作系统
2012-08-01 17:22 317508年9月入学,12年7月毕� ... -
【OpenCV】边缘检测:Sobel、拉普拉斯算子
2012-08-04 13:41 1584边缘 边缘(edge)是指图像局部强度变化最显著的部分。主要 ... -
【OpenCV】Canny 边缘检测
2012-08-08 10:17 2024Canny 边缘检测算法 1986� ... -
【UML】案例分析:新型超市购物自助系统
2012-08-19 01:13 131308年9月入学,12年7月毕业,结束了我在软件学院愉快丰富的大 ... -
【数据结构】二叉树、AVL树
2012-08-21 00:30 111608年9月入学,12年7月毕业,结束了我在软件学院愉快丰富的大 ...





相关推荐
7. 堆排序:利用了二叉堆的数据结构,可以看作是完全二叉树的数组表示。首先构造一个大顶堆(或小顶堆),然后将堆顶元素与末尾元素交换,接着对剩余元素重新调整为堆,重复此过程,直到所有元素都被排序。 这七种...
实现以下常用的内部排序算法并进行性能比较:"直接插入排序"," 折半插入排序"," 2—路插入排序"," 表插入排序"," 希尔排序"," 起泡排序"," 快速排序"," 简单选择排序"," 树形选择排序"," 堆排序"," 归并排序"," 链式...
本文将深入探讨Java编程语言中实现的七种主要排序算法:直接插入排序、希尔排序、选择排序、堆排序、冒泡排序、快速排序以及归并排序。每种算法都有其独特性,适用于不同的场景和数据特性。 1. **直接插入排序**:...
本文将详细介绍C++中实现的希尔排序、快速排序、堆排序和归并排序这四种经典排序算法。 希尔排序,由Donald Shell于1959年提出,是一种改进的插入排序。它的基本思想是通过设置一个增量序列,将待排序的元素按照...
本文将对快速排序、归并排序、堆排序等常见排序算法进行比较和分析,探讨它们的优缺点和适用场景。 首先, let's 看一下这些排序算法的时间复杂度和空间复杂度: | 排序算法 | 平均情况 | 最好情况 | 最坏情况 | ...
本篇文章将深入探讨标题和描述中提到的九大排序算法:快速排序、冒泡排序、堆排序、希尔排序、直接插入排序、直接选择排序、基数排序、箱排序和桶排序。 1. **快速排序**:快速排序是一种基于分治策略的排序算法,...
本篇文章将详细探讨基数排序、归并排序、堆排序、快速排序以及希尔排序这五种常见的排序算法,理解它们的基本思想以及实现方式。 1. **基数排序**: - **基本思想**:基数排序是一种非比较型整数排序算法,其原理...
7. 快速排序:快速排序由C.A.R. Hoare提出,采用分治策略,选取一个基准元素,将数组分为两部分,一部分所有元素小于基准,另一部分所有元素大于基准,然后对这两部分分别进行快速排序。平均时间复杂度为O(n log n)...
这七种算法分别是:冒泡排序、选择排序、直接插入排序、希尔排序、堆排序、归并排序和快速排序。 1. **冒泡排序**: 冒泡排序是最基础的排序算法之一,通过重复遍历待排序序列,比较相邻元素并交换位置来实现排序...
这里我们将深入探讨六种基本的排序算法:冒泡排序、插入排序、选择排序、希尔排序、堆排序以及归并排序,这些都是快速排序算法的基础。下面,我们将逐一介绍这些算法的工作原理、效率特点及其应用场景。 1. **冒泡...
本主题将详细探讨希尔排序、冒泡排序、堆排序等经典的排序算法,这些都是数据结构与算法学习中的核心内容,尤其对于北邮数据结构课程来说,理解并掌握这些排序方法至关重要。 1. **插入排序**: 插入排序是一种...
本项目重点实现了四种常见的排序算法:希尔排序、快速排序、堆排序以及归并排序,并将这些算法应用于随机生成的10000个整数上。以下是这四种排序算法的详细解释: 1. **希尔排序**: 希尔排序,又称插入排序的改进...
堆排序是利用堆这种数据结构设计的一种排序算法,它将待排序的序列构造成一个大顶堆,每次取出堆顶元素并调整堆,重复此过程直到所有元素排序完成。堆排序的时间复杂度为O(nlogn),是一种比较高效的排序方法。 选择...
本文将深入探讨五种常用的排序算法:快速排序、归并排序、选择排序、谢尔排序和堆排序。 **快速排序** 是由C.A.R. Hoare在1960年提出的,是一种效率较高的分治策略。其基本思想是通过一趟排序将待排序的数据分割成...
7. 堆排序:利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子节点的键值或索引总是小于(或者大于)它的父节点。堆排序具有不稳定性和时间复杂度为O(nlogn)的...
在计算机科学领域,排序算法是数据结构与算法中不可或缺的一部分,它们用于对一组数据进行排列,使得数据按照特定的顺序(通常为升序或降序)进行组织。本主题涵盖了六种经典的排序算法:希尔排序、堆排序、快速排序...
以下是关于"冒泡排序,选择排序,插入排序,希尔排序,堆排序,归并排序,快速排序"这七种常见排序算法的源码实现及相关知识点的详细解释: 1. **冒泡排序**:冒泡排序是一种简单的排序算法,它重复地遍历待排序的...
下面将详细讲解这7种排序算法:快速排序、归并排序、插入排序、选择排序、冒泡排序、堆排序以及希尔排序。 1. **快速排序**:由C.A.R. Hoare提出的,采用分治策略。基本思想是选取一个基准元素,通过一趟排序将待...
本资源聚焦于Python语言实现的各种排序算法,包括冒泡排序、选择排序、插入排序、希尔排序、归并排序、快速排序以及堆排序。下面将详细解释这些排序算法的工作原理及其在Python中的实现。 1. **冒泡排序(Bubble ...
排序算法java版,速度排行:冒泡排序、简单选择排序、直接插入排序、折半插入排序、希尔排序、堆排序、归并排序、快速排序.mht