[翻译]AGG 之适应性细分法描画贝塞尔曲线（下）

<<<< 续上文

 

Collinear Case

感谢 Timothee Groleau, http://www.timotheegroleau.com 里有他的方法，可以很简单地估计出曲率。就是点1234和线1-4的中点之间的距离。这与估算点和线之间的距离完全不同。他的方法清寒给出一个近似的值，虽然这个值仍然不够。但他的方法有一个很重要的优点，即，可以处理下面这种同线的情况。当四个点的顺序是下面这样的时候：

2--------1---------4----------3

 

所有使用点到线距离的判定方法在这种情况下都会失效。这里只有一条线段1-4 ，而这明显是不对的。Timothee 的判定方法在这种情况下仍然有效，这样我们就有了一个检测共线情况的机制。因此，处理共线情况的代码就相当简单了：

. . .
else
{
    // Collinear case
    //-----------------
    dx = x1234 - (x1 + x4) / 2;
    dy = y1234 - (y1 + y4) / 2;
    if(dx*dx + dy*dy <= m_distance_tolerance)
    {
        m_points.add(point_type(x1234, y1234));
        return;
    }
}

 

唯一要做的事就是要强制进行一次细分，因为可能会有上面提到过的“Z”型的情况。

嗯，伪代码如下：

void recursive_bezier(double x1, double y1, 
                      double x2, double y2, 
                      double x3, double y3, 
                      double x4, double y4,
                      unsigned level)
{
    double x12   = (x1 + x2) / 2;
    double y12   = (y1 + y2) / 2;
    double x23   = (x2 + x3) / 2;
    double y23   = (y2 + y3) / 2;
    double x34   = (x3 + x4) / 2;
    double y34   = (y3 + y4) / 2;
    double x123  = (x12 + x23) / 2;
    double y123  = (y12 + y23) / 2;
    double x234  = (x23 + x34) / 2;
    double y234  = (y23 + y34) / 2;
    double x1234 = (x123 + x234) / 2;
    double y1234 = (y123 + y234) / 2; 
   
    if(level)
    {
        if(curve_is_flat)
        {
            draw_line(x1, y1, x4, y4);
            return;
        }
    } 
    recursive_bezier(x1, y1, x12, y12, x123, y123, x1234, y1234, level + 1); 
    recursive_bezier(x1234, y1234, x234, y234, x34, y34, x4, y4, level + 1); 
}

也可以对递归进行限制，当然，这里看起来已经不必要去限制它了（因为已经有其它的判定方法来停止递归），但是严格的数学证明对我来说非常困难，所以，我直接把递归限定在 32 次以内。在实践中，即使是最恶劣的情况下（非常长的曲线，几千个点，很小的错误，有尖端点），我也没见过超过17次的递归，

Timothee 的判定方法在另一种共线情况下会产生很多的点： 1---2---3-------4 。 如果先检测出这种情况可能会比较，这样就只需要产生两个点（1-4），但我觉得这无关紧要，因为严格共线的情况非常少。所以，实际上这并不会影响性能。

还有另外两种共线的情况：

if(d2 > curve_collinearity_epsilon)
{
    // p1,p3,p4 are collinear (or coincide), p2 is considerable
    . . .
}
else if(d3 > curve_collinearity_epsilon)
{
    // p1,p2,p4 are collinear (or coincide), p3 is considerable
    . . .
}

 

那很简单，我们只是把点1和点3看起重合（点2和点4是第二种情况）。嗯，这里还有一个细节我想告诉你。

The Full Code

最后，我们看起完整的代码：

//------------------------------------------------------------------------
void curve4_div::init(double x1, double y1, 
                      double x2, double y2, 
                      double x3, double y3,
                      double x4, double y4)
{
    m_points.remove_all();
    m_distance_tolerance = 0.5 / m_approximation_scale;
    m_distance_tolerance *= m_distance_tolerance;
    bezier(x1, y1, x2, y2, x3, y3, x4, y4);
    m_count = 0;
} 

//------------------------------------------------------------------------
void curve4_div::recursive_bezier(double x1, double y1, 
                                  double x2, double y2, 
                                  double x3, double y3, 
                                  double x4, double y4,
                                  unsigned level)
{
    if(level > curve_recursion_limit) 
    {
        return;
    } 
    // Calculate all the mid-points of the line segments
    //----------------------
    double x12   = (x1 + x2) / 2;
    double y12   = (y1 + y2) / 2;
    double x23   = (x2 + x3) / 2;
    double y23   = (y2 + y3) / 2;
    double x34   = (x3 + x4) / 2;
    double y34   = (y3 + y4) / 2;
    double x123  = (x12 + x23) / 2;
    double y123  = (y12 + y23) / 2;
    double x234  = (x23 + x34) / 2;
    double y234  = (y23 + y34) / 2;
    double x1234 = (x123 + x234) / 2;
    double y1234 = (y123 + y234) / 2; 
    if(level > 0) // Enforce subdivision first time
    {
        // Try to approximate the full cubic curve by a single straight line
        //------------------
        double dx = x4-x1;
        double dy = y4-y1; 
        double d2 = fabs(((x2 - x4) * dy - (y2 - y4) * dx));
        double d3 = fabs(((x3 - x4) * dy - (y3 - y4) * dx)); 
        double da1, da2; 
        if(d2 > curve_collinearity_epsilon && d3 > curve_collinearity_epsilon)
        { 
            // Regular care
            //-----------------
            if((d2 + d3)*(d2 + d3) <= m_distance_tolerance * (dx*dx + dy*dy))
            {
                // If the curvature doesn't exceed the distance_tolerance value
                // we tend to finish subdivisions.
                //----------------------
                if(m_angle_tolerance < curve_angle_tolerance_epsilon)
                {
                    m_points.add(point_type(x1234, y1234));
                    return;
                } 
                // Angle & Cusp Condition
                //----------------------
                double a23 = atan2(y3 - y2, x3 - x2);
                da1 = fabs(a23 - atan2(y2 - y1, x2 - x1));
                da2 = fabs(atan2(y4 - y3, x4 - x3) - a23);
                if(da1 >= pi) da1 = 2*pi - da1;
                if(da2 >= pi) da2 = 2*pi - da2; 
                if(da1 + da2 < m_angle_tolerance)
                {
                    // Finally we can stop the recursion
                    //----------------------
                    m_points.add(point_type(x1234, y1234));
                    return;
                } 
                if(m_cusp_limit != 0.0)
                {
                    if(da1 > m_cusp_limit)
                    {
                        m_points.add(point_type(x2, y2));
                        return;
                    } 
                    if(da2 > m_cusp_limit)
                    {
                        m_points.add(point_type(x3, y3));
                        return;
                    }
                }
            }
        }
        else
        {
            if(d2 > curve_collinearity_epsilon)
            {
                // p1,p3,p4 are collinear, p2 is considerable
                //----------------------
                if(d2 * d2 <= m_distance_tolerance * (dx*dx + dy*dy))
                {
                    if(m_angle_tolerance < curve_angle_tolerance_epsilon)
                    {
                        m_points.add(point_type(x1234, y1234));
                        return;
                    } 
                    // Angle Condition
                    //----------------------
                    da1 = fabs(atan2(y3 - y2, x3 - x2) - atan2(y2 - y1, x2 - x1));
                    if(da1 >= pi) da1 = 2*pi - da1; 
                    if(da1 < m_angle_tolerance)
                    {
                        m_points.add(point_type(x2, y2));
                        m_points.add(point_type(x3, y3));
                        return;
                    } 
                    if(m_cusp_limit != 0.0)
                    {
                        if(da1 > m_cusp_limit)
                        {
                            m_points.add(point_type(x2, y2));
                            return;
                        }
                    }
                }
            }
            else
                if(d3 > curve_collinearity_epsilon)
                {
                    // p1,p2,p4 are collinear, p3 is considerable
                    //----------------------
                    if(d3 * d3 <= m_distance_tolerance * (dx*dx + dy*dy))
                    {
                        if(m_angle_tolerance < curve_angle_tolerance_epsilon)
                        {
                            m_points.add(point_type(x1234, y1234));
                            return;
                        } 
                        // Angle Condition
                        //----------------------
                        da1 = fabs(atan2(y4 - y3, x4 - x3) - atan2(y3 - y2, x3 - x2));
                        if(da1 >= pi) da1 = 2*pi - da1; 
                        if(da1 < m_angle_tolerance)
                        {
                            m_points.add(point_type(x2, y2));
                            m_points.add(point_type(x3, y3));
                            return;
                        } 
                        if(m_cusp_limit != 0.0)
                        {
                            if(da1 > m_cusp_limit)
                            {
                                m_points.add(point_type(x3, y3));
                                return;
                            }
                        }
                    }
                }
                else
                {
                    // Collinear case
                    //-----------------
                    dx = x1234 - (x1 + x4) / 2;
                    dy = y1234 - (y1 + y4) / 2;
                    if(dx*dx + dy*dy <= m_distance_tolerance)
                    {
                        m_points.add(point_type(x1234, y1234));
                        return;
                    }
                }
        }
    } 
    // Continue subdivision
    //----------------------
    recursive_bezier(x1, y1, x12, y12, x123, y123, x1234, y1234, level + 1); 
    recursive_bezier(x1234, y1234, x234, y234, x34, y34, x4, y4, level + 1); 
} 
//------------------------------------------------------------------------
void curve4_div::bezier(double x1, double y1, 
                        double x2, double y2, 
                        double x3, double y3, 
                        double x4, double y4)
{
    m_points.add(point_type(x1, y1));
    recursive_bezier(x1, y1, x2, y2, x3, y3, x4, y4, 0);
    m_points.add(point_type(x4, y4));
}

 

老实说其实这还不是完整的代码，不过这里已经展示了整个算法。余下的部分（类的定义之类的）可以在下面几个文件中找到：

Class curve4_div, files agg_curves.h, agg_curves.cpp.

上面我说要告诉你的那个细节是关于处理共线情况的一段代码：

if(da1 < m_angle_tolerance)
{
    m_points.add(point_type(x2, y2));
    m_points.add(point_type(x3, y3));
    return;
}

 

你可以看到，我使用了两个点，而不是一个点（1234）。我也是通过实验得来的。只加一个点会在尖端点产生错误的角度。我不知道数学上这是怎么回事，不过，反正它是 OK 的。

这个类有下面的这些参数：

• -approximation_scale ：最终决定估算的精度。在实际应用中，我们需要从点的世界坐标转换到屏幕坐标，因此总会存在一定的缩放因子。曲线通常是在世界坐标系中处理的，而进行估算时又要转换为像素值。一般看起来会是这样的：m_curved.approximation_scale(m_transform.scale());
  这里，m_transform 是一个仿型映射的矩阵，里面包含了所有的转换，包括视点和缩放。
• -angle_tolerance：以弧度来设置。这个值越少，在曲线的转弯处的估算就越精确。不过，如果设置为0，那么表示完全 不考虑角度条件。
• -cusp_limit：一个以弧度来设置的角度。如果是0，那么只有真正的尖端(cusp)才会有 bevel cut。如果大于0，那么它会限制曲线的弯曲度，值越大，曲线锐利的转弯处被切得就越少。一般，这个值不应该大于10-15度。

我上面提到过，通过角度来进行估算开销比较大，而且我们也不是总是需要它。我们只是在有曲线有明显的stroke或是contours的时候才用它。所以，为了优化它，我们可以这样做：

double scl = m_transform.scale();
m_curved.approximation_scale(scl); 
// Turn off processing of curve cusps
//-----------------
m_curved.angle_tolerance(0); 
if(attr.fill_flag)
{
    // Process the fill
    . . .
} 
if(attr.stroke_flag)
{
    // Process the stroke
    //---------------------
    // If the *visual* line width is considerable we 
    // turn on processing of sharp turns and cusps.
    //---------------------
    if(attr.stroke_width * scl > 1.0)
    {
        m_curved.angle_tolerance(0.2);
    }
    . . .
}

 

这会提升整体的速度。

Quadric Curves

二次曲线处理起来要简单的得多。我们连 cusp_limit 的判定都不需要，因为共线的情况已经可以处理所有退化的情况：

//------------------------------------------------------------------------
void curve3_div::init(double x1, double y1, 
                      double x2, double y2, 
                      double x3, double y3)
{
    m_points.remove_all();
    m_distance_tolerance = 0.5 / m_approximation_scale;
    m_distance_tolerance *= m_distance_tolerance;
    bezier(x1, y1, x2, y2, x3, y3);
    m_count = 0;
} 
//------------------------------------------------------------------------
void curve3_div::recursive_bezier(double x1, double y1, 
                                  double x2, double y2, 
                                  double x3, double y3,
                                  unsigned level)
{
    if(level > curve_recursion_limit) 
    {
        return;
    } 
    // Calculate all the mid-points of the line segments
    //----------------------
    double x12   = (x1 + x2) / 2;                
    double y12   = (y1 + y2) / 2;
    double x23   = (x2 + x3) / 2;
    double y23   = (y2 + y3) / 2;
    double x123  = (x12 + x23) / 2;
    double y123  = (y12 + y23) / 2; 
    double dx = x3-x1;
    double dy = y3-y1;
    double d = fabs(((x2 - x3) * dy - (y2 - y3) * dx)); 
    if(d > curve_collinearity_epsilon)
    { 
        // Regular care
        //-----------------
        if(d * d <= m_distance_tolerance * (dx*dx + dy*dy))
        {
            // If the curvature doesn't exceed the distance_tolerance value
            // we tend to finish subdivisions.
            //----------------------
            if(m_angle_tolerance < curve_angle_tolerance_epsilon)
            {
                m_points.add(point_type(x123, y123));
                return;
            } 
            // Angle & Cusp Condition
            //----------------------
            double da = fabs(atan2(y3 - y2, x3 - x2) - atan2(y2 - y1, x2 - x1));
            if(da >= pi) da = 2*pi - da; 
            if(da < m_angle_tolerance)
            {
                // Finally we can stop the recursion
                //----------------------
                m_points.add(point_type(x123, y123));
                return;                 
            }
        }
    }
    else
    {
        // Collinear case
        //-----------------
        dx = x123 - (x1 + x3) / 2;
        dy = y123 - (y1 + y3) / 2;
        if(dx*dx + dy*dy <= m_distance_tolerance)
        {
            m_points.add(point_type(x123, y123));
            return;
        }
    } 
    // Continue subdivision
    //----------------------
    recursive_bezier(x1, y1, x12, y12, x123, y123, level + 1); 
    recursive_bezier(x123, y123, x23, y23, x3, y3, level + 1); 
} 
//------------------------------------------------------------------------
void curve3_div::bezier(double x1, double y1, 
                        double x2, double y2, 
                        double x3, double y3)
{
    m_points.add(point_type(x1, y1));
    recursive_bezier(x1, y1, x2, y2, x3, y3, 0);
    m_points.add(point_type(x3, y3));
}

Demo Application

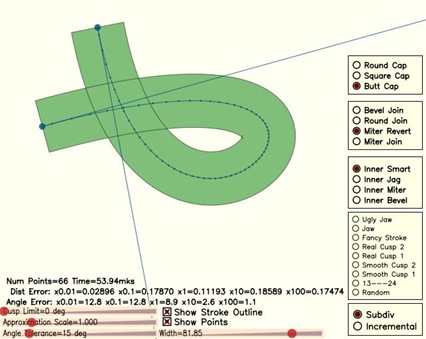
你可以从这里下载一个Win32下的Demo程序

载图如下：

 

这个程度运行起来很慢，不过这不重要。我使用五个缩放尺度计算了最大的距离和角度误差：0.01, 0.1, 1, 10, 和 100（这非常耗时）。距离误差是指设置approximation_scale() 为以上五个值中的一个，计算出最大误差，然后乘以 approximation_scale() 的值。所以，它是屏幕分辨率（像素值）归一化后的最大误差。（原句： So that, it will be the maximal error normalized to the screen resolution (pixels).）

参考曲线是用 Paul Bourke 方法画的，使用的是很小的步进（4096个点）。

你可以清楚地看到递增方法（incremental method）和细分方法（subdivision method）最大误差的差别。不管scale是多少，细分方法的误差基本保持了一致。但递增方法在 scale为10和100时误差变小了（But in the incremental method it decreases on the 10x and 100x scales.）。这种行为明显是不对的，因为我们不需要0.001像素的错误。这意味着曲线的点太多了。我们需要在误差和点数之间取得平衡。

你可以比较下两个渲染的结果：

• Incremental Tiger
• Subdivided Tiger

这个结果看起来差别很小，但是如果你把两张图下下来，使用滑动窗口来转换两张图。这两个例子中，我设置精度的目标是为了让两者产生的点的数目一相近。如果你仔细比较这两个图，你会发生细分方法渲染的结果要精确得多。

当然，递增方法也很好，因为它很简单，很快，可以用在那些性能要求很高的地方。一个典型的情形是，用于字体的渲染。字体通常没有多少复杂的曲线，所有的曲线都像弧线（TrueType字体大部分情况下只用了二次曲线）。

Update 1

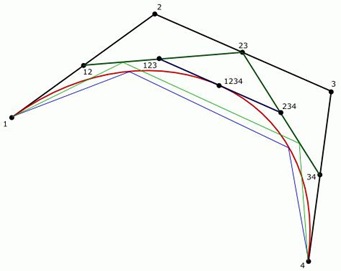
在写这篇文章的时候我已经意识到，添加点1234并不够好。In this case the curve is circumscribed and the polyline is escribed. 如果我们添加点23，我们可以得到更好的结果。假设我们只进行一次细分，比较一下两者的结果：

这里，蓝色的线是我们用点1234产生的，而绿色的则是使用点23产生的。很明显，绿色线的误差要小一些，在实际中，大约是1.5或2倍的差别。

Update 2

在 comp.graphics.algorithms 新闻组，我因为对专著的不熟悉而受到了相当严历的批评。完整的讨论在这里可以找到，你也可以使用“Adaptive Subdivision of Bezier Curves McSeem”在 http://groups.google.com 里进行搜索。 在网上可以很容易地找到一篇叫“Adaptive forward differencing for rendering curves and surfaces”的文章。里面介绍的方法很好，不过仍然不能解决平滑 stroke 中遇到的所有问题。

但最有意思是信息来自一个昵称是“Just d'FAQs”的人。下面是他的话：

一个很有名的曲线平坦度检测方法比你使用的方法要简单而且可靠。这种方法是基于这样的观察：如果曲线是一个点在端点到端点之间以匀速运动形成的，那么它的控制点会均匀地分布在两个端点之间。因此，我们计算偏移时应该使用中间控制的距离，而不是用线段的距离（原句：Therefore, our measure of how far we deviate from that ideal uses distance of the middle controls, not from the line itself, but from their ideal *arrangement*.）。点2应该是点1和点3的中点，点3应该是点2和点4的中点。（译注：这段把我弄晕了……）

这个方法仍然可以改进，因为我们可以消除距离检测中的平方根计算，可以保留Euclidean metric，但是taxicab metric会更快，而且一样安全。在这种度量方法中（taxicab metric），(x,y)的长度是：|x|+|y| 。

反应成代码就像下面这样：

if(fabs(x1 + x3 - x2 - x2) +
   fabs(y1 + y3 - y2 - y2) +
   fabs(x2 + x4 - x3 - x3) +
   fabs(y2 + y4 - y3 - y3) <= m_distance_tolerance_manhattan)
{
    m_points.add(point_type(x1234, y1234));
    return;
}

 

这种方法不需要强制进行第一次细分，而且在任何情况下都很健壮。作者坚持认为这种方法已经够好了，不过我经过一些额外的实验后发现，结果和递增方法有些类似。这种估算没有在点数和差误之间平衡好。但在共线的情况下很棒。我把它融合到我的代码中了，现在看起来，我可以停止这方面的研究了。这个方法需要几种不同的度量，“Manhattan”（或者叫“taxicab”），我们需要将 tolerance 像下面这样规范化：

m_distance_tolerance_square = 0.5 / m_approximation_scale;
m_distance_tolerance_square *= m_distance_tolerance_square;
m_distance_tolerance_manhattan = 4.0 / m_approximation_scale;

 

在共线的情况下，这种方法比Timothee Groleau的方法好。

完整的代码在这里: curve4_div, 文件：agg_curves.h, agg_curves.cpp.