[翻译] AGG 之贝塞尔插值

原文地址：http://www.antigrain.com/research/
bezier_interpolation/index.html#PAGE_BEZIER_INTERPOLATION

Interpolation with Bezier Curves  贝塞尔插值

A very simple method of smoothing polygons 一种非常简单的多边形平滑方法

翻译：唐风

之前 comp.graphic.algorithms 上有一个讨论，是关于怎么样使用曲线对多边形进行插值处理，使得最终产生的曲线是光滑的而且能通过所有的顶点。Gernot Hoffmann 建议说使用著名的 B-Spline 来进行插值。这里有他当时的文章。B-Spline 在这里效果很好，它看起来就像是一个固定在多边形顶点上的橡皮尺（elastic ruler）。

  

 

---

 

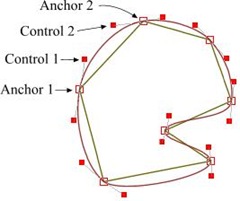但我有个大胆的推测，我觉得肯定还存在更简单的方法。比如，使用三次贝塞曲线(cubic Bezier)进行近似。贝塞尔曲线有两个固定点（起点和终点），另加两个决定曲线形状的控制点(CP）。关于贝塞尔曲线的更多知识可以在搜索引擎中找到，比如，你可以参考 Paul Bourke 的站点。现在给贝塞尔曲线的锚点（固定点），也就是多边形的某一对顶点，那么问题是，我们怎么计算控制点的位置？我运行 Xara X 然后画出了右边这个图形，这很简单，所以我决定尝试下计算出它们的坐标。很显然，多边形两条相邻边的两个控制点与这两个控制点之间的顶点应该在一条直线上，只有这样，两条相邻的插值曲线才能平滑地连接在一起。所以，这两个控制点应该是相对于顶点是对称的，不过，也不全是……，因为真正的对称就要求它们与中心点的距离应该是相等的，但对于我们的情况中并不完全是这样的。一开始，我试着先算出多边形两条边的角平分线，然后把控制点放在这条角平分线的垂直线上。但从图上可以看到，控制点的连线并不会总是垂直于角平分线的。

 

---

 

最终，我找到一个非常简单的办法，不需要任何复杂的数学计算。首先，我们计算出多边形所有边线的中点，Ai。

 

---

 

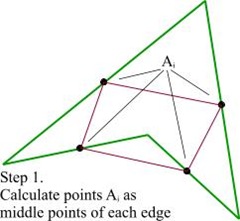
然后连接起相邻边中点，得到很多线段，记为 Ci 。并用图记的方法计算出 Bi 点。

 

---

 

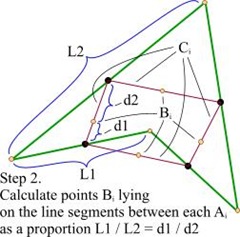
最后一步，只需要简单地将 Ci 进行平移，平移的路径就是每条线段上 Bi 到对应顶点的路径。就这样，我们计算出了贝塞尔曲线的控制点，平滑的结果看起来也很棒。

 

---

 

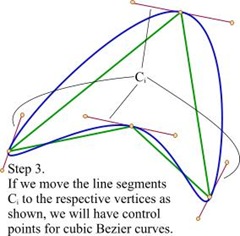
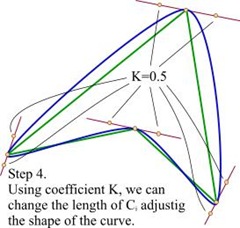
这里还可以做一点小小的改进，因为我们已经得到了一条决定控制点的直线，所以，我们可以根据需要，使控制点在这条直线上移动，这样可以改变插值曲线的状态。我使用了一个与控制点和顶点初始距离相关的系数 K ，用来沿直线移动控制点。控制点离顶点越远，图形看起来就越锐利。

 

---

 

下面是用原始形状和系统K=1.0的贝塞尔插值两种方法来描画的 SVG 的狮子。

 

 

---

 

下面是放大图

 

 

---

 

这个方法对于自相关的多边形也适用，下面的例子可以看到，结果非常有意思：

 

---

 

 

---

 

 

---

 

这个方法只是探索和经验式的，如果从严格的数学模型的角度看它可能是错误的。但在实际使用中的效果已经足够好了，而且这个方法只需要最小的计算量。下面的代码就是用来画出上面狮子图像的。这些代码并没有进行优化，只是用来演示的。里面有些变量计算了两次，在实际程序中，如果连续的步骤中都用到同一个变量值，我们可以先缓存变量值进行复用（以避免重复的计算）。

// Assume we need to calculate the control
// points between (x1,y1) and (x2,y2).
// Then x0,y0 - the previous vertex,
//      x3,y3 - the next one. 
double xc1 = (x0 + x1) / 2.0;
double yc1 = (y0 + y1) / 2.0;
double xc2 = (x1 + x2) / 2.0;
double yc2 = (y1 + y2) / 2.0;
double xc3 = (x2 + x3) / 2.0;
double yc3 = (y2 + y3) / 2.0; 
double len1 = sqrt((x1-x0) * (x1-x0) + (y1-y0) * (y1-y0));
double len2 = sqrt((x2-x1) * (x2-x1) + (y2-y1) * (y2-y1));
double len3 = sqrt((x3-x2) * (x3-x2) + (y3-y2) * (y3-y2)); 
double k1 = len1 / (len1 + len2);
double k2 = len2 / (len2 + len3); 
double xm1 = xc1 + (xc2 - xc1) * k1;
double ym1 = yc1 + (yc2 - yc1) * k1; 
double xm2 = xc2 + (xc3 - xc2) * k2;
double ym2 = yc2 + (yc3 - yc2) * k2; 
// Resulting control points. Here smooth_value is mentioned
// above coefficient K whose value should be in range [0...1].
ctrl1_x = xm1 + (xc2 - xm1) * smooth_value + x1 - xm1;
ctrl1_y = ym1 + (yc2 - ym1) * smooth_value + y1 - ym1; 
ctrl2_x = xm2 + (xc2 - xm2) * smooth_value + x2 - xm2;
ctrl2_y = ym2 + (yc2 - ym2) * smooth_value + y2 - ym2; 

使用三次贝塞尔近似的代码：

// Number of intermediate points between two source ones,
// Actually, this value should be calculated in some way,
// Obviously, depending on the real length of the curve.
// But I don't know any elegant and fast solution for this
// problem.
#define NUM_STEPS 20 
void curve4(Polygon* p,
            double x1, double y1,   //Anchor1
            double x2, double y2,   //Control1
            double x3, double y3,   //Control2
            double x4, double y4)   //Anchor2
{
    double dx1 = x2 - x1;
    double dy1 = y2 - y1;
    double dx2 = x3 - x2;
    double dy2 = y3 - y2;
    double dx3 = x4 - x3;
    double dy3 = y4 - y3; 
    double subdiv_step  = 1.0 / (NUM_STEPS + 1);
    double subdiv_step2 = subdiv_step*subdiv_step;
    double subdiv_step3 = subdiv_step*subdiv_step*subdiv_step; 
    double pre1 = 3.0 * subdiv_step;
    double pre2 = 3.0 * subdiv_step2;
    double pre4 = 6.0 * subdiv_step2;
    double pre5 = 6.0 * subdiv_step3; 

    double tmp1x = x1 - x2 * 2.0 + x3;
    double tmp1y = y1 - y2 * 2.0 + y3; 
    double tmp2x = (x2 - x3)*3.0 - x1 + x4;
    double tmp2y = (y2 - y3)*3.0 - y1 + y4; 
    double fx = x1;
    double fy = y1; 
    double dfx = (x2 - x1)*pre1 + tmp1x*pre2 + tmp2x*subdiv_step3;
    double dfy = (y2 - y1)*pre1 + tmp1y*pre2 + tmp2y*subdiv_step3; 
    double ddfx = tmp1x*pre4 + tmp2x*pre5;
    double ddfy = tmp1y*pre4 + tmp2y*pre5; 
    double dddfx = tmp2x*pre5;
    double dddfy = tmp2y*pre5; 
    int step = NUM_STEPS; 
    // Suppose, we have some abstract object Polygon which
    // has method AddVertex(x, y), similar to LineTo in
    // many graphical APIs.
    // Note, that the loop has only operation add!
    while(step--)
    {
        fx   += dfx;
        fy   += dfy;
        dfx  += ddfx;
        dfy  += ddfy;
        ddfx += dddfx;
        ddfy += dddfy;
        p->AddVertex(fx, fy);
    }
    p->AddVertex(x4, y4); // Last step must go exactly to x4, y4
}

你可以下载一个能运行的画狮子的例子，对它进行旋转和缩放，也可以生成一些随机的多边形。点左键并拖动它可以围绕中心点旋转和缩放图像。点右键并从左向右拖动，可以改变系统数K。 K＝1时大约是距窗口左边100像素处。每次双击会产生一个随机的多边形，对于这些多边形，也可以进行旋转、缩放以及改变K值的操作。

评论

1 楼 westice 2010-08-23  

非常好！正苦于怎么确定贝塞尔曲线的控制点，很好的思路。