Beringei高性能时间序列内存数据库原理

时间戳压缩算法

 

1. 首先普通的时间戳如下：

2017年3月3日 3：00：00   1488481200
2017年3月3日 3：01：02   1488481262
2017年3月3日 3：02：02   1488481322
2017年3月3日 3：03：02   1488481382

秒级别的时间戳用long类型存储需要占用8bytes。 如果直接存储以上数据需要32个bytes(256 bits).

2. 最简单的优化自然是存储差值 Delta = T(n)-T(n-1) ， 这个时候需要引入一个起始时间戳和Delta阈值，比如：起始时间为3：00：00，阈值为2个小时。以下为阀值之内的位点数：

时间戳 unix格式 Delta

2017年3月3日 3：00：00	1488481200	0
2017年3月3日 3：01：02	1488481262	62
2017年3月3日 3：02：02	1488481322	60
2017年3月3日 3：03：02	1488481382	60

**每个Delta数值的范围从long.MAX缩小到(0~7200)用13个bit就可以存储。因此存储以上数据需要103bits(64+ 13*3 ) **

3. 再进一步,如果存储差值的差值呢delta-of-delta（本文中用D表示）? 我们来看一下效果:

时间戳 unix格式 Delta Delta of Delta

2017年3月3日 3：00：00	1488481200	0	0
2017年3月3日 3：01：02	1488481262	62	62
2017年3月3日 3：02：02	1488481322	60	-2
2017年3月3日 3：03：02	1488481382	60	0

 

 

 

数值的范围变得很小了，并且可以进行压缩，根据以下压缩算法

// '0' = delta of delta did not change
// '10' followed by a value length of 7
// '110' followed by a value length of 9
// '1110' followed by a value length of 12
// '1111' followed by a value length of 32

D 范围 标识位 D数值位数bits 总位数bits

0	0(1bits)	0	1
[-63,64]	10(2bits)	7	9
[-255,256]	110(3bits)	9	12
[-2047,2048]	1110(4bits)	12	16
大于2048	1111(4bits)	32	36

• 起始时间戳需要64bits，
• “2017年3月3日 03:01:02”的D值为62，所以标识位是10，7个数值位，总共9个bits.
• "2017年3月3日 03:03:02"的D值为0， 标识位0，共需要1个bit

采用压缩算法后只需要64+9+9+1=73个bits存储。

时间戳 Delta Delta of Delta 压缩后位数

2017年3月3日 3：00：00	/	/	/
2017年3月3日 3：01：02	62	62	9
2017年3月3日 3：02：02	60	-2	9
2017年3月3日 3：03：02	60	0	1

结论：4个时间戳（32bytes），通过delta，再通过delta-of-delta算法，从32个bytes(256 bits)，到103bits，再到73bits，整体的压缩比为：3.5；

 

 

数值压缩算法：

看完了时间戳的压缩，我们再来看一下数值的压缩。类似于时间戳Delta, 数值采用的是异或而不是差值。

可以看这里的转换工具

整数 Double 精度十六进制

12	0x4028000000000000
24	0x4038000000000000
15	0x402E000000000000
12	0x4028000000000000
35	0x4041800000000000

---

浮点数 Double 精度十六进制

15.5	0x402F000000000000
14.0625	0x402C200000000000
3.25	0x400A000000000000
8.625	0x4021400000000000

---

以浮点数为例采用XOR运算后：

浮点数 Double 精度十六进制 XOR

15.5	0x402F000000000000
14.0625	0x402C200000000000	0x0003200000000000
3.25	0x400A000000000000	0x0026200000000000
8.625	0x4021400000000000	0x002b400000000000

XOR后的数值压缩有众多算法可以选择，比如gzip, 7zip等等。

“Fast Lossless Compression of Scientific Floating-Point Data”这篇论文提出了DFCM压缩算法。并且从压缩率，压缩/解压效率方面与一些通用压缩算法进行了评测，如下：

 

 

 

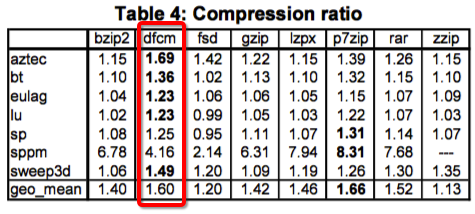
相比gzip，DFCM的压缩速度和压缩率都要更胜一筹。

参考浮点数无损压缩算法DFCM：

 

 

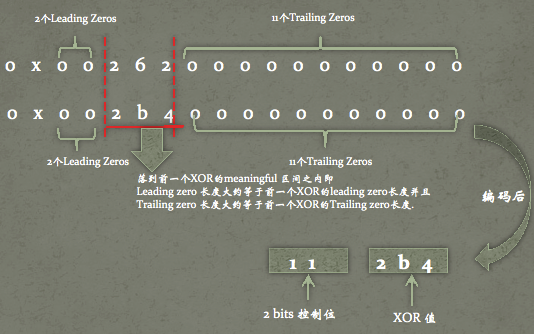
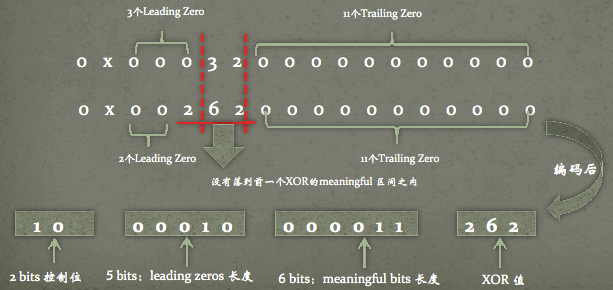
XOR的值可以按照leading zero, meaningful bits, trailing zeros 划分。

• Leading Zeros: 就是XOR后非零数值前面零的个数
• Trailing Zeros: 就是XOR后非零数值后面零的个数
• Meaningful Bits: 中间非零的个数

 

划分后，对DFCM简化，预测算子采用前一个XOR的值，编码规则如下：

• 第一个值不压缩
• XOR后的数据计算控制位,如下:
  • 如果XOR是0, 存储一个bit 0。
  • 如果XOR不是0，控制位第一个bit设置1，第二个bit以及随后的数据按照以下方式计算：
  • meaningful bits落在了前一个XOR的meaningful bits区域内，控制位的第二个bit为1，接下来是XOR数值.

• 否则控制位的第二个bit为0 ．并且接下来存放:
  • 5 bits: Leading bits 个数
  • 6 bits: Meaningful bits 个数
  • 随后放置数值

数据由原来的256bits压缩到117bits

浮点数 压缩后 XOR值

15.5	无压缩	/
14.0625	13bits(头部控制位)+5bits(实际数值）	0x0003200000000000
3.25	13bits(头部控制位)+10bits(实际数值）	0x0026200000000000
8.625	2bits(头部控制位)+10bits(实际数值)	0x002b400000000000

 

参考：

https://yq.aliyun.com/articles/69354?spm=5176.8278999.602941.2