Given an integer n, return the number of trailing zeroes in n!.
Note: Your solution should be in logarithmic time complexity.
这个要用到数学知识了。参见Wikipedia-Trailing Zeroes。
The number of trailing zeros in the decimal representation of n!, the factorial of a non-negative integer n, is simply the multiplicity of the primefactor 5 in n!. This can be determined with this special case of de Polignac's formula:[1]

where k must be chosen such that

and 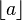 denotes the floor function applied to a. For n = 0, 1, 2, ... this is
denotes the floor function applied to a. For n = 0, 1, 2, ... this is
For example, 53 > 32, and therefore 32! = 263130836933693530167218012160000000 ends in

zeros. If n < 5, the inequality is satisfied by k = 0; in that case the sum is empty, giving the answer 0.
Solution:
public int trailingZeroes(int n) {
int count = 0;
while(n>=5) {
n /= 5;
count += n;
}
return count;
}







相关推荐
javascript js_leetcode题解之172-factorial-trailing-zeroes.js
《在IDE中高效进行LeetCode练习:leetcode-editor的深度解析》 在编程学习与技能提升的过程中,LeetCode作为一款广受欢迎的在线编程挑战平台,帮助众多开发者锻炼算法思维,提高编程能力。而为了进一步提升练习体验...
leetcode-cli-plugins leetcode-cli 的第 3 方插件。 什么是 如何使用 如何使用 插件 名称 描述 增强的命令 按公司或标签过滤问题 list 不要在同一台计算机上使 Chrome 的会话过期 login 不要在同一台计算机上使 ...
leetcode-习题集资源leetcode-习题集资源leetcode-习题集资源leetcode-习题集资源leetcode-习题集资源leetcode-习题集资源
在IDE中解决LeetCode问题,支持leetcode.com与leetcode-cn.com,满足基本的做题需求。 理论上支持: IntelliJ IDEA PhpStorm WebStorm PyCharm RubyMine AppCode CLion GoLand DataGrip Rider MPS Android Studio。
LeetCode Editor 7.4 版本的下载是一个名为 "leetcode-editor" 的压缩包文件。这个压缩包的导入过程非常简单,只需要将它直接拖入 IDEA 界面,IDEA 会自动识别并安装插件。这种方式使得安装过程无需额外的步骤,对于...
leetcode-习题集资源源代码leetcode-习题集资源源代码leetcode-习题集资源源代码leetcode-习题集资源源代码leetcode-习题集资源源代码
~/.vscode/extensions/leetcode.vscode-leetcode-0.17.0/node_modules/vsc-leetcode-cli/bin/leetcode /usr/local/bin/leetcode 修改模板 open ~/.vscode/extensions/leetcode.vscode-leetcode-0.17.0/node_modules/...
解题思路思路和LeetCode-python 503.下一个更大元素 II一致,只是这里求的是下标的距离,而不是数值倒序搜索,用到栈,栈里存储索引情况1:若栈为
《PyPI官网下载 | leetcode-export-1.1.tar.gz》 在编程世界里,LeetCode是一个备受程序员喜爱的在线平台,它提供了大量的算法题目,帮助开发者提升编程技能和解决问题的能力。而Python作为一门广泛使用的高级编程...
leetcode-cheat 的发布 它是什么 ? 这是一个chrome 扩展,可以帮助您更高效地使用 leetcode。您可以从 重要: leetcode-cheat 现在只支持中文版。 也就是说不完全支持leetcode.com,但是你可以用leetcode-cn.com代替...
leetcode-cli 一个享受 leetcode 的高效 cli 工具! 非常感谢 leetcode.com,一个非常棒的网站! ⦙⦙⦙⦙⦙⦙⦙⦙ 一个很打问题的方法。 问题来缓解离线思考。 编码前的源代码。 居住和与 leetcode.com。 下载你...
`swift-Swif-LeetCode-Utils` 是一个实用工具库,它为Swift程序员提供了方便快捷的方法来处理这些问题。这个项目可以帮助你更高效地进行LeetCode上的编程练习,提升你的解决方案的可读性和简洁性。 首先,让我们...
java java_leetcode-115-distinct-subsquences
java java_leetcode-112-path-sum
java java_leetcode-101-symmetric-tree
java java_leetcode-100-same-tree
然后进入到LeetCode-Spider目录中修改config.json,其中outputDir需要填写该工程的/docs/views文件夹路径 { "username": "aaa", "password": "bbb", "outputDir": "/Users/liuyao/Downloads/LeetCode-Blog-Test/docs...
970. 强整数对数运算function powerfulIntegers(x: number, y: number, bound: number): numb