纯Shading Language绘制HTML5时钟

今天是2014年的最后一天，这个时刻总会让人想起时钟，再过几个小时地球人都要再老了一岁，于是搞个HTML5版的时钟就是我们今天要完成的任务，实现HTML5的时钟绘制一般会采用三种方式，第一种采用CSS的实现方式，例如 http://www.css-tricks.com/examples/CSS3Clock/ ；第二种采用SVG的实现方式，例如 http://www.css-tricks.com/examples/CSS3Clock/；第三种采用Cavnas的2D绘制方式，如HT for Web中《矢量手册》中自定义绘制的clock例子，HT的例子的实现效果如下，其实现代码附在本文的最后部分。

以上三种方式都是较容易理解的实现方式，今天我们将采用的则是较为少见的WebGL纯Shading Language实现方式，这种方式极其高效，毕竟我们采用的是可利用GPU硬件加速的WebGL技术，CPU代码角度看仅有两个三角形的绘制，真正表盘的绘制逻辑完全在GPU对两个三角形进行Fragment Shading时实现。

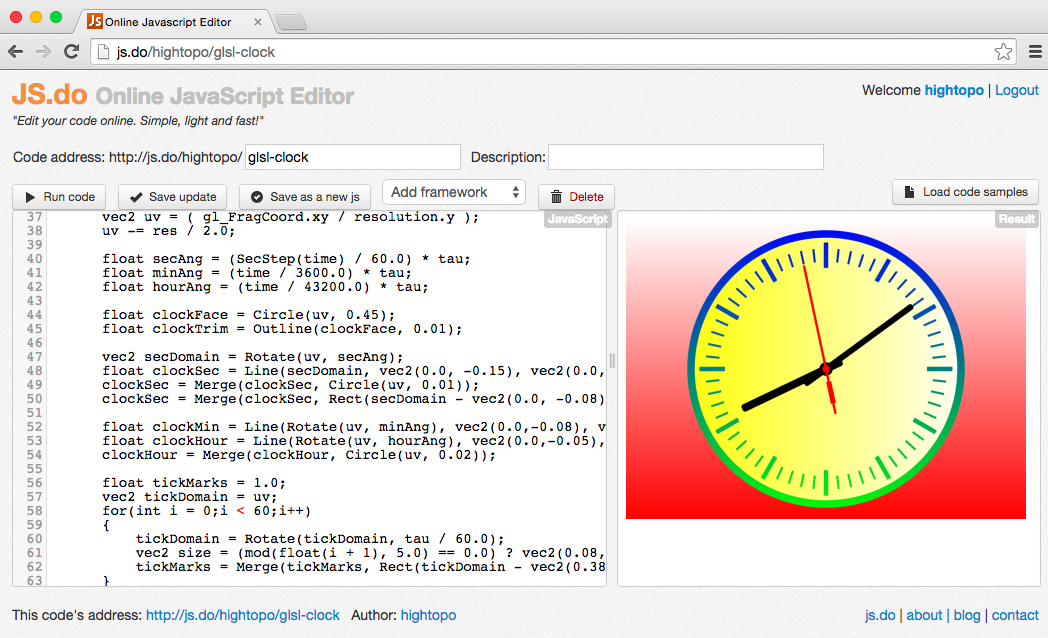
可通过这里 http://js.do/hightopo/glsl-clock 玩玩最后的实现效果以及实现代码，采用GLSL的实现最重要的就是决定当前坐标位置的gl_FragColor的颜色，我们将始终分为表盘、外圈、刻度、时针、分针和秒针几个部分，代码后部分的留个连续Blend代码相当于逐层绘制的逻辑，以下几个函数技术点说明：

• Rect函数中的clamp(uv, -size/2.0, size/2.0))是我们决定点是否在矩形区域的技巧
• 函数Rotate(vec2 uv,float angle)将坐标点旋转到水平或垂直位置方便我们确定Rect和Line参数进行对比
• Blend函数mix(shapeColor, backColor, smoothstep(0.0, 0.005, shape))是常用的混合mix和smoothstep达到更好处理边缘平滑效果GLSL常用技巧

为了说明mix和smoothstep的融合效果，我搞了个 http://js.do/hightopo/glsl-smooth-clrcle 的例子，你可以尝试去掉#define SMOOTH后边缘锯齿较明显的问题，也可以调节smoothstep(0.49, 0.5, d)的0.49为0.3等较小的参数体验渐进的效果，以下为几种效果的综合对比

GLSL的Fragment Shader实现代码如下：

#ifdef GL_ES
precision mediump float;
#endif

uniform float time;
uniform vec2 resolution;

float pi = 3.1415926; 
float tau = pi * 2.0;

vec2 Rotate(vec2 uv,float angle);

float Circle(vec2 uv,float r);
float Rect(vec2 uv,vec2 size,float r);
float Line(vec2 uv,vec2 start,vec2 end,float r);
float Merge(float a,float b);
float Outline(float a,float r);

vec3 Blend(vec3 backColor, vec3 shapeColor, float shape);

float SecStep(float x); 

void main( void ) 
{
		vec2 res = resolution / resolution.y;
		vec2 uv = ( gl_FragCoord.xy / resolution.y );
		uv -= res / 2.0;                                       

		float secAng = (SecStep(time) / 60.0) * tau;
		float minAng = (time / 3600.0) * tau;
		float hourAng = (time / 43200.0) * tau;

		float clockFace = Circle(uv, 0.45);
		float clockTrim = Outline(clockFace, 0.01);

		vec2 secDomain = Rotate(uv, secAng); 
		float clockSec = Line(secDomain, vec2(0.0, -0.15), vec2(0.0, 0.35), 0.001);
		clockSec = Merge(clockSec, Circle(uv, 0.01));
		clockSec = Merge(clockSec, Rect(secDomain - vec2(0.0, -0.08), vec2(0.012, 0.07), 0.0));

		float clockMin = Line(Rotate(uv, minAng), vec2(0.0,-0.08), vec2(0.0, 0.35), 0.005);
		float clockHour = Line(Rotate(uv, hourAng), vec2(0.0,-0.05), vec2(0.0,0.3), 0.007);
		clockHour = Merge(clockHour, Circle(uv, 0.02));

		float tickMarks = 1.0;
		vec2 tickDomain = uv;
		for(int i = 0;i < 60;i++)
		{
			tickDomain = Rotate(tickDomain, tau / 60.0);
			vec2 size = (mod(float(i + 1), 5.0) == 0.0) ? vec2(0.08, 0.01) : vec2(0.04, 0.002); 
			tickMarks = Merge(tickMarks, Rect(tickDomain - vec2(0.38, 0.0), size, 0.0));
		}

		vec3 faceColor = mix(vec3(1.0, 1.0, 0.0), vec3(1.0, 1.0, 1.0), uv.x+0.5); 
		vec3 trimColor = mix(vec3(0.0, 1.0, 0.0), vec3(0.0, 0.0, 1.0), uv.y + 0.5); 
		vec3 secColor = vec3(1.0, 0.0, 0.0); 
		vec3 handColor = vec3(0.0, 0.0, 0.0);

		vec3 color = mix(vec3(1.0, 0.0, 0.0), vec3(1.0, 1.0, 1.0), uv.y+0.5);
		color = Blend(color, faceColor, clockFace);
		color = Blend(color, trimColor, clockTrim);
		color = Blend(color, trimColor, tickMarks);                    
		color = Blend(color, handColor, clockHour);
		color = Blend(color, handColor, clockMin);
		color = Blend(color, secColor, clockSec);	

		gl_FragColor = vec4(color, 1.0);
}
float SecStep(float x)
{
	float interp = smoothstep(0.80, 1.0, mod(x, 1.0));
	return floor(x) + interp + (sin(interp * pi)) ;
}            
float Line(vec2 uv,vec2 start,vec2 end,float r)
{
	return Rect(uv-(end+start)/2.0, vec2(r, end.y - start.y), r);
}
float Rect(vec2 uv,vec2 size,float r)
{
	return length(uv - clamp(uv, -size/2.0, size/2.0)) - r;	
}            
vec2 Rotate(vec2 uv,float angle)
{
	return mat2(cos(angle), sin(angle),-sin(angle), cos(angle)) * uv;
}
float Circle(vec2 uv,float r)
{
	return length(uv) - r;	
}
float Merge(float a,float b)
{
	return min(a, b);	
}
float Outline(float a,float r)
{
	return abs(a) - r;	
}
vec3 Blend(vec3 backColor, vec3 shapeColor, float shape)
{       
	return mix(shapeColor, backColor, smoothstep(0.0, 0.005, shape));
}

 HT for Web中《矢量手册》中自定义绘制的clock例子实现代码如下：

function init() {
	dataModel = new ht.DataModel();
	graphView = new ht.graph.GraphView(dataModel);
	view = graphView.getView();

	view.className = 'main';
	document.body.appendChild(view);
	window.addEventListener('resize', function(e) {
		graphView.invalidate();
	}, false);

	ht.Default.setCompType('clock-face', function(g, rect, comp, data, view) {
		var cx = rect.x + rect.width / 2;
		var cy = rect.y + rect.height / 2;
		var theta = 0;
		var r = Math.min(rect.width, rect.height)/2 * 0.92;
		
		g.strokeStyle = "#137";
		for (var i = 0; i < 60; i++) {                        
			g.beginPath();
			g.arc(
				cx + Math.cos(theta) * r, 
				cy + Math.sin(theta) * r, 
				i % 5 === 0 ? 4 : 1, 
				0, Math.PI * 2, true);
			g.closePath();
			g.lineWidth = i % 5 === 0 ? 2 : 1;
			g.stroke();
			theta = theta + (6 * Math.PI / 180);
		}
	});

	ht.Default.setImage('clock', {
		width: 500,
		height: 500,
		comps: [
			{
				type: 'circle',
				relative: true,
				rect: [0, 0, 1, 1],
				background: 'yellow',
				gradient: 'linear.northeast'
			},
			{
				type: 'clock-face',
				relative: true,
				rect: [0, 0, 1, 1]
			},
			{
				type: function(g, rect, comp, data, view) {
					// get current time
					var date = data.a('date');
					if(!date){
						return;
					}
					
					var hours = date.getHours();
					var minutes = date.getMinutes();
					var seconds = date.getSeconds();
					hours = hours > 12 ? hours - 12 : hours;
					var hour = hours + minutes / 60;
					var minute = minutes + seconds / 60;
					var clockRadius = 250;

					// save current context
					g.save();

					g.translate(clockRadius, clockRadius);
					g.beginPath();

					// draw numbers
					g.font = '36px Arial';
					g.fillStyle = '#000';
					g.textAlign = 'center';
					g.textBaseline = 'middle';
					for (var n = 1; n <= 12; n++) {
						var theta = (n - 3) * (Math.PI * 2) / 12;
						var x = clockRadius * 0.75 * Math.cos(theta);
						var y = clockRadius * 0.75 * Math.sin(theta);
						g.fillText(n, x, y);
					}

					// draw hour
					g.save();
					var theta = (hour - 3) * 2 * Math.PI / 12;
					g.rotate(theta);
					g.beginPath();
					g.moveTo(-15, -5);
					g.lineTo(-15, 5);
					g.lineTo(clockRadius * 0.5, 1);
					g.lineTo(clockRadius * 0.5, -1);
					g.fill();
					g.restore();

					// draw minute
					g.save();
					var theta = (minute - 15) * 2 * Math.PI / 60;
					g.rotate(theta);
					g.beginPath();
					g.moveTo(-15, -4);
					g.lineTo(-15, 4);
					g.lineTo(clockRadius * 0.8, 1);
					g.lineTo(clockRadius * 0.8, -1);
					g.fill();
					g.restore();

					// draw second
					g.save();
					var theta = (seconds - 15) * 2 * Math.PI / 60;
					g.rotate(theta);
					g.beginPath();
					g.moveTo(-15, -3);
					g.lineTo(-15, 3);
					g.lineTo(clockRadius * 0.9, 1);
					g.lineTo(clockRadius * 0.9, -1);
					g.fillStyle = '#0f0';
					g.fill();
					g.restore();

					g.restore();
				}
			}
		]
	});

	var node = new ht.Node();
	node.setPosition(150, 150);
	node.setSize(250, 250);
	node.setImage('clock');
	node.a('date', new Date());
	node.s('image.stretch', 'centerUniform');
	dataModel.add(node);

	graphView.setEditable(true);
	
	setInterval(function(){
		node.a('date', new Date());
	}, 1000);
}