矩阵分解

LU分解

 

一个可逆矩阵可以进行LU分解当且仅当它的所有子式都非零。如果要求其中的L矩阵（或U矩阵）为单位三角矩阵，那么分解是唯一的。同理可知，矩阵的LDU可分解条件也相同，并且总是唯一的。

 

即使矩阵不可逆，LU仍然可能存在。实际上，如果一个秩为k的矩阵的前k个顺序主子式不为零，那么它就可以进行LU分解，但反之则不然。

 

目前，在任意域上一个方块矩阵可进行LU分解的充要条件已经被发现，这些充要条件可以用某些特定子矩阵的秩表示。用高斯消元法来得到LU分解的算法也可以扩张到任意域上。

 

任意矩阵A（不仅仅是方块矩阵）都可以进行LUP分解。其中的L和P矩阵是方阵，U矩阵则与A形状一样。

 

对给定的N × N矩阵

 

 

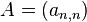
有

 

 

然后定义对于n = 1,...,N-1的情况如下：

 

在第n步，消去矩阵A^(n-1)的第n列主对角线下的元素：将A^(n-1)的第n行乘以之后加到第i行上去。其中。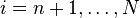

 

这相当于在A^(n-1)的左边乘上一个单位下三角矩阵：

 

 

于是，定义为：设

 

 

经过N-1轮操作后，所有在主对角线下的系数都为0了，于是我们得到了一个上三角矩阵：A^(N-1)，这时就有：

 

 

这时，矩阵A^(N-1) 就是U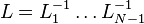，。于是我们得到分解：。

 

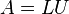显然，要是算法成立，在每步操作时必须有。如果这一条件不成立，就要将第n行和另一行交换，由此就会出现一个置换矩阵P。这就是为什么一般来说LU分解里会带有一个置换矩阵的原因。

 

奇异值分解

 

SVD分解

 

SVD 分解是LSA的数学基础，本文是我的LSA学习笔记的一部分，之所以单独拿出来，是因为SVD可以说是LSA的基础，要理解LSA必须了解SVD，因此将 LSA笔记的SVD一节单独作为一篇文章。本节讨论SVD分解相关数学问题，一个分为3个部分，第一部分讨论线性代数中的一些基础知识，第二部分讨论 SVD矩阵分解，第三部分讨论低阶近似。本节讨论的矩阵都是实数矩阵。

 

基础知识

 

1. 矩阵的秩：矩阵的秩是矩阵中线性无关的行或列的个数

 

2. 对角矩阵：对角矩阵是除对角线外所有元素都为零的方阵

 

3. 单位矩阵：如果对角矩阵中所有对角线上的元素都为零，该矩阵称为单位矩阵

 

4. 特征值：对一个M x M矩阵C和向量X，如果存在λ使得下式成立

 

 

 

则称λ为矩阵C的特征值，X称为矩阵的特征向量。非零特征值的个数小于等于矩阵的秩。

 

5. 特征值和矩阵的关系：考虑以下矩阵

 

 

该矩阵特征值λ1 = 30,λ2 = 20,λ3 = 1。对应的特征向量

 

 

假设V^T=(2,4,6) 计算S x V^T

 

 

 

有 上面计算结果可以看出，矩阵与向量相乘的结果与特征值，特征向量有关。观察三个特征值λ1 = 30,λ2 = 20,λ3 = 1，λ3值最小，对计算结果的影响也最小，如果忽略λ3，那么运算结果就相当于从(60,80,6)转变为(60,80,0)，这两个向量十分相近。这也 表示了数值小的特征值对矩阵-向量相乘的结果贡献小，影响小。这也是后面谈到的低阶近似的数学基础。

 

矩阵分解

 

1. 方阵的分解

 

1) 设S是M x M方阵，则存在以下矩阵分解

 

 

其中U 的列为S的特征向量，为对角矩阵，其中对角线上的值为S的特征值，按从大到小排列：

 

 

2) 设S是M x M 方阵，并且是对称矩阵，有M个特征向量。则存在以下分解

 

 

其中Q的列为矩阵S的单位正交特征向量，仍表示对角矩阵，其中对角线上的值为S的特征值，按从大到小排列。最后，Q^T=Q^-1，因为正交矩阵的逆等于其转置。

 

2. 奇异值分解

 

上面讨论了方阵的分解，但是在LSA中，我们是要对Term-Document矩阵进行分解，很显然这个矩阵不是方阵。这时需要奇异值分解对Term-Document进行分解。奇异值分解的推理使用到了上面所讲的方阵的分解。

 

假设C是M x N矩阵，U是M x M矩阵，其中U的列为CC^T的正交特征向量，V为N x N矩阵，其中V的列为C^TC的正交特征向量，再假设r为C矩阵的秩，则存在奇异值分解：

 

 

其中CC^T和C^TC的特征值相同，为

 

Σ为M X N，其中，其余位置数值为0，的值按大小降序排列。以下是Σ的完整数学定义：

 

 

σ_i称为矩阵C的奇异值。

 

用C乘以其转置矩阵C^T得：

 

 

上式正是在上节中讨论过的对称矩阵的分解。

 

奇异值分解的图形表示：

 

 

从图中可以看到Σ虽然为M x N矩阵，但从第N+1行到M行全为零，因此可以表示成N x N矩阵，又由于右式为矩阵相乘，因此U可以表示为M x N矩阵，V^T可以表示为N x N矩阵

 

3. 低阶近似

 

LSA潜在语义分析中，低阶近似是为了使用低维的矩阵来表示一个高维的矩阵，并使两者之差尽可能的小。本节主要讨论低阶近似和F-范数。

 

给定一个M x N矩阵C(其秩为r)和正整数k，我们希望找到一个M x N矩阵C_k，其秩不大于K。设X为C与C_k之间的差，X=C – C_k，X的F-范数为

 

 

当k远小于r时，称C_k为C的低阶近似，其中X也就是两矩阵之差的F范数要尽可能的小。

 

SVD可以被用与求低阶近似问题，步骤如下：

 

1. 给定一个矩阵C，对其奇异值分解：

 

2. 构造，它是将的第k+1行至M行设为零，也就是把的最小的r-k个(the r-k smallest)奇异值设为零。

 

3. 计算C_k：

 

回忆在基础知识一节里曾经讲过，特征值数值的大小对矩阵-向量相乘影响的大小成正比，而奇异值和特征值也是正比关系，因此这里选取数值最小的r-k个特征值设为零合乎情理，即我们所希望的C-C_k尽可能的小。完整的证明可以在Introduction to Information Retrieval^[2]中找到。

 

我们现在也清楚了LSA的基本思路：LSA希望通过降低传统向量空间的维度来去除空间中的“噪音”，而降维可以通过SVD实现，因此首先对Term-Document矩阵进行SVD分解，然后降维并构造语义空间。

 

QR分解

 

 

 

QR分解法是目前求一般矩阵全部特征值的最有效并广泛应用的方法，一般矩阵先经过正交相似变化成为 Hessenberg矩阵，然后再应用QR方法求特征值和特征向量。它是将矩阵分解成一个正规正交矩阵Q与上三角形矩阵R，所以称为QR分解法，与此正规 正交矩阵的通用符号Q有关。

 

在Matlab中，语法为[Q,R]=qr(A)，如果A是一个m×n的矩阵，其QR分解后，Q为一个m×m的矩阵，R是一个m×n的矩阵。