From Wikipedia, the free encyclopedia
The shoelace formula, or shoelace algorithm, is a mathematical
algorithm to determine the
area of a simple
polygon whose vertices are described by
ordered pairs in the plane[1]. The user cross-multiplies corresponding coordinates to find the area encompassing
the polygon, and subtracts it from the surrounding polygon to find the area of the polygon within. It is called the shoelace formula because of the constant cross-multiplying for the coordinates making up the polygon, like tying shoelaces[2].
It is also sometimes called the shoelace method. It is also known as
Gauss' area formula, after
Carl Friedrich Gauss. It has applications in surveying and forestry,[3] among other areas.
It is also called the surveyor's formula[4].
The formula can be represented by the expression:
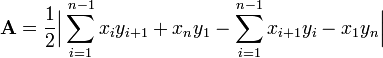

where
-
A is the area of the polygon,
-
n is the number of sides of the polygon, and
- (xi,yi), i=1,,...,n are the vertices (or "corners") of the polygon.[5]
Alternatively:[3][6]
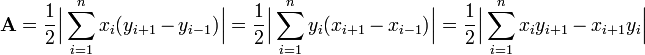
where xn+1 = x1 and x0 =
xn, as well as yn+1 =
y1 and y0 = yn.
If the points are labeled sequentially in the counterclockwise direction, then the above determinants are positive and the absolute value signs can be omitted;[4]
if they are labeled in the clockwise direction, the determinants will be negative. This is because the formula can be viewed as a special case of
Green's Theorem.
[edit]
Examples
The user must know the points of the polygon in a Cartesian plane. For example, take a triangle with coordinates {(2,1),(4,5),(7,8)}. Take the first
x-coordinate and multiply it by the second y-value, and repeat, and keep repeating this process. This can be defined by this formula:
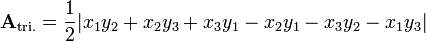
for xn and yn representing each respective coordinate. This formula is just the expansion of those given above for the case n = 3. Using it, one can find that the area of the triangle equals one half
of the
absolute value of 10+32+7−4−35−16, which equals 3. The number of variables depends on the number of sides of the
polygon. For example, a
pentagon will be defined up to
x5 and y5:

A quadrilateral will be defined up to x4 and y4:
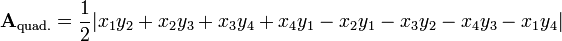
[edit]
More complex example
Consider the polygon defined by the points (3,4), (5,11), (12,8), (9,5), and (5,6), and illustrated in the following diagram:
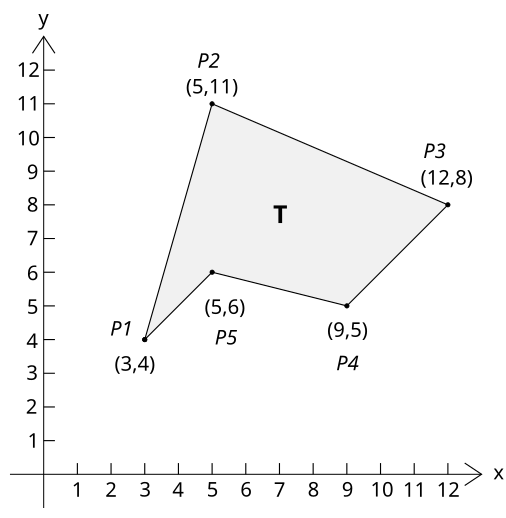
The area of this polygon is:
![\begin{align}\mathbf{A} & = {1 \over 2}|3 \times 11 + 5 \times 8 + 12 \times 5 + 9 \times 6 + 5 \times 4 \\& {} \qquad\qquad {} - 4 \times 5 - 11 \times 12 - 8 \times 9 - 5 \times 5 - 6 \times 3| \\[10pt]& = {60 \over 2} = 30\end{align}](http://upload.wikimedia.org/wikipedia/en/math/f/1/5/f15ff590fa51ea53b0d3ab7b4dfdd0aa.png)
[edit]
Explanation of name
The reason this formula is called the shoelace formula is because of a common method used to evaluate it. This method uses
matrices. As an example, choose the triangle with vertices (2,4), (3,−8), and (1,2). Then construct the following matrix by “walking around” the triangle and ending with the initial point.
 [7]
[7]
First, draw diagonal down and to the right slashes (as shown below),

and multiply the two numbers connected by each slash, then add all the products: (2×−8)+(3×2)+(1×4) = −6. Do the same with slashes diagonal down and to the left (shown below with former slashes):
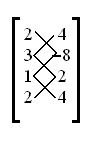
(4×3)+(−8×1)+(2×2) = 8. Then, subtract these two numbers and take the absolute value of the difference: |−6−8| = 14. Halving this gives the area of the triangle: 7. Organizing the numbers like this makes the formula easier to recall and evaluate.
With all the slashes drawn, the matrix loosely resembles a shoe with the laces done up, giving rise to the algorithm's name.
[edit]
References
分享到:







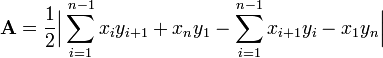

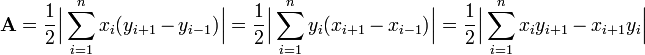
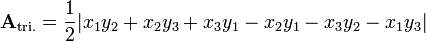

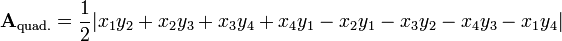

![\begin{align}\mathbf{A} & = {1 \over 2}|3 \times 11 + 5 \times 8 + 12 \times 5 + 9 \times 6 + 5 \times 4 \\& {} \qquad\qquad {} - 4 \times 5 - 11 \times 12 - 8 \times 9 - 5 \times 5 - 6 \times 3| \\[10pt]& = {60 \over 2} = 30\end{align}](http://upload.wikimedia.org/wikipedia/en/math/f/1/5/f15ff590fa51ea53b0d3ab7b4dfdd0aa.png)




相关推荐
对于简单多边形,可以采用格林公式或 shoelace formula(鞋带公式)进行计算。鞋带公式基于多边形的顶点坐标,通过连接相邻顶点形成线段,然后计算这些线段对多边形边界交叉的乘积之和。具体步骤如下: 1. 将多边形...
在计算机科学中,我们可以通过将连续的GPS点连接起来形成一个多边形,然后应用几何算法,如 shoelace formula(鞋带公式),来计算这个多边形的面积。这种方法适用于不规则形状的区域,只要确保最后一点与起始点重合...
该程序的核心在于其算法,它采用了“ shoelace formula”或称为“对角交叉法”,这是一种在二维平面上计算简单多边形面积的有效方法。算法的工作原理是通过依次记录多边形各边的顶点坐标,然后对相邻两点之间的x坐标...
可以将多边形的边界表示为一系列线段,然后用Green's theorem或者三角形法(如Shoelace formula)来计算面积。例如: ```matlab for i = 1:size(F,1) polygonVerts = V(F(i,:),:); % 获取多边形的顶点坐标 area ...
本文将深入探讨如何使用C++编程语言实现“鞋带公式”(也称为 Shoelace Formula)来解决这一问题。 “鞋带公式”是计算简单多边形(非自交)面积的一种简便方法。该公式基于向量代数,通过累加相邻顶点之间的叉积,...
计算多边形面积的方法有很多种,其中最常用的是**鞋带公式**(Shoelace Formula)。该方法通过计算多边形顶点坐标来求得面积。其基本思想是将多边形分割成一系列三角形,然后求解这些三角形的面积之和。具体来说,...
"前端项目-shoelace-css.zip" 这个标题表明这是一个与前端开发相关的项目,其中包含了名为 "shoelace-css" 的CSS工具包。"zip" 后缀则提示这是一个压缩文件,通常用于集合多个文件或目录以便于传输和存储。 **描述...
3. **鞋带公式(Shoelace Formula)**:用于计算二维平面上多边形的面积,包括地理空间中的多边形。 此外,"geo:Crystal"库可能还提供了其他功能,如: - **几何对象的操作**:例如,交集、并集和差集操作,用于...
在IT行业中,调试是软件开发过程中的重要环节,特别是在低级操作系统或引导加载程序的开发中,如Shoelace的Winiboot。Winiboot是Windows操作系统启动的一部分,负责加载内核到内存并初始化系统环境。调试此类项目...
一个基于Shoelace + LitElement的Web组件,可提供具有所选标签和下拉选项的自动完成输入。 :construction:正在施工:construction: 用法 确保已导入sl-tags-input使用的所有必要的Shoelace组件: import SlDropdown...
Shoelace Webpack示例 一个最小的设置,演示了如何通过webpack导入Shoelace组件。 为了发展: npm run start 对于生产版本: npm run build 要启动本地服务器以验证一切正常,请构建项目并运行: npx ...
shoelace.github.io
"shoelace-theme-designer-master"这个文件名可能表示这是一个项目的主分支或主版本,通常包含源代码、资源文件以及构建和部署的配置。用户可以克隆或下载这个压缩包,然后通过解压来访问项目的完整内容。在这个目录...
一个最小的设置,演示如何使用Rollup导入Shoelace组件。 为了发展: npm run start 对于生产版本: npm run build 要启动本地服务器以验证一切正常,请构建项目并运行: npx http-server 然后在显示的URL上...
计算任意多边形的面积通常采用格林公式或者 Shoelace 公式(也称为海伦-弗龙托夫公式)。格林公式是微积分中的一个结果,但在处理多边形面积时,Shoelace 公式更为直观且易于实现。下面我们将详细介绍如何使用 ...
import * as animations from '@shoelace-style/animations' ; 导入单个动画: import { bounce } from '@shoelace-style/animations' ; 进口宽松政策: import { easings } from '@shoelace-style/animations'...
本文主要介绍两种方法,即通过顶点到原点的向量叉积的一半和使用 Gauss's shoelace 公式,来计算简单多边形的面积。这两种方法在理解和实现上都相对直观,适合初学者学习。 首先,我们定义一个结构体`Point`来存储...
常用的算法有Shoelace公式(也称为对角线法则)或Green's定理。MATLAB中,我们可以利用数组和循环结构轻松地应用这些方法。 **Shoelace公式**: Shoelace公式基于多边形的顶点坐标,通过计算每一对相邻边的叉积,...