- µĄÅĶ¦ł: 285930 µ¼Ī
- µĆ¦Õł½:

- µØźĶć¬: µĄÄÕŹŚ
-

µ¢ćń½ĀÕłåń▒╗
ńżŠÕī║ńēłÕØŚ
- µłæńÜäĶĄäĶ«» ( 0)
- µłæńÜäĶ«║ÕØø ( 0)
- µłæńÜäķŚ«ńŁö ( 0)
ÕŁśµĪŻÕłåń▒╗
- 2014-06 ( 1)
- 2014-02 ( 2)
- 2013-12 ( 4)
- µø┤ÕżÜÕŁśµĪŻ...
µ£Ćµ¢░Ķ»äĶ«║
-
biglinvy’╝Ü
ķĪČķĪČķĪČ
ScrollView scrollTo ńÜäõĮ┐ńö© ÕŖ©ńö╗µĢłµ×£
ŃĆÉĶ«Īń«Śµ£║ÕøŠÕĮóÕŁ”ŃĆæÕ¤║µ£¼ÕøŠÕĮóÕģāń┤Ā’╝Üńø┤ń║┐ńÜäńö¤µłÉń«Śµ│Ģ
- ÕŹÜÕ«óÕłåń▒╗’╝Ü
- ÕēŹĶĮ”õ╣ŗķē┤(ĶĮ¼ĶĮĮ)
- androidÕŁ”õ╣Ā
08Õ╣┤9µ£łÕģźÕŁ”’╝ī12Õ╣┤7µ£łµ»ĢõĖÜ’╝īń╗ōµØ¤õ║åµłæÕ£©ĶĮ»õ╗ČÕŁ”ķÖóµäēÕ┐½õĖ░Õ»īńÜäÕż¦ÕŁ”ńö¤µ┤╗ŃĆ鵣żń│╗ÕłŚµś»Õ»╣ÕøøÕ╣┤õĖōõĖÜĶ»Šń©ŗÕŁ”õ╣ĀńÜäÕø×ķĪŠ’╝īń┤óÕ╝ĢÕÅéĶ¦ü’╝Ühttp://blog.csdn.net/xiaowei_cqu/article/details/7747205
┬Ā
ńø┤ń║┐ńÜäDDAń«Śµ│Ģ
ŃĆÉń«Śµ│Ģõ╗ŗń╗ŹŃĆæ
Ķ«Šńø┤ń║┐õ╣ŗĶĄĘńé╣õĖ║’╝łx1’╝īy1’╝ē’╝īń╗łńé╣õĖ║’╝łx2’╝īy2’╝ē’╝īÕłÖµ¢£ńÄćmõĖ║’╝Ü
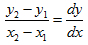
ńø┤ń║┐õĖŁńÜäµ»ÅõĖĆńé╣ÕØɵĀćķāĮÕÅ»õ╗źńö▒ÕēŹõĖĆńé╣ÕØɵĀćÕÅśÕī¢õĖĆõĖ¬Õó×ķćÅ’╝łDx, Dy’╝ēĶĆīÕŠŚÕł░’╝īÕŹ│ĶĪ©ńż║õĖ║ķĆÆÕĮÆÕ╝Å’╝Ü

Õ╣ȵ£ēÕģ│ń│╗’╝ÜDy = m ŌĆó DxŃĆéķĆÆÕĮÆÕ╝ÅńÜäÕłØÕĆ╝õĖ║ńø┤ń║┐ńÜäĶĄĘńé╣’╝łx1, y1’╝ē’╝īĶ┐ÖµĀĘ’╝īÕ░▒ÕÅ»õ╗źńö©ÕŖĀµ│ĢµØźńö¤µłÉõĖƵØĪńø┤ń║┐ŃĆéÕģĘõĮōµ¢╣µ│Ģµś»’╝Ü
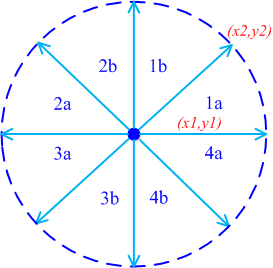
ńø┤ń║┐µ¢╣ÕÉæńÜä8õĖ¬Ķ▒ĪķÖÉ
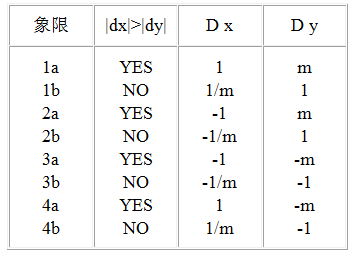
µīēńģ¦ńø┤ń║┐õ╗Ä’╝łx1’╝īy1’╝ēÕł░’╝łx2’╝īy2’╝ēńÜäµ¢╣ÕÉæõĖŹÕÉī’╝īÕłåõĖ║8õĖ¬Ķ▒ĪķÖÉŃĆéÕ»╣õ║ĵ¢╣ÕÉæÕ£©ń¼¼1aĶ▒ĪķÖÉÕåģńÜäńø┤ń║┐ĶĆīĶ©Ć’╝īD x=1’╝īD y=mŃĆéÕ»╣õ║ĵ¢╣ÕÉæÕ£©ń¼¼1bĶ▒ĪķÖÉÕåģńÜäńø┤ń║┐ĶĆīĶ©Ć’╝īÕÅ¢ÕĆ╝Dy=1’╝īDx=1/mŃĆéÕÉäĶ▒ĪķÖÉõĖŁńø┤ń║┐ńö¤µłÉµŚČDx, DyńÜäÕÅ¢ÕĆ╝ÕłŚÕ£©õĖŗĶĪ©õ╣ŗõĖŁŃĆé
┬Ā
┬Ā
- ÕĮō|dx|>|dy|µŚČ’╝ī|D x|=1, |D y|=m’╝øÕÉ”ÕłÖ’╝ÜDx=1/m’╝ī|Dy|=1
- Dx, DyńÜäń¼”ÕÅĘõĖÄdx, dyńÜäń¼”ÕÅĘńøĖÕÉī
ŃĆÉń«Śµ│ĢµĄüń©ŗÕøŠŃĆæ
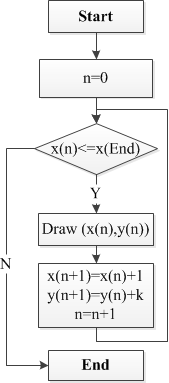
ŃĆÉńøĖÕģ│õ╗ŻńĀüŃĆæ
void PaintArea::drawLineDDA(QPainter &painter,int x0, int y0, int xEnd, int yEnd)
{
int dx=xEnd-x0,dy=yEnd-y0,steps,k;
float xIncrement,yIncrement,x=x0,y=y0;
if(fabs(dx)>fabs(dy)) steps=fabs(dx);
else steps=fabs(dy);
xIncrement=float(dx)/float(steps);
yIncrement=float(dy)/float(steps);
painter.drawPoint(round(x),round(y));
for(k=0;k<steps;k++){
x+=xIncrement;
y+=yIncrement;
painter.drawPoint(round(x),round(y));
}
}
ńø┤ń║┐ńÜäBresenhamń«Śµ│Ģ
Ķ┐ÖõĖ¬ń«Śµ│Ģńö▒BresenhamÕ£©1965Õ╣┤µÅÉÕć║ŃĆéĶ«Šńø┤ń║┐õ╗ÄĶĄĘńé╣’╝łx1, y1’╝ēÕł░ń╗łńé╣’╝łx2, y2’╝ēŃĆéńø┤ń║┐ÕÅ»ĶĪ©ńż║õĖ║µ¢╣ń©ŗy=mx+bŃĆéÕģČõĖŁ
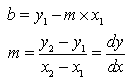
µłæõ╗¼ńÜäĶ«©Ķ«║ÕģłÕ░åńø┤ń║┐µ¢╣ÕÉæķÖÉõ║Ä1aĶ▒ĪķÖÉÕ£©Ķ┐Öń¦ŹµāģÕåĄõĖŗ’╝īÕĮōńø┤ń║┐ÕģēµĀģÕī¢µŚČ’╝īxµ»Åµ¼ĪķāĮÕó×ÕŖĀ1õĖ¬ÕŹĢÕģā’╝īÕŹ│
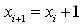
ĶĆīyńÜäńøĖÕ║öÕó×ÕŖĀÕ║öÕĮōÕ░Åõ║Ä1ŃĆéõĖ║õ║åÕģēµĀģÕī¢’╝īyi+1ÕŬÕÅ»ĶāĮķĆēµŗ®Õ”éõĖŗõĖżń¦ŹõĮŹńĮ«õ╣ŗõĖĆ’╝łÕ”éÕøŠ’╝ēŃĆé
i+1ńÜäõĮŹńĮ«ķĆēµŗ®yi-1=yi µł¢ĶĆģ yi+1=yi+1
ķĆēµŗ®ńÜäÕÄ¤ÕłÖµś»ń£ŗń▓ŠńĪ«ÕĆ╝yõĖÄyiÕÅŖyi+1ńÜäĶĘØń”╗d1ÕÅŖd2ńÜäÕż¦Õ░ÅĶĆīÕ«ÜŃĆéĶ«Īń«ŚÕ╝ÅõĖ║’╝Ü
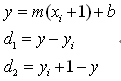
Õ”éµ×£d1-d2>0’╝īÕłÖyi+1=yi+1’╝īÕÉ”ÕłÖyi+1=yiŃĆéÕøĀµŁżń«Śµ│ĢńÜäÕģ│ķö«Õ£©õ║Äń«ĆõŠ┐Õ£░µ▒éÕć║d1-d2ńÜäń¼”ÕÅĘŃĆéÕ░åõĖŖÕģ¼Õ╝ÅÕŠŚ
d1-d2=2y-2yi-1=2 (xi+1)-2yi+2b-1
ńö©dxõ╣śńŁēÕ╝ÅõĖżĶŠ╣’╝īÕ╣Čõ╗źPi=dx(d1-d2)õ╗ŻÕģźõĖŖĶ┐░ńŁēÕ╝Å’╝īÕŠŚ
Pi=2xidy-2yidx+2dy+dx(2b-1)
d1-d2µś»µłæõ╗¼ńö©õ╗źÕłżµ¢Łń¼”ÕÅĘńÜäĶ»»ÕĘ«ŃĆéńö▒õ║ÄÕ£©1aĶ▒ĪķÖÉ’╝īdxµĆ╗Õż¦õ║Ä0’╝īµēĆõ╗źPiõ╗ŹµŚ¦ÕÅ»õ╗źńö©õĮ£Õłżµ¢Łń¼”ÕÅĘńÜäĶ»»ÕĘ«ŃĆéPi-1õĖ║’╝Ü
Pi+1=Pi+2dy-2dx(yi+1-yi)
Ķ»»ÕĘ«ńÜäÕłØÕĆ╝P1’╝īÕÅ»Õ░åx1, y1’╝īÕÆībõ╗ŻÕģźÕ╝Å’╝ł4’╝ēõĖŁńÜäxi, yiĶĆīÕŠŚÕł░’╝Ü
P1=2dy-dx
┬Ā
Bresenhamń«Śµ│ĢńÜäõ╝śńé╣µś»’╝Ü
-
õĖŹńö©µĄ«ńé╣µĢ░’╝īÕŬńö©µĢ┤µĢ░’╝ø
-
ÕŬÕüܵĢ┤µĢ░ÕŖĀÕćŵ│ĢÕÆīõ╣ś2Ķ┐Éń«Ś’╝īĶĆīõ╣ś2Ķ┐Éń«ŚÕÅ»õ╗źńö©ńĪ¼õ╗Čń¦╗õĮŹÕ«×ńÄ░ŃĆé
-
Bresenhamń«Śµ│ĢķƤÕ║”ÕŠłÕ┐½’╝īÕ╣ČķĆéõ║Äńö©ńĪ¼õ╗ČÕ«×ńÄ░ŃĆé
┬Ā
ŃĆÉń«Śµ│ĢµĄüń©ŗÕøŠŃĆæ
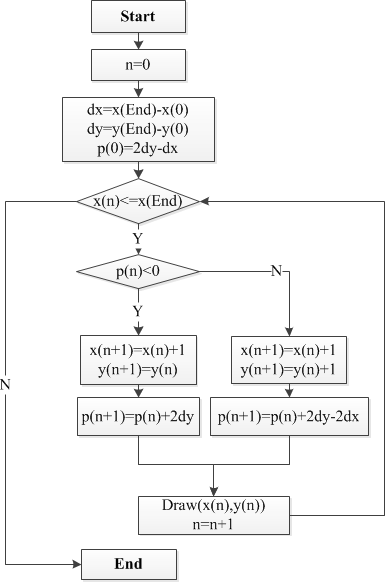
┬Ā
ŃĆÉńøĖÕģ│õ╗ŻńĀüŃĆæ
void PaintArea::drawLineBresenham(QPainter &painter, int x0, int y0, int xEnd, int yEnd)
{
int x,y,dx,dy,e;
if(fabs(x0-xEnd)>fabs(y0-yEnd)){
dx=xEnd-x0; dy=yEnd-y0; e=-dx;
x=x0; y=y0;
for(int i=0;i<=dx;i++)
{painter.drawPoint(x,y);
x=x+1; e=e+2*dy;
if(e>=0) {y=y+1; e=e-2*dx; }}
}
else if(fabs(x0-xEnd)>fabs(y0-yEnd)){
dx=xEnd-x0; dy=yEnd-y0; e=-dx;
x=x0; y=y0;
for(int i=0;i<=dx;i++)
{ painter.drawPoint(x,y);
y=y+1; e=e+2*dx;
if(e>=0) {x=x+1; e=e-2*dy; }}
}
}
┬Ā
õĖŁńé╣ńö╗ń║┐µ│Ģ
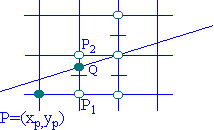
ÕüćÕ«Üńø┤ń║┐µ¢£ńÄćkÕ£©0~1õ╣ŗķŚ┤’╝īÕĮōÕēŹĶ▒Īń┤Āńé╣õĖ║’╝łxp,yp’╝ē’╝īÕłÖõĖŗõĖĆõĖ¬Ķ▒Īń┤Āńé╣µ£ēõĖżń¦ŹÕÅ»ķĆēµŗ®ńé╣’╝łxp+1,yp’╝ēµł¢P2’╝łxp+1,yp+1’╝ēŃĆéĶŗźP1õĖÄP2ńÜäõĖŁńé╣’╝łxp+1,yp+0.5’╝ēń¦░õĖ║M’╝īQõĖ║ńÉåµā│ńø┤ń║┐õĖÄx=xp+1Õ×éń║┐ńÜäõ║żńé╣ŃĆéÕĮōMÕ£©QńÜäõĖŗµ¢╣µŚČ’╝īÕłÖÕÅ¢P2Õ║öõĖ║õĖŗõĖĆõĖ¬Ķ▒Īń┤Āńé╣’╝øÕĮōMÕ£©QńÜäõĖŖµ¢╣µŚČ’╝īÕłÖÕÅ¢P1õĖ║õĖŗõĖĆõĖ¬Ķ▒Īń┤Āńé╣ŃĆéĶ┐ÖÕ░▒µś»õĖŁńé╣ńö╗ń║┐µ│ĢńÜäÕ¤║µ£¼ÕĤńÉåŃĆé
┬Ā
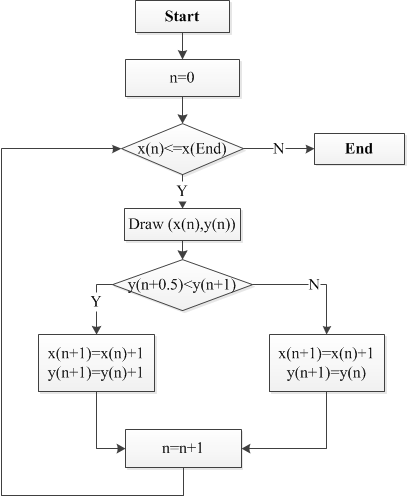
ŃĆÉń«Śµ│ĢµĄüń©ŗÕøŠŃĆæ
┬Ā
┬Ā
ŃĆÉńøĖÕģ│õ╗ŻńĀüŃĆæ
void PaintArea::drawLineMiddle(QPainter &painter, int x0, int y0, int xEnd, int yEnd)
{
int a,b,d,x,y;
if(fabs(x0-xEnd)>fabs(y0-yEnd)){
a=y0-yEnd; b=xEnd-x0; d=2*a+b; x=x0; y=y0;
painter.drawPoint(x,y);
while(x<xEnd)
{ if(d<0) {x++;y++;d+=2*(a+b); }
else{x++;d+=2*a; }
painter.drawPoint(x,y);
}
}
else if(fabs(x0-xEnd)>fabs(y0-yEnd) &&(x0-xEnd))<0)){
a=y0-yEnd; b=xEnd-x0; d=2*a+b; x=x0; y=y0;
painter.drawPoint(x,y);
while(x>xEnd)
{ if(d<0) {x--;y--; d-=2*(a+b); }
else{x--;d-=2*a; }
painter.drawPoint(x,y);
}
}
else if(fabs(x0-xEnd)<fabs(y0-yEnd)&&(x0-xEnd)<0){
a=y0-yEnd; b=xEnd-x0; d=2*a+b; x=x0; y=y0;
painter.drawPoint(x,y);
while(y>yEnd)
{ if(d<0) {y++;x++;d+=2*(a+b); }
else{y++;d+=2*a; }
painter.drawPoint(x,y);
}
}
else if(fabs(x0-xEnd)<fabs(y0-yEnd) &&(x0-xEnd))>0)){
a=y0-yEnd; b=xEnd-x0; d=2*a+b; x=x0; y=y0;
painter.drawPoint(x,y);
while(x>xEnd)
{ if(d<0) {x--;y--; d-=2*(a+b); }
else{x--;d-=2*a; }
painter.drawPoint(x,y);
}
}
else if(fabs(x0-xEnd)<fabs(y0-yEnd)&&(x0-xEnd)>0){
a=y0-yEnd; b=xEnd-x0; d=2*a+b; x=x0; y=y0;
painter.drawPoint(x,y);
while(y>yEnd)
{ if(d<0) {y++;x++;d+=2*(a+b); }
else{y++;d+=2*a; }
painter.drawPoint(x,y);
}
}
}
┬Ā
ĶĮ»õ╗ȵł¬ÕøŠ

┬Ā
Ķ┐ÖõĖ¬ń╗śÕøŠĶĮ»õ╗ȵś»ńö©QTÕåÖńÜä’╝īµłæõ╝ÜÕÅ”Õż¢ÕåÖõĖĆń»ćõ╗ŗń╗Źń╝¢ń©ŗń╗ōµ×ä’╝īµĢ¼Ķ»Ęµ£¤ÕŠģ~
┬Ā
ń╗ōµ×£Õłåµ×É
-
µŁżµ¼ĪÕ«×ķ¬īĶć¬ÕĘ▒ń£¤ńÜäÕĆŠµ│©õ║åÕŠłÕż¦ńÜäÕ┐āĶĪĆŃĆé
ÕøĀõĖ║ÕŠłÕ¢£µ¼óĶ«Īń«Śµ£║ÕøŠÕĮóÕŁ”’╝īµēĆõ╗źÕŠłµā│ÕüÜõĖ¬Õāŵ©ĪÕāŵĀĘńÜäõĖ£Ķź┐Õć║µØź’╝īõ║ĵś»Õ░▒õĖŗÕ«ÜÕå│Õ┐āÕĆ¤Õ«×ķ¬īńÜäµ£║õ╝ÜÕüÜõĖ¬ń«ĆµśōńÜäwindowsńö╗µØ┐ŃĆéõ╣¤µś»ń¼¼õĖƵ¼ĪµŁŻÕ╝ÅńÜäõĮ┐ńö©QTÕ╝ĆÕÅæ’╝īµæĖń┤óńÜäĶ┐ćń©ŗõĮ┐ÕŠŚµĢ┤õĖ¬Õ«×ķ¬īµŗ¢õ║åÕŠłķĢ┐µŚČķŚ┤ŃĆéµ£Ćń╗łńÜäń╗ōµ×£Ķ┐śµś»µ»öĶŠāõ╗żĶć¬ÕĘ▒µ╗ĪµäÅńÜä’╝īĶć│Õ░æÕ¤║µ£¼ÕŖ¤ĶāĮķāĮÕ«×ńÄ░õ║å’╝īńĢīķØóõ╣¤Ķ┐śń£ŗÕŠŚĶ┐ćÕÄ╗ŃĆé -
Ķ┐ćõ║ĵ│©ķćŹĶĪ©ķØó’╝īń«Śµ│ĢõĖŖÕŖ¤Õż½õĖŹĶČ│’╝īµ£ēõ║øŌĆ£ĶłŹµ£¼ķĆɵ£½ŌĆØ
µłæµś»µŖŖµĢ┤õĖ¬ĶĮ»õ╗ČÕüÜÕĘ«õĖŹÕżÜõ║å’╝īµēŹÕ╝ĆÕ¦ŗń╗åń╗åÕŠŚµØźńĀöń®ČÕøŠÕģāńÜäÕ¤║µ£¼ń«Śµ│Ģ’╝łÕ╝ĆÕ¦ŗķāĮµś»Ķ░āńö©qtĶć¬ÕĖ”ńÜäń╗śÕłČÕćĮµĢ░’╝ēŃĆéĶ░āĶ»Ģń«Śµ│ĢńÜäĶ┐ćń©ŗµēŹµĘ▒Õł╗µä¤Ķ¦ēĶ┐Öµ»öµĢ┤õĖ¬ĶĮ»õ╗ȵø┤ĶŖ▒µŚČķŚ┤’╝łÕÅ»ĶāĮÕøĀõĖ║µĢ┤õĖ¬ĶĮ»õ╗ČÕ╣ȵ▓Īµ£ēÕŠłÕżŹµØéńÜäµ×ȵ×ä’╝ēŃĆéńö▒õ║ĵŚČķŚ┤µ£ēķÖÉ’╝īÕŠłÕżÜÕ£░µ¢╣µ▓Īµ£ēń╗åń╗åµö╣Ķ┐øŃĆéÕ░żÕģȵś»Õ»╣õ║ÄkńÜäÕćĀń¦ŹµāģÕåĄ’╝īÕ░▒ńö¤ńö¤ńÜäÕåÖõ║åÕŠłÕåŚõĮÖńÜäõ╗ŻńĀü’╝īÕ«×Õ£©µś»õĖæÕĢŖŃĆé -
õ╗źÕÉÄÕåŹń╗¦ń╗Łµö╣Ķ┐øŃĆé
Ķ”üµö╣Ķ┐øńÜäÕ£░µ¢╣Ķ┐śµ£ēÕŠłÕżÜŃĆéµ»öÕ”éń«Śµ│Ģń╗ōµ×äķ揵×ä’╝īõĖŹĶ”üÕåÖķéŻõ╣łÕåŚõĮÖŃĆéńäČÕÉÄÕåŹÕ░ØĶ»ĢõĖĆõ║øÕĪ½Õģģń«Śµ│ĢĶć¬ÕĘ▒Õ«×ńÄ░’╝īĶ┐śµ£ēĶć¬ÕĘ▒õ╝ÜĶ»ĢńØĆÕüÜÕüÜń«ĆÕŹĢńÜäÕøŠÕāÅÕżäńÉå’╝īÕÅśÕĮóµŗēõ╝Ėõ╗Ćõ╣łńÜäŃĆé
µĆ╗õ╣ŗ’╝īÕØܵīüÕŖ©µēŗ’╝īÕŁ”õ╗źĶć┤ńö©ŃĆé
ĶĮ¼ĶĮĮĶ»Ęµ│©µśÄÕć║Õżä’╝Ühttp://blog.csdn.net/xiaowei_cqu/article/details/7762419
- 2012-08-23 14:02
- µĄÅĶ¦ł 1078
- Ķ»äĶ«║(0)
- Õłåń▒╗:ń¦╗ÕŖ©Õ╝ĆÕÅæ
- µ¤źń£ŗµø┤ÕżÜ
ÕÅæĶĪ©Ķ»äĶ«║
-
unityÕ¤║ńĪĆÕ╝ĆÕÅæ----ńē®õĮōõĮŹń¦╗ÕÆīµŚŗĶĮ¼Õ«×ńö©õ╗ŻńĀü
2013-11-21 22:46 1277using UnityEngine; using Syst ... -
android ÕŖ©µĆüµŚČķƤ ķÖäµ║ÉńĀü
2013-09-24 12:03 1344┬Ā ┬Ā Ķć¬Õ«Üõ╣ēViewÕ«×ĶĘĄ õŠŗÕŁÉõ╗ŻńĀü Ķć¬Õ«Üõ╣ēÕŖ©µĆüµŚČķƤ ... -
android Dialog ĶāīµÖ»ķŚ«ķóś
2013-08-14 11:22 1214┬Ā ┬Ā ┬Ā ┬Āµłæõ╗¼Õ£©õĮ┐ńö©Ķć¬Õ«Üõ╣ēńÜäDialogńÜ䵌ČÕĆÖ’╝īÕ¢£µ¼óĶć¬ÕĘ▒ ... -
ScrollView scrollTo ńÜäõĮ┐ńö© ÕŖ©ńö╗µĢłµ×£
2013-08-05 17:43 4633┬Ā ┬Āõ╗ŖÕż®ńö©Õł░õ║åScrollView scrollToµ¢╣µ│Ģ ... -
AndroidõĖŁViewń╗śÕłČõ╝śÕī¢õ╣ŗõĖĆ---- õ╝śÕī¢ÕĖāÕ▒ĆÕ▒éµ¼Ī
2012-09-04 23:00 1094┬Ā ┬Ā ┬Ā ... -
AndroidõĖŁViewń╗śÕłČõ╝śÕī¢õ║īõĖĆ---- õĮ┐ńö©<include />µĀćńŁŠÕżŹńö©ÕĖāÕ▒Ƶ¢ćõ╗Č
2012-09-08 13:54 1072┬Ā ... -
AndroidõĖŁViewń╗śÕłČõ╝śÕī¢õ╣ŗõĖē---- õ╝śÕī¢View
2012-09-13 21:00 1095┬Ā ... -
Õģ░µ×Śõ╗╗ÕŖĪń«ĪńÉåÕ║öńö©ń©ŗÕ║ÅķøÅÕĮóńēłõ╗źÕÅŖµ”éĶ”üĶ»┤µśÄ
2012-09-15 21:54 890... -
AndroidõĖŁmeasureĶ┐ćń©ŗŃĆüWRAP_CONTENTĶ»”Ķ¦Żõ╗źÕÅŖxmlÕĖāÕ▒Ƶ¢ćõ╗ČĶ¦Żµ×ɵĄüń©ŗµĄģµ×É(õĖŖ)
2012-10-10 18:14 1187... -
AndroidõĖŁmeasureĶ┐ćń©ŗŃĆüWRAP_CONTENTĶ»”Ķ¦Żõ╗źÕÅŖxmlÕĖāÕ▒Ƶ¢ćõ╗ČĶ¦Żµ×ɵĄüń©ŗµĄģµ×É(õĖŗ)
2012-10-17 20:05 885... -
AndroidõĖŁµ¢ćõ╗ČķĆēµŗ®ÕÖ©ńÜäÕ«×ńÄ░
2012-11-30 08:59 1198... -
ŃĆÉń╝¢Ķ»æÕĤńÉåŃĆæõĮ┐ńö©LexÕ░åC/C++µ¢ćõ╗ČĶŠōÕć║õĖ║HTMLµ¢ćõ╗Č
2012-07-20 09:37 109308Õ╣┤9µ£łÕģźÕŁ”’╝ī12Õ╣┤7µ£łµ»ĢõĖÜ’╝īń╗ōµØ¤õ║åµłæÕ£©ĶĮ»õ╗ČÕŁ”ķÖóµäēÕ┐½õĖ░Õ»īńÜäÕż¦ ... -
ŃĆÉń╝¢Ķ»æÕĤńÉåŃĆæµŁŻÕłÖĶĪ©ĶŠŠÕ╝Å
2012-07-21 21:49 234008Õ╣┤9µ£łÕģźÕŁ”’╝ī12Õ╣┤7µ£łµ»ĢõĖÜ’╝īń╗ōµØ¤õ║åµłæÕ£©ĶĮ»õ╗ČÕŁ”ķÖóµäēÕ┐½õĖ░Õ»īńÜäÕż¦ ... -
ŃĆÉOpenCVŃĆæĶ«┐ķŚ«MatÕøŠÕāÅõĖŁµ»ÅõĖ¬ÕāÅń┤ĀńÜäÕĆ╝
2012-07-22 07:10 1193õ╗ŖÕż®ńÖŠÕ║”µÉ£ĶĄäµ¢ÖĶ┐śµÉ£Õł░õ║åĶć¬ÕĘ▒ńÜäŃĆéŃĆéŃĆéŃĆŖĶ«┐ķŚ«ÕøŠÕāÅõĖŁµ»ÅõĖ¬ÕāÅń┤ĀńÜäÕĆ╝ ... -
ŃĆÉń╝¢Ķ»æÕĤńÉåŃĆæńö©YaccÕüÜĶ»Łµ│ĢÕłåµ×É
2012-07-23 05:47 181808Õ╣┤9µ£łÕģźÕŁ”’╝ī12Õ╣┤7µ£łµ»Ģõ ... -
ŃĆÉUMLŃĆæUMLÕćĀń¦ŹÕøŠńÜäń╗śÕłČ
2012-07-24 09:49 100108Õ╣┤9µ£łÕģźÕŁ”’╝ī12Õ╣┤7µ£łµ»ĢõĖÜ’╝īń╗ōµØ¤õ║åµłæÕ£©ĶĮ»õ╗ČÕŁ”ķÖóµäēÕ┐½õĖ░Õ»īńÜäÕż¦ ... -
ŃĆÉOpenCVŃĆæķé╗Õ¤¤µ╗żµ│ó’╝ܵ¢╣µĪåŃĆüķ½śµ¢»ŃĆüõĖŁÕĆ╝ŃĆüÕÅīĶŠ╣µ╗żµ│ó
2012-07-26 10:52 1475ķé╗Õ¤¤µ╗żµ│ó’╝łÕŹĘń¦»’╝ē ķé╗Õ¤¤ń«ŚÕŁÉÕĆ╝Õł®ńö©ń╗ÖÕ«ÜÕāÅń┤Ā ... -
ŃĆɵĢ░µŹ«ń╗ōµ×äŃĆæµÄÆÕ║Åń«Śµ│Ģ’╝ÜÕĖīÕ░öŃĆüÕĮÆÕ╣ČŃĆüÕ┐½ķƤŃĆüÕĀåµÄÆÕ║Å
2012-07-28 06:15 103808Õ╣┤9µ£łÕģźÕŁ”’╝ī12Õ╣┤7µ£łµ»Ģõ ... -
ŃĆÉOpenCVŃĆæĶ¦Æńé╣µŻĆµĄŗ’╝ÜHarrisĶ¦Æńé╣ÕÅŖShi-TomasiĶ¦Æńé╣µŻĆµĄŗ
2012-07-31 13:25 1556Ķ¦Æńé╣ ńē╣ÕŠüµŻĆµĄŗõĖÄÕī╣ķģŹµś ... -
ŃĆÉUMLŃĆæµĪłõŠŗÕłåµ×É’╝ܵ£║Õ£║Ķ┐ÉõĮ£ń│╗ń╗¤
2012-08-01 17:22 315908Õ╣┤9µ£łÕģźÕŁ”’╝ī12Õ╣┤7µ£łµ»Ģõ ...





ńøĖÕģ│µÄ©ĶŹÉ
5. ńø┤ń║┐ńö¤µłÉń«Śµ│Ģ’╝Üńø┤ń║┐ńö¤µłÉń«Śµ│Ģµś»Ķ«Īń«Śµ£║ÕøŠÕĮóÕŁ”õĖŁńÜäÕ¤║µ£¼ń«Śµ│Ģ’╝īÕīģµŗ¼µĢ░ÕĆ╝ÕŠ«Õłåµ│Ģ’╝łDDA’╝ēŃĆüõĖŁńé╣ńö╗ń║┐ń«Śµ│ĢÕÆīBresenhamńö╗ń║┐ń«Śµ│ĢŃĆéĶ┐Öõ║øń«Śµ│ĢÕÅ»õ╗źńö¤µłÉńø┤ń║┐ŃĆüÕ£åÕÆīÕģČõ╗¢ÕøŠÕĮóŃĆé 6. õĖŁńé╣ńö╗ń║┐ń«Śµ│Ģ’╝ÜõĖŁńé╣ńö╗ń║┐ń«Śµ│Ģµś»ńø┤ń║┐ńö¤µłÉń«Śµ│ĢńÜäõĖĆń¦Ź...
Ķ«Īń«Śµ£║ÕøŠÕĮóÕŁ” ńø┤ń║┐DDAń«Śµ│ĢĶ«Īń«Śµ£║ÕøŠÕĮóÕŁ” ńø┤ń║┐DDAń«Śµ│ĢĶ«Īń«Śµ£║ÕøŠÕĮóÕŁ” ńø┤ń║┐DDAń«Śµ│ĢĶ«Īń«Śµ£║ÕøŠÕĮóÕŁ” ńø┤ń║┐DDAń«Śµ│ĢĶ«Īń«Śµ£║ÕøŠÕĮóÕŁ” ńø┤ń║┐DDAń«Śµ│ĢĶ«Īń«Śµ£║ÕøŠÕĮóÕŁ” ńø┤ń║┐DDAń«Śµ│ĢĶ«Īń«Śµ£║ÕøŠÕĮóÕŁ” ńø┤ń║┐DDAń«Śµ│ĢĶ«Īń«Śµ£║ÕøŠÕĮóÕŁ” ńø┤ń║┐DDAń«Śµ│ĢĶ«Īń«Śµ£║...
Õ«×ķ¬īńÜäõĖ╗Ķ”üńø«µĀ浜»µÄīµÅĪ3ń¦ŹÕĖĖĶ¦üńÜäńø┤ń║┐ńö¤µłÉń«Śµ│Ģ’╝ܵĢ░ÕĆ╝ÕŠ«Õłå’╝łDDA’╝ēń«Śµ│ĢŃĆüõĖŁńé╣ń«Śµ│Ģõ╗źÕÅŖBresenhamń«Śµ│Ģ’╝īÕ╣ČĶāĮÕż¤Õ£©MFCńÄ»ÕóāõĖŗµŁŻńĪ«ń╗śÕłČńø┤ń║┐ŃĆé **1. DDA’╝łDigital Differential Analyzer’╝ēń«Śµ│Ģ** DDAń«Śµ│ĢÕ¤║õ║Äńø┤ń║┐µ¢╣ń©ŗy = kx +...
3. **ńø┤ń║┐ńö¤µłÉń«Śµ│Ģ**’╝ÜBresenhamń«Śµ│Ģµś»µ£ĆÕĖĖĶ¦üńÜäńø┤ń║┐ńö¤µłÉń«Śµ│Ģ’╝īÕ«āĶāĮÕ£©ń”╗µĢŻńÜäÕāÅń┤ĀńĮæµĀ╝õĖŖĶ┐æõ╝╝Õ£░ń╗śÕłČÕć║ńø┤ń║┐ŃĆéÕ«×ķ¬īÕÅ»ĶāĮõ╝ÜĶ”üµ▒éõĮĀÕ«×ńÄ░Ķ┐ÖõĖ¬ń«Śµ│Ģ’╝īõ╗źÕ£©Õ▒ÅÕ╣ĢõĖŖń▓ŠńĪ«Õ£░ńö╗Õć║ńø┤ń║┐ŃĆé 4. **µżŁÕ£åÕÆīÕ£åńÜäńö¤µłÉ**’╝ÜĶÖĮńäČńø┤ń║┐ÕÅ»õ╗źķĆÜĶ┐ć...
Bresenhamń«Śµ│Ģµś»Ķ«Īń«Śµ£║ÕøŠÕĮóÕŁ”õĖŁµ£ĆĶæŚÕÉŹńÜäńø┤ń║┐ńö¤µłÉń«Śµ│Ģ’╝īńö▒Jack Bresenhamõ║Ä1965Õ╣┤µÅÉÕć║ŃĆéÕ«āÕ¤║õ║ÄĶ»»ÕĘ«ń┤»ń¦»ńÜäµĆصā│’╝īõ╗źµĢ┤µĢ░ÕØɵĀćõĖ║õĖŁÕ┐ā’╝īķĆÜĶ┐ćµ»öĶŠāĶ»»ÕĘ«ÕĆ╝ńÜäÕż¦Õ░ÅµØźÕå│Õ«ÜõĖŗõĖƵŁźÕÉæÕō¬õĖ¬µ¢╣ÕÉæń¦╗ÕŖ©ŃĆéÕ»╣õ║ÄyĶĮ┤µŁŻµ¢╣ÕÉæńÜäńø┤ń║┐’╝īń«Śµ│ĢÕÅ»õ╗ź...
Õ¤║µ£¼õ║īń╗┤ÕøŠÕģāńÜäńö¤µłÉń«Śµ│Ģµś»Ķ«Īń«Śµ£║ÕøŠÕĮóÕŁ”õĖŁµ£ĆÕ¤║ńĪĆńÜäķā©Õłå’╝īÕ«āõ╗¼µś»µ×䵳ÉÕøŠÕĮóÕøŠÕāÅńÜäÕ¤║µ£¼Õģāń┤ĀŃĆéĶ┐Öõ║øÕøŠÕģāńÜäńö¤µłÉń«Śµ│ĢÕÅ»õ╗źÕłåõĖ║õĖżµŁź’╝Üķ”¢Õģł’╝īńĪ«Õ«ÜÕøŠÕĮóÕ»╣Õ║öńÜäĶ▒Īń┤ĀķøåÕÉłÕÅŖÕģČķó£Ķē▓’╝øÕģȵ¼Ī’╝īńö©ÕøŠÕĮóńÜäķó£Ķē▓µł¢ÕģČõ╗¢Õ▒×µĆ¦Õ»╣Ķ▒Īń┤ĀĶ┐øĶĪīÕåÖµōŹõĮ£ŃĆé...
2. µÄīµÅĪÕćĀń¦ŹÕ¤║µ£¼ńÜäńø┤ń║┐ńö¤µłÉń«Śµ│Ģ’╝ÜDDA ń«Śµ│ĢŃĆüBresenham ńö╗ń║┐µ│ĢŃĆüõĖŁńé╣ńö╗ń║┐µ│Ģ 3. Õ«×ńÄ░ńø┤ń║┐ńö¤µłÉńÜä’╝īÕ£©Õ▒ÅÕ╣ĢõĖŖõ╗╗µäÅńö¤µłÉõĖƵØĪńø┤ń║┐ õĖēŃĆüÕ«×ńÄ░ń©ŗÕ║Å’╝Ü µ£¼Õ«×ķ¬īõĮ┐ńö© C Ķ»ŁĶ©Ćń╝¢ÕåÖ’╝īõĮ┐ńö© Borland Graphics Interface’╝łBGI’╝ēÕ║ōµØźÕ«×ńÄ░...
Õ£©Ķ«Īń«Śµ£║ÕøŠÕĮóÕŁ”õĖŁ’╝īńø┤ń║┐ńö¤µłÉń«Śµ│Ģµś»Õ¤║ńĪĆõĖöĶć│Õģ│ķćŹĶ”üńÜä’╝īÕ«āõĮ┐ÕŠŚĶ«Īń«Śµ£║ĶāĮÕż¤ń▓ŠńĪ«Õ£░µÅÅń╗śÕć║ńø┤ń║┐’╝īõĖ║ÕżŹµØéńÜäÕøŠÕĮóµĖ▓µ¤ōÕÆīÕøŠÕāÅÕżäńÉåµÅÉõŠøÕ¤║ńĪĆŃĆéÕ£©Windowsń╝¢ń©ŗńÄ»ÕóāõĖŁ’╝īVC++’╝łVisual C++’╝ēÕĖĖĶó½ńö©õ║ÄÕ╝ĆÕÅæÕøŠÕĮóÕ║öńö©’╝īÕøĀµŁżńÉåĶ¦ŻÕ╣ȵÄīµÅĪńø┤ń║┐...
ńø┤ń║┐õĮ£õĖ║µ£ĆÕ¤║ńĪĆńÜäÕøŠÕĮóÕģāń┤Āõ╣ŗõĖĆ’╝īÕ£©Ķ«Īń«Śµ£║ÕøŠÕĮóÕŁ”õĖŁµē«µ╝öńØĆĶć│Õģ│ķćŹĶ”üńÜäĶ¦ÆĶē▓ŃĆéµ£¼ķĪ╣ńø«ķćŹńé╣õ╗ŗń╗Źõ║åõĖēń¦Źń╗ÅÕģĖńÜäńø┤ń║┐ń╗śÕłČń«Śµ│Ģ’╝ÜDDA’╝łDigital Differential Analyzer’╝īµĢ░ÕŁŚÕŠ«ÕłåÕłåµ×ÉÕÖ©’╝ēŃĆüBresenhamń«Śµ│Ģõ╗źÕÅŖõĖŁńé╣ńö╗ń║┐µ│Ģ’╝īĶ┐Öõ║øķāĮµś»...
ÕøŠÕģāõĮ£õĖ║Ķ«Īń«Śµ£║ÕøŠÕĮóÕŁ”õĖŁńÜäÕ¤║µ£¼Õģāń┤Ā’╝īµś»µ×äÕ╗║ÕżŹµØéÕøŠÕĮóńÜäÕ¤║ńĪĆŃĆéÕ«āõ╗¼µś»õĖŹÕÅ»ÕåŹÕłåńÜäÕ¤║µ£¼ÕøŠÕĮóÕ«×õĮō’╝īõŠŗÕ”éńé╣ŃĆüńø┤ń║┐ŃĆüÕ£åÕ╝¦ŃĆüÕżÜĶŠ╣ÕĮóŃĆüÕŁŚõĮōń¼”ÕÅĘõ╗źÕÅŖõĮŹÕøŠńŁēŃĆéÕ£©Õ«×ķÖģÕ║öńö©õĖŁ’╝īÕżŹµØéńÜäÕøŠÕĮóÕÅ»õ╗źķĆÜĶ┐ćĶ┐Öõ║øÕ¤║µ£¼ÕøŠÕģāńÜäõĖŹÕÉīń╗äÕÉłµØźÕ«×ńÄ░ŃĆé **...
Õ£©Ķ«Īń«Śµ£║ÕøŠÕĮóÕŁ”õĖŁ’╝īńø┤ń║┐ÕÆīÕ£åµś»µ£ĆÕ¤║µ£¼ńÜäÕøŠÕĮóÕģāń┤Ā’╝īµ£¼µ¢ćÕ░åõ╗ŗń╗ŹõĖēń¦Źńø┤ń║┐ńö¤µłÉń«Śµ│ĢÕÆīÕ£åńÜäńö¤µłÉń«Śµ│ĢŃĆé õĖĆŃĆüDDA ńø┤ń║┐ńö¤µłÉń«Śµ│Ģ DDA ńø┤ń║┐ńö¤µłÉń«Śµ│Ģµś»õĖĆń¦Źń«ĆÕŹĢńÜäńø┤ń║┐ńö¤µłÉń«Śµ│ĢŃĆéĶ»źń«Śµ│ĢńÜäÕ¤║µ£¼µĆصā│µś»ķĆÜĶ┐ćĶ«Īń«Śńø┤ń║┐ńÜäµ¢£ńÄćÕÆīµł¬ĶĘØµØź...
µĀ╣µŹ«µÅÉõŠøńÜäµ¢ćõ╗Čõ┐Īµü»’╝īµłæõ╗¼ÕÅ»õ╗źµĘ▒ÕģźµÄóĶ«©Ķ«Īń«Śµ£║ÕøŠÕĮóÕŁ”õĖŁńÜäÕćĀõĖ¬µĀĖÕ┐āń«Śµ│Ģ’╝Üńø┤ń║┐ńö¤µłÉń«Śµ│ĢŃĆüÕ£åńö¤µłÉń«Śµ│ĢŃĆüµżŁÕ£åńö¤µłÉń«Śµ│Ģõ╗źÕÅŖÕē¬ĶŻüń«Śµ│ĢŃĆéĶ┐Öõ║øń«Śµ│ĢÕ£©Ķ«Īń«Śµ£║ÕøŠÕĮóÕŁ”ķóåÕ¤¤µ£ēńØĆÕ╣┐µ│øńÜäÕ║öńö©’╝īõĖŹõ╗ģķĆéńö©õ║ÄńÉåĶ«║ńĀöń®Č’╝īĶ┐śÕ╣┐µ│øńö©õ║ÄĶĮ»õ╗ČÕ╝ĆÕÅæŃĆü...
CĶ»ŁĶ©ĆÕ«×ńÄ░Bresenhamńø┤ń║┐ńö¤µłÉń«Śµ│ĢÕÅ»ĶāĮÕ”éõĖŗ’╝Ü ```c #include // ÕüćĶ«Šµłæõ╗¼µ£ēõĖĆõĖ¬õ║īń╗┤µĢ░ń╗äõ╗ŻĶĪ©Õ▒ÅÕ╣Ģ’╝ī(0,0)õĖ║ÕĘ”õĖŖĶ¦Æ int screen[800][600]; void draw_line(int x0, int y0, int x1, int y1) { int dx = abs(x1 - x0...
µĆ╗ńÜäµØźĶ»┤’╝īĶ«Īń«Śµ£║ÕøŠÕĮóÕŁ”õĖŁńÜäńø┤ń║┐ÕÆīÕ£åńö¤µłÉń«Śµ│Ģµś»ķĆÜĶ┐ćÕ»╣ńé╣ŃĆüÕāÅń┤ĀÕÆīµĢ░ÕŁ”Õģ│ń│╗ńÜäńÉåĶ¦ŻµØźÕ«×ńÄ░ńÜäŃĆéÕ£©Õ«×ķÖģÕ║öńö©õĖŁ’╝īµłæõ╗¼ķ£ĆĶ”üµĀ╣µŹ«õĖŹÕÉīńÜäµāģÕåĄķĆēµŗ®ÕÉłķĆéńÜäń«Śµ│Ģ’╝īõ╗źĶŠŠÕł░ńÉåµā│ńÜäĶ¦åĶ¦ēµĢłµ×£ŃĆéķÜÅńØĆńĪ¼õ╗ȵƦĶāĮńÜäµÅÉÕŹćÕÆīµ¢░ńÜäÕøŠÕĮóÕżäńÉåµŖƵ£»ńÜäÕÅæÕ▒Ģ...
Õ£©Ķ«Īń«Śµ£║ÕøŠÕĮóÕŁ”õĖŁ’╝īń║┐µ«ĄńÜäń╗śÕłČķĆÜÕĖĖķććńö©Bresenhamń«Śµ│Ģµł¢DDA’╝łDigital Differential Analyzer’╝ēń«Śµ│Ģ’╝īĶ┐Öõ║øń«Śµ│ĢĶāĮķ½śµĢłÕ£░Õ£©ÕāÅń┤Āń║¦Õł½õĖŖĶ┐æõ╝╝Õć║ńø┤ń║┐ŃĆé õ║īŃĆüÕ£åõĖĵżŁÕ£å Õ£åÕÆīµżŁÕ£åńÜäĶĪ©ńż║ķĆÜÕĖĖÕ¤║õ║ĵ×üÕØɵĀ浳¢ĶĆģÕÅéµĢ░µ¢╣ń©ŗŃĆéõŠŗÕ”é’╝īÕÅ»õ╗ź...
Ķ┐Öµ«ĄµŚČķŚ┤Õ╝äõ║åÕŠłÕżÜÕøŠÕĮóÕŁ”µ¢╣ķØóńÜäń«Śµ│Ģ’╝īÕ”éDDAńö╗ńø┤ń║┐ń«Śµ│Ģ’╝īõ╗źÕÅŖMidpointLineŃĆüBresenhamLineŃĆüĶ┐śµ£ēńö╗Õ£åńÜäBresenhamCircleŃĆüMidpointCircleõ╗źÕÅŖÕżÜń¦Ź ń¦ŹÕŁÉÕĪ½Õģģń«Śµ│Ģ’╝īÕ”éFloodfillŃĆüScanlineSeedfillŃĆüETĶŠ╣ĶĪ©ńÜä Polygonfill...
ńö╗ńø┤ń║┐ÕÆīµŖśń║┐µś»Ķ«Īń«Śµ£║ÕøŠÕĮóÕŁ”ńÜäķćŹĶ”üÕåģÕ«╣’╝īõ║åĶ¦Żńö╗ńø┤ń║┐ÕÆīµŖśń║┐ńÜäń«Śµ│ĢÕÆīÕ«×ńÄ░µ¢╣µ│Ģµś»ÕŁ”õ╣ĀÕøŠÕĮóÕŁ”ńÜäÕ┐ģÕżćµØĪõ╗ČŃĆéńö╗ńø┤ń║┐ńÜäń«Śµ│ĢÕīģµŗ¼DDAń«Śµ│ĢŃĆüBresenhamń«Śµ│ĢńŁē’╝īńö╗µŖśń║┐ńÜäń«Śµ│ĢÕīģµŗ¼B-splineń«Śµ│ĢŃĆüBezierµø▓ń║┐ń«Śµ│ĢńŁēŃĆé ńö╗Õ╝¦ń║┐ÕÆīµø▓ń║┐ ...
µĆ╗ń╗ōµØźĶ»┤’╝īńø┤ń║┐µ«ĄĶŻüÕē¬µś»Ķ«Īń«Śµ£║ÕøŠÕĮóÕŁ”õĖŁńÜäÕ¤║µ£¼µŖƵ£»’╝īķĆÜĶ┐ćÕÉäń¦Źń«Śµ│ĢÕ«×ńÄ░Õ»╣ÕøŠÕĮóÕģāń┤ĀńÜ䵜Šńż║µÄ¦ÕłČŃĆéĶ┐Öõ║øń«Śµ│ĢńÜäńÉåĶ¦ŻÕÆīµÄīµÅĪÕ»╣õ║ĵĘ▒ÕģźÕŁ”õ╣ĀĶ«Īń«Śµ£║ÕøŠÕĮóÕŁ”Ķć│Õģ│ķćŹĶ”ü’╝īÕ«āõ╗¼µ×䵳Éõ║åńÄ░õ╗ŻÕøŠÕĮóÕ║öńö©ń©ŗÕ║ÅńÜäÕ¤║ńĪĆŃĆéķĆÜĶ┐ćńøĖõ║ÆÕŁ”õ╣ĀÕÆīõĖŹµ¢ŁµÅÉķ½ś’╝ī...