Ø 总体概述
模糊数学已经使用到各个领域,其在图像的分割中也是常用的经典方法,而且实时在其基础上能有些创新。本文通过两天来对模糊数学基础知识学习进行个小的poject巩固。本文标题兼主要内容为基于模糊等价关系的模糊聚类程序实现。
为什么要把模糊聚类分析基于模糊等价关系之上呢?模糊等价关系是同时满足自反性、对称性和传递性的模糊关系,因此必定有如下特性:
(1)自反性:保证关系中元素和元素本身是同一类
(2)对称性:保证元素A与B同类,则B与A也同类
(3)传递性:若A与B同类,B与C同类,则A与C同类
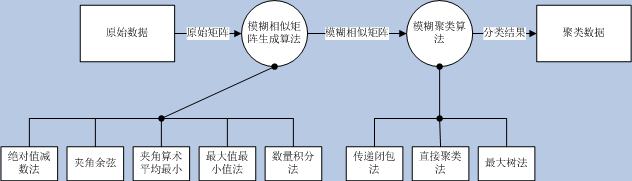
一般的聚类分析流程图如下
%作者:夏侯佐鑫
%日期:2012-07-15
%功能:模糊聚类分析
clc
% 1)原始矩阵
disp('1)原始矩阵')
A = [5 5 3 2;
2 3 4 5;
5 5 2 3;
1 5 3 1;
2 4 5 1]
% 2)计算相似矩阵M
disp('2)计算相似矩阵M')
M = abs_sub(A, 5, 4)
% 3)计算模糊等价矩阵
disp('3)计算模糊等价矩阵')
N = matrix_com(M, 5)
% 4)λ聚类分析
r = 0.4;
sprintf('4)λ聚类分析(λ=%0.1f)', r)
Q = cluster(N, r)
Ø 下面分步骤实现每个过程中的调用函数
(1)获取原始矩阵
|
地方
|
空气
|
水
|
土壤
|
植被
|
|
A
|
5
|
5
|
3
|
2
|
|
B
|
2
|
3
|
4
|
5
|
|
C
|
5
|
5
|
2
|
3
|
|
D
|
1
|
5
|
3
|
1
|
|
E
|
2
|
4
|
5
|
1
|
由上表很容易一一对应获得矩阵
A = [5 5 3 2;
2 3 4 5;
5 5 2 3;
1 5 3 1;
2 4 5 1]
矩阵的行代表对象,矩阵的列代表对象具有的性质。
(2)计算相似矩阵
方法很多,这里使用很简单的绝对值减法,其数学公式如下
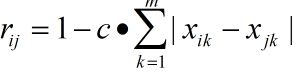
代表相似矩阵中的第i行第j列元素,代表A矩阵的第i行第j列元素。
%作者:夏侯佐鑫
%日期:2012-07-15
%功能:绝对值减数法计算相对矩阵
function y = abs_sub(array, m, n);
% array - Input array original array
% m - number of objects
% n - number of properties
c = 0.1;
temp = 0;
for i = 1:m
for j = 1:m
for k = 1:n
temp = temp + abs(array(i,k)-array(j,k));
end
y(i,j) = 1 - c*temp;
temp = 0;
end
end
(3)计算模糊等价矩阵
这里利用离散数学里面的关系的合成运算方法,通过迭代计算等价矩阵。
%作者:夏侯佐鑫
%日期:2012-07-15
%功能:模糊矩阵合成计算传递闭包
function y = matrix_com(array, m);
% array - Input array original array
% m - number of objects
% n - number of properties
flag = 0;%是否找到传递闭包的标志
temp = 0;
cnt = 0;
while ~flag
y = temp;
for i=1:m
for j=1:m
temp(i,j) = 0;
for k=1:m
if cnt==0
temp(i,j)=max(temp(i,j),min(array(i,k), array(k,j)));
else
temp(i,j)=max(temp(i,j),min(y(i,k), y(k,j)));
end
end
end
end
cnt = cnt + 1;
if y == temp
flag = 1;%传递闭包已找到
end
end
(4)截值聚类分析
很简单,比如有矩阵
A = [5 5 3 2;
2 3 4 5;
5 5 2 3;
1 5 3 1;
2 4 5 1]
使用截值r=3,则将A矩阵中比3小的值置0,大于等于3的值置1。结果为
A = [1 1 1 0;
0 1 1 1;
1 1 0 1;
0 1 1 0;
0 1 1 0]
使用简单的matlab程序实现如下
%作者:夏侯佐鑫
%日期:2012-07-15
%功能:λ聚类分析
function y = cluster(array, r);
% array -模糊相似矩阵或模糊等价矩阵
% r -聚类截距
if r>1 | r<0
error('第二个参数必须小于1');
end
len = length(array);
for i=1:len
for j=1:len
if array(i,j)>=r
y(i,j) = 1;
else
y(i,j) = 0;
end
end
end
Ø
最后通过matlab输出结果进一步认识整个模糊聚类的过程
1)原始矩阵
A =
5 5 3 2
2 3 4 5
5 5 2 3
1 5 3 1
2 4 5 1
2)计算相似矩阵M
M =
1 1/10 4/5 1/2 3/10
1/10 1 1/10 1/5 2/5
4/5 1/10 1 3/10 1/10
1/2 1/5 3/10 1 3/5
3/10 2/5 1/10 3/5 1
3)计算模糊等价矩阵
N =
1 2/5 4/5 1/2 1/2
2/5 1 2/5 2/5 2/5
4/5 2/5 1 1/2 1/2
1/2 2/5 1/2 1 3/5
1/2 2/5 1/2 3/5 1
4)λ聚类分析(λ=0.6)
Q =
1 0 1 0 0
0 1 0 0 0
1 0 1 0 0
0 0 0 1 1
0 0 0 1 1
所以,当r=0.6时,最终分类结果为{A,C},{D,E},{B,C}三组。选择不同的r值得到不同的分类结果。
分享到:









相关推荐
论文研究-基于模糊邻近关系的结构聚类.pdf, 在有序粒度空间理论的基础上, 提出了基于模糊邻近关系的结构聚类分析理论和方法. 首先, 给出了依据距离的一致聚类的概念, ...
研究者们通过实例验证了基于语言变量的区间二型模糊等价关系聚类分析新算法的可行性,证实了该方法在处理不确定性问题方面的能力,相较于传统模糊聚类算法,它能够获得更精确的聚类结果,并且具有更广阔的应用空间。...
总结起来,模糊聚类是一个处理不确定性和模糊性数据的有效工具,其中标准化确保了数据的公平比较,模糊相似矩阵捕捉了数据间的模糊关系,而模糊等价矩阵则帮助构建了模糊聚类的结构。这些概念和算法在诸如图像分析、...
论文研究-基于区间二型模糊集的模糊等价关系聚类分析.pdf, 传统聚类算法在解决含有不确定性的聚类问题时具有很大的局限性,为了更好地解决聚类问题中的不确定性,论文基于...
基于模糊等价关系的聚类分析是模糊数学的一个重要应用领域,它能够更有效地处理那些边界不清晰、类别归属不确定的数据集。 在模糊聚类分析中,通常会涉及以下关键步骤: 1. **数据矩阵的建立**:首先,需要将待...
1)根据表格中的数据,用Matlab编程进行数据标准化处理; 2)根据标准化处理后的数据,用Matlab编程,建立模糊相似矩阵,并编程求出...3)根据模糊等价矩阵,编程绘制动态聚类图; 4)根据原始数据,编程确定最佳分类结果。
在这个“模糊聚类matlab程序”中,包含了使用不同聚类方法的实现,比如相关系数法和欧几里得法。 相关系数法聚类是基于变量间线性关系的一种聚类方式。在这种方法中,数据点之间的相似度通过计算它们与其他所有点的...
论文研究-基于摄动的模糊聚类算法最优模糊等价矩阵相关性质分析.pdf, 对基于摄动的模糊聚类算法进行深入研究.给出一个模糊相似矩阵的实例,存在与该矩阵距离相同且都是...
5. **进行模糊聚类分析**:基于得到的模糊等价关系进行聚类分析。 **2.2.2 模糊聚类分析的直接法** 直接法与间接法的主要区别在于,它不需要先求出模糊等价关系即可直接进行聚类分析。直接法的优势在于简化了分析...
针对模糊聚类方法中存在冗余信息的问题,提出一种融合粗糙集属性约简和模糊等价关系的故障诊断方法,通过应用粗糙集属性约简算法对冗余数据的处理后再应用模糊等价关系聚类获取聚类结果。该方法与单采用模糊等价关系...
首先引入直觉模糊集的模运算、直觉模糊集之间的关系及合成运算的定义,然后提出了直觉模糊集的截集定义,揭示了利用直觉模糊等价关系的分类原理,并讨论了基于直觉模糊等价关系的模糊聚类算法,从而使直觉模糊集的...
模糊综合评价与模糊聚类分析,作为模糊理论中最为重要的两个应用分支,在解决复杂实际问题方面展现了其独特的优势和潜力。 模糊理论的核心思想是通过模糊集合的概念来模拟现实世界的不确定性和模糊性。传统的集合论...
本篇文章将基于提供的文档内容——“matlab模糊聚类程序.doc”——来详细阐述模糊聚类的具体步骤及其在MATLAB中的实现过程。该文档主要包括三个核心步骤:数据标准化、建立模糊相似矩阵以及动态聚类图的构建。 ####...
2. **模糊聚类算法的实现途径**:探索高效的模糊聚类算法,提高计算效率。 3. **模糊聚类的应用研究**:将模糊聚类方法应用于不同领域,解决实际问题。 4. **模糊聚类有效性的研究**:评估模糊聚类算法的有效性,...
该方法首先利用基于模糊等价关系的模糊聚类和硬划分技术来求出样本的最佳分类,然后利用软划分技术进行迭代求解聚类中心。之后,通过模糊数学的模糊相似度理论进行预测,从而得出科学的评价结果,用于判断是否继续...