deepfuture
- 浏览: 4413039 次
- 性别:
- 来自: 湛江
-
博客专栏
-
-
SQLite源码剖析
浏览量：80136
-
-
WIN32汇编语言学习应用...
浏览量：70372
-
-
神奇的perl
浏览量：103610
-
-
lucene等搜索引擎解析...
浏览量：286603
-
-
深入lucene3.5源码...
浏览量：15056
-
-
VB.NET并行与分布式编...
浏览量：67829
-
-
silverlight 5...
浏览量：32293
-
-
算法下午茶系列
浏览量：46075
最新评论
-
yoyo837：
counters15 写道目前只支持IE吗？插件的东西是跨浏览 ...
Silverlight 5 轻松开启绚丽的网页3D世界 -
shuiyunbing：
直接在前台导出方式：excel中的单元格样式怎么处理，比如某行 ...
Flex导出Excel -
di1984HIT：
写的很好~
lucene入门-索引网页 -
rjguanwen：
在win7 64位操作系统下，pygtk的Entry无法输入怎 ...
pygtk-entry -
ldl_xz：
http://www.9958.pw/post/php_exc ...
PHPExcel常用方法汇总(转载)
，那么
。
。
：
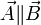
相关推荐
柯西-施瓦茨不等式（Cauchy-Schwarz Inequality）是线性代数和泛函分析中的一个基本不等式，它在高等数学中占据着重要的地位。这个不等式揭示了内积空间中两个向量之间长度的关系，具有广泛的应用，包括在解析几何、...
《柯西-施瓦茨大师课》这本书以柯西-施瓦茨不等式作为起点，通过一系列引人入胜的问题引导读者深入探索最基础的数学不等式。不等式是数学领域中的核心元素之一，在物理、数学、计算机科学等领域都有着广泛的应用。...
2. Cauchy-Schwarz不等式（柯西-施瓦茨不等式）则是线性代数中的一个重要结果，它表明对于所有实数向量x和y，有|x•y|²≤||x||²||y||²。在第10题中，直线方程＋＝1可以通过Cauchy-Schwarz不等式转化为关于2a＋b的...
基于Cauchy-Schwarz散度，提出了一种新的主动轮廓线图像分割模型。该模型能量泛函有两部分组成：几何正则项和数据拟合项。其中，数据拟合项通过图像灰度的概率密度函数之间的Cauchy-Schwarz散度来加以构造，并且对...
首先，柯西施瓦茨不等式（Cauchy-Schwarz Inequality）的基本形式为： 对于任何在某个区间上平方可积的函数f(x)和g(x)，都有 \[\left( \int_{a}^{b} f(x)g(x)dx \right)^2 \leq \left( \int_{a}^{b} f^2(x)dx \...
4. 第7题和第8题要求找到ab或a+b的取值范围，这需要用到基本不等式结合不等式性质，如Cauchy-Schwarz不等式（柯西-施瓦茨不等式），来确定表达式的上下界。 5. 题目的[B组]部分涉及更高层次的应用，如第1题中直线过...
首先，例题1中柯西-施瓦茨不等式的应用表明，对于实数x、y、z，表达式(x－1)²+(y+1)²+(z+1)²存在最小值，而这一最小值的寻找依赖于不等式性质的理解。柯西-施瓦茨不等式告诉我们，两个实数序列的点积的平方不大于...
本书不仅涵盖了经典的不等式理论，如舒尔不等式（Schur's inequality）、缪尔黑德定理（Muirhead's theorem）、柯西-施瓦茨不等式（Cauchy-Schwarz inequality）、算术平均-几何平均不等式（AM-GM inequality）以及...
4. **柯西-施瓦茨不等式（Cauchy-Schwarz 不等式）在证明中的应用**： 第四题中，利用柯西-施瓦茨不等式证明了 `(x-1)^2 + (y+2)^2 + (z-3)^2` 的最小值，这在处理向量或函数的平方和问题时非常常见。 5. **基本...
基本不等式主要包括AM-GM不等式（算术平均-几何平均不等式）和Cauchy-Schwarz不等式（柯西-施瓦茨不等式），它们在解决最值问题和求取值范围时起到关键作用。 1. AM-GM不等式：这个不等式表述为，对于任何非负实数a...
不等式的种类繁多，包括基本不等式、AM-GM不等式、柯西-施瓦茨不等式等，每一类不等式都有其独特的应用背景和证明方法。基本不等式是解决不等式问题的基础，它涉及到变量间的大小关系，以及如何通过代数操作来变换...
2. **柯西-施瓦茨不等式（Cauchy-Schwarz 不等式）**：在实数或复数向量空间中，对于任何两个向量a和b，其标量积的绝对值不大于它们模的乘积，即|, b>|² ≤ |a|² * |b|²。这个不等式在处理线性代数问题，特别是...
4. 柯西-施瓦茨不等式：在证明 x2+112 x1 和 22322xx 这样的不等式时，可能会用到柯西-施瓦茨不等式（Cauchy-Schwarz不等式）。 5. 不等式的应用：例如求证 9111cba 当 a+b+c=1 时，这是基本不等式...
- 在证明 `(1)` 和 `(2)` 部分中，使用了柯西-施瓦茨不等式 $(a^2+b^2)(c^2+d^2)\geq (ac+bd)^2$，这在处理平方和与乘积关系时非常有用。不等式 `(1)` 证明了如果$ab > cd$，那么$\sqrt{a}+\sqrt{b} > \sqrt{c}+\...
9. 求和式938432abcbccaab的最小值，可能需要利用AM-GM不等式或者柯西-施瓦茨不等式。 10. 正实数x, y满足特定条件，求解x+的最值。需要考虑不等式和函数的性质。 11. 已知正实数的对数关系，求解表达式...
本书的一个重要章节聚焦于经典的不等式，包括算术平均数-几何平均数（AM-GM）不等式和柯西-施瓦茨不等式（Cauchy-Schwarz inequality）。AM-GM不等式是基础数学竞赛知识之一，它断言两个非负实数的算术平均数总是...
常见的基本不等式如AM-GM不等式（算术平均-几何平均不等式）和Cauchy-Schwarz不等式（柯西-施瓦茨不等式）在证明某些不等式时非常有用。例2中就使用了基本不等式。 6. 排序不等式（排序原理）： 排序不等式指出，...
再来看定理3，这可能涉及到了不等式的其他形式，如柯西-施瓦茨不等式（Cauchy-Schwarz不等式），它是线性代数和泛函分析中的基本工具。该不等式指出，对于任意长度为n的实数或复数序列\(a_1, a_2, ..., a_n\)和\(b_1...
4. 柯西-施瓦茨不等式（Cauchy-Schwarz Inequality）： 在文档的最后部分，柯西-施瓦茨不等式被提出，并被用于描述信号和参考向量之间关系的数学原理。该不等式在数学和工程学中是一个基础定理，指出在内积空间中，...
"Newton-Cotes quadrature"（牛顿-科特斯求积法），"Jordan"（若尔当矩阵），"Jacobi method"（雅可比方法），"Runge-Kutta method"（龙格-库塔方法），以及"Cauchy-Schwarz inequality"（柯西-施瓦茨不等式）等。...