OpenGL Projection Matrix
Related Topics: OpenGL Transformation
Overview
A computer monitor is a 2D surface. We need to transform 3D scene into 2D image in order to display it. GL_PROJECTION matrix is for this projection transformation . This matrix is used for converting from the eye coordinates to the clip coordinates. Then, this clip coordinates are also transformed to the normalized device coordinates (NDC) by divided with w component of the clip coordinates.
Therefore, we have to keep in mind that both clipping and NDC transformations are integrated into GL_PROJECTION matrix. The following sections describe how to build the projection matrix from 6 parameters; left , right , bottom , top , near and far boundary values.
Perspective Projection
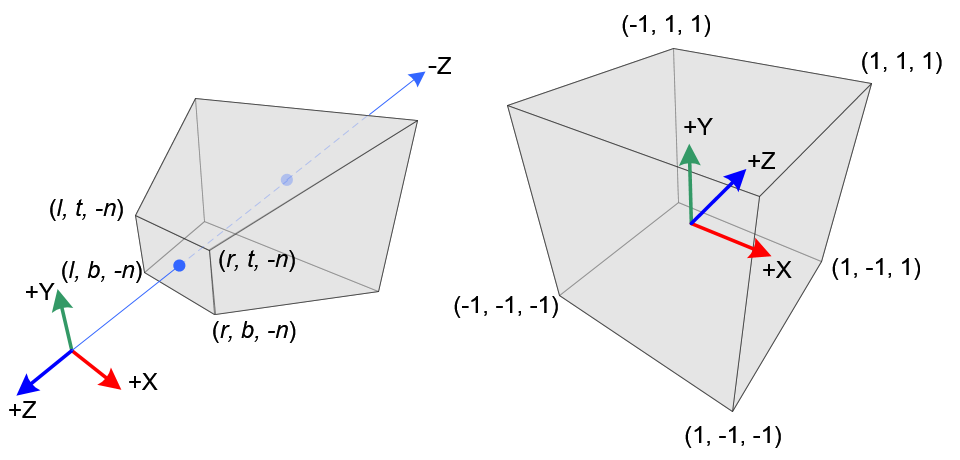 Perspective Frustum and Normalized Device Coordinates (NDC)
Perspective Frustum and Normalized Device Coordinates (NDC)
In perspective projection, a 3D point in a truncated pyramid frustum (eye coordinates) is mapped to a cube (NDC); the x-coordinate from [l, r] to [-1, 1], the y-coordinate from [b, t] to [-1, 1] and the z-coordinate from [n, f] to [-1, 1].
Note that the eye coordinates are defined in right-handed coordinate system, but NDC uses left-handed coordinate system. That is, the camera at the origin is looking along -Z axis in eye space, but it is looking along +Z axis in NDC. Since glFrustum() accepts only positive values of near and far distances, we need to negate them during construction of GL_PROJECTION matrix.
In OpenGL, a 3D point in eye space is projected onto the near plane (projection plane). The following diagrams shows how a point (xe , ye , ze ) in eye space is projected to (xp , yp , zp ) on the near plane.
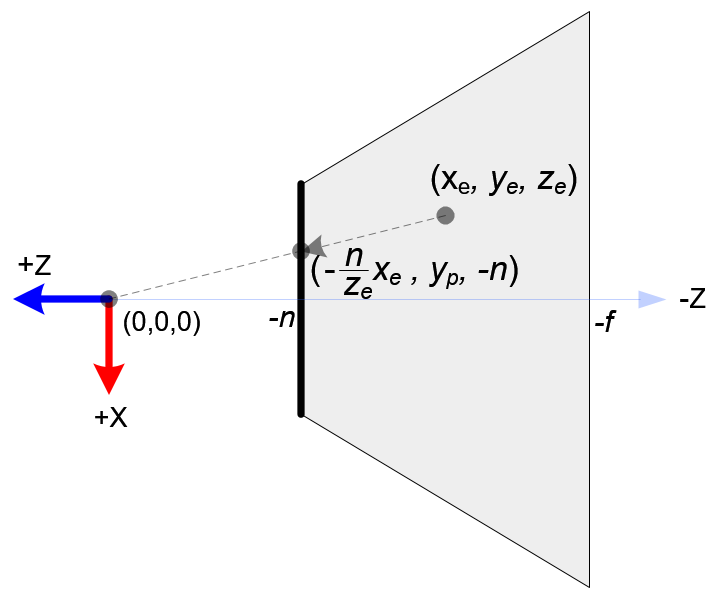 Top View of Projection
Top View of Projection
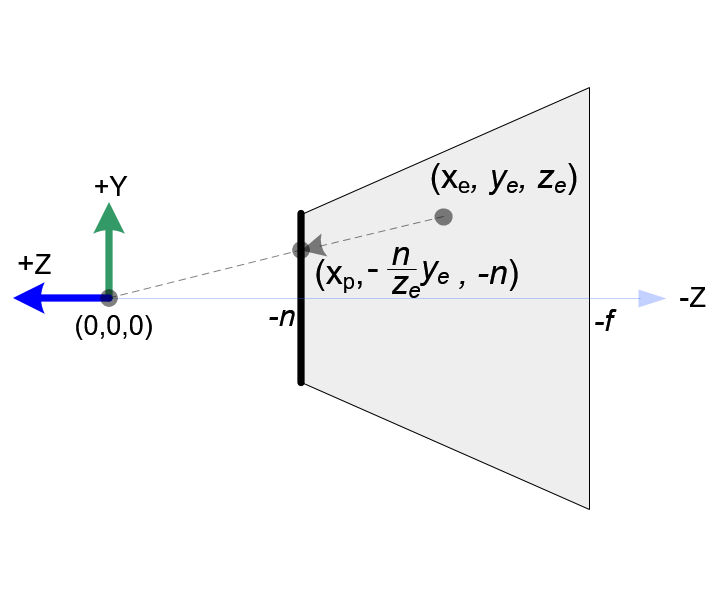 Side View of Projection
Side View of Projection
From the top view of the projection, the x-coordinate of eye space, xe is mapped to xp , which is calculated by using the ratio of similar triangles;
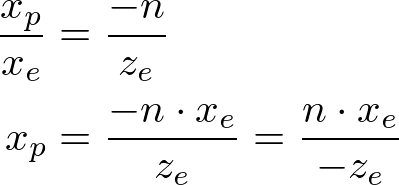
From the side view of the projection, yp is also calculated in a similar way;
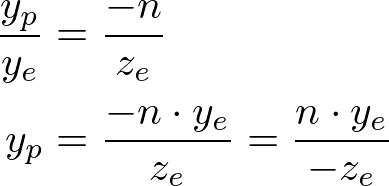
Note that both xp and yp depend on ze ; they are inversely propotional to -ze . It is an important fact to construct GL_PROJECTION matrix. After an eye coordinates are transformed by multiplying GL_PROJECTION matrix, the clip coordinates are still a homogeneous coordinates . It finally becomes normalized device coordinates (NDC) divided by the w-component of the clip coordinates. (See more details on OpenGL Transformation . )
 ,
, 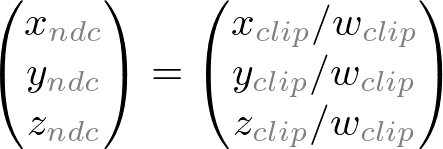
Therefore, we can set the w-component of the clip coordinates as -ze . And, the 4th of GL_PROJECTION matrix becomes (0, 0, -1, 0).
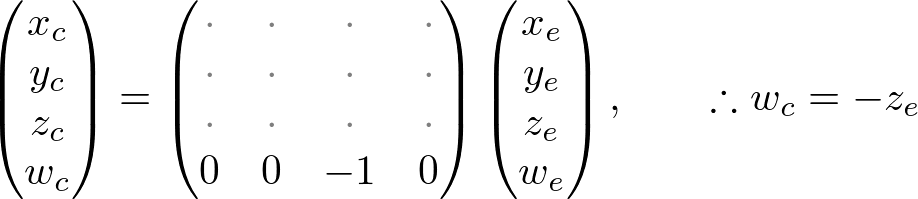
Next, we map xp and yp to xn and yn of NDC with linear relationship; [l, r] ⇒ [-1, 1] and [b, t] ⇒ [-1, 1].
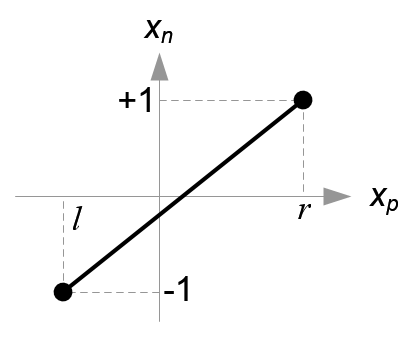 Mapping from xp to xn
Mapping from xp to xn
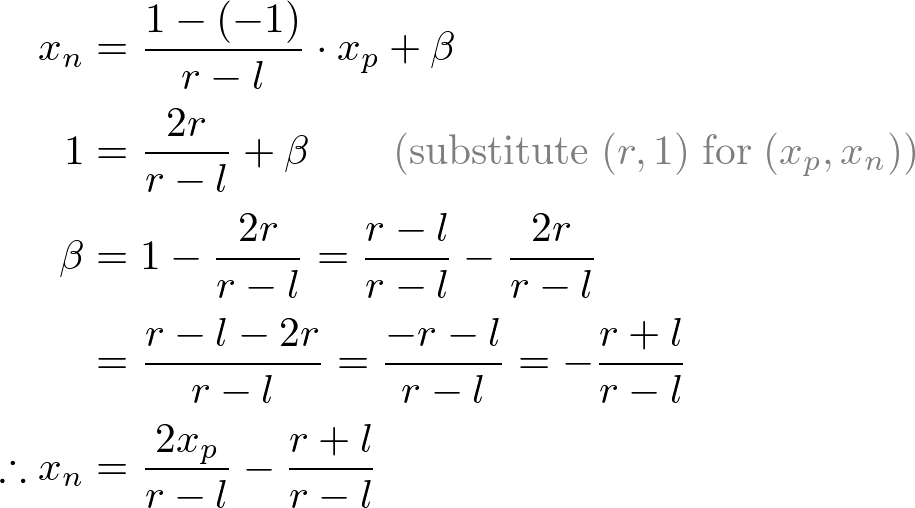
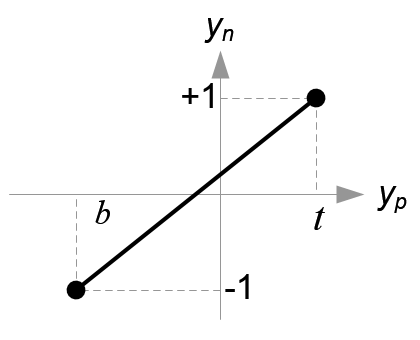 Mapping from yp to yn
Mapping from yp to yn
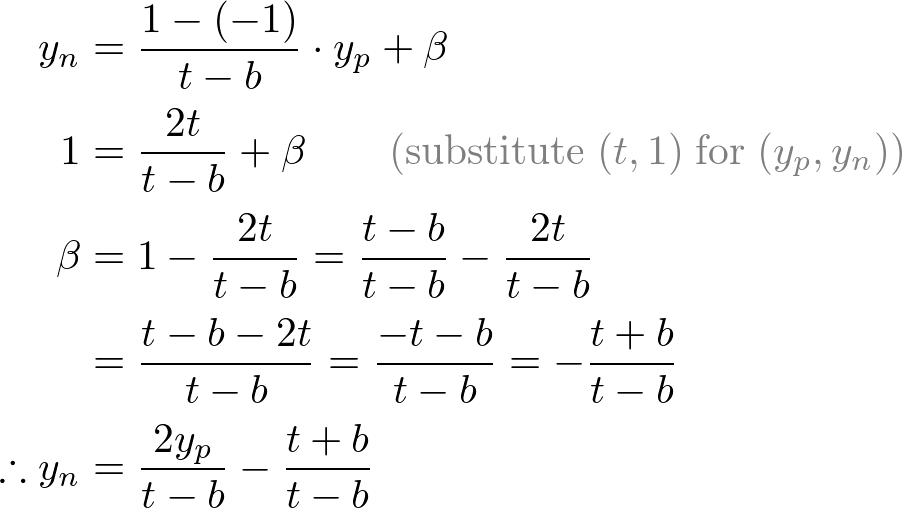
Then, we substitute xp and yp into the above equations.
Note that we make both terms of each equation divisible by -ze for perspective division (xc /wc , yc /wc ). And we set wc to -ze earlier, and the terms inside parentheses become xc and yc of clip coordiantes.
From these equations, we can find the 1st and 2nd rows of GL_PROJECTION matrix.
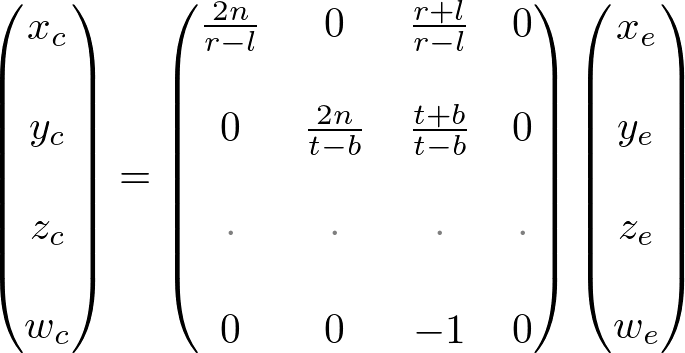
Now, we only have the 3rd row of GL_PROJECTION matrix to solve. Finding zn is a little different from others because ze in eye space is always projected to -n on the near plane. But we need unique z value for clipping and depth test. Plus, we should be able to unproject (inverse transform) it. Since we know z does not depend on x or y value, we borrow w-component to find the relationship between zn and ze . Therefore, we can specify the 3rd row of GL_PROJECTION matrix like this.
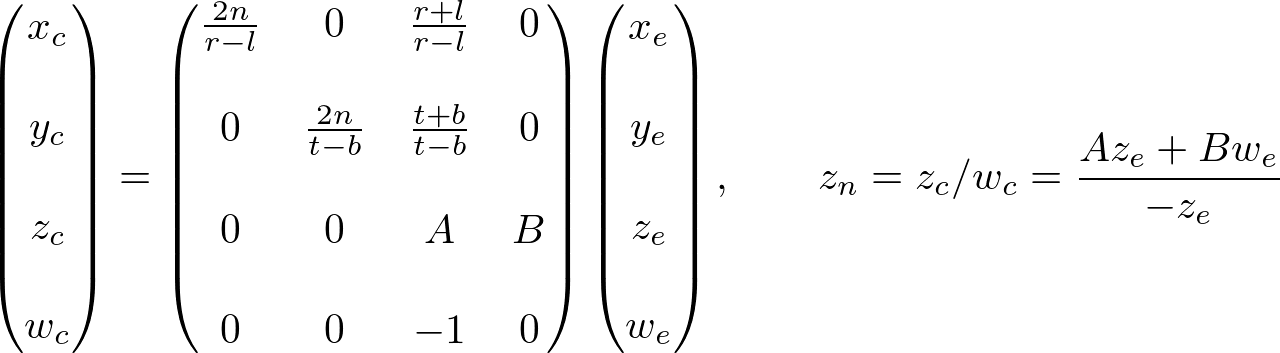
In eye space, we equals to 1. Therefore, the equation becomes;
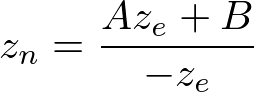
To find the coefficients, A and B , we use (ze , zn ) relation; (-n, -1) and (-f, 1), and put them into the above equation.
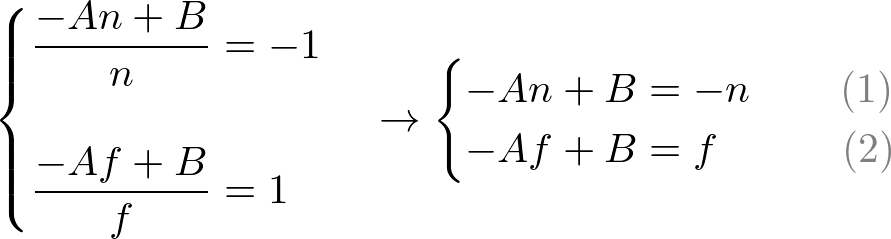
To solve the equations for A and B , rewrite eq.(1) for B;
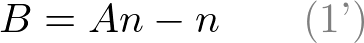
Substitute eq.(1') to B in eq.(2), then solve for A;
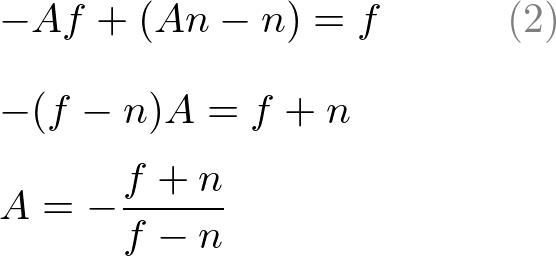
Put A into eq.(1) to find B ;
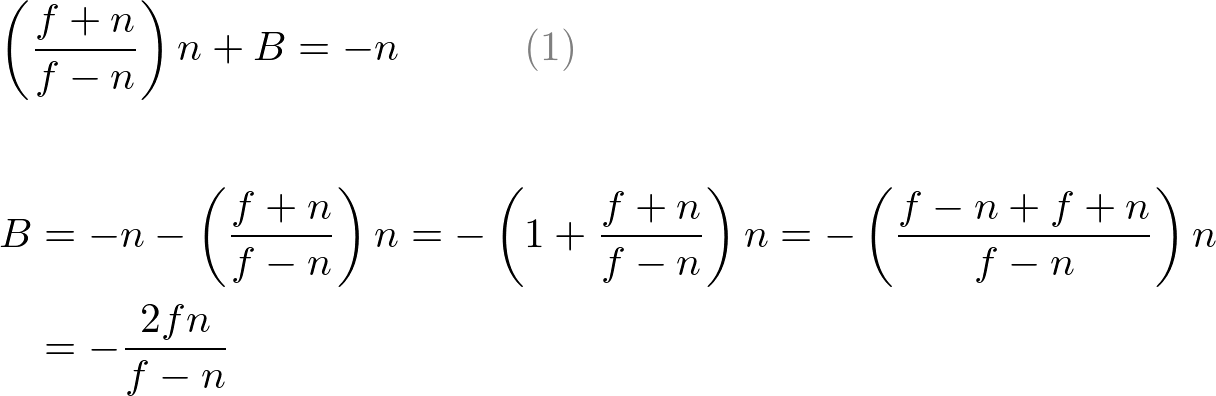
We found A and B . Therefore, the relation between ze and zn becomes;
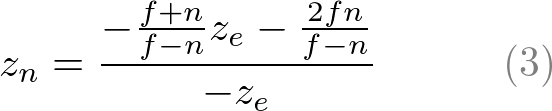
Finally, we found all entries of GL_PROJECTION matrix. The complete projection matrix is;
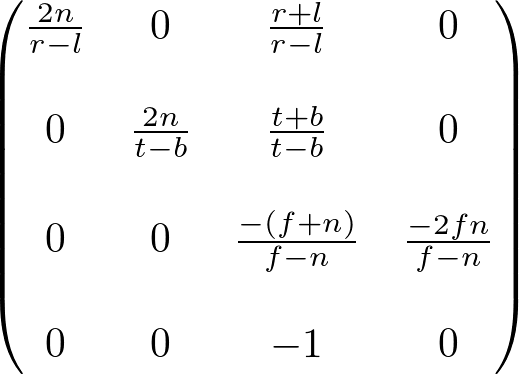
OpenGL Perspective Projection Matrix
This projection matrix is for general frustum. If the viewing volume is symmetric, which is 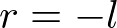 and
and 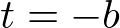 ,.then it can be simplified as;
,.then it can be simplified as;
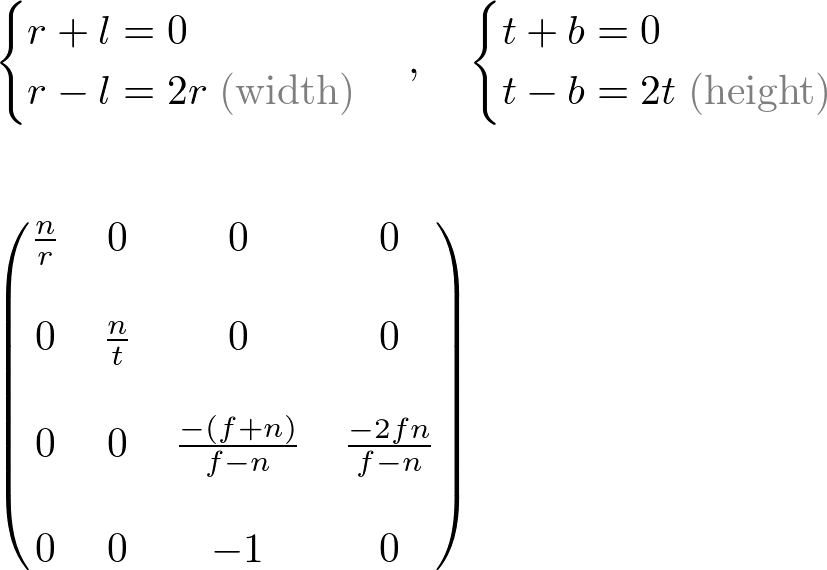
Before we move on, please take a look at the relation between ze and zn , eq.(3) once again. You notice it is a rational function and is non-linear relationship between ze and zn . It means there is very high precision at the near plane, but very little precision at the far plane. If the range [-n, -f] is getting larger, it causes a depth precision problem (z-fighting); a small change of ze around the far plane does not affect on zn value. The distance between n and f should be short as possible to minimize the depth buffer precision problem.
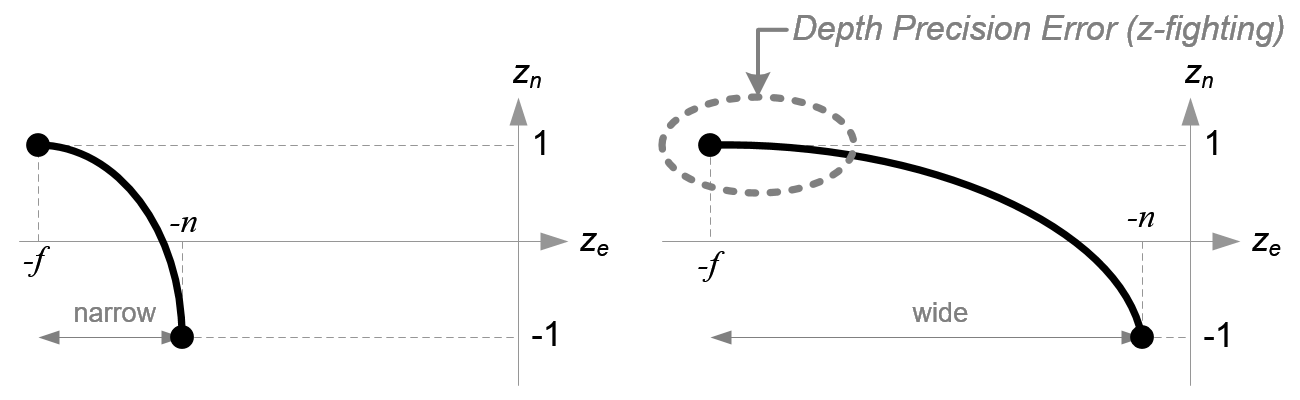 Comparison of Depth Buffer Precisions
Comparison of Depth Buffer Precisions
Orthographic Projection
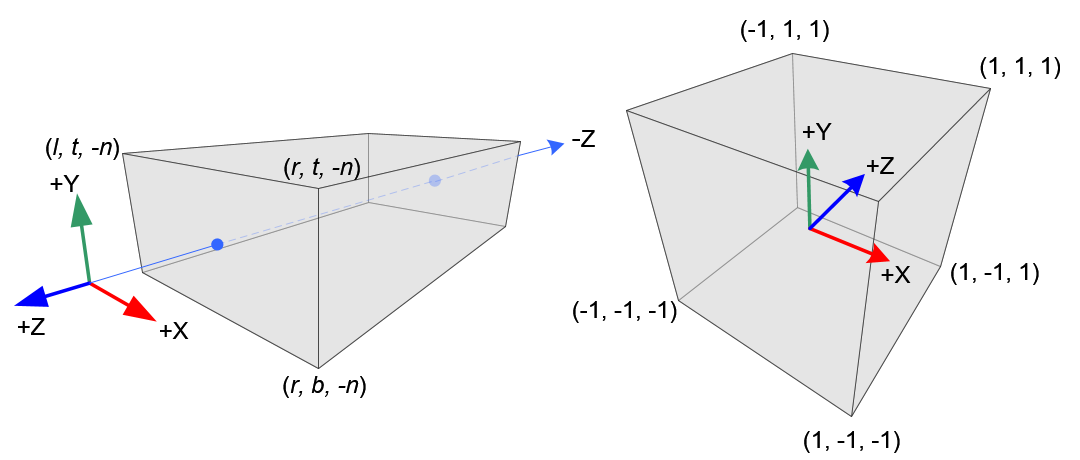 Orthographic Volume and Normalized Device Coordinates (NDC)
Orthographic Volume and Normalized Device Coordinates (NDC)
Constructing GL_PROJECTION matrix for orthographic projection is much simpler than perspective mode.
All xe , ye and ze components in eye space are linearly mapped to NDC. We just need to scale a rectangular volume to a cube, then move it to the origin. Let's find out the elements of GL_PROJECTION using linear relationship.
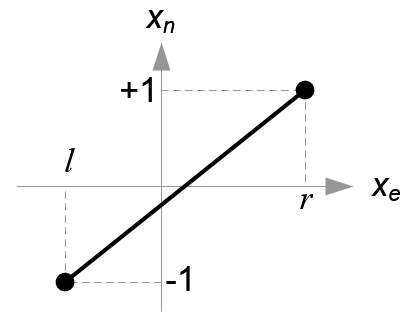 Mapping from xe to xn
Mapping from xe to xn
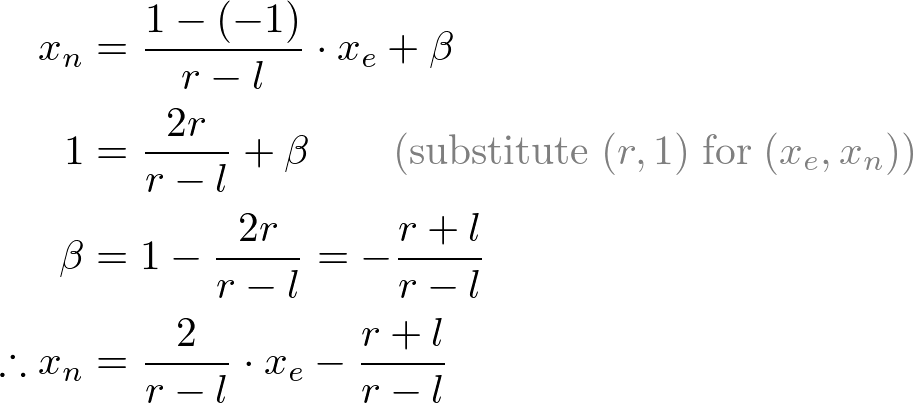
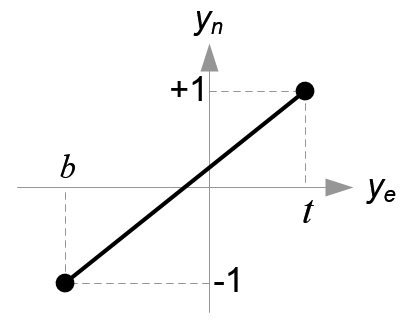 Mapping from ye to yn
Mapping from ye to yn
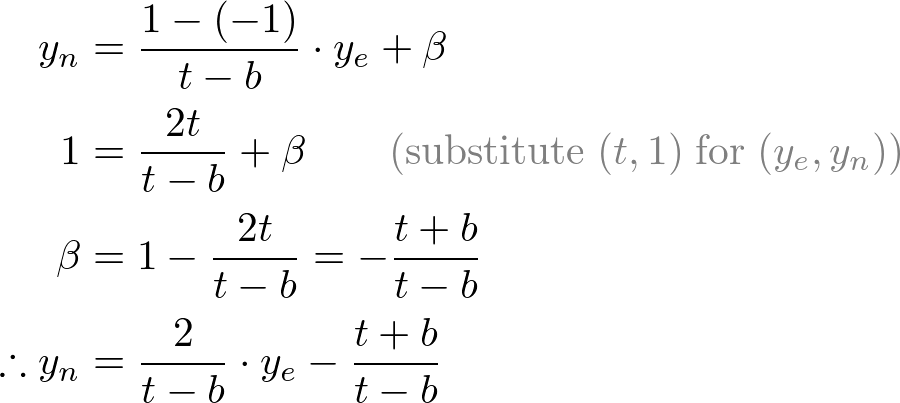
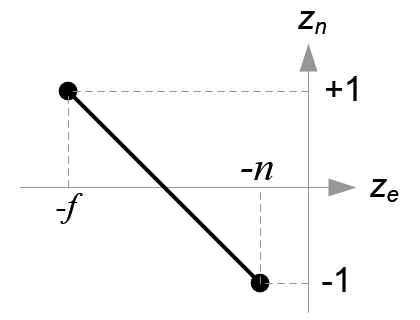 Mapping from ze to zn
Mapping from ze to zn
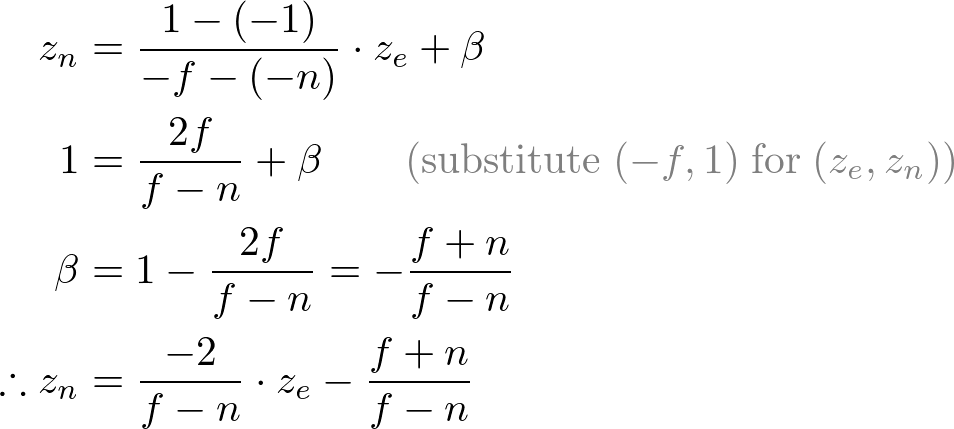
Since w-component is not necessary for orthographic projection, the 4th row of GL_PROJECTION matrix remains as (0, 0, 0, 1). Therefore, the complete GL_PROJECTION matrix for orthographic projection is;
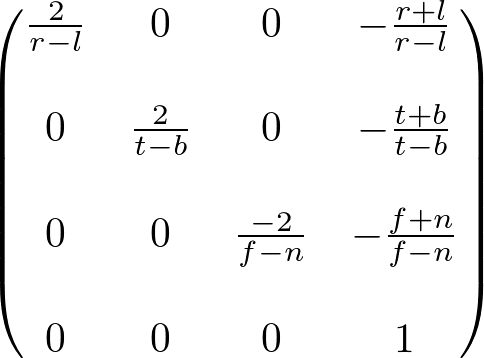
OpenGL Orthographic Projection Matrix
It can be further simplified if the viewing volume is symmetrical, 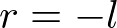 and
and 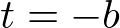 .
.
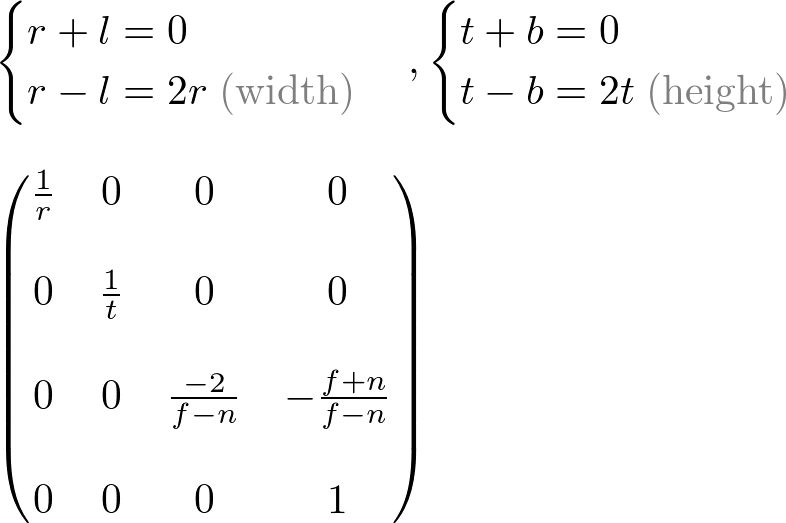
分享到:










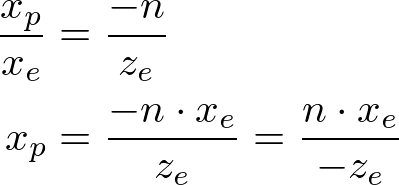
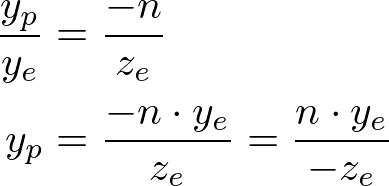

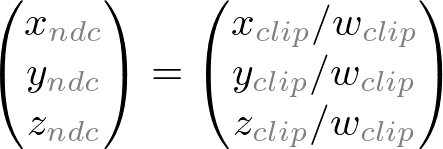
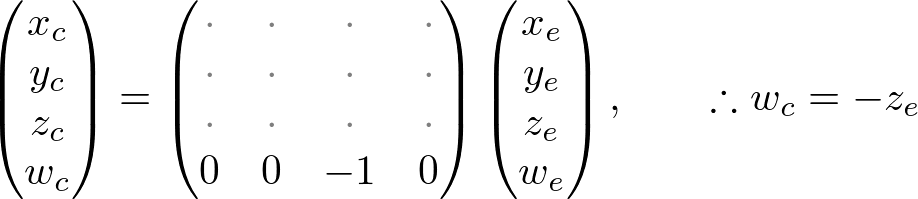

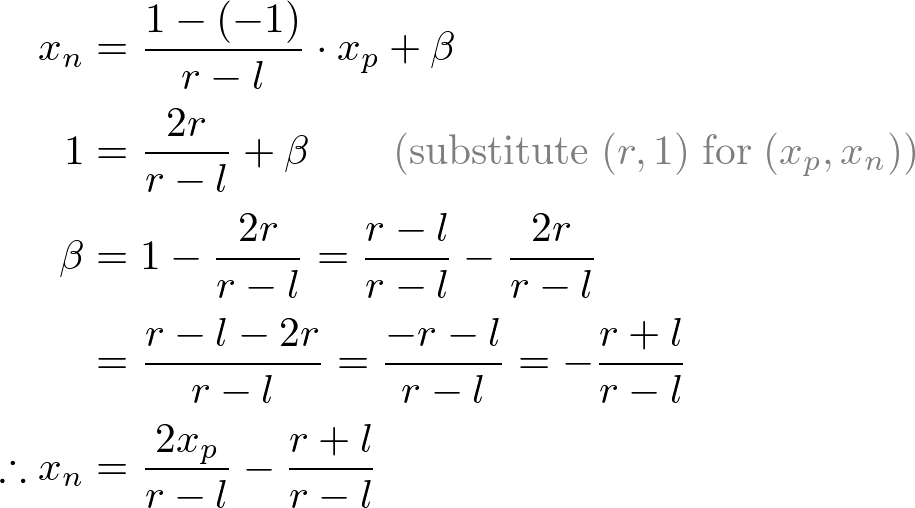

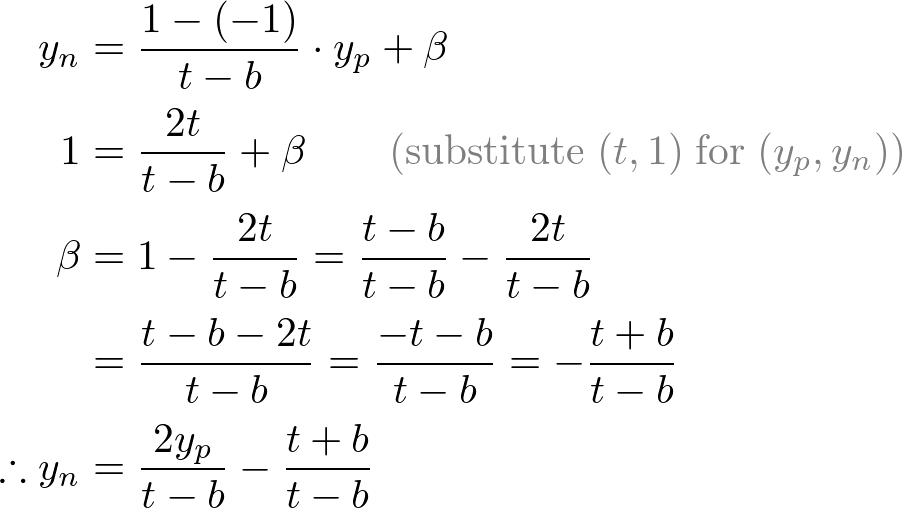
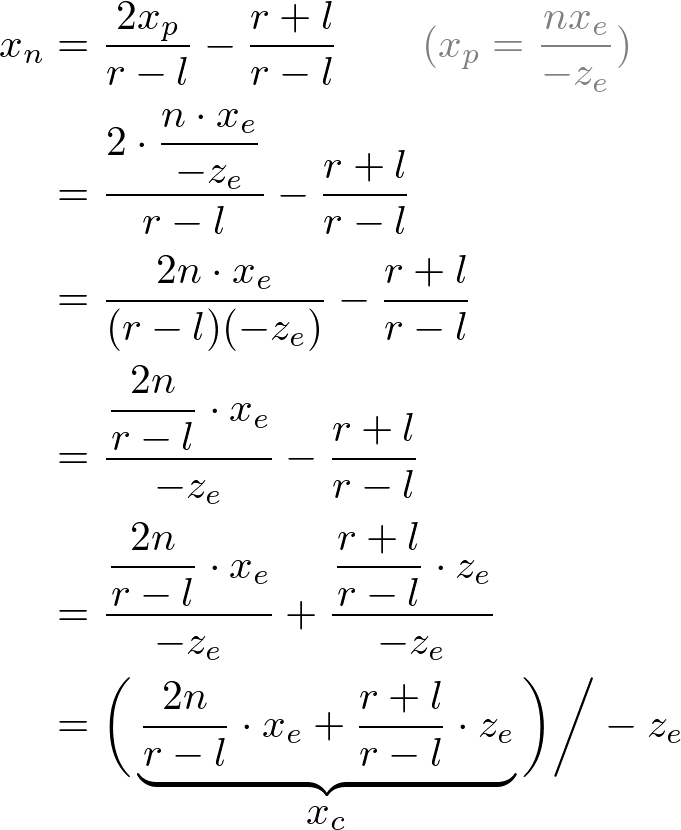
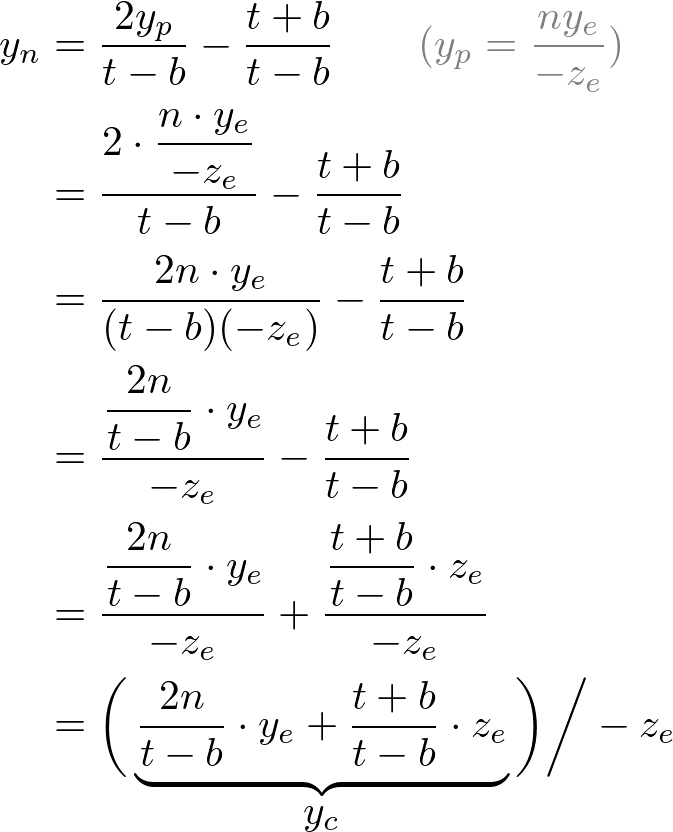
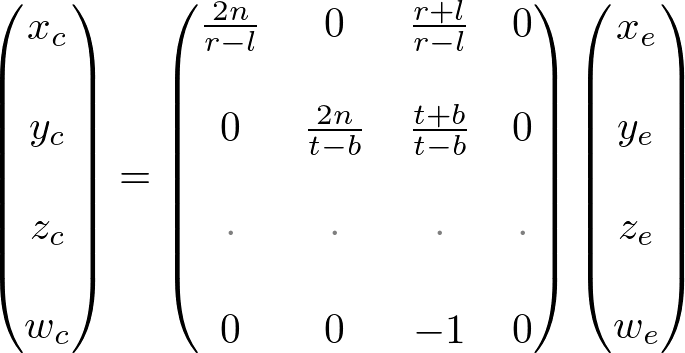
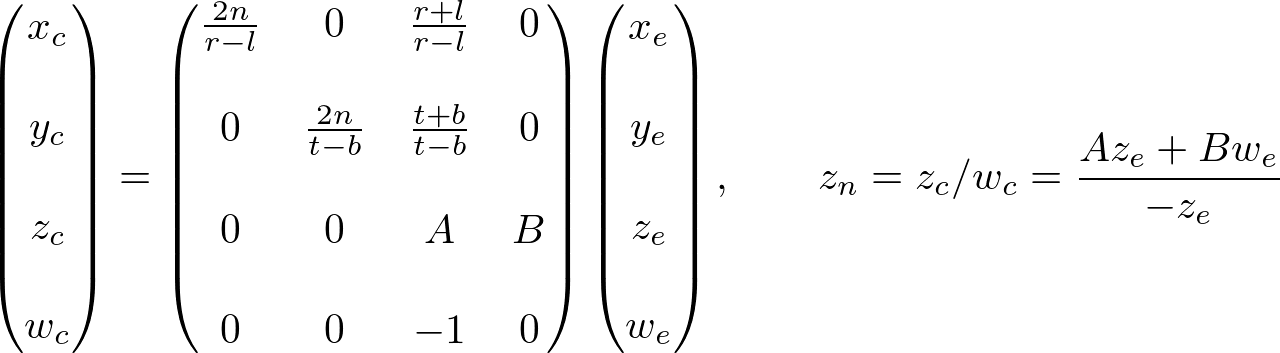
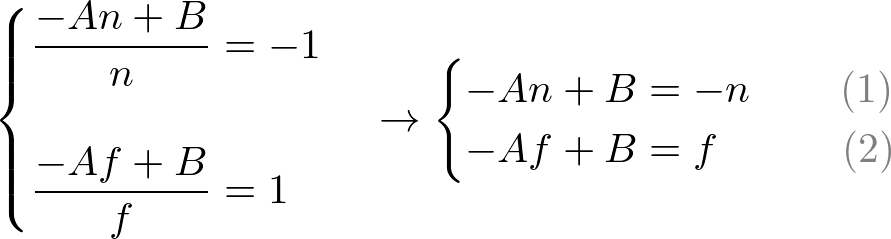
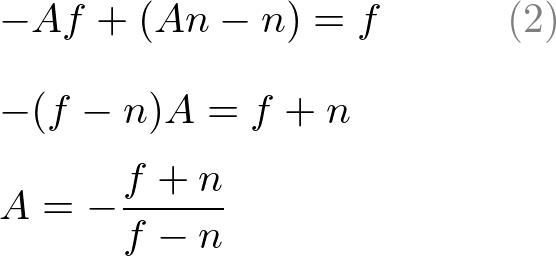
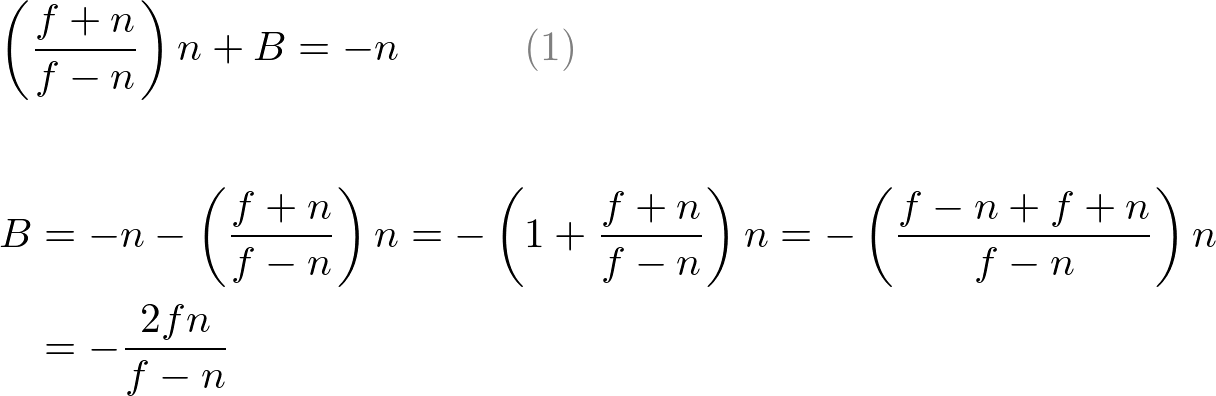
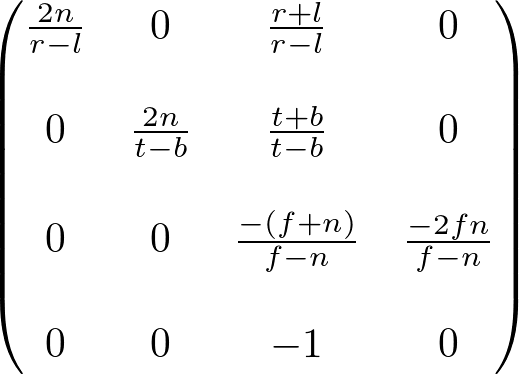
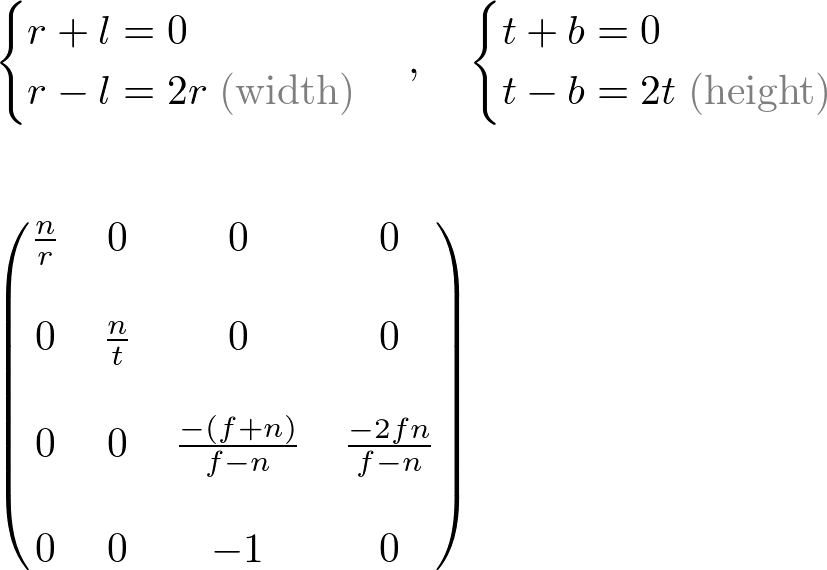



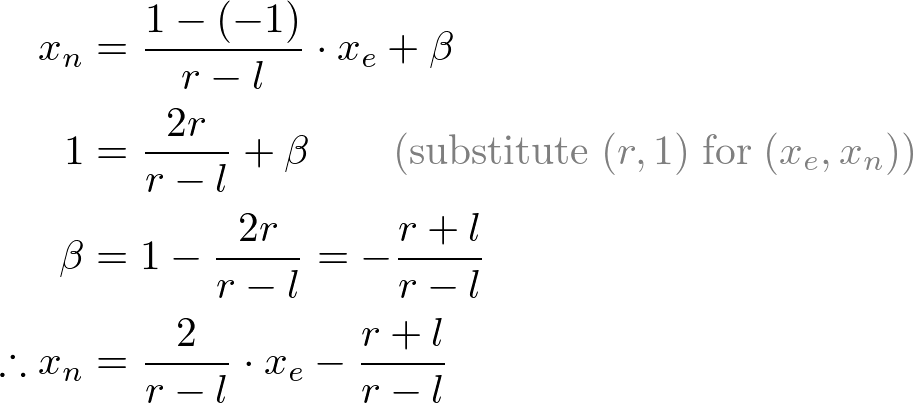

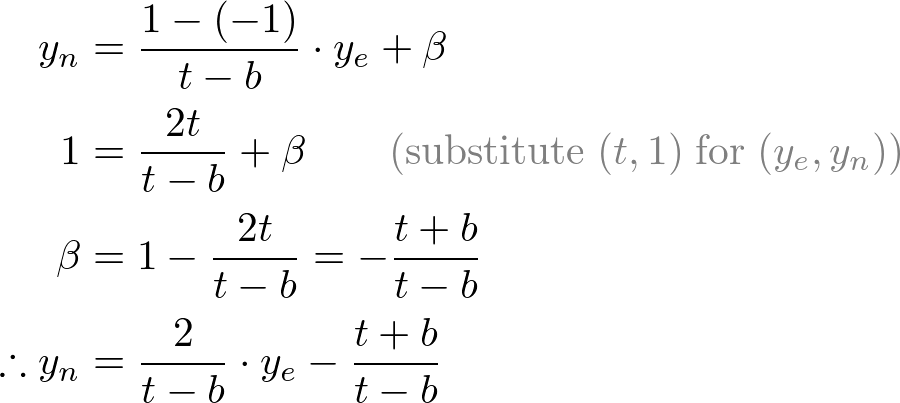

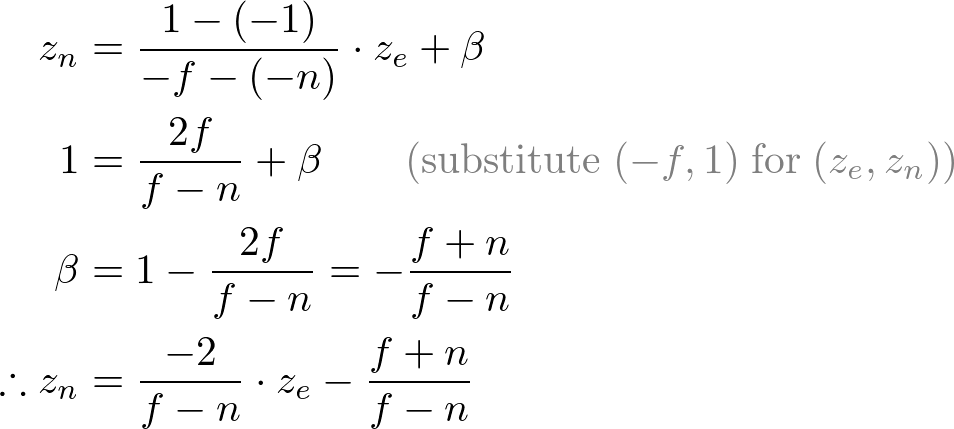
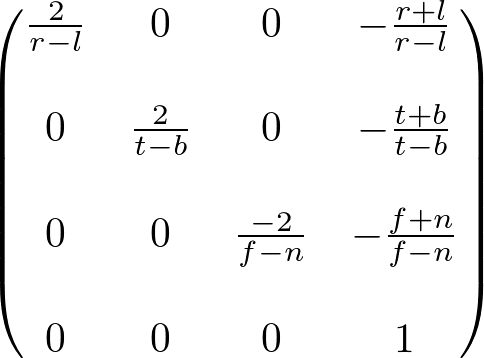
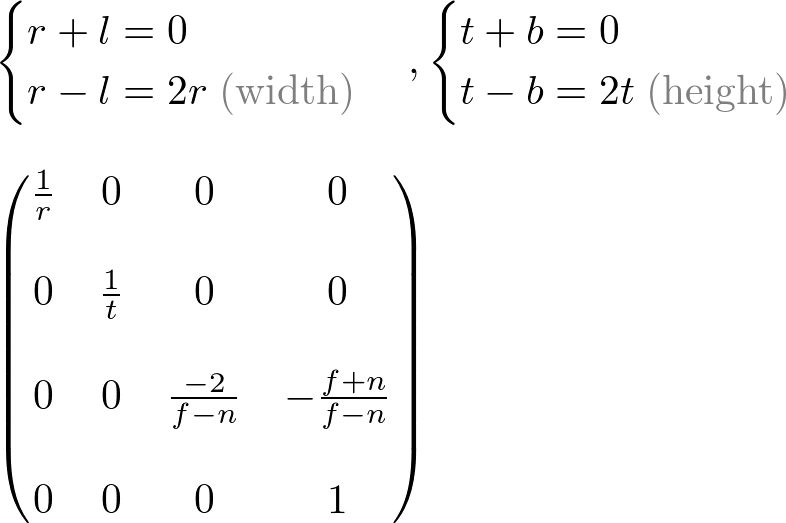



相关推荐
3. 感知矩阵(Projection Matrix):在压缩感知中,用于将信号从高维空间投影到低维空间的矩阵,其设计直接影响采样率和信号恢复质量。 4. 相干性(Mutual Coherence):感知矩阵和稀疏化矩阵之间的相关性。在压缩...
在OpenGL中,模型视图矩阵(Model-View Matrix)和投影矩阵(Projection Matrix)是两个至关重要的概念,它们用于描述物体在3D空间中的位置和形状,并将其转换到2D屏幕上的可视图像。 模型视图矩阵是将物体从其本地...
GEE错误:Error: Projection: The CRS of a map projection could not be parsed. (Error code: 3) 我正在尝试在 Albers 等积投影 ( https://code.earthengine.google.com/ccab6721def78c24dc2a0e079866a6fe ) 中...
欧拉公式求长期率的matlab代码像素投影 2d和3d投影的集合。 去做: 文件 图形支持 兼容性 它可以与PixiJS v5一起使用。 对于v4,请参见,npm版本0.2.8对于v5.1,请使用npm版本0.3.5 它甚至可以与CanvasRenderer一起...
在这个“matrixProjection.zip”压缩包中,包含的是一个使用OpenGL编程的实例,专注于解释和演示模型视图矩阵(Model-View Matrix)的概念。这个例子特别适合在Windows操作系统下运行,提供了源代码和可执行程序,...
2. **投影矩阵(Projection Matrix)**:投影矩阵决定了3D空间中的物体如何被映射到2D屏幕上。常见的投影类型有正交投影和透视投影。透视投影模拟真实世界的视觉效果,物体离摄像机越远显得越小;正交投影则使所有物体...
在计算机视觉领域,图像处理和3D重建是重要的研究方向,而其中的关键步骤之一就是对投影矩阵(Projection Matrix)的理解和应用。投影矩阵P能够描述一个三维物体如何被投影到二维图像平面上,包含了相机的内在特性...
2. **投影矩阵(Projection Matrix)**:在OpenGL中,为了将3D空间中的物体投影到2D屏幕上,我们需要使用投影矩阵。常见的有正交投影和透视投影。透视投影更符合人的视觉习惯,可以产生近大远小的效果。 3. **透视...
由OpenGL渲染的3D场景必须作为2D图像投影到计算机屏幕上。投影变换采用glu投影矩阵。首先,它将所有顶点数据从眼睛坐标转换为剪辑坐标。然后,通过与剪辑坐标的w分量相除,这些剪辑坐标也被转换为归一化设备坐标...
在本例中,我们可以使用模型视图矩阵(Model-View Matrix)来放置和旋转球体,以及投影矩阵(Projection Matrix)来控制视角和投影方式。 矩阵平移是通过在矩阵中添加或减去向量值来改变物体的位置。在OpenGL中,这...
在MATLAB中,`Affine_projection.m` 文件很可能是一个实现了投影仿射算法的脚本或函数。这个函数通常会包含以下几个关键部分: 1. **初始化参数**:首先,需要定义算法的相关参数,如目标维度(即降维后的维度)、...
此外,OpenGL ES还提供了透视投影(perspective projection)功能,将三维空间的物体映射到二维屏幕上。这涉及到更复杂的矩阵变换,如投影矩阵和视口变换,通常通过glFrustum()、glOrtho()或gluPerspective()等函数...
在OpenGL中,可以通过`glOrtho()`函数来设置平行投影矩阵。 ##### 2.1 平行投影实现 在给出的代码片段中,`reshape()`函数被用来设置视口和投影矩阵。其中,`glOrtho()`函数用于设置平行投影矩阵: ```c++ void ...
文章标题《Optimized projection matrix for compressive sensing》和描述表明本文将重点讨论压缩感知技术中测量矩阵的优化方法。在压缩感知理论中,测量矩阵的性能直接影响信号恢复的效率和准确性。文章特别强调了...
由已知对应图像点(u1, v1),(u2, v2)和投影矩阵m1, m2求相应三维点。 %the function is used to reconstruct three dimension of the points %u1,v1 is the computer image coordinate in the first image. %u2,...
本文档介绍了一种快速准确地从世界、视图与投影(World-View-Projection, WVP)矩阵中提取视锥体(Viewing Frustum)平面的方法。这种方法在游戏开发和其他三维图形应用领域非常实用,能够有效提高渲染效率,减少...
标题中的"TristanvanLeeuwen-Variable-Projection-for-FWI.zip"似乎是一个关于地震成像技术的压缩包,由Tristan van Leeuwen创建,其中包含与“变量投影法”(Variable Projection Method)在全波形反演(Full ...
这种投影可能采用了不同的方式,如正射投影(Orthographic Projection),其中点云的每个点在平面上的投影与它们在空间中的实际方向保持一致,或者透视投影(Perspective Projection),它模拟了眼睛观察物体时的...
6. **矩阵堆栈**:在旧版的OpenGL中,有模型视图矩阵(Modelview Matrix)和投影矩阵(Projection Matrix)堆栈,开发者可以直接推入和弹出矩阵进行变换操作。然而在现代OpenGL(Core Profile)中,这些堆栈已被移除...