Introduction
Entropy is a
measure
of disorder, or more precisely unpredictability. For example, a series of coin tosses with a fair coin has maximum entropy, since there is no way to predict what will come next.
A string of coin tosses with a coin with two heads and no tails has zero entropy, since the coin will always come up heads. Most collections of data in the real world lie somewhere in between. It is important to realize the difference between the entropy of
a set of possible outcomes, and the entropy of a particular outcome. A single toss of a fair coin has an entropy of one bit, but a particular result (e.g. "heads") has zero entropy, since it is entirely "predictable".
English text has fairly low entropy. In other words, it is fairly predictable. Even if we don't know exactly what is going to come next, we can be fairly certain that, for example, there will
be many more e's than z's, or that the combination 'qu' will be much more common than any other combination with a 'q' in it and the combination 'th' will be more common than any of them. Uncompressed, English text has about one
bit of entropy for each byte (eight bits) of message.[citation
needed]
If a
compression scheme is lossless—that is, you can always recover the entire original message by uncompressing—then a compressed message has the same total entropy as the original, but in fewer bits. That is, it has more entropy per bit. This means a compressed
message is more unpredictable, which is why messages are often compressed before being encrypted. Roughly speaking,
Shannon's source coding theorem says that a lossless compression scheme cannot compress messages, on average, to have more than one bit of entropy per bit of message. The entropy of a message is in a certain sense a measure of how much information it really
contains.
Shannon's theorem also implies that no lossless compression scheme can compress all messages. If some messages come out smaller, at least one must come out larger. In the real world, this
is not a problem, because we are generally only interested in compressing certain messages, for example English documents as opposed to random bytes, or digital photographs rather than noise, and don't care if our compressor makes random messages larger.
最初定义
信息理论的鼻祖之一Claude E. Shannon把信息(熵)定义为离散随机事件的出现概率。所谓信息熵,是一个数学上颇为抽象的概念,在这里不妨把信息熵理解成某种特定信息的出现概率。
对于任意一个随机变量 X,它的熵定义如下:变量的不确定性越大,熵也就越大,把它搞清楚所需要的信息量也就越大。
信息熵是信息论中用于度量信息量的一个概念。一个系统越是有序,信息熵就越低;反之,一个系统越是混乱,信息熵就越高。所以,信息熵也可以说是系统有序化程度的一个度量。
Named after
Boltzmann's H-theorem, Shannon denoted the entropy H of a
discrete random variable X with possible values {x1, ...,
xn} as,
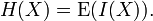
Here E is the
expected value, and I is the
information content of X.
I(X) is itself a random variable. If p denotes the
probability mass function of X then the entropy can explicitly be written as

where b is the
base of the
logarithm used. Common values of b are 2,
Euler's number e, and 10, and the unit of entropy is
bit for b=2,
nat for b=e, and
dit (or digit) for b=10.[3]
In the case of pi=0 for some i, the value of the corresponding summand 0logb0 is taken to be 0, which is consistent with the
limit:
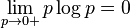 .
.
The proof of this limit can be quickly obtained applying
l'Hôpital's rule.
计算公式
H(x)=E[I(xi)]=E[ log(1/p(xi)) ]=-∑p(xi)log(p(xi)) (i=1,2,..n)
具体应用示例
1、香农指出,它的准确信息量应该是 = -(p1*log p1 + p2 * log p2 + ... +p32 *log p32),其中,p1,p2 , ...,p32 分别是这 32 个球队夺冠的概率。香农把它称为“信息熵” (Entropy),一般用符号 H 表示,单位是比特。有兴趣的读者可以推算一下当 32 个球队夺冠概率相同时,对应的信息熵等于五比特。有数学基础的读者还可以证明上面公式的值不可能大于五。
2、在很多情况下,对一些随机事件,我们并不了解其概率分布,所掌握的只是与随机事件有关的一个或几个随机变量的平均值。例如,我们只知道一个班的学生考试成绩有三个分数档:80分、90分、100分,且已知平均成绩为90分。显然在这种情况下,三种分数档的概率分布并不是唯一的。因为在下列已知条件限制下p1*80+p2*90+p3*100=90,P1+p2+p3=1。有无限多组解,该选哪一组解呢?即如何从这些相容的分布中挑选出“最佳的”、“最合理”的分布来呢?这个挑选标准就是最大信息熵原理。
按最大信息熵原理,我们从全部相容的分布中挑选这样的分布,它是在某些约束条件下(通常是给定的某些随机变量的平均值)使信息熵达到极大值的分布。这一原理是由杨乃斯提出的。这是因为信息熵取得极大值时对应的一组概率分布出现的概率占绝对优势。从理论上可以证明这一点。在我们把熵看作是计量不确定程度的最合适的标尺时,我们就基本已经认可在给定约束下选择不确定程度最大的那种分布作为随机变量的分布。因为这种随机分布是最为随机的,是主观成分最少,把不确定的东西作最大估计的分布。
3 Data as a Markov process
A common way to define entropy for text is based on the
Markov model of text. For an order-0 source (each character is selected independent of the last characters), the binary entropy is:

where pi is the probability of i. For a first-order
Markov source (one in which the probability of selecting a character is dependent only on the immediately preceding character), the
entropy rate is:

where i is a state (certain preceding characters) and
pi(j) is the probability of
j given
i as the previous character.
For a second order Markov source, the entropy rate is
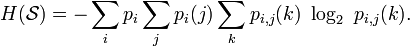 4 b-ary entropy
4 b-ary entropy
In general the b-ary entropy of a source 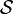 = (S,P) with
source alphabet S = {a1, ..., an} and
discrete probability distribution P = {p1, ...,
pn} where pi is the probability of ai (say
pi = p(ai)) is defined by:
= (S,P) with
source alphabet S = {a1, ..., an} and
discrete probability distribution P = {p1, ...,
pn} where pi is the probability of ai (say
pi = p(ai)) is defined by:

Note: the b in "b-ary entropy" is the number of different symbols of the "ideal alphabet" which is being used as the standard yardstick to measure source alphabets. In information theory, two symbols are
necessary and sufficient for an alphabet to be able to encode information, therefore the default is to let
b = 2 ("binary entropy"). Thus, the entropy of the source alphabet, with its given empiric probability distribution, is a number equal to the number (possibly fractional) of symbols of the "ideal alphabet", with an optimal probability distribution,
necessary to encode for each symbol of the source alphabet. Also note that "optimal probability distribution" here means a
uniform distribution: a source alphabet with n symbols has the highest possible entropy (for an alphabet with
n symbols) when the probability distribution of the alphabet is uniform. This optimal entropy turns out to be
 .
.
分享到:






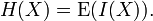

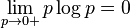 .
.

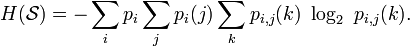
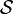 = (S,P) with
= (S,P) with

 .
.


相关推荐
信息熵理论与熵权法是决策分析和信息处理领域中的重要工具,它们在评估和量化不确定性方面发挥着关键作用。熵是热力学中的一个概念,后来被引入到信息论中,由美国数学家克劳德·香农在20世纪40年代提出。在信息技术...
在标签中,“transfer_entropy”和“transferentropy”是同义词,指的是传递熵的概念,“entropy”则是信息熵,它是传递熵的基础。"widelymfx"可能是一个特定的库或者工具箱,专为复杂系统分析提供支持,其中包括...
本文将深入探讨信息熵、序列信息熵、联合熵以及互信息等相关概念,并介绍如何通过提供的MATLAB脚本`mutInfo.m`、`jointEntropy.m`和`entropy.m`来计算这些值。 首先,我们来理解信息熵(Entropy)。信息熵是信息论...
基于信息熵的图像分割技术,该方法能快速准确找到阈值
### 信息熵与信息理论概览 #### 一、引言 信息论是一门研究信息传输、存储和处理的学科,其核心概念包括信息熵、信道容量等。本篇文章将基于Robert M. Gray教授的经典教材《Entropy and Information Theory》进行...
根据提供的文件名“互信息熵的matlab代码.docx”,我们可以推测文档中可能包含了用于计算熵和互信息的MATLAB代码示例。这些函数通常会涉及到概率分布的计算和上述公式的实现。 例如,一个简单的实现可能包括以下几...
- **香农熵公式**:香农提出了信息熵的概念,并给出了计算熵的公式:\(H(X) = -\sum_{i=1}^{n} p(x_i) \log_2 p(x_i)\),其中\(p(x_i)\)表示随机变量\(X\)取值为\(x_i\)的概率。 #### 四、信息处理的应用 - **计算...
标题“mi.rar_MATLAB 信息熵_mutual information_互信息理论_互信息理论mi_互信息的计算”表明这是一个与MATLAB相关的工具包,专注于信息熵和互信息的计算。这个压缩包可能包含了实现这两种量的计算函数和相关示例...
**信息熵(Entropy)** 信息熵通常表示为H(X),它定义了一个离散随机变量X的不确定性。熵的计算公式为: \[ H(X) = -\sum_{i=1}^{n} P(x_i) \log_2 P(x_i) \] 其中,\( P(x_i) \) 是随机变量X取第i个值的概率,n是...
图像加密等)的性能评价指标集包括:平均梯度,边缘强度,信息熵,灰度均值,标准差(均方差MSE),均方根误差,峰值信噪比(psnr),空间频率(sf),图像清晰度,互信息(mi),结构相似性(ssim),交叉熵(cross entropy)...
信息论是一门研究信息的度量、传输和处理的学科,而熵则是衡量信息量的一个重要概念。本文档名为《信息论与熵的入门介绍》,作者Tom Carter,这是一份适合初学者阅读的材料,涵盖了信息论的基础知识和熵理论的相关...
**信息熵(Entropy)**: 信息熵是衡量随机变量不确定性的一种度量,由克劳德·香农在1948年提出。对于离散随机变量X,其概率分布为P(X),信息熵H(X)定义为: \[ H(X) = -\sum_{i=1}^{n} P(x_i) \log_2 P(x_i) \] ...
2. 信息熵(Information Entropy): 信息熵是信息理论中的一个关键概念,衡量的是信息的不确定性或信息量。在图像处理中,信息熵通常用来评估图像的纹理复杂度和均匀性。一个高熵图像表示其像素分布比较均匀,含有...
b) 计算每个基因组的信息熵谱; c) 计算信息熵比谱; d) 它提取已识别的突变数量、它们的索引位置,然后保存包括光谱在内的所有数据; e) 此外,程序对两个基因组进行基点到基点比较,以通过直接比较检测突变。 ...
信息熵(Entropy)是衡量信源不确定性的度量,它表达了单位信息的平均信息量。在02-信源与信息熵.ppt中,会详细介绍熵的定义、计算方法以及其在信息压缩中的应用。 接着,**离散信道及信道容量**是通信系统中的重要...
在香农的信息熵公式中,它表示为H(X) = -∑ p(x) log2(p(x)),其中X是一个离散随机变量,p(x)是X取值x的概率,log2是以2为底的对数,通常用于计算比特(bits)的数量。熵越大,表示随机变量的不确定性越高,即包含的...
matlab代码,包含功能:计算互信息、香农熵、Renyi熵、条件熵、加权熵、加权互信息等。用法举例: >> y = [1 1 1 0 0]'; >> x = [1 0 1 1 0]'; >> mi(x,y) %% mutual information I(X;Y) >> h(x) %% entropy H(X) >>...
2. **Shannon熵**:描述的是一个离散随机变量的信息熵,是所有可能值的熵的加权平均。在Matlab中,可以通过遍历所有可能的概率分布并应用上述公式来计算Shannon熵。 3. **互信息(Mutual Information)**:衡量两个...