引自http://www.gamedev.net/reference/programming/features/2dRotatedRectCollision/
2D
Rotated Rectangle Collision
by Eric Meythaler
Introduction
While working on a project for school,
I found it necessary to perform a collision check between sprites that had been
translated and rotated. I wanted to use bounding boxes because a per-pixel
check was time consuming and unnecessary. After a couple of days of research I
managed to work out an efficient solution using the separating axis theorem.
After explaining my method to classmates and a few lab technicians, I realized
that the game development community could benefit from a clear and thorough
explanation of the process. Knowledge of linear algebra, specifically vector
math, is useful but not necessary for understanding this article.
Separating Axis Theorem
The separating axis theorem states that
for a pair of convex polygons that are not in a state of collision there exists
an axis perpendicular to an edge of one of the polygons that has no overlap
between the projected vertices of the two polygons. Essentially, what this
means is that if we project the vertices of the two polygons that we are
testing onto each axis that is perpendicular to the edges of each polygon and
we detect an overlap on each polygon there is a collision, if even one axis
shows no overlap then a collision is impossible. This solution works for any
collision possibility, even the dreaded cross collision.

Figure 1. Cross
Collision
Setting Up
Before we dive into the collision algorithm
itself, there are a few prerequisites for this particular method. Firstly,
although the separating axis theorem can be used to check for collisions
between any convex polygons, rectangles are the normal collision method in 2D,
so I will assume that you are using rectangles. Additionally, I will assume
that you can convert your rectangles into a structure with four vectors, each
representing a corner, and labeled or organized in such a way that you can tell
which corner is which (specifically, we need to be able to identify which
corners are adjacent – if the upper-left corner has been rotated until it is on
the bottom of the rectangle that’s fine, just so long as it remains connected
by an edge to the corners labeled upper-right and lower-left.).
The Method
The problem with checking for collision between two rotated
rectangles is really a matter of being able to decide when they’re not
colliding. The simple intersection test used by the Microsoft InteresectRect()
function will check if the minimum and maximum x and y values of rectangle B
are within the minimum and maximum x and y values of rectangle A. This method
works fine for axis-aligned rectangles, but when dealing with rotated
rectangles we need something a little more complex.
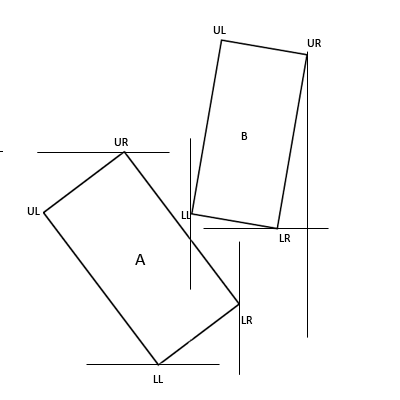
Figure 2.
Standard Bounds-based Collision Check
As you can see, the minimum x value of B lies within the
space defined by the minimum and maximum x values of A. Additionally, the
minimum y value of B lies within the space defined by the minimum and maximum y
values of A. With simple bounds based collision detection this would register
as a collision, when it clearly is not.
Step 1
The first step in this method is to determine the axes that we
will be projecting our vertices onto. The separating axis theorem states that
we must have an axis that is perpendicular to each of the edges of our two
polygons.
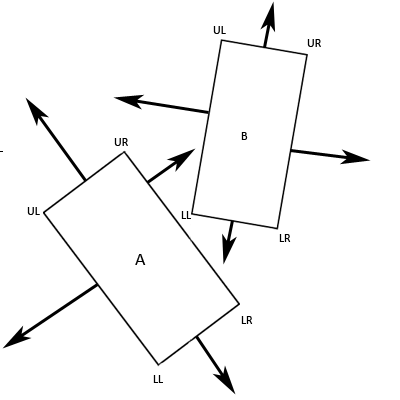
Figure 3. The
Eight Perpendicular Axes
As you can see, we end up with eight axes. You should also
immediately see the benefits of using rectangles. Firstly, each edge has an
opposite edge which shares an identical axis, we can take advantage of this to
lower the number of axes that need checked to four. Secondly, the angle that
exists between any two adjacent edges on a rectangle is 90 degrees. As such, for
any edge of a rectangle, both of the adjacent edges are perpendicular to it.
This means that we can calculate our four axes to be as such:
Axis1.x = A.UR.x - A.UL.x
Axis1.y = A.UR.y - A.UL.y
Axis2.x = A.UR.x - A.LR.x
Axis2.y = A.UR.y - A.LR.y
Axis3.x = B.UL.x - B.LL.x
Axis3.y = B.UL.y - B.LL.y
Axis4.x = B.UL.x - B.UR.x
Axis4.y = B.UL.y - B.UR.y
Meaning that Axis 1 is the resultant vector of the
upper-right corner of A minus the upper-left corner of A and so on. This gives
us four axes, each of which is perpendicular to two opposite edges of one of
the rectangles, meaning that for each edge we have an axis that is
perpendicular to it.
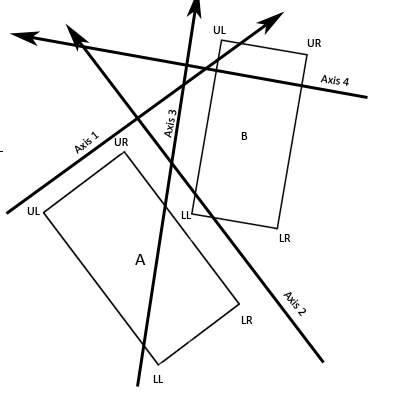
Figure 4. Our
Four Axes
Step 2
The next step is to project the vectors representing the four
corners of each rectangle onto each of the axes. If you know how to do matrix
projections then you should have no problem doing this. If you understand
vectors, but have forgotten how to do projections, then here is the equation
for the projection of rectangle A’s upper-right corner onto Axis 1:
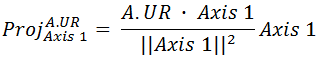
Here is the equation expanded out into scalar math and
simplified:
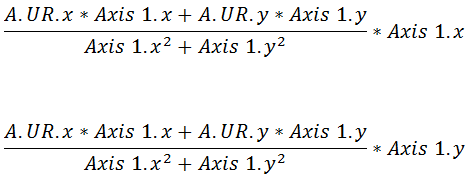
It is important to note that the only difference between
these two equations is that we’re multiplying by Axis 1’s x coordinate at the end of the first equation and
we’re multiplying by Axis 1’s y
coordinate at the end of the second equation. That will give you the x and y
coordinates of A.UR projected onto Axis 1. As an example, let’s pretend that
A.UR is at location (2, 6) and Axis 1 is represented by the vector (3, 4):
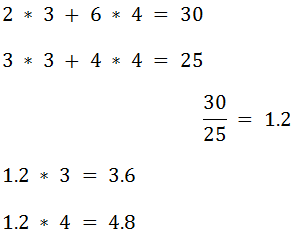
Therefore, in this example, the x coordinate of A.UR
projected onto Axis 1 is 3.6 and the y coordinate is 4.8.
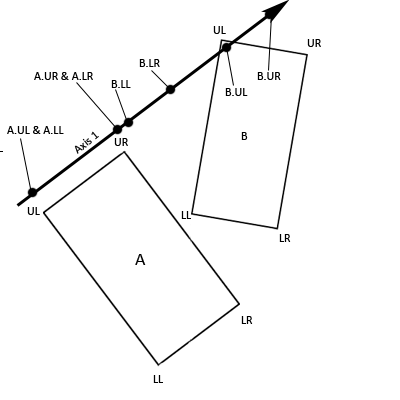
Figure 5.
Vectors Projected Onto Axis 1
Step 3
The third step in this algorithm is to calculate scalar values
that will allow us to identify the maximum and minimum projected vectors for
each of the rectangles. While it might seem natural to use the norm (length) of
the vectors, this won’t work as coordinates with negative values will return a
positive scalar value. The simplest and cheapest solution is to take the dot
product of each of the vectors and the axis. This will give us an essentially
meaningless scalar value, however, this value will be indicative of the
vector’s position on the axis. To use our above example:
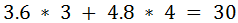
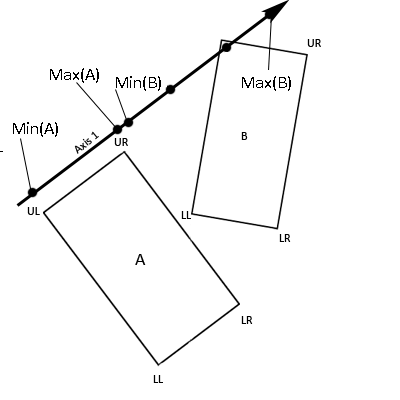
Figure 6. The
minimum and maximum scalar values
Step 4
Now identify the maximum and minimum scalar values (the ones that
we just calculated) for rectangle A and rectangle B. If the minimum scalar
value of B is less than or equal to the maximum scalar value of A and/or the
maximum scalar value of B is greater than or equal to the minimum scalar value
of A then our objects overlap when projected onto this axis.
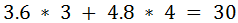

Figure 7. No
Overlap = No Collision
Repeat
Repeat steps 2, 3, and 4 for each of the axes. If all of the axes
show an overlap then there is a collision, if even one of the axes shows no
overlap then there is no collision.
Optimizations
There are a few things that can be done to optimize this
algorithm:
 You can and should
stop checking for
collision the instant you find an axis where the rectangles don’t overlap.
Remember, the separating axis theorem says that if two polygons are colliding all
axes that are perpendicular to the edges of the polygons will show an overlap
.
Meaning that, if one axis shows no overlap, then collision is not possible and
you should opt out to prevent unnecessary math.
You can and should
stop checking for
collision the instant you find an axis where the rectangles don’t overlap.
Remember, the separating axis theorem says that if two polygons are colliding all
axes that are perpendicular to the edges of the polygons will show an overlap
.
Meaning that, if one axis shows no overlap, then collision is not possible and
you should opt out to prevent unnecessary math.
 It can really pay off to transform rectangle B
into rectangle A’s local space. In order to do this, you should maintain these
rectangles in local space and then transform rectangle B into world space and
then by the inverse of rectangle A’s world space transform to put rectangle B
into rectangle A’s local space. Then, translate both rectangles equally so that
rectangle A is centered about the x and y axes. This means that two of the four
axes that you need to project vectors onto are the unit (x and y) axes. Simply
check for overlap between the x values of the corners of both rectangles and
between the y values of the corners of both rectangles. With this solution you
only have to actually project the vectors onto arbitrary axes twice, instead of
four times.
It can really pay off to transform rectangle B
into rectangle A’s local space. In order to do this, you should maintain these
rectangles in local space and then transform rectangle B into world space and
then by the inverse of rectangle A’s world space transform to put rectangle B
into rectangle A’s local space. Then, translate both rectangles equally so that
rectangle A is centered about the x and y axes. This means that two of the four
axes that you need to project vectors onto are the unit (x and y) axes. Simply
check for overlap between the x values of the corners of both rectangles and
between the y values of the corners of both rectangles. With this solution you
only have to actually project the vectors onto arbitrary axes twice, instead of
four times.
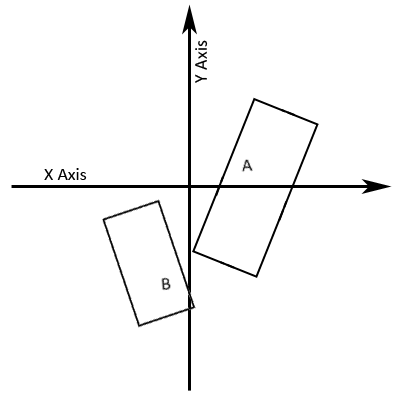
Figure 8.
Rectangles A and B in world space
Figure 9.
Rectangles A and B Transformed Into A's Local Space
 It can be wise to utilize a radius that
completely encompasses the rectangle. If the distance between the centers of
rectangles A and B is greater than the radius of A and B added together then
there cannot possibly be a collision and it is unnecessary to use the
separating axis theorem.
It can be wise to utilize a radius that
completely encompasses the rectangle. If the distance between the centers of
rectangles A and B is greater than the radius of A and B added together then
there cannot possibly be a collision and it is unnecessary to use the
separating axis theorem.
分享到:










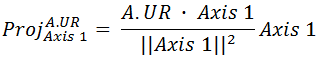
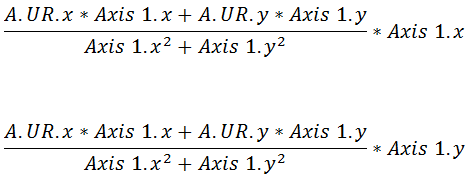
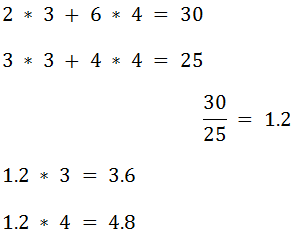

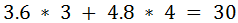






相关推荐
总结,"cocos2dx碰撞检测(支持sprite矩形旋转)"涉及的关键技术是分离轴定理,通过C++代码实现这一算法,可以有效地处理旋转精灵之间的碰撞检测。在实际的游戏开发中,这样的功能对于创建动态且真实的交互至关重要...
分离轴检测算法是一种在2D计算机图形学和游戏开发中广泛应用的碰撞检测技术。它主要用于检测多边形对象之间的碰撞,特别是在实时计算和物理模拟中。这种算法基于数学的几何原理,可以高效地判断两个2D多边形是否发生...
- 碰撞检测后,可能需要计算碰撞后的状态,如分离轴定理(Separating Axis Theorem)用于确定是否有真实的接触。 - 还可以计算碰撞点、碰撞深度以及反弹角度等信息,这对于物理模拟和游戏中的碰撞响应至关重要。 ...
4. **分离轴定理(SAT)**:对于非轴对齐的矩形(多边形),可以使用分离轴定理进行碰撞检测。该理论基于一个假设:如果两个多边形没有相交,那么存在至少一条轴,使得它们在该轴上的投影不重叠。 5. **广义交叉...
- **分离轴定理(Separating Axis Theorem, SAT)**:这是检测二维刚体碰撞的常用方法,适用于任意多边形。对于圆形与矩形,我们需要检查圆心到矩形每条边的最短距离,如果所有这些距离都大于或等于圆的半径,那么...
- **分离轴定理(Separating Axis Theorem, SAT)**:该定理指出,如果两个轴对齐的边界框在所有可能的轴上都没有重叠,那么它们就没有发生碰撞。在二维空间中,这意味着检查两个矩形的水平和垂直边是否相交。 3. ...
因此,可以采用更复杂的算法,如分离轴定理(Separating Axis Theorem, SAT),它通过找到两个矩形的所有潜在分离轴并检查它们是否重叠来确定是否存在碰撞。 在Android中,开发者通常会使用Java或Kotlin编写碰撞...
检测两者是否碰撞,可以采用不同的算法,例如分离轴定理(Separating Axis Theorem,SAT)或极值点法。 1. **分离轴定理(SAT)**: - 这是一个通用的碰撞检测方法,适用于任何两个凸形状的碰撞检测。对于圆形和...
- **分离轴定理(Separating Axis Theorem, SAT)**:这是一种通用的2D碰撞检测方法,通过检查所有可能的分离轴(矩形的边和对角线)来确定是否有重叠。 - **轴对齐边界框(Axis-Aligned Bounding Box, AABB)**:...
2. SAT(Separating Axis Theorem,分离轴定理):更高级的碰撞检测方法,适用于任意多边形。通过找到所有可能的分离轴并检查是否有重叠来判断是否发生碰撞。在处理多个矩形时,SAT可能更为高效。 四、游戏循环 ...
在三维图形学和碰撞检测领域,"分离轴定理"(Separating Axis Theorem,简称SAT)是一种广泛使用的算法,它为解决两个对象之间的潜在碰撞提供了理论基础。这个概念对于游戏开发、物理模拟以及任何需要实时碰撞检测的...
对于这种情况,可以使用更高级的碰撞检测算法,如分离轴定理(Separating Axis Theorem, SAT)。但作为基础,矩形法已经足够应对大部分简单的2D游戏需求。 在`Classes`目录中,你可能会找到游戏对象(如精灵)的C++...
- **分离轴定理(Separating Axis Theorem, SAT)**:一种更高级的碰撞检测方法,但可能超出本示例的范围。它涉及到将矩形投影到各个轴上,如果所有轴上的投影都没有重叠,那么这两个矩形就不会碰撞。 - **重叠...
- 对于更复杂的运动或旋转矩形,可能需要使用分离轴定理(Separating Axis Theorem,SAT)或旋转边界框(OBB,Obbiedient Bounding Box)检测。 4. **源码分析**: - 这个压缩包中的"4-14-4(多矩形碰撞)"可能是...
分离轴定理(Separating Axis Theorem, SAT)适用于多边形碰撞检测,它基于这样的原理:如果两个非穿透多边形存在一个轴,在该轴上它们的投影没有重叠,那么这两个多边形就没有碰撞。这个算法虽然比AABB更复杂,但能...
分离轴定理是一种用于检测两个多边形是否相交的高级方法。它通过检查多边形对所有可能的轴是否分离来判断是否发生碰撞。如果找不到任何分离轴,那么两个多边形就发生了碰撞。对于泡泡这类近似圆形的形状,可以通过...
5. **精确碰撞检测**:如果需要更精确的检测,可以使用分离轴定理(Separating Axis Theorem, SAT)。该算法可以确保没有假阳性(即看起来相交但实际上没有的碰撞)。 6. **处理碰撞**:一旦检测到碰撞,就需要采取...
对于初步筛选后可能存在碰撞的物体,需要进行精确碰撞检测,例如使用分离轴定理(Separating Axis Theorem, SAT)或GJK(Gouraud–Johnson–Keller)算法。这些方法能确定物体之间是否真正接触,并提供接触点信息。 ...
3. **碰撞检测算法**:矩形碰撞检测通常有两种常见方法:轴对齐边界框(AABB)测试和分离轴定理(SAT)。AABB测试是最简单的,只需要比较矩形的边界是否相交。SAT稍微复杂一些,它涉及到找出两个矩形的所有边,并...
综上所述,二维碰撞检测小程序涉及到的知识点包括:多边形几何、碰撞检测理论(分离轴定理、包围盒检测)、动态碰撞检测策略、以及实际编程实现中的数据结构和算法。理解并掌握这些知识点,将有助于我们创建出功能...