Dynamic Programming - Integer Knapsack

Reference: https://web.cs.ship.edu/~tbriggs/dynamic/

The Integer Knapsack problem is a famous rubrick in Computer Science. The problem has a simple brute-force solution. However, solving large instances of this problem requires considerable work (run-time).

The problem is often given as a story:

A thief breaks into a house. Around the thief are various objects: a diamond ring, a silver candelabra, a Bose Wave Radio (tm), a large portrait of Elvis Presley painted on a black velvet background (a "velvet-elvis"), and a large tiffany crystal vase. The thief has a knapsack that can only hold a certain capacity. Each of the items has a value and a size, and cannot hold all of the items in the knapsack.

Item	Size	Value
1 - ring	1	15
2 - candelabra	5	10
3 - radio	3	9
4 - elvis	4	5

 

The problem is, which items should the thief take? If the knapsack were large enough, the thief could take all of the items and run. But, that is not the case (the problem states that the knapsack cannot hold all of the items). There are three types of "thieves" that we shall consider: a greedy thief, a foolish and slow thief, and a wise thief. Each of these thieves have a knapsack that can old a total size of 8.

The greedy thief breaks into the window, and sees the items. He makes a mental list of the items available, and grabs the most expensive item first. The ring goes in first, leaving a capacity of 7, and a value of 15. Next, he grabs the candelabra, leaving a knapsack of size 2 and a value of 25. No other items will fit in his knapsack, so he leaves.

The foolish and slow thief climbs in the window, and sees the items. This thief was a programmer, downsized as part of the "dot-bomb" blowout. Possessing a solid background in boolean logic, he figures that he can simply compute all combinations of the objects and choose the best. So, he starts going through the binary combinations of objects - all 2^5 of them. While he is still drawing the truth table, the police show up, and arrest him. Although his solution would certainly have given him the best answer, it just took long to compute.

The wise thief appears, and observes the items. He notes that an empty knapsack has a value of 0. Further, he notes that a knapsack can either contain each item, or not. Further, his decision to include an item will be based on a quick calculation - either the knapsack with some combination of the previous items will be worth more, or else the knapsack of a size that will fit the current item was worth more. So, he does this quick computation, and figures out that the best knapsack he can take is made up of items 1,3, and 4, for a total value of 29.

 

Greedy Algorithms

The mistake the first thief made was that he was too greedy. He took the items in non-decreasing order by their value. He ended up with a knapsack that was not completely filled. Not having a knapsack filled completely does not necessarily imply that the solution will be bad, but it is often the case.

One advantage to this technique is that it can be done very quickly. The amount of work for this solution is relative to how many objects the thief has to look at. In the worst case, how many items would this be? How much work is involved?

The greedy algorithm does not work for this version of the problem; but there is another closely related version. Suppose that instead of objects, there were piles of dust. The first pile was platinum dust, the second pile was gold, and the third pile were silver dust. In this version of the problem, the thief will fill his sack with as much as the sack will hold. If there were still capacity, the thief will next fill the sack with gold, and finally, silver. This version of the problem is often called the "Continuous Knapsack" problem.

Q: What key difference is there in the continuous problem that makes a greedy solution work?

 

Brute Force

The mistake the second thief in our rubric made was to try to enumerate all of the possible choices. There are 2⁵ combinations in this example. Expressed more generally, there are 2ⁿ combinations of items that the thief can choose. This can be expressed as the power set of the items. Algorithms that require enumeration of this set will require exponential work: O(2ⁿ). Clearly, as the size of the set increases, the amount of work will increase exponentially.

 

Dynamic Programming

The wise thief used a technique that is known as "dynamic programming." In this case, a table was made to track "the best knapsack so far." The complete table that is show in subsequent examples is for demonstration purposes. In the following example, there is a column that indicates a range of values from 0 to the 9. This corresponds to the "target weight" of the knapsack. The table stops at the maximum capacity of the knapsack. There are then n+1 columns, one each for the items that can be selected.

The first column is initialized to zero. Logically, this corresponds to a knapsack with zero items having zero worth. The first row is also initialized to zero, corresponding to a knapsack of zero capacity.

Finally, the values of the table are filled in, from left to right, and from top to bottom. For each cell item, the total worth of a knapsack is determined as either the worth of a knapsack without the current item (expressed as the value directly to the left of the current value), or it is the value of the knapsack with the current item added into it.

Items> Capacity		i:1 15/1	i:2 10/5	i:3 9/3	i:4 5/4
0	0^	0^	0^	0^	0^
1	0^	15^	15^	15^	15^
2	0^	15^	15^	15^	15^
3	0^	15^	15^	15<	15^
4	0^	15^	15^	24^	24<
5	0^	15^	15<	24^	24<
6	0^	15^	25^	25<	25<
7	0^	15^	25^	25<	25<
8	0^	15^	25^	25<	29^

 

Observe in the previous example, the knapsack starts at zero, and the computation continues down the first column. Since the first item has a size of one, a knapsack of value 15 can be made for all of the columns. The next column shows that knapsacks less than size 5 can only be made using an empty knapsack or else using only the first item. For knapsacks over size six, then a decision must be made: is it better to build a knapsack with both items, or only with one of them.

What makes this different than the greedy algorithm happens when processing the third item. First, notice that the best knapsack that can be made, up until size four, does not include the third item. Then, when the capacity of the knapsack increases enough to hold the third item, the value changes - the value of the knapsack now includes the second and third items, for a total value of 25. Finally, when the capacity is large enough to hold all three items, then the capacity is grown to hold all three items. However, following the same pattern for the fourth item, it is apparent that algorithm works by showing that including the fourth item in place of any other item is not required.

A More Concise Definition

Let S={s₁,s₂,..s_n} be a set of weights, and V={v₁,v₂,..v_n}. Let t be a target capacity, representing the largest total weight the knapsack can hold. A solution to the knapsack problem is:

 

 and 

The solution will be the one with the maximum value, ,and the minimum weight. The group {0,1} serves to indicate that the item is either in the knapsack, or it is not.

Recurrence Relation

One approach to solving this problem is to break the problem down in terms of its sub-problems. Consider trying to build a knapsack of size W. The question to answer is, should item i be included in the knapsack or not. Including item i should make a knapsack of higher value than all previous knapsacks of size W. But, if the knapsack is already at size W, including item i will make the knapsack too large. So, the solution has to examine a knapsack of size W-wi. Specifically, consider a knapsack of size W-wi that does not include item i. To decide if the item should be included in the knapsack, compare the values of the knapsack of size W that does not include the current item; and the value of a knapsack of size W-wi + the value of item i. If the worth of the knapsack is increased by taking including the item, that item i will be included in the knapsack, and its overall value will be increased. So, a recurrence relation can be developed:

Solving this recursive version of the knapsack problem will return the correct answer, but will be very inefficient. Note that it will repeatedly solve the same set of sub-problems, generating a series of recursive calls that will grow as the recursive Fibonacci sequence did.

 

Memoization

The dynamic programming version of this problem is essentially a memoization approach to solving this problem. Instead of repeatedly solving the same sub-problems, create a table that contains the results of previous evaluations of the sub-problems, and using that to increase the speed of the solution. The table must contain k rows (the target capacity), and i columns (the number of items). Ignoring boundary conditions, each cell of the table can be computed using the following function:

max( T[i-1,j], vi + T[i-1, j-wi] )

It is this memoization approach that leads to the final pseudo-code solution to the problem:

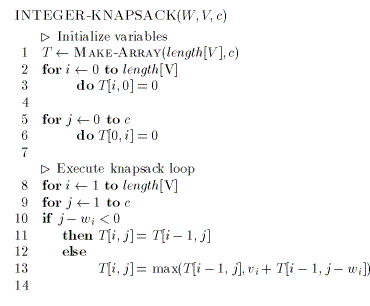
This pseudo-code is extremely similar to the previous recurrence relation. The major difference is that this algorithm starts at the smallest knapsack and grows to fill the final table. The recurrence relation starts at the largest solution and solves to the smallest.

Run-Time Analysis

The run-time of this knapsack will depend on the size of the table. Its two factors were k rows (determined by the target capacity), and the n columns (the number of items in the set. So, the run-time of this version will be θ(k*n). Caution should be observed here: k is not a constant, and its size may be considerably larger than the number of items in the set. This is a type of algorithm that exhibits pseudo-polynomial time.

pseudo-polynomial time

def. An algorithm whose runtime is bound not only on the size of the input (e.g. n items), but also on the magnitude of the inputs of the problem.

One approach to "fixing" this problem is the Approximate Knapsack Problem.

Why Study the Knapsack Problem?

Since most people are not thieves, the knapsack problem may not seem to of much practical import. The knapsack-problem was used as the basis for acryptographic system (that has since been broken). However, the problem arises in several constraint satisfacation problems (CSP). Consider any problem where the solution depends on selecting some number of items whose values are maximized (or minimized), and whoose weight is equal to a target value.

Java Source Code

public int integerKnapsack(int[] weights, int[] values, int capacity) {
	int[][] d = new int[weights.length+1][capacity+1];
	for(int i=1; i<=weights.length; i++) {
		for(int j=1; j<=capacity; j++) {
			if(weights[i-1] > j) {
				d[i][j] = d[i-1][j];
			} else {
				d[i][j] = Math.max(d[i-1][j], d[i-1][j-weights[i-1]]+values[i-1]);
			}
		}
	}
	return d[weights.length][capacity];
}

public void testIntegerKnapsack() {
	int[] weights = {1,5,3,4};
	int[] values = {15,10,9,5};
	int capacity = 8;
	int maxValue = integerKnapsack(weights, values, capacity);
	System.out.println(maxValue);
}

Reference:

https://web.cs.ship.edu/~tbriggs/dynamic/