- 浏览: 979102 次
- 性别:

- 来自: 珠海
-

文章分类
最新评论
-
Yunjey:
Yunjey 写道这样子的话、grid中的editable如何 ...
Flex创建可编辑以及分页的DataGrid -
Yunjey:
这样子的话、grid中的editable如何设置啊?!
Flex创建可编辑以及分页的DataGrid -
di1984HIT:
写的很好~~
JCalendar组件 -
sanny81:
此文真棒!感谢一路风尘的奉献!
但我有一疑 ...
Filter发送自定义数据详解 -
umgsai:
求完整demo umgsai@126.com
Flex和Jsp创建用户登入系统
前一篇文章没有系统地介绍这个模型,本篇文章将详细介绍
1. 定义:
The Hidden Markov Model is a finite set of states , each of which is associated with a (generally multidimensional) probability distribution []. Transitions among the states are governed by a set of probabilities called transition probabilities. In a particular state an outcome or observation can be generated, according to the associated probability distribution. It is only the outcome, not the state visible to an external observer and therefore states are ``hidden'' to the outside; hence the name Hidden Markov Model.
隐马尔科夫模型是由有限个状态组成的,每一个状态都以一定的概率出现,状态之间的转换由转换概率表决定,每一个状态都可以产生一个观察到的状态,在隐马尔科夫模型中,只有观察到的状态所见,真实的马尔科夫状态链不可见,因此被称为隐马尔科夫模型,该模型包含如下三个要素:
- The number of states of the model, N .
- The number of observation symbols in the alphabet, M . If the observations are continuous then M is infinite.
- A set of state transition probabilities
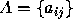 .
.
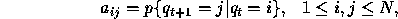
where
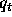 denotes the current state.
denotes the current state.
Transition probabilities should satisfy the normal stochastic constraints,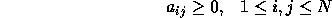
and
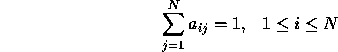
- A probability distribution in each of the
states,
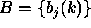 .
.
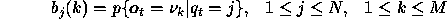
where
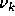 denotes the
denotes the 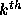 observation symbol in the
alphabet, and
observation symbol in the
alphabet, and 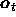 the current parameter vector.
the current parameter vector.
Following stochastic constraints must be satisfied.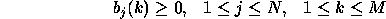
and
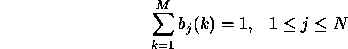
If the observations are continuous then we will have to use a continuous probability density function, instead of a set of discrete probabilities. In this case we specify the parameters of the probability density function. Usually the probability density is approximated by a weighted sum of M Gaussian distributions
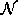 ,
,
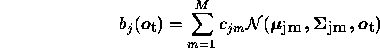
where,
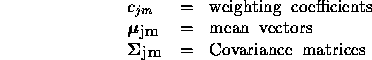
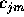 should satisfy the stochastic constrains,
should satisfy the stochastic constrains,
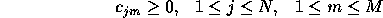
and
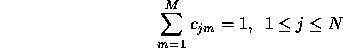
- The initial state distribution,
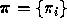 .
.
where,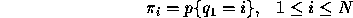
Therefore we can use the compact notation
![]()
to denote an HMM with discrete probability distributions, while
![]()
to denote one with continuous densities. .
所以,一个隐马尔科夫模型可记为
![]()
2.一些假设:
For the sake of mathematical and computational tractability, following assumptions are made in the theory of HMMs.
![]()
In other words it is assumed that
the next state is dependent only upon the current state. This is
called the Markov assumption and the resulting model becomes
actually a first order HMM.
However generally the next state may depend on past k
states and
it is possible to obtain a such model, called an ![]() order HMM by defining
the transition probabilities as follows.
order HMM by defining
the transition probabilities as follows.
![]()
But it is seen that a higher order HMM will have a higher complexity. Even though the first order HMMs are the most common, some attempts have been made to use the higher order HMMs too.
![]()
for
any ![]() and
and ![]() .
.
![]()
.
Then according to the assumption for an HMM ![]() ,
,
![]()
However unlike the other two, this assumption has a very limited validity. In some cases this assumption may not be fair enough and therefore becomes a severe weakness of the HMMs.
3.要解决的三个问题:
Once we have an HMM, there are three problems of interest.
Evaluation problem can be used for isolated (word) recognition. Decoding problem is related to the continuous recognition as well as to the segmentation. Learning problem must be solved, if we want to train an HMM for the subsequent use of recognition tasks.
4. 估计观察序列的概率问题:
We have a model ![]() and a sequence of observations
and a sequence of observations
![]() , and
, and ![]() must be found. We can calculate this quantity using
simple probabilistic arguments. But this calculation involves number of
operations in the order of
must be found. We can calculate this quantity using
simple probabilistic arguments. But this calculation involves number of
operations in the order of ![]() . This is very large even if the
length of the sequence, T
is moderate. Therefore we have to look
for an other method for this calculation. Fortunately there exists
one which has a considerably low complexity and makes use an
auxiliary variable,
. This is very large even if the
length of the sequence, T
is moderate. Therefore we have to look
for an other method for this calculation. Fortunately there exists
one which has a considerably low complexity and makes use an
auxiliary variable, ![]() called forward variable
.
called forward variable
.
The forward variable is defined as the probability of the partial
observation sequence ![]() , when it terminates at the
state i
. Mathematically,
, when it terminates at the
state i
. Mathematically,
前向变量:观察到O1,O2,..,Ot并且t时刻Qt = i 的概率,它是按t向前推进的,当t=T时,整个观察序列都已经获取到,因此只要对所有的前向变量在T时刻的值求和就得到了观察序列出现的概率
Then it is easy to see that following recursive relationship holds.
where,
![]()
Using this recursion we can calculate
![]()
and then the required probability is given by,
The complexity of this method, known as the forward algorithm
is proportional to ![]() , which is
linear wrt T
whereas the direct calculation mentioned earlier, had an
exponential complexity.
, which is
linear wrt T
whereas the direct calculation mentioned earlier, had an
exponential complexity.
In a similar way we can define the backward variable
![]() as the probability of the partial observation sequence
as the probability of the partial observation sequence
![]() , given that the current state is
i
. Mathematically ,
, given that the current state is
i
. Mathematically ,
后向变量定义的时t时刻之后产生的某一个观察序列的概率,而前向变量定义的是这个时刻之前的观察序列的概率,根据前面三个假设中的最后一个,因此整个序列的概率等于前向 与后向的乘积
As in the case of ![]() there is a recursive relationship
which can be used to calculate
there is a recursive relationship
which can be used to calculate ![]() efficiently.
efficiently.
where,
![]()
Further we can see that,
Therefore this gives another way to calculate ![]() , by using both forward and backward variables as given
in eqn. 1.7
.
, by using both forward and backward variables as given
in eqn. 1.7
.
Eqn. 1.7 is very useful, specially in deriving the formulas required for gradient based training.
5.解码问题:
In this case We want to find the most likely state sequence for a
given sequence of observations, ![]() and a model,
and a model, ![]()
The solution to this problem depends upon the way ``most likely state
sequence'' is defined. One approach is to find the most likely state
![]() at t
=t
and to concatenate all such '
at t
=t
and to concatenate all such ' ![]() 's. But some times
this method does not give a physically meaningful state sequence.
Therefore we would go for another method which has no such problems.
's. But some times
this method does not give a physically meaningful state sequence.
Therefore we would go for another method which has no such problems.
In this method, commonly known as Viterbi algorithm
, the whole
state sequence with the maximum likelihood is found. In order to
facilitate the computation we define an auxiliary variable,
![]()
which gives the highest probability that partial observation sequence and state sequence up to t =t can have, when the current state is i .
上面的公式定义:在t时刻,结束状态是i,并且观察到的序列是O1...t-1的最大概率,因此解码问题就变成求在T时刻,概率最大的结束状态
It is easy to observe that the following recursive relationship holds.
where,
![]()
这个递推公式说明如下:
由前面的第三个假设可知,t时刻转换到t + 1 时刻,这个概率与已经发生的观察序列无关,因此我们只需要保存在每个状态上的最大概率,然后在计算这个状态进行到下一个状态的概率,将二者进行乘积即得到在t + 1时刻该路径的概率,然后在N个值中选择一个最大的值
So the procedure to find the most likely state sequence starts from
calculation of ![]() using recursion in 1.8
, while always keeping a pointer to the
``winning state'' in the maximum finding operation. Finally
the state
using recursion in 1.8
, while always keeping a pointer to the
``winning state'' in the maximum finding operation. Finally
the state ![]() , is found where
, is found where
![]()
and starting from this state, the sequence of states
is back-tracked as the pointer in each state indicates.This gives the
required set of states.
This whole algorithm can be interpreted as a search in a graph whose
nodes are formed by the states of the HMM in each of the time instant
![]() .
.
From :http://blog.csdn.net/tianqio/archive/2009/06/17/4275895.aspx (THX)
发表评论
-
值得收藏的23个搜索下载免费PDF电子书的网站
2010-04-03 08:36 2891我们常常需要寻找一些电子书PDF 文件,特别是一些国外的英文版 ... -
小技巧:保存word中图片的最另类最简单办法
2010-03-25 21:34 4891时常,我们会把图片加入到word中,但是将word文件与其他人 ... -
最小二乘法
2010-02-25 11:28 1641一个不错的例子,对初学的人有帮助! 一个在线的演示例子(jav ... -
信号强度从百分比到分贝的转换
2009-11-21 23:50 18496Radio Frequency(RF)信号强度 ... -
IPod Shuttle(1G)充电问题
2009-11-17 10:58 2018最近总是发现我的IPod充电的时候,灯总是黄色一闪一闪 ... -
不再繁琐!Word 2007实现自动编排目录
2009-09-09 10:58 4023最近不少学生朋友在忙� ... -
网络数据库
2009-08-18 11:41 1542警示: 合理使用电子资源,保 ... -
单位冲激函数(图)
2009-08-17 17:36 8053上一回说到,单个矩形脉冲的时域波形如下图: 图1 ... -
介绍两款在线数学公式编辑器
2009-08-16 12:51 11864当然了,在线的不能像Math Type那样,可以随心所欲的编 ... -
Autoregressive Models
2009-08-12 22:27 1333The autoregressive model is one ... -
重要性抽样方法
2009-07-31 11:10 3060考虑积分: 设 ε1 是 [0 , ... -
卡尔曼滤波简介及其算法实现代码
2009-07-29 17:49 25817卡尔曼滤波算法实现代� ... -
隐马尔科夫模型HMM自学(2)
2009-07-24 10:42 3918再次感谢崔晓源。 ... -
隐马尔科夫模型HMM自学(1)
2009-07-24 10:38 7721介绍 崔晓源 翻译 ... -
OPNET 14.5.A.PL1下载
2009-07-17 22:42 7513下载FTP地址 : ftp://bupt:bupt@forum ... -
Autoregressive (AR) Models
2009-07-17 20:18 1871The autoregressive (AR) mode ... -
Rao-Blackwellised粒子滤波器(RBPF)
2009-07-14 22:31 49451. Rao-Blackwellisation is a ge ... -
LZ78算法
2009-07-14 17:47 1928在介绍LZ78算法之前,首先说明在算法中用到的几个术语和符号: ... -
模式定理
2009-03-31 15:44 1530本文最初由 SpriteLW 发表于 http://bl ...


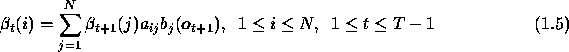



相关推荐
隐马尔可夫模型(Hidden Markov Model,HMM)是一种统计模型,被广泛应用于模式识别、自然语言处理等领域。HMM的核心思想是通过一个可以观察的马尔可夫过程来描述一个隐含的状态序列,其中状态不可直接观察到,但每...
在本主题中,我们将深入探讨基于隐马尔可夫模型(HMM)的孤立字语音识别方法,并结合MATLAB程序实现进行讲解。 隐马尔可夫模型(Hidden Markov Model, HMM)是概率统计模型,广泛应用于自然语言处理、生物信息学...
隐马尔可夫模型(Hidden Markov Model,HMM)是一种广泛应用于模式识别和序列分析的统计模型。自从1870年俄国有机化学家Vladimir V. Markovnikov提出马尔科夫模型以来,该模型在理论研究与实际应用领域都发挥了巨大...
隐马尔可夫模型及其在自然语言处理中的应用
隐马尔可夫模型(Hidden Markov Model, HMM)是一种统计建模方法,常用于处理序列数据,如语音识别、自然语言处理、生物信息学等领域。在MATLAB环境中实现HMM,我们可以利用其强大的矩阵运算能力和丰富的工具箱。...
隐马尔可夫模型(Hidden Markov Model,简称HMM)是概率统计领域中的一个重要模型,尤其在自然语言处理、语音识别、生物信息学等领域有着广泛的应用。在MATLAB环境中,我们可以利用其强大的数学计算能力和丰富的函数...
本文提出了一种基于隐马尔可夫模型的人脸识别方法,该方法利用人脸隐马尔可夫模型的结构特征和Viterbi算法的特点,对特征观察序列进行分割,并使用部分序列对所有隐马尔可夫模型递进地计算最大相似度,同时排除...
### 隐马尔可夫模型详解 #### 一、隐马尔可夫模型概述 隐马尔可夫模型(Hidden Markov Model, HMM)作为一种重要的概率图模型,在序列预测问题中扮演着核心角色。它能够有效地处理一系列数据点间的关系,并且尤其...
2.内容:基于隐马尔可夫模型回归HMMR模型的时间序列分割处理matlab仿真+代码仿真操作视频 3.用处:用于隐马尔可夫模型回归HMMR模型的时间序列分割处理算法编程学习 4.指向人群:本硕博等教研学习使用 5.运行注意...
### 连续型隐马尔可夫模型(HMM)参数迭代算法 #### 知识点解析 **一、隐马尔可夫模型(HMM)基础** 隐马尔可夫模型是一种统计模型,用于描述一个含有未知参数的马尔可夫过程。这种模型在自然语言处理、语音识别...
隐马尔可夫模型(Hidden Markov Model,简称HMM)是概率统计领域的一种重要模型,广泛应用于自然语言处理、语音识别、生物信息学等多个IT领域。本模型的核心思想是,尽管我们无法直接观测到系统的真实状态,但可以...
"隐马尔可夫模型(HMM)简介" 隐马尔可夫模型(Hidden Markov Model,HMM)是一种数学模型,用来描述一个系统的隐状态和观察状态之间的关系。在本文中,我们通过一个实例来了解 HMM 的基本概念和应用。 什么是 HMM?...
此ppt由专业人员编写,内容条例清晰,重点突出,结合了简单易懂的实例,深入浅出的介绍了隐马尔可夫模型。
隐马尔可夫模型(HMM)是一种统计建模方法,尤其在自然语言处理和语音识别领域中广泛应用。它基于马尔可夫模型的概念,但增加了“隐藏”或不可观测的状态,这些状态通过一系列可观察的输出来表现。在HMM中,系统处于...
### 隐马尔可夫模型在多序列比对中的应用 #### 1. 引言 随着现代生物学研究的进步,尤其是基因组测序技术的发展,科学家们面临着海量的生物序列数据。这些数据包括但不限于DNA序列、RNA序列及蛋白质序列等。如何...