зїІзї≠жРЬ糥
дЄЇдЇЖзїІзї≠жРЬ糥пЉМжИСдїђзЃАеНХзЪДдїОеЉАжФЊеИЧи°®дЄ≠йАЙжЛ©еЕЈжЬЙжЬАе∞ПFеАЉзЪДжЦєж†ЉпЉМзДґеРОеѓєйАЙдЄ≠зЪДжЦєж†ЉињЫи°Ме¶ВдЄЛжУНдљЬпЉЪ
4.
е∞ЖеЕґдїОеЉАжФЊеИЧи°®дЄ≠зІїйЩ§пЉМеєґеК†еИ∞е∞БйЧ≠еИЧи°®дЄ≠гАВ
5.
ж£Ай™МжЙАжЬЙзЪДзЫЄйВїжЦєж†ЉпЉМењљзХ•йВ£дЇЫдЄНеПѓйАЪињЗзЪДжИЦиАЕеЈ≤зїПеЬ®е∞БйЧ≠еИЧи°®йЗМзЪДжЦєж†ЉгАВе¶ВжЮЬињЩдЄ™зЫЄйВїжЦєж†ЉдЄНеЬ®еЉАжФЊеИЧи°®дЄ≠пЉМе∞±жККеЃГжЈїеК†ињЫеОїгАВеєґе∞ЖељУеЙНйАЙеЃЪжЦєж†ЉиЃЊдЄЇжЦ∞жЈїжЦєж†ЉзЪДзИґжЦєж†ЉгАВ
6.
е¶ВжЮЬжЯРдЄ™зЫЄйВїжЦєж†ЉеЈ≤зїПеЬ®еЉАжФЊеИЧи°®дЄ≠дЇЖпЉИжДПеС≥зЭАеЈ≤зїПжОҐжµЛињЗпЉМиАМдЄФеЈ≤зїПиЃЊзљЃињЗзИґжЦєж†ЉвАХвАХиѓСиАЕпЉЙпЉМе∞±зЬЛзЬЛжЬЙж≤°жЬЙеИ∞иЊЊйВ£дЄ™жЦєж†ЉзЪДжЫіе•љзЪДиЈѓеЊДгАВдєЯе∞±жШѓиѓіпЉМе¶ВжЮЬдїОељУеЙНйАЙдЄ≠жЦєж†ЉеИ∞йВ£дЄ™жЦєж†ЉпЉМдЉЪдЄНдЉЪдљњйВ£дЄ™жЦєж†ЉзЪДGеАЉжЫіе∞ПгАВе¶ВжЮЬдЄНиГљпЉМе∞±дЄНињЫи°МдїїдљХжУНдљЬгАВ
зЫЄеПНзЪДпЉМе¶ВжЮЬжЦ∞иЈѓеЊДзЪДGеАЉжЫіе∞ПпЉМе∞±е∞Жиѓ•зЫЄйВїжЦєж†ЉзЪДзИґжЦєж†ЉйЗНиЃЊдЄЇељУеЙНйАЙдЄ≠жЦєж†ЉгАВпЉИеЬ®дЄКеЫЊдЄ≠жШѓжФєеПШеЕґжМЗйТИзЪДжЦєеРСдЄЇжМЗеРСйАЙдЄ≠жЦєж†ЉгАВжЬАеРОпЉМйЗНжЦ∞иЃ°зЃЧйВ£дЄ™зЫЄйВїжЦєж†ЉзЪДFеТМGеАЉгАВе¶ВжЮЬдљ†зЬЛз≥КжґВдЇЖпЉМдЄЛйЭҐдЉЪжЬЙеЫЊиІ£иѓіжШОгАВ
е•љеХ¶пЉМеТ±дїђжЭ•зЬЛзЬЛеЕЈдљУзВєзЪДдЊЛе≠РгАВеЬ®еИЭеІЛжЧґзЪД9дЄ™жЦєеЭЧдЄ≠пЉМељУеЉАеІЛжֺ憊襀еК†еИ∞е∞БйЧ≠еИЧи°®еРОпЉМеЉАжФЊеИЧи°®йЗМињШеЙ©8дЄ™жЦєж†ЉгАВеЬ®ињЩеЕЂдЄ™жЦєж†ЉељУдЄ≠пЉМдљНдЇОиµЈзВєжЦєж†ЉеП≥иЊєзЪДйВ£дЄ™жЦєж†ЉеЕЈжЬЙжЬАе∞ПзЪДFеАЉ40гАВжЙАдї•жИСдїђйАЙжЛ©ињЩдЄ™жЦєж†ЉдљЬдЄЇдЄЛдЄАдЄ™дЄ≠ењГжЦєж†ЉгАВдЄЛеЫЊдЄ≠еЃГдї•йЂШдЇЃзЪДиУЭиЙ≤и°®з§ЇгАВ
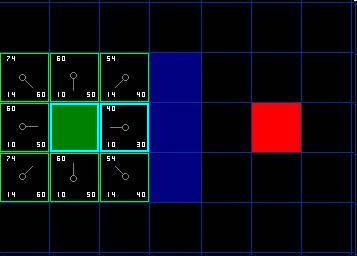
[еЫЊеЫЫ]
гАА
й¶ЦеЕИпЉМжИСдїђе∞ЖйАЙдЄ≠зЪДжЦєж†ЉдїОеЉАжФЊеИЧи°®дЄ≠зІїйЩ§пЉМеєґеК†еЕ•еИ∞е∞БйЧ≠еИЧи°®дЄ≠пЉИжЙАдї•зФ®дЇЃиУЭиЙ≤ж†ЗиЃ∞пЉЙгАВзДґеРОеЖНж£Ай™МеЃГзЪДзЫЄйВїиКВзВєгАВйВ£дєИеЬ®еЃГзіІйВїзЪДеП≥иЊєзЪДжЦєж†ЉйГљжШѓеҐЩпЉМжЙАдї•дЄНзЃ°еЃГдїђгАВеЈ¶иЊєжМ®зЭАзЪДжШѓиµЈеІЛжЦєж†ЉпЉМиАМиµЈеІЛжЦєж†ЉеЈ≤зїПеЬ®е∞БйЧ≠еИЧи°®дЄ≠дЇЖпЉМжЙАдї•жИСдїђдєЯдЄНзЃ°еЃГгАВ
еЕґдїЦеЫЫдЄ™жЦєж†ЉеЈ≤зїПеЬ®еЉАжФЊеИЧи°®дЄ≠пЉМйВ£дєИжИСдїђе∞±и¶Бж£Ай™МдЄАдЄЛе¶ВжЮЬиЈѓеЊДзїПзФ±ељУеЙНйАЙдЄ≠жЦєж†ЉеИ∞йВ£дЇЫжЦєж†ЉзЪДиѓЭдЉЪдЄНдЉЪжЫіе•љпЉМељУзДґпЉМжШѓзФ®GеАЉдљЬдЄЇеПВиАГгАВжЭ•зЬЛзЬЛйАЙдЄ≠жЦєж†ЉеП≥дЄКиІТзЪДйВ£дЄАдЄ™жЦєж†ЉпЉМеЃГељУеЙНзЪДGеАЉжШѓ14пЉМе¶ВжЮЬжИСдїђзїПзФ±ељУеЙНиКВзВєеЖНеИ∞иЊЊйВ£дЄ™жЦєж†ЉзЪДиѓЭпЉМGеАЉдЉЪжШѓ20пЉИеИ∞ељУеЙНжЦєж†ЉзЪДGеАЉжШѓ10пЉМзДґеРОеРСдЄКзІїеК®дЄАж†Ље∞±еЖНеК†дЄК10пЉЙгАВдЄЇ20зЪДGеАЉжѓФ14е§ІпЉМеЫ†ж≠§ињЩж†ЈзЪДиЈѓеЊДдЄНдЉЪжЫіе•љгАВдљ†зЬЛзЬЛеЫЊе∞±дЉЪеЃєжШУзРЖиІ£дЇЫгАВжШЊзДґдїОиµЈеІЛзВєж≤њжЦЬиІТжЦєеРСзІїеК®еИ∞йВ£дЄ™жЦєж†ЉжѓФеЕИж∞іеє≥зІїеК®дЄАж†ЉеЖНеЮВзЫізІїеК®дЄАж†ЉжЫізЫіжО•гАВ
ељУжИСдїђжМЙе¶ВдЄКињЗз®ЛдЊЭжђ°ж£Ай™МеЉАжФЊеИЧи°®дЄ≠зЪДжЙАжЬЙеЫЫдЄ™жЦєж†ЉеРОпЉМдЉЪеПСзО∞зїПзФ±ељУеЙНжЦєж†ЉзЪДиѓЭдЄНдЉЪ嚥жИРжЫіе•љзЪДиЈѓеЊДпЉМйВ£жИСдїђе∞±дњЭжМБзЫЃеЙНзЪДзКґеЖµдЄНеПШгАВзО∞еЬ®жИСдїђеЈ≤зїПе§ДзРЖдЇЖжЙАжЬЙзЫЄйВїжЦєж†ЉпЉМеЗЖе§ЗеИ∞дЄЛдЄАдЄ™жЦєж†ЉеРІгАВ
жИСдїђеЖНйБНеОЖдЄАдЄЛеЉАжФЊеИЧи°®пЉМзЫЃеЙНеП™жЬЙ7дЄ™жЦєж†ЉдЇЖгАВжИСдїђжМСдЄ™FеАЉжЬАе∞ПзЪДеРІгАВжЬЙиґ£зЪДжШѓпЉМзЫЃеЙНињЩзІНжГЕеЖµдЄЛпЉМжЬЙдЄ§дЄ™FеАЉдЄЇ54зЪДжЦєж†ЉгАВйВ£жИСдїђжАОдєИйАЙжЛ©еСҐпЉЯеЕґеЃЮйАЙеУ™дЄ™йГљж≤°еЕ≥з≥їпЉМи¶БиАГиЩСеИ∞йАЯеЇ¶зЪДиѓЭпЉМйАЙдљ†жЬАињСеК†еИ∞еЉАжФЊеИЧи°®дЄ≠зЪДйВ£дЄАдЄ™дЉЪжЫіењЂдЇЫгАВељУз¶їзЫЃзЪДеЬ∞иґКжЭ•иґКињСзЪДжЧґеАЩиґКеБПеРСдЇОйАЙжЬАеРОеПСзО∞зЪДжЦєж†ЉгАВеЃЮйЩЕдЄКињЩдЄ™зЬЯзЪДж≤°еЕ≥з≥їпЉИеѓєеЊЕињЩдЄ™зЪДдЄНеРМйА†жИРдЇЖдЄ§дЄ™зЙИжЬђзЪДA*зЃЧж≥ХеЊЧеИ∞з≠ЙйХњзЪДдЄНеРМиЈѓеЊДпЉЙгАВ
йВ£жИСдїђйАЙдЄЛйЭҐзЪДйВ£дЄ™е•љдЇЖпЉМе∞±жШѓиµЈеІЛжЦєж†ЉеП≥иЊєзЪДпЉМдЄЛеЫЊжЙАз§ЇзЪДйВ£дЄ™гАВ
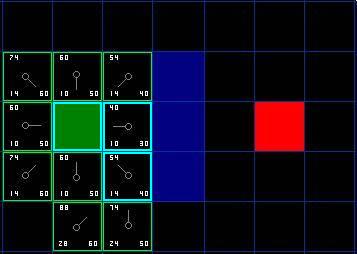
[еЫЊдЇФ]
гАА
ињЩдЄАжђ°пЉМеЬ®жИСдїђж£Ай™МзЫЄйВїжЦєж†ЉзЪДжЧґеАЩеПСзО∞еП≥иЊєзіІжМ®зЪДйВ£дЄ™жШѓеҐЩпЉМе∞±дЄНзЃ°еЃГдЇЖгАВдЄКйЭҐжМ®зЭАзЪДйВ£дЄ™дєЯеРМж†ЈењљзХ•гАВињШжЬЙеП≥иЊєеҐЩдЄЛйЭҐйВ£дЄ™жЦєж†ЉжИСдїђдєЯдЄНзЃ°гАВдЄЇдїАдєИеСҐпЉЯеЫ†дЄЇдљ†дЄНеПѓиГљеИЗз©њеҐЩиІТзЫіжО•еИ∞иЊЊйВ£дЄ™ж†Ље≠РгАВеЃЮйЩЕдЄКдљ†еЊЧеЕИеРСдЄЛиµ∞зДґеРОеЖНйАЪињЗйВ£дЄ™жЦєж†ЉгАВињЩдЄ™ињЗз®ЛдЄ≠жШѓзїХзЭАеҐЩиІТиµ∞гАВпЉИж≥®жДПпЉЪз©њињЗеҐЩиІТзЪДињЩдЄ™иІДеИЩжШѓеПѓйАЙзЪДпЉМеПЦеЖ≥дЇОдљ†зЪДиКВзВєжШѓе¶ВдљХжФЊзљЃзЪДгАВпЉЙ
йВ£дєИињШеЙ©дЄЛеЕґдїЦдЇФдЄ™зЫЄйВїжЦєж†ЉгАВељУеЙНжЦєж†ЉзЪДдЄЛйЭҐйВ£дЄ§дЄ™ињШдЄНеЬ®еЉАжФЊеИЧи°®дЄ≠пЉМйВ£жИСдїђжККеЃГдїђеК†ињЫеОїеєґдЄФжККељУеЙНжЦєж†ЉдљЬдЄЇеЃГдїђзЪДзИґжЦєж†ЉгАВеЕґдїЦдЄЙдЄ™дЄ≠жЬЙдЄ§дЄ™еЈ≤зїПеЬ®е∞БйЧ≠еИЧи°®дЄ≠дЇЖпЉИдЄ§дЄ™еЈ≤зїПеЬ®еЫЊдЄ≠зФ®дЇЃиУЭиЙ≤ж†ЗиЃ∞дЇЖпЉМиµЈеІЛжЦєж†ЉпЉМдЄКйЭҐзЪДжЦєж†ЉпЉЙпЉМжЙАдї•е∞±дЄНзФ®зЃ°дЇЖгАВжЬАеРОйВ£дЄ™пЉМељУеЙНжЦєж†ЉеЈ¶иЊєжМ®зЭАзЪДпЉМи¶Бж£АжЯ•дЄАдЄЛзїПзФ±ељУеЙНиКВзВєеИ∞йВ£йЗМдЉЪдЄНдЉЪйЩНдљОеЃГзЪДGеАЉгАВзїУжЮЬдЄНи°МпЉМжЙАдї•жИСдїђеПИе§ДзРЖеЃМжѓХдЇЖпЉМзДґеРОеОїж£Ай™МеЉАжФЊеИЧи°®дЄ≠зЪДдЄЛдЄАдЄ™ж†Ље≠РгАВ
йЗНе§НињЩдЄ™ињЗз®ЛзЫіеИ∞жИСдїђжККзЫЃзЪДжЦєж†ЉеК†еЕ•еИ∞еЉАжФЊеИЧи°®дЄ≠дЇЖпЉМйВ£жЧґеАЩзЬЛиµЈжЭ•дЉЪеГПдЄЛеЫЊињЩдЄ™ж†Је≠РгАВ
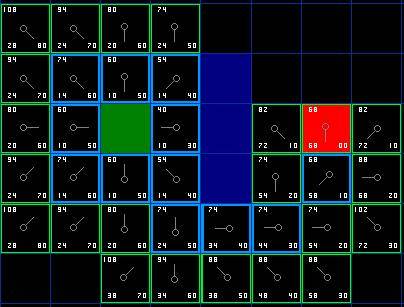
[еЫЊеЕ≠]
гАА
ж≥®жДПеИ∞ж≤°пЉЯиµЈеІЛжЦєж†ЉдЄЛдЄ§ж†ЉзЪДдљНзљЃпЉМйВ£йЗМзЪДж†Ље≠РеЈ≤зїПеТМеЙНдЄАеЉ†еЫЊдЄНдЄАж†ЈдЇЖгАВдєЛеЙНеЃГзЪДGеАЉжШѓ28еєґдЄФжМЗеРСеП≥дЄКжЦєзЪДйВ£дЄ™жЦєж†ЉгАВзО∞еЬ®еЃГзЪДGеАЉеПШжИРдЇЖ20еєґдЄФжМЗеРСдЇЖж≠£дЄКжЦєзЪДжЦєж†ЉгАВињЩдЄ™жФєеПШжШѓеЬ®жРЬ糥ињЗз®ЛдЄ≠пЉМеЃГзЪДGеАЉиҐЂж†ЄжЯ•жЧґеПСзО∞еЬ®жЯРдЄ™жЦ∞иЈѓеЊДдЄЛеПѓдї•еПШеЊЧжЫіе∞ПжЧґеПСзФЯзЪДгАВзДґеРОеЃГзЪДзИґжЦєж†ЉдєЯ襀йЗНиЃЊеєґдЄФйЗНжЦ∞иЃ°зЃЧдЇЖGеАЉеТМFеАЉгАВеЬ®жЬђдЊЛдЄ≠ињЩдЄ™жФєеПШзЬЛиµЈжЭ•е•љеГПдЄНжШѓеЊИйЗНи¶БпЉМдљЖжШѓеЬ®еЊИе§ЪзІНжГЕеЖµдЄЛињЩзІНжФєеПШдЉЪдљњеИ∞иЊЊзЫЃж†ЗзЪДжЬАдљ≥иЈѓеЊДеПШеЊЧйЭЮеЄЄдЄНеРМгАВ
йВ£дєИжИСдїђжАОж†ЈжЭ•иЗ™еК®еЊЧеЗЇеЃЮйЩЕиЈѓеЊДзЪДеСҐ?еЊИзЃАеНХпЉМеП™и¶БдїОзЇҐиЙ≤зЫЃж†ЗжЦєж†ЉеЉАеІЛж≤њзЭАжѓПдЄАдЄ™жЦєж†ЉзЪДжМЗйТИжЦєеРСзІїеК®пЉМдЊЭжђ°еИ∞иЊЊеЃГдїђзЪДзИґжЦєж†ЉпЉМжЬАзїИиВѓеЃЪдЉЪеИ∞иЊЊиµЈеІЛжЦєж†ЉгАВйВ£е∞±жШѓдљ†зЪДиЈѓеЊДпЉБе¶ВдЄЛеЫЊжЙАз§ЇгАВдїОAжЦєж†ЉеИ∞BжЦєж†ЉзЪДзІїеК®е∞±еЈЃдЄНе§ЪжШѓж≤њзЭАињЩдЄ™иЈѓеЊДдїОжѓПдЄ™жЦєж†ЉдЄ≠ењГпЉИиКВзВєпЉЙзІїеК®еИ∞еП¶дЄАдЄ™жЦєж†ЉдЄ≠ењГпЉМзЫіеИ∞жКµиЊЊзїИзВєгАВзЃАеНХеРІпЉБ
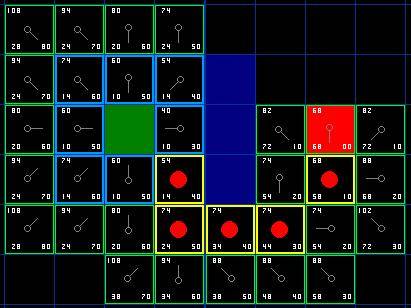
[еЫЊдЄГ]
гАА
A*зЃЧж≥ХжАїзїУ
1.
е∞ЖеЉАеІЛиКВзВєжФЊеЕ•еЉАжФЊеИЧи°®(еЉАеІЛиКВзВєзЪДFеТМGеАЉйГљиІЖдЄЇ0);
2.
йЗНе§НдЄАдЄЛж≠•й™§:
            i.
еЬ®еЉАжФЊеИЧи°®дЄ≠жЯ•жЙЊеЕЈжЬЙжЬАе∞ПFеАЉзЪДиКВзВє,еєґжККжЯ•жЙЊеИ∞зЪДиКВзВєдљЬдЄЇељУеЙНиКВзВє;
           ii.
жККељУеЙНиКВзВєдїОеЉАжФЊеИЧи°®еИ†йЩ§, еК†еЕ•еИ∞е∞БйЧ≠еИЧи°®;
         iii.
еѓєељУеЙНиКВзВєзЫЄйВїзЪДжѓПдЄАдЄ™иКВзВєдЊЭжђ°жЙІи°Мдї•дЄЛж≠•й™§:
1.
е¶ВжЮЬиѓ•зЫЄйВїиКВзВєдЄНеПѓйАЪи°МжИЦиАЕиѓ•зЫЄйВїиКВзВєеЈ≤зїПеЬ®е∞БйЧ≠еИЧи°®дЄ≠,еИЩдїАдєИжУНдљЬдєЯдЄНжЙІи°М,зїІзї≠ж£Ай™МдЄЛдЄАдЄ™иКВзВє;
2.
е¶ВжЮЬиѓ•зЫЄйВїиКВзВєдЄНеЬ®еЉАжФЊеИЧи°®дЄ≠,еИЩе∞Жиѓ•иКВзВєжЈїеК†еИ∞еЉАжФЊеИЧи°®дЄ≠, еєґе∞Жиѓ•зЫЄйВїиКВзВєзЪДзИґиКВзВєиЃЊдЄЇељУеЙНиКВзВє,еРМжЧґдњЭе≠Шиѓ•зЫЄйВїиКВзВєзЪДGеТМFеАЉ;
3.
е¶ВжЮЬиѓ•зЫЄйВїиКВзВєеЬ®еЉАжФЊеИЧи°®дЄ≠, еИЩеИ§жЦ≠иЛ•зїПзФ±ељУеЙНиКВзВєеИ∞иЊЊиѓ•зЫЄйВїиКВзВєзЪДGеАЉжШѓеР¶е∞ПдЇОеОЯжЭ•дњЭе≠ШзЪДGеАЉ,иЛ•е∞ПдЇО,еИЩе∞Жиѓ•зЫЄйВїиКВзВєзЪДзИґиКВзВєиЃЊдЄЇељУеЙНиКВзВє,еєґйЗНжЦ∞иЃЊзљЃиѓ•зЫЄйВїиКВзВєзЪДGеТМFеАЉ.
        iv.
еЊ™зОѓзїУжЭЯжЭ°дїґ:
ељУзїИзВєиКВзº襀еК†еЕ•еИ∞еЉАжФЊеИЧи°®дљЬдЄЇеЊЕж£Ай™МиКВзВєжЧґ, и°®з§ЇиЈѓеЊД襀жЙЊеИ∞,ж≠§жЧґеЇФзїИж≠ҐеЊ™зОѓ;
жИЦиАЕељУеЉАжФЊеИЧи°®дЄЇз©Ї,и°®жШОеЈ≤жЧ†еПѓдї•жЈїеК†зЪДжЦ∞иКВзВє,иАМеЈ≤ж£Ай™МзЪДиКВзВєдЄ≠ж≤°жЬЙзїИзВєиКВзВєеИЩжДПеС≥зЭАиЈѓеЊДжЧ†ж≥Х襀жЙЊеИ∞,ж≠§жЧґдєЯзїУжЭЯеЊ™зОѓ;
3.
дїОзїИзВєиКВзВєеЉАеІЛж≤њзИґиКВзВєйБНеОЖ, еєґдњЭе≠ШжХідЄ™йБНеОЖеИ∞зЪДиКВзВєеЭРж†З,йБНеОЖжЙАеЊЧзЪДиКВзВєе∞±жШѓжЬАеРОеЊЧеИ∞зЪДиЈѓеЊД;
еИЖдЇЂеИ∞пЉЪ















зЫЄеЕ≥жО®иНР
A*еѓїиЈѓзЃЧж≥Х(A* Pathfinding Algorithm)жШѓжЄЄжИПеЉАеПСгАБеЬ∞еЫЊеѓЉиИ™гАБеی嚥е§ДзРЖз≠ЙйҐЖеЯЯдЄ≠еєњж≥ЫдљњзФ®зЪДдЄАзІНйЂШжХИиЈѓеЊДжРЬ糥зЃЧж≥ХгАВеЃГзЪДж†ЄењГжАЭжГ≥жШѓеЬ®еЃљеЇ¶дЉШеЕИжРЬ糥(BFS)еТМDijkstraзЃЧж≥ХзЪДеЯЇз°АдЄКпЉМйАЪињЗеЉХеЕ•еРѓеПСеЉПеЗљжХ∞жЭ•дЉШеМЦжРЬ糥жХИзОЗпЉМе∞љ...
жЬђжХЩз®Ле∞Жиѓ¶зїЖдїЛзїНе¶ВдљХеЬ®Unity5.4.4зЙИжЬђдЄ≠еЃЮзО∞A*еѓїиЈѓзЃЧж≥ХпЉМеєґжПРдЊЫдЄАдЄ™еЃМжХізЪДDemoз§ЇдЊЛгАВ й¶ЦеЕИпЉМA*зЃЧж≥ХзЪДж†ЄењГеЬ®дЇОиѓДдЉ∞жѓПдЄ™иКВзВєзЪДFеАЉпЉМиѓ•еАЉзФ±GеАЉпЉИдїОиµЈеІЛиКВзВєеИ∞ељУеЙНиКВзВєзЪДеЃЮйЩЕжИРжЬђпЉЙеТМHеАЉпЉИдїОељУеЙНиКВзВєеИ∞зЫЃж†ЗиКВзВєзЪДйҐДиЃ°...
еЬ®жПРдЊЫзЪДеОЛзЉ©еМЕжЦЗдїґ"seekroad"дЄ≠пЉМеПѓиГљеМЕеРЂдЇЖдЄАз≥їеИЧеЕ≥дЇОA*еѓїиЈѓзЃЧж≥ХзЪДеЃЮдЊЛдї£з†БгАБжХЩз®ЛжЦЗж°£жИЦиАЕжЉФз§Їз®ЛеЇПпЉМеЄЃеК©е≠¶дє†иАЕжЫіе•љеЬ∞зРЖиІ£еТМеЇФзФ®ињЩдЄ™зЃЧж≥ХгАВйАЪињЗжЈ±еЕ•е≠¶дє†еТМеЃЮиЈµпЉМдљ†е∞ЖиГље§ЯзЖЯзїГињРзФ®A*иІ£еЖ≥еЃЮйЩЕйЧЃйҐШпЉМжПРеНЗдљ†зЪДзЉЦз®ЛиГљеКЫ...
ињЩдЄ™жХЩз®ЛвАЬиЫЃзЙЫжХЩиВ≤ зљСдЄКUnity 3D жХЩз®Л AжШЯеѓїиЈѓзЃЧж≥ХвАЭжЧ®еЬ®еЄЃеК©еЉАеПСиАЕжЈ±еЕ•зРЖиІ£еТМеЇФзФ®A*зЃЧж≥ХпЉМдї•дЊњеЬ®жЄЄжИПдЄ≠еЃЮзО∞йЂШжХИгАБжЩЇиГљзЪДиЈѓеЊДеѓїжЙЊгАВ A* еѓїиЈѓзЃЧж≥ХжШѓдЄАзІНеЯЇдЇОеЫЊзЪДжЬАзЯ≠иЈѓеЊДжРЬ糥зЃЧж≥ХпЉМеЃГзїУеРИдЇЖDijkstraзЃЧж≥ХзЪДеЕ®е±АжЬАдЉШ...
AжШЯ(A*)жРЬ糥зЃЧж≥ХжШѓдЄАзІНеєњж≥ЫеЇФзФ®еЬ®еی嚥жРЬ糥гАБжЄЄжИПеЉАеПСгАБиЈѓеЊДиІДеИТз≠ЙйҐЖеЯЯзЪДйЂШжХИеѓїиЈѓзЃЧж≥ХгАВеЃГжШѓDijkstraзЃЧж≥ХзЪДдЄАзІНжЙ©е±ХпЉМеЉХеЕ•дЇЖеРѓеПСеЉПдњ°жБѓжЭ•жПРйЂШжРЬ糥жХИзОЗпЉМеРМжЧґдњЭиѓБжЙЊеИ∞зЪДиЈѓеЊДжШѓжЬАдЉШзЪДгАВжЬђжХЩз®Ле∞ЖжЈ±еЕ•иЃ≤иІ£A*зЃЧж≥ХзЪДж†ЄењГ...
A* Pathfinding Project жШѓдЄАдЄ™еКЯиГљеЉЇе§ІеєґдЄФжШУдЇОдљњзФ®зЪД Unity еѓїиЈѓз≥їзїЯгАВйАЪињЗењЂйАЯзЪДиЈѓеЊДеѓїжЙЊпЉМжВ®зЪД AI е∞ЖзЂЛеН≥еЬ®е§НжЭВзЪДињЈеЃЂдЄ≠жЙЊеИ∞зО©еЃґгАВйЭЮеЄЄйАВеРИ TDгАБFPSгАБRTS жЄЄжИПгАВ жФѓжМБеѓЉиИ™зљСж†ЉпЉМжФѓжМБ3DгАБ2DеѓїиЈѓгАВ
гАКRPGжЄЄжИП45еЇ¶иІЖиІТеЬ∞еЫЊдЄОA*еѓїиЈѓзЃЧж≥Хиѓ¶иІ£гАЛ еЬ®иЃ°зЃЧжЬЇжЄЄжИПеЉАеПСйҐЖеЯЯпЉМе∞§еЕґжШѓиІТиЙ≤жЙЃжЉФжЄЄжИПпЉИRole-Playing GameпЉМзЃАзІ∞RPGпЉЙдЄ≠пЉМ45еЇ¶иІТеЬ∞еЫЊжЄ≤жЯУеТМеѓїиЈѓзЃЧж≥ХжШѓдЄ§дЄ™иЗ≥еЕ≥йЗНи¶БзЪДжКАжЬѓгАВжЬђиµДжЇРвАЬRGPжЄЄжИПдЇЇзЙ©45еЇ¶еЬ∞еЫЊ+AжШЯеѓїиЈѓзЃЧж≥Х...
A*пЉИиѓїдљЬ"A-star"пЉЙзЃЧж≥ХжШѓдЄАзІНеєњж≥ЫеЇФзФ®зЪДеѓїиЈѓзЃЧж≥ХпЉМеЫ†еЕґйЂШжХИжАІеТМеЗЖз°ЃжАІиАМе§ЗеПЧйЭТзЭРгАВеЬ®UnityеЉХжУОдЄ≠пЉМжЬЙдЄУйЧ®зЪДжПТдїґжФѓжМБA*еѓїиЈѓпЉМе¶В"A Pathfinding Project Pro"пЉМеЕґзЙИжЬђдЄЇ4.1.16пЉМдЄЇжИСдїђжПРдЊЫдЇЖеЉЇе§ІзЪДеѓїиЈѓеКЯиГљгАВ A*зЃЧж≥Х...
A*еѓїиЈѓзЃЧж≥ХжШѓжЄЄжИПеЉАеПСеТМиЈѓеЊДиІДеИТйҐЖеЯЯдЄ≠еєњж≥ЫеЇФзФ®зЪДдЄАзІНйЂШжХИжРЬ糥зЃЧж≥ХпЉМе∞§еЕґеЬ®UnityеЉХжУОдЄ≠пЉМеЃГ襀府ж≥ЫзФ®дЇОеИЫеїЇжЩЇиГљиІТиЙ≤зЪДеѓЉиИ™з≥їзїЯгАВA*зЃЧж≥ХзїУеРИдЇЖDijkstraзЃЧж≥ХзЪДеЕ®йЭҐжАІеТМжЬАдљ≥дЉШеЕИжРЬ糥зЪДжХИзОЗпЉМйАЪињЗеЉХеЕ•еРѓеПСеЉПдњ°жБѓжЭ•жМЗеѓЉ...
AжШЯпЉИA*пЉЙзЃЧж≥ХжШѓдЄАзІНеЬ®еی嚥жРЬ糥дЄ≠еєњж≥ЫдљњзФ®зЪДиЈѓеЊДиІДеИТзЃЧж≥ХпЉМзЙєеИЂжШѓеЬ®жЄЄжИПеЉАеПСдЄ≠зФ®дЇОеЃЮзО∞иІТиЙ≤жИЦзЙ©дљУзЪДиЗ™еК®еѓїиЈѓеКЯиГљгАВеЃГзїУеРИдЇЖжЬАдљ≥дЉШеЕИжРЬ糥пЉИBFSпЉЙзЪДеЕ®е±АжЬАдЉШжАІеТМDijkstraзЃЧж≥ХзЪДжХИзОЗпЉМйАЪињЗеЉХеЕ•еРѓеПСеЉПеЗљжХ∞жЭ•дЉ∞иЃ°дїОиµЈзВєеИ∞...
A*иЗ™еК®еѓїиЈѓзЃЧж≥ХжШѓдЄАзІНеєњж≥ЫеЇФзФ®еЬ®жЄЄжИПеЉАеПСгАБеЬ∞еЫЊеѓЉиИ™з≠ЙйҐЖеЯЯдЄ≠зЪДйЂШжХИиЈѓеЊДжРЬ糥зЃЧж≥ХгАВеЃГзїУеРИдЇЖDijkstraзЃЧж≥ХзЪДжЬАзЯ≠иЈѓеЊДзЙєжАІдЄОBFSпЉИеєњеЇ¶дЉШеЕИжРЬ糥пЉЙзЪДжХИзОЗпЉМйАЪињЗиѓДдЉ∞еЗљжХ∞жЭ•жМЗеѓЉжРЬ糥пЉМдї•жЙЊеИ∞дїОиµЈзВєеИ∞зїИзВєзЪДжЬАдЉШиЈѓеЊДгАВеЬ®зїЩеЃЪ...
жЬђиµДжЇР"20210812-AжШЯеѓїиЈѓзЃЧж≥Х.rar"еМЕеРЂдЇЖдЄАжђ°жЈ±еЕ•зЪДдЇМеПЙж†СдЄОA*зЃЧж≥ХзЪДеЃЮиЈµжХЩз®ЛпЉМзїУеРИиІЖйҐСжХЩе≠¶гАБжЇРдї£з†БеТМзђФиЃ∞пЉМжЧ®еЬ®еЄЃеК©е≠¶дє†иАЕжЈ±еЕ•зРЖиІ£еєґжОМжП°ињЩдЄ§зІНеЕ≥йФЃжКАжЬѓгАВ дЄАгАБдЇМеПЙж†СеЯЇз°АзЯ•иѓЖ дЇМеПЙж†СжШѓзФ±nдЄ™иКВзВєзїДжИРзЪДжХ∞жНЃзїУжЮД...
еЬ®жШУиѓ≠и®АдЄ≠еЃЮзО∞AжШЯеѓїиЈѓзЃЧж≥ХпЉМжШѓдЄЇдЇЖиІ£еЖ≥жЄЄжИПгАБеЬ∞еЫЊеѓЉиИ™з≠ЙйҐЖеЯЯдЄ≠зЪДиЈѓеЊДиІДеИТйЧЃйҐШгАВAжШЯпЉИA*пЉЙзЃЧж≥ХжШѓдЄАзІНйЂШжХИзЪДеРѓеПСеЉПжРЬ糥зЃЧж≥ХпЉМеЃГзїУеРИдЇЖDijkstraзЃЧж≥ХеТМжЬАдљ≥дЉШеЕИжРЬ糥пЉМиГље§ЯжЙЊеИ∞дїОиµЈзВєеИ∞зїИзВєзЪДжЬАзЯ≠иЈѓеЊДгАВ AжШЯзЃЧж≥ХзЪДж†ЄењГ...
жЬђжХЩз®Ле∞ЖжЈ±еЕ•жОҐиЃ®C++еЃЮзО∞зЪДеѓїиЈѓзЃЧж≥ХпЉМињЩеѓєдЇОжЄЄжИПеЉАеПСиАЕжЭ•иѓіжШѓењЕе§ЗзЪДеЯЇз°АзЯ•иѓЖгАВ й¶ЦеЕИпЉМжИСдїђи¶БдЇЖиІ£еѓїиЈѓзЃЧж≥ХзЪДеЯЇжЬђж¶ВењµгАВеѓїиЈѓзЃЧж≥ХжШѓдЄАзІНзФ®дЇОиІ£еЖ≥зљСзїЬдЄ≠иКВзВєйЧіжЬАзЯ≠иЈѓеЊДйЧЃйҐШзЪДжЦєж≥ХпЉМе¶ВDijkstraзЃЧж≥ХгАБA*зЃЧж≥Хз≠ЙгАВеЬ®жЄЄжИП...
еОЛзЉ©еМЕдЄ≠зЪД`AжШЯ.e`еПѓиГљжШѓAжШЯзЃЧж≥ХзЪДеЯЇжЬђеЃЮзО∞жЦЗдїґпЉМ`AжШЯдЄЙзїізЃЧж≥Х.e`еПѓиГљжЙ©е±ХеИ∞дЇЖдЄЙзїіз©ЇйЧізЪДеЇФзФ®пЉМиАМ`AжШЯеѓїиЈѓ`еПѓиГљжШѓзЫЄеЕ≥иЊЕеК©жЦЗдїґжИЦжµЛиѓХзФ®дЊЛгАВеЬ®EжШУиѓ≠и®АдЄ≠пЉМдљ†йЬАи¶БзРЖиІ£ињЩдЇЫжЇРз†БжЦЗдїґдЄ≠зЪДжХ∞жНЃзїУжЮДгАБеЗљжХ∞и∞ГзФ®еТМйАїиЊСжµБз®ЛпЉМ...
ж†ЗйҐШдЄ≠зЪДвАЬUnityдЄЛA*зЃЧж≥ХеЃЮзО∞вАЭжМЗзЪДжШѓеЬ®UnityжЄЄжИПеЉХжУОдЄ≠дљњзФ®A*еѓїиЈѓзЃЧж≥ХжЭ•иІ£еЖ≥жЄЄжИПдЄ≠зЪДиЈѓеЊДиІДеИТйЧЃйҐШгАВA*зЃЧж≥ХжШѓдЄАзІНеРѓеПСеЉПжРЬ糥зЃЧж≥ХпЉМеєњж≥ЫеЇФзФ®дЇОжЄЄжИПеЉАеПСгАБеЬ∞еЫЊеѓЉиИ™з≠ЙйҐЖеЯЯпЉМеЃГйАЪињЗиѓДдЉ∞иКВзВєзЪДдї£дїЈдЉ∞иЃ°жЭ•жЩЇиГљеЬ∞йАЙжЛ©иЈѓеЊДпЉМ...
зїЉдЄКжЙАињ∞пЉМAжШЯеѓїиЈѓзЃЧж≥ХеЬ®UnityдЄ≠зЪДеЃЮзО∞дЄНдїЕжґЙеПКеИ∞зЃЧж≥ХеОЯзРЖпЉМињШеМЕжЛђдЇЖдЄОUnityеЉХжУОзЪДжХіеРИгАБйЪЬзҐНзЙ©е§ДзРЖгАБеРѓеПСеЉПеЗљжХ∞зЪДйАЙжЛ©дї•еПКжАІиГљдЉШеМЦз≠Йе§ЪдЄ™жЦєйЭҐгАВйАЪињЗињЩдЄ™й°єзЫЃпЉМеЉАеПСиАЕеПѓдї•жЮДеїЇеЗЇе§НжЭВиАМйЂШжХИзЪДеѓїиЈѓз≥їзїЯпЉМдЄЇжЄЄжИПдЄ≠зЪДAI...
AжШЯ(A*)зЃЧж≥ХжШѓдЄАзІНеЬ®еی嚥жРЬ糥дЄ≠йЭЮеЄЄжЬЙжХИзЪДиЈѓеЊДжЯ•жЙЊзЃЧж≥ХпЉМе∞§еЕґйАВзФ®дЇОжЄЄжИПеЉАеПСдЄ≠зЪДиЗ™еК®еѓїиЈѓз≥їзїЯгАВVBпЉИVisual BasicпЉЙжШѓдЄАзІНзФ±еЊЃиљѓеЕђеПЄжО®еЗЇзЪДдЇЛдїґй©±еК®зЉЦз®Лиѓ≠и®АпЉМеЃГдї•еЕґжШУе≠¶жАІеТМзЫіиІВжАІеПЧеИ∞иЃЄе§Ъз®ЛеЇПеСШзЪДеЦЬзИ±гАВе∞ЖAжШЯзЃЧж≥ХдЄО...
A*пЉИA-starпЉЙзЃЧж≥ХжШѓдЄАзІНзФ®дЇОиЈѓеЊДжЯ•жЙЊзЪДеЫЊжРЬ糥зЃЧж≥ХпЉМеєњж≥ЫеЇФзФ®дЇОжЄЄжИПеЉАеПСдЄ≠зЪДиІТиЙ≤еѓїиЈѓгАБеЬ∞еЫЊеѓЉиИ™з≠ЙйЧЃйҐШгАВеЃГйАЪињЗзїУеРИжЬАдљ≥дЉШеЕИжРЬ糥пЉИBFSпЉЙеТМDijkstraзЃЧж≥ХзЪДдЉШзВєпЉМжЧҐиГљдњЭиѓБжЙЊеИ∞жЬАзЯ≠иЈѓеЊДпЉМеПИиГљжЬЙжХИеЗПе∞СжРЬ糥穯йЧіпЉМжПРйЂШжХИзОЗ...
OrgeпЉИObject-Oriented Graphics Rendering EngineпЉЙжШѓдЄАжђЊеЉЇе§ІзЪД3Dеی嚥жЄ≤жЯУеЉХжУОпЉМиАМA*пЉИA-starпЉЙзЃЧж≥ХеИЩжШѓжЄЄжИПдЄ≠зЪДеѓїиЈѓзЃЧж≥Хй¶ЦйАЙпЉМе∞§еЕґеЬ®еЃЮжЧґз≠ЦзХ•жИЦиІТиЙ≤жЙЃжЉФжЄЄжИПдЄ≠пЉМеЃГз°ЃдњЭдЇЖиІТиЙ≤иГље§ЯењЂйАЯеЗЖз°ЃеЬ∞жЙЊеИ∞зЫЃзЪДеЬ∞гАВ...