- 浏览: 27795 次
- 性别:

- 来自: 杭州
-

文章分类
最新评论
数码相机的定位
此文当时和好友08年参加数学建模时写的,当时大家都是第1次接触计算机图形学,解决方法还是蛮实际的,可惜我们文笔欠佳,不过学习到数码相机的定位原理收获也挺多的
此文内容主要为了解决4个问题,问题如下:
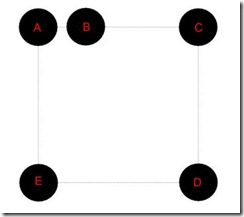
有人设计靶标如下,取1个边长为100mm的正方形,分别以四个顶点(对应为A、C、D、E)为圆心,12mm为半径作圆。以AC边上距离A点30mm处的B为圆心,12mm为半径作圆,如图2所示。
图 2 靶标示意图
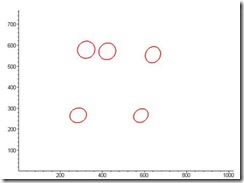
用一位置固定的数码相机摄得其像,如图3所示。
图3 靶标的像
(1) 建立数学模型和算法以确定靶标上圆的圆心在该相机像平面的像坐标, 这里坐标系原点取在该相机的光学中心,x-y平面平行于像平面;
(2) 对由图2、图3分别给出的靶标及其像,计算靶标上圆的圆心在像平面上的像坐标, 该相机的像距(即光学中心到像平面的距离)是1577个像素单位(1毫米约为3.78个像素单位),相机分辨率为1024×768;
(3) 设计一种方法检验你们的模型,并对方法的精度和稳定性进行讨论;
(4) 建立用此靶标给出两部固定相机相对位置的数学模型和方法。
摘要
摄像标定是计算机视觉领域中的一个重要问题,在大多数条件下,空间物体表面某点的三维几何位置与其象图中所对应的坐标之间的相互关系由成像几何模型决定,所以只需求解几何模型参数即可,于是我们通过建立数学模型来求解几何模型以确定参数。
对于问题一:由小孔成像原理,建立针孔模型,通过确定投影矩阵M,可以得到世界坐标系中点与图象坐标系中点的对应关系。由M矩阵就可以算出靶标中圆的圆心在像图中的坐标。为了确定M矩阵,需要靶标上已知点与它们图象点的坐标。因为本题给的靶标是圆,所以不能利用边缘抽取的方法或霍夫变换的方法。这里,根据射影变换的不变性,我们利用靶标上的任意两圆的内公切线交点和其在像图上对应的椭圆内公切线的交点的对应关系,得到10对对应点的坐标作为标定点,从而确定投影矩阵M。
对于问题二:利用Canny边缘检测算法对靶标的原始像图进行处理,得到像图中椭圆的边界点坐标(每个椭圆约200点),再利用最小二乘法原理进行拟合,得到五个椭圆方程。再计算出内公切线交点坐标,确定投影矩阵M。这样得到五个圆圆心在像图中的坐标为:(323.78,577.79),(423.02,570.30),(637.20,554.14),(583.56,264.91),(283.36,265.10)。根据透视投影性质可知,圆心的图像一般不是椭圆的中心。靶标圆心在像中的位置是会随着它们像的形变而发生偏离,我们的结果验证了这一事实。
对于问题三:通过比较靶标中圆在投影矩阵M作用下得到的椭圆和拍摄得到的椭圆的图形,可以检验我们的模型。通过扰动靶标中圆,并对其像图中椭圆发生变化进行比较,可以判定该方法的精度和稳定性较好。
对于问题四:由问题一的投影矩阵M,可以得到照相机的外部参数,即它对于世界坐标系的方位。在同一世界坐标系下,由两个照相机的像图分别求出他们的方位,就可确定这两个相机的相对位置。
针孔模型是线性照相机模型,优点在于原理简单,计算方便,模拟照相生成的图形与拍摄图形符合较好。但是没有考虑照相机镜头的畸变,对于使用广角镜头,远离图象中心处的成像几何关系描述不够准确。
关键词:边缘检测;针孔模型;投影矩阵;最小二乘法;
一 问题的重述
摄像定位是计算机视觉领域中的一个重要问题,最常用的定位方法是双目定位。对物体上一个特征点,用两部固定于不同位置的相机摄得物体的像,分别获得该点在两部相机像平面上的坐标。只要知道两部相机精确的相对位置,就通过几何的方法得到该特征点在固定一部相机的坐标系中的坐标,即确定了特征点的位置。于是对双目定位的关键是如何精确地确定两部相机的相对位置。
平板标定法是其中标定的一种做法是:在一块平板上画若干个点, 同时用这两部相机照相,分别得到这些点在它们像平面上的像点,利用这两组像点的几何关系就可以得到这两部相机的相对位置。然而,无论在物平面或像平面上我们都无法直接得到没有几何尺寸的“点”。实际的做法是在物平面上画若干个圆(称为靶标),它们的圆心就是几何的点了。而它们的像一般会变形,所以必须从靶标上的这些圆的像中把圆心的像精确地找到,标定就可实现。
于是我们需要建立数学模型和算法以确定靶标上圆的圆心在该相机像平面的像坐标, 这里坐标系原点取在该相机的光学中心,x-y平面平行于像平面;然后,计算靶标上圆的圆心在像平面上的像坐标;之后设计一种方法来检验我们的模型,并对此方法的精确度和稳定性进行讨论;最后,建立用此靶标给出两部固定相机相对位置的数学模型和方法。
二 问题的分析及模型假设
2.1 问题的分析
对于第一问,我们需要确定靶标的上圆的圆心在相机像平面中的像坐标,由小孔成像模型知道,物坐标和像坐标之间成比例关系。因此建立世界坐标系,确定世界坐标系与像坐标系的关系是解决第一问的关键。但是本题给的靶标是圆,不能利用边缘抽取的方法或霍夫变换的方法来提取边缘点数据。由于射影变换的不变性,利用靶标上的任意两圆的内公切线交点和其在像图上对应的椭圆内公切线的交点的对应关系。
在第二问中,由于圆心所对应的像坐标不是像的几何中心,对此不能直接使用圆心与像的几何中心的对应关系来求解模型。首先需要利用Canny边缘检测算法对靶标的原始像图进行处理,在得到像图中各个椭圆的边界点坐标后,利用最小二乘法原理进行拟合,得到五个椭圆方程。再分别计算出上述内公切线交点坐标,只用得到8对对应点的坐标作为标定点,就可以确定投影矩阵M,进而确定靶标圆心在像图中的坐标。
在第三问中我们需要设计一种方法来检验模型的可靠性,并分析此方法的精度和稳定性。对此通过比较靶标中圆在投影矩阵M作用下得到的椭圆和拍摄得到的椭圆的图形,以检验我们的模型。通过扰动靶标中圆,并对其像图中椭圆发生的变化进行比较分析,以判断此检验方法的稳定性,并求出精度。
在第四问中考虑二个相机的相互关系时,可以由问题一的投影矩阵M,得到照相机的外部参数,即它对于世界坐标系的方位。在同一世界坐标系下,再由两个照相机的像图分别求出他们的方位,这样就可确定这两个相机的相对位置。
2.2模型假设
1、物点,光心和像点这三点在同一条直线上。
2、不考虑大气因素对成像的影响。
3、不考虑由镜片引起的畸变。
4、假设题目所给图像以及数据是精确可靠的。
2.3模型的数据采集
为了求解模型,我们必须要对靶标的像图做数值化处理,首先将像图格式转化成灰度,根据Canny定义[1],中心边缘点为算子![]() 与图象
与图象![]() 的卷积在边缘梯度方向上的区域中的最大值,于是我们就可以在每一点的梯度方向上判断此点强度是否为其领域的最大值来确定该点是否为边缘点。
的卷积在边缘梯度方向上的区域中的最大值,于是我们就可以在每一点的梯度方向上判断此点强度是否为其领域的最大值来确定该点是否为边缘点。
定义1:如果当一个像素满足以下3个条件时,则可认为是图像的边缘点:
(1)该点的边缘强度大于沿该点梯度方向的两个相邻像素点的边缘强度;
(3)以该点为中心的3×3邻域中的边缘强度极大值小于某个阈值。
如果同时满足定义1中的条件(1)和条件(2),那么在梯度方向上的两个相邻像素就从候选边缘点中取消。而条件(3)则相当于用区域梯度最大值组成的阈值图像与边缘点进行匹配,利用条件(3)我们可以消除很多虚假的边缘点。于是我们利用此算法在Matlab中实现了Canny边缘检测算子程序(具体程序见附录一),如图2所示即为Canny算子检测边缘的结果。由图2中也可以看出,Canny算子检测边缘的优越性。
(图1 靶标的原始像)
(图2 Canny算子提取的边缘图像)
由Canny边缘检测算子处理后的图2数值信息在Matlab中做均值运算还可以得到各椭圆的几何中心坐标:(322.6111,578.5000),(422.6770,571.0044),(638.8267,554.9244),(283.7944,266.2850),(582.2947,264.9526)以及椭圆边缘所有点的坐标数据(具体算法程序见附录一)。
利用Canny算子对图1利用Maple程序leastsqrt得到最小二乘法拟合出A、B、C、D、E的椭圆方程、任意2个椭圆的公切线方程、切点坐标(具体算法程序见附录二)。
|
|
|
|
|
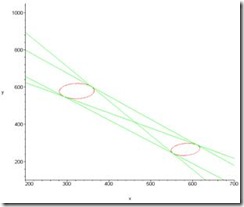
5个椭圆方程图形,见图3:
(图3 像图边缘点的拟合曲线)
三 符号说明
为方便下述模型的分析与讨论,现我们将
水平向右方向表示为坐标系x轴正方向;
垂直向上方向表示为坐标系y轴正方向;
坐标系刻度以1象素为单位。
四 模型的建立与求解
4.1 模型准备
(图4 摄像机成像原理[2])
由物体在摄像机的的成像原理如图可知,一般的![]() ,于是,
,于是,![]() 这时可以将透镜成像模型近似地用小孔模型代替。我们可以用物体在a的投影代替在物体在像片上的像。
这时可以将透镜成像模型近似地用小孔模型代替。我们可以用物体在a的投影代替在物体在像片上的像。
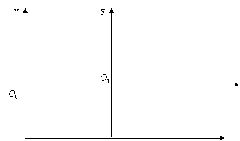
数码相机的图像是以计算机内的一个M*N的数组来储存的M*N个象素值来表示,定义直角坐标系u, v,每个象素的坐标(u,v)分别是该象素值在数组中的列数与行数。所以(u,v)是以象素为单位的的图像坐标系的坐标。如图我们将图像坐标的与现实坐标做个变换,(x,y)是以毫米为单位的图像坐标。原点![]() 定义在摄像机光轴与图像平面的交点,该点一般们于图像的中心处,若
定义在摄像机光轴与图像平面的交点,该点一般们于图像的中心处,若![]() 在u,v坐标系中的坐标为(
在u,v坐标系中的坐标为(![]() ),每个象素在x轴与y轴方向上的物理尺寸为dx,dy,则图像中任意一个象素在一个坐标系下的坐标有如下关系:
),每个象素在x轴与y轴方向上的物理尺寸为dx,dy,则图像中任意一个象素在一个坐标系下的坐标有如下关系:
(图5 图像坐标系)
为接下去的使用方便,我们用齐次坐标与矩阵形式将上式表示为
(1.1)
(1.2)
其逆关系可写成
由于摄像机的位置可任定,我们另选择一个基准坐标系来描述摄像机的位置,并用它来描述环境中任何物体的位置,该坐标系称为世界坐标系。它由![]() 轴组成。摄像机坐标系与世界坐标系之间的关系可以用旋转矩阵R与平移向量t来描述。因此,空间中某一点P在世界坐标系与摄像机坐标系下的齐次坐标如果分别是
轴组成。摄像机坐标系与世界坐标系之间的关系可以用旋转矩阵R与平移向量t来描述。因此,空间中某一点P在世界坐标系与摄像机坐标系下的齐次坐标如果分别是![]() ,于是存在如下关系:
,于是存在如下关系:
(1.3)
(图6 数码相机坐标系和世界坐标系)
4.2 问题一求解
空间任何一点P在图像上的成像位置可以用针孔模型近似表示,即任何点P在图像上的投影位置p,为光心O与P点的连线OP与图像平面的交点。这种关系也称为中心射影或透视投影。由比例关系有如下关系式:
其中,![]() 为
为![]() 点的图解坐标;
点的图解坐标;![]() 为空间点P在摄像机坐标系下的坐标。我们用齐次坐标与矩阵表示上述透视投影关系:
为空间点P在摄像机坐标系下的坐标。我们用齐次坐标与矩阵表示上述透视投影关系:
将式(1,2)与 (1.3) 代入上式,我们得到以世界坐标系表示的P点坐标与其投影点![]() 的坐标
的坐标![]() 的关系:
的关系:
其中,![]() =f/dx,
=f/dx,![]() =f/dy;M为
=f/dy;M为![]() 矩阵,称为投影矩阵;
矩阵,称为投影矩阵;![]() 完全由
完全由![]() ,
,![]() ,
,![]() ,
,![]() 决定,由于
决定,由于![]() ,
,![]() ,
,![]() ,
,![]() 只与相机的内部结构有关,我们称这些参数为相机内部参数;
只与相机的内部结构有关,我们称这些参数为相机内部参数;![]() 完全由摄像机相对于世界坐标系的方位决定,称为相机外部参数。
完全由摄像机相对于世界坐标系的方位决定,称为相机外部参数。
将(1.6)写成
利用靶标上已知点与它们图象点的坐标,求解线性方程组,确定M矩阵后,世界坐标系中的任意点坐标![]() 都可通过(1.9)找到在对应于图像上的坐标,从而问题一得解。
都可通过(1.9)找到在对应于图像上的坐标,从而问题一得解。
4.3 问题二求解
为了确定M矩阵,需要定标点。一般利用边缘抽取的方法或霍夫变换的方法来提取方块图象的边缘点数据,但是本题所给靶标中的图象为圆形,根据射影变换的不变性,我们利用靶标上的任意两圆的内公切线交点和其在像图上对应的椭圆内公切线的交点的对应关系,得到10对对应点的坐标作为标定点,从而确定投影矩阵M。
4.3.1求解算法(以椭圆B和椭圆E为例)
问题二求解步骤如下:
第一步:拟合出椭圆B和椭圆E的方程。
第二步:设切线方程为![]() ,将切线方程代入椭圆方程B和椭圆方程E。
,将切线方程代入椭圆方程B和椭圆方程E。
第五步:重复上述步骤,计算出其他相交内切线的交点坐标,我们一共可以得到![]() 个内切点坐标(椭圆A和D的内切线交点与椭圆C和E的内切线交点重合)。
个内切点坐标(椭圆A和D的内切线交点与椭圆C和E的内切线交点重合)。
第六步:将其中的8个坐标代入方程![clip_image123[1] clip_image123[1]](http://hi.csdn.net/attachment/201101/26/0_1296022731H9no.gif) ,
,![]() ,并求解出方程组的所有参量。
,并求解出方程组的所有参量。
第七步:在世界坐标系中确定靶标的圆心坐标,通过方程组计算得到对应图象中的坐标。
(图7 只保留椭圆B和椭圆E的像图)
从第一步到第四步,可以解得切线y=5.186793326x-1413.149178和y=1.309821741x-46.63798186交点G(415.0332052, 352.4687159)
第五步后,可以解得各个内切线交点坐标(373.66,574.33),(533.13,562.49),(485.52,565.99),(610.41,404.79),(507.82,408.42),(438.78,265.35),(462.40,409.98),(352.46,415.03),(303.22,416.98)。
经过第六步,解得m32 =![]() , m22 = 2.863338902, m21 =0.1545733139, m24 = 204.7993333, m31 =
, m22 = 2.863338902, m21 =0.1545733139, m24 = 204.7993333, m31 =![]() , m12 = 0.2526671371, m11 = 3.434352961, m14 = 210.3224771。
, m12 = 0.2526671371, m11 = 3.434352961, m14 = 210.3224771。
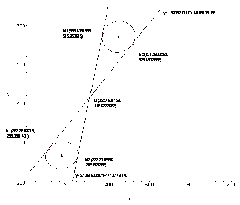
第七步之后的解如图7和图8所示,圆心坐标![]() (20,120),
(20,120),![]() (50,120),
(50,120),![]() (120,120),
(120,120),![]() (120,20),
(120,20),![]() (20,20)所对应的像中心坐标即为
(20,20)所对应的像中心坐标即为 ![]() (323.78,577.79),
(323.78,577.79), ![]() (423.02,570.30),
(423.02,570.30),![]() (637.20,554.14),
(637.20,554.14),![]() (583.56,264.91),
(583.56,264.91), ![]() (283.36,265.10)。
(283.36,265.10)。
(注:具体求解算法程序见程序文件)
(图8 标靶中心坐标图)
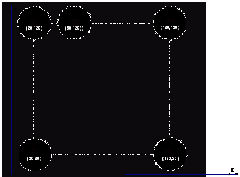
(图9 像中心坐标图)
图9中![]() 为椭圆几何中心坐标,
为椭圆几何中心坐标,![]() 为靶标圆心在像中的坐标。从图中可以看出用椭圆几何中心作为靶标圆心在像图中的像点是有误差的。且图象形变程度越大这两点的误差越大。和射影几何的理论结果以及实际照相经验符合。
为靶标圆心在像中的坐标。从图中可以看出用椭圆几何中心作为靶标圆心在像图中的像点是有误差的。且图象形变程度越大这两点的误差越大。和射影几何的理论结果以及实际照相经验符合。
4.4 问题三求解
在问题一的求解时我们建立模型得到关系式(1.9):
我们对于靶标中边界上所有点都离散,再通过关系式(1.9)还原它在图像上的点。比较它与原图的差别检验模型的好坏。(过程见程序);
(图10 模型校验图)
图10中,散点为靶标中圆周上的点在像中的点,连续的曲线为数据采集时建立的椭圆曲线。通过肉眼观察,其精度较高。现我们通过对散点拟和,得到新的椭圆曲线,与原曲线比较,进一步讨论其精度。具体过程如下:
第一步:利用最小二乘法拟合出新的椭圆曲线:
第二步:分别用原来的椭圆方程与新的椭圆方程相减。
第三步:把散点的坐标代入第二步所得的式子,并求其方差。则如果方差小,其的精度就高,说明对问题一和二建立的模型的稳定性差。返之,亦然。
从第一步中得到椭圆方程如下:
| |
| |
|
|
|
通过第二步、第三步的运算,得到5对原椭圆方程与新椭圆方程的方差:
由上可见,所得的结果的精度高,可信度强,与图10的直观吻合。
4.5 问题四求解
(图11 双摄像机几何关系)
如(图11)用两个摄像机同时观察周围环境,在定标中我们可以用单摄像机定标方法得各自摄像机的外参数,即R、t。在这里我们用![]() 分别表示摄像
分别表示摄像![]() 相对于世界坐标系的旋转矩阵和平移向量
相对于世界坐标系的旋转矩阵和平移向量![]() 分别表示摄像机
分别表示摄像机![]() 相对于世界坐标系的旋转矩阵和平移向量。从第一个模型中我们可以得到如下的两个方程:
相对于世界坐标系的旋转矩阵和平移向量。从第一个模型中我们可以得到如下的两个方程:
因此,两个摄像机之间的几何关系可用以下R和t表示:
从上面的论述中知道R和t是由M分解而来,所以要确定摄像机![]() 和
和 ![]() 的相对位置只要求得各摄像机相对于世界坐标系的M矩阵。
的相对位置只要求得各摄像机相对于世界坐标系的M矩阵。
五 模型的评价
本文用针孔成像模型描述空间物体在像图中成像的对应关系,是照相机线性模型,对这个模型进行定标,需要求解的是线性方程,简单快速。在解决问题二的时候,可以看出用椭圆几何中心作为靶标圆心在像图中的像点是有误差的。且图像形变程度越大这两点的误差越大。和射影几何的理论结果以及实际照相经验符合。应用解决问题二得到的射影矩阵,可以得到靶标中圆在投影矩阵M作用下得到的椭圆,比较和拍摄得到的椭圆的图形,发现二者比较接近。说明该模型具有一定的准确性。
该模型的缺点是没有考虑照相机镜头的畸变,对于使用广角镜头,远离图象中心处的成像几何关系描述不够准确。可以采用非线性模型进行处理,因为时间关系,本文没有处理。
参考文献
[1] 欧珊瑚,王倩丽,朱哲瑜,Visual C++.net数字图像处理技术与应用,北京:清华大学出版社,2004年,第418页。
[2] 马颂德,张正友,计算机视觉:计算理论与算法基础,北京:科学出版社,1998年,第22页。
[3] 高文,陈熙霖,计算机视觉:算法与系统理论,北京:清华大学出版社,2000年。
[4] 王沫然, MATLAB与科学计算,北京:电子工业出版社, 2004年。
[5] 姜大志,孙闵,刘淼,姜梅,丁秋林,数码相机标定方法研究,南京航空航天大学学报,Vol.33 No.1,2001年2月。
附录一
%程序文件名为bianyuan.m
%此程序功能基于Canny算子边缘检测法检测二值图象边缘,并利用边缘点数据计算几何中心坐标(Matlab实现)
clc
[A,map]=imread('bianyuan.tif');
figure,imshow(A),title('原图象');
%用edge()的Canny算子对其进行边缘检测
BW1=edge(A,'canny');
figure,hold on,imshow(BW1);
title('只保留边缘的图象');hold off;
B=BW1;%矩阵B存储边缘点信息
display(sum(sum(B)));
x=[0 0 0 0 0 0];
y=[0 0 0 0 0 0];
count=[0 0 0 0 0 0];
%以下过程计算椭圆几何中心
for i=1:342
for j=1:374
if(B(i,j)>0)
x(1)=x(1)+j;
y(1)=y(1)+i;
count(1)=count(1)+1;
end
end
end
for i=1:342
for j=374:512
if(B(i,j)>0)
x(2)=x(2)+j;
y(2)=y(2)+i;
count(2)=count(2)+1;
end
end
end
for i=1:342
for j=512:1024
if(B(i,j)>0)
x(3)=x(3)+j;
y(3)=y(3)+i;
count(3)=count(3)+1;
end
end
end
for i=342:768
for j=1:374
if(B(i,j)>0)
x(4)=x(4)+j;
y(4)=y(4)+i;
count(4)=count(4)+1;
end
end
end
for i=342:768
for j=374:512
if(B(i,j)>0)
x(5)=x(5)+j;
y(5)=y(5)+i;
count(5)=count(5)+1;
end
end
end
for i=342:768
for j=512:1024
if(B(i,j)>0)
x(6)=x(6)+j;
y(6)=y(6)+i;
count(6)=count(6)+1;
end
end
end
for k=1:6
x(k)=x(k)/count(k);
y(k)=786-y(k)/count(k);
display(x);display(y);
end
附录二
> with(plots):
> AT:=104486170931771690231802905713711/45121927305732678291574003178337319940*x^2+324522499876003788843792179043787/135365781917198034874722009535011959820*y^2-2375494240459540339070392917574/11280481826433169572893500794584329985*x*y-185834502855123115947799772896368563/135365781917198034874722009535011959820*x-30519857067727329965449289549723287/11280481826433169572893500794584329985*y+1:
> BT:=44401919564607433738373614231660/20887987587661253647544634634786618463*x^2+44463749588501254900597630857204/20887987587661253647544634634786618463*y^2-6120910378551219052841646868245/20887987587661253647544634634786618463*x*y-34054771298838591777643601210557371/20887987587661253647544634634786618463*x-48191291321889301069368629550116073/20887987587661253647544634634786618463*y+1:
> CT:=174313302154510257599068307937168/103605696214343535963571605242565501553*x^2+305845186259855813428805594587699/207211392428687071927143210485131003106*y^2-40965095182694965560843607939486/103605696214343535963571605242565501553*x*y-200237719648877500595153575562700257/103605696214343535963571605242565501553*x-286964755026757994043880855047322341/207211392428687071927143210485131003106*y+1:
> DT:=2977459628014358380055658971800/1067742005143610664751459529091780679*x^2+3303746415348748303946471296155/1067742005143610664751459529091780679*y^2-1111414098972026311113944952442/1067742005143610664751459529091780679*x*y-3174811472523972327597547930826481/1067742005143610664751459529091780679*x-1104022161363564787497658920491925/1067742005143610664751459529091780679*y+1:
> ET:=15723757168921279348585078085797/2404774876728384837645797754428891683*x^2+19951797564862664608935325619424/2404774876728384837645797754428891683*y^2-3394528274772759462445373240802/2404774876728384837645797754428891683*x*y-8039456320588351303388334548879629/2404774876728384837645797754428891683*x-9659102641840513058373332919557295/2404774876728384837645797754428891683*y+1:
>
> ggg1:=implicitplot(BT,x=360..480,y=500..620,view=[1..1024,1..768],thickness=2):
ggg2:=implicitplot(ET,x=220..350,y=220..320,view=[1..1024,1..768],thickness=2):
ggg3:=implicitplot(AT,x=200..500,y=500..700,view=[1..1024,1..768],thickness=2):
ggg4:=implicitplot(CT,x=500..690,y=500..600,view=[1..1024,1..768],thickness=2):
ggg5:=implicitplot(DT,x=500..650,y=200..300,view=[1..1024,1..768],thickness=2):
display(ggg1,ggg2,ggg3,ggg4,ggg5);
> myproc:=proc(eq1,eq2)
local eqa1,eqa2,eqns,vars,b,a,i;
eqa1:=collect(subs(y=m*x+n,eq1),x);
eqa2:=collect(subs(y=m*x+n,eq2),x);
eqns:={discrim(eqa1,x)=0,discrim(eqa2,x)=0};
vars:={m,n};b:={};a:=solve(eqns,vars);
for i from 1 to nops({a}) do if type(subs(a[i],n),numeric) then b:=b union {a[i]} fi; od;
return b;
end:
> myproc(evalf(BT),evalf(CT));
> with(plots);AD:=implicitplot(DT,x=540..630,y=200..300):
> AD1:=implicitplot(AT,x=280..380,y=500..650):display(AD);
> admn:=myproc(evalf(AT),evalf(DT));
> ADL:=plot({seq(subs(admn[i],m*x+n),i=1..4)},x=200..700,y=100..1050,color=green):
> display(ADL,AD,AD1);
> b:=seq(subs(admn[i],m*x+n),i=1..4);
> solve({b[1]=y,b[4]=y},{x,y});
BD
> with(plots);BD:=implicitplot(DT,x=540..630,y=200..300):
> BD1:=implicitplot(BT,x=380..480,y=530..620):display(BD1);
> bdmn:=myproc(evalf(BT),evalf(DT));
> BDL:=plot({seq(subs(bdmn[i],m*x+n),i=5)},x=200..700,y=100..1050,color=green):bdmn[5];
> display(BDL,BD,BD1);
> b:=seq(subs(bdmn[i],m*x+n),i=1..5);b[1];
> solve({b[1]=y,b[5]=y},{x,y});
BE
> with(plots);BE:=implicitplot(ET,x=200..330,y=220..310):
> BE1:=implicitplot(BT,x=380..480,y=530..620):display(BE);
> bemn:=myproc(evalf(BT),evalf(ET));
> BEL:=plot({seq(subs(bemn[i],m*x+n),i=3)},x=200..700,y=100..1050,color=green):
> display(BEL,BE,BE1);
> b:=seq(subs(bemn[i],m*x+n),i=1..4);b[1];
> solve({b[3]=y,b[4]=y},{x,y});
CE
> with(plots);CE:=implicitplot(ET,x=200..330,y=220..310):
> CE1:=implicitplot(CT,x=590..700,y=510..800):display(CE1);
> cemn:=myproc(evalf(CT),evalf(ET));
> CEL:=plot({seq(subs(cemn[i],m*x+n),i=2)},x=200..700,y=100..1050,color=green):
> display(CEL,CE,CE1);
> b:=seq(subs(cemn[i],m*x+n),i=1..4);b[1];
> solve({b[2]=y,b[3]=y},{x,y});








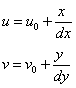
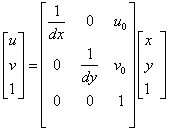
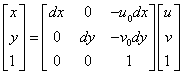
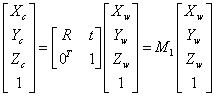

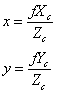
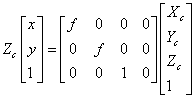
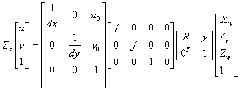
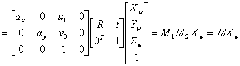

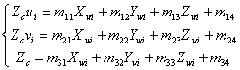
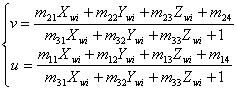

![clip_image123[2] clip_image123[2]](http://hi.csdn.net/attachment/201101/26/0_1296022743qDSi.gif)




相关推荐
《数码相机定位算法研究》这篇论文是针对2008年A题数学建模的一份研究,主要探讨了如何在数码相机系统中精确地实现定位技术。数学建模在解决实际问题时,常通过建立数学模型来分析和解决问题,本论文就是将这种理论...
【数码相机定位剖析】 数码相机定位技术在交通监控、自动驾驶等多个领域有着广泛的应用。它主要依赖于双目定位,即通过两台相机从不同角度拍摄同一物体,利用几何原理来确定物体特征点在三维空间中的位置。关键在于...
标题中的“数学建模-07B【数码相机定位问题】-全国一等奖”指的是一个关于数学建模的项目,这个项目特别关注数码相机在空间中的定位问题,并且获得了全国一等奖的荣誉。数学建模是应用数学解决实际问题的一种方法,...
【数码相机定位剖析】 数码相机定位技术在交通监控、电子警察等领域有着广泛的应用。它主要通过分析数码相机拍摄的照片来确定物体表面特定特征点的位置。本文重点探讨的是双目定位方法,即使用两台相机从不同角度...
对数码相机定位问题进行了较深入的研究。 针对问题一和二,我们建立了两种不同模型——变换矩阵模型和公切线模 型。在变换矩阵模型中,建立了物、像、相机三个坐标系,分别称为世界坐标系, 像坐标系和光心坐标系。...
【数码相机定位】是计算机视觉领域的一个重要课题,主要涉及摄像机成像的几何模型以及参数标定。在2008年的全国大学生数学建模竞赛中,这个问题被提出,目的是通过数学模型来确定数码相机拍摄物体时,物体特征点在...
《数码相机定位技术详解》 数码相机定位是现代信息技术中不可或缺的一部分,特别是在交通监管、航天研究和城市建设等领域,它的应用日益广泛。本文主要探讨的是如何通过数学建模和软件工具来解决数码相机的定位问题...
数码相机作为一种常见的摄影设备,在各个领域中扮演着重要角色,特别是在交通监控、机器人导航等领域,其定位功能的准确性直接关系到系统的可靠性。针对数码相机定位问题,本文深入研究了影响其定位精度的因素,并...
在当代信息技术迅速发展的背景下,数码相机作为信息获取的重要工具之一,其定位技术的精确性对于图像处理和计算机视觉领域具有重要意义。《数码相机定位模型》这篇论文针对数学建模竞赛中的数码相机定位问题进行了...
### 数码相机定位技术及其应用 #### 一、背景介绍 随着信息技术的发展,数码相机不仅在个人消费领域有着广泛的应用,而且在专业领域如交通监控、安全监管等场景也发挥着重要作用。特别是在交通监管领域,如电子...
"数学建模-07B【数码相机定位问题】-北京二等奖"这一标题揭示了这个压缩包内容的主题。首先,“数学建模”是指应用数学的方法来解决实际问题的过程,它通常涉及概率统计、线性代数、微积分等数学工具。在这个特定的...
### 数码相机定位的系统标定模型 #### 模型概览 本文旨在探讨数码相机定位中的系统标定问题,具体来说,是如何通过对靶标上圆心及其在图像中的成像进行几何关系的研究来获得像的具体坐标以及两部相机间的精确相对...
【数码相机定位】是计算机视觉领域的一个重要概念,主要涉及如何通过数码相机拍摄的图像来确定物体表面特征点的位置。在【2008年全国大学生数学建模竞赛A题优秀论文】中,作者深入研究了这一问题,尤其是在交通监控...
2008年的A题聚焦于“数码相机定位”,这是一个涉及数学、计算机科学和图像处理的实际问题。在这个题目中,参赛者需要利用数学模型来解决如何准确地定位数码相机在三维空间中的位置。 数学建模在这个问题上起着至关...
### 数码相机定位研究 #### 一、引言 数码相机定位技术是计算机视觉领域的重要研究方向之一,它涉及到如何利用数码相机拍摄的图像来精确地确定物体在三维空间中的位置。本文主要探讨了数码相机定位模型的实现,...
数码相机定位为研究对象,重点研究圆形目标检测和摄像机标定这两方面,对数码相机进行精确定位。