https://zhuanlan.zhihu.com/p/32626442
ж•Фе≠Р
еЙНдЇЫжЧ•еЬ®еЖЩиЃ°зЃЧжХ∞е≠¶иѓЊзЪДжЬЯжЬЂиѓїдє¶жК•еСКпЉМжИСйАЙжЛ©зЪДдЄїйҐШжШѓгАМеИЖжЮРжЈ±еЇ¶е≠¶дє†дЄ≠зЪДеРДдЄ™дЉШеМЦзЃЧж≥ХгАНгАВеЬ®ж≠§еЙНзЪДеЈ•дљЬдЄ≠пЉМиЗ™еЈ±йАЪеЄЄе∞±жШѓжЧ†иДСгАМAdam е§Іж≥Хе•љгАНпЉМиАМеѓєзЃЧж≥ХжЬђиЇЂзЪДеЖЕжґµдЄНзЯ•жЙАдї•зДґгАВдЄАзЫіеЄМжЬЫиГљжКљжЧґйЧіз≥їзїЯзЪДињЗдЄАйБНдЉШеМЦзЃЧж≥ХзЪДеПСе±ХеОЖз®ЛпЉМзЫіиІВдЇЖиІ£еРДдЄ™зЃЧж≥ХзЪДйХње§ДеТМзЯ≠е§ДгАВињЩжђ°ж≠£е•љеАЯзЭАдљЬдЄЪзЪДжЬЇдЉЪпЉМи°•дЄАи°•иѓЊгАВ
жЬђжЦЗдЄїи¶БеАЯйЙідЇЖ¬†
¬†зЪДжЦЗзЂ†[1]жАЭиЈѓпЉМдљњзФ®дЄАдЄ™ general зЪДж°ЖжЮґжЭ•жППињ∞еРД䪙楃寶дЄЛйЩНеПШзІНзЃЧж≥ХгАВеЃЮйЩЕдЄКпЉМжЬђжЦЗеПѓдї•иІЖдљЬеѓє[1]зЪДйЗНињ∞пЉМеЬ®ж≠§еЯЇз°АдЄКпЉМеѓєеОЯжЦЗжППињ∞дЄНе§Яиѓ¶е∞љзЪДйГ®еИЖеБЪдЇЖдЄАеЃЪи°•еЕЕпЉМеєґдњЃж≠£дЇЖеЕґдЄ≠иЃЄе§ЪйФЩиѓѓзЪДи°®ињ∞еТМеЕђеЉПгАВ¬†
еП¶дЄАдЄїи¶БеПВиАГжЦЗзЂ†жШѓ Sebastian Ruder зЪДзїЉињ∞[2]гАВиѓ•жЦЗеНБеИЖжЬЙеРНпЉМе§Іж¶ВжШѓжЈ±еЇ¶е≠¶дє†дЉШеМЦзЃЧж≥ХзїЉињ∞дЄ≠иі®йЗПжЬАе•љзЪДдЄАзѓЗдЇЖгАВеїЇиЃЃе§ІеЃґеПѓдї•зЫіжО•йШЕиѓїеОЯжЦЗгАВжЬђжЦЗиЃЄе§ЪзїУиЃЇеТМжПТеЫЊеЉХиЗ™иѓ•зїЉињ∞гАВ
еѓєдЉШеМЦзЃЧж≥ХињЫи°МеИЖжЮРеТМжѓФиЊГзЪДжЦЗзЂ†еЈ≤жЬЙ姙е§ЪпЉМжЬђжЦЗеЃЮеЬ®еП™иГљзЃЧеЊЧдЄКжШѓйЗНе§НйА†иљЃпЉМжЧ®еЬ®дЄ™дЇЇе≠¶дє†еТМжАїзїУгАВеЄМжЬЫеѓєдЉШеМЦзЃЧж≥ХжЬЙжЈ±еЕ•дЇЖиІ£зЪДеРМе≠¶еПѓдї•зЫіжО•жЯ•йШЕжЦЗжЬЂзЪДеПВиАГжЦЗзМЃгАВ
еЉХи®А
жЬАдЉШеМЦйЧЃйҐШжШѓиЃ°зЃЧжХ∞е≠¶дЄ≠жЬАдЄЇйЗНи¶БзЪДз†Фз©ґжЦєеРСдєЛдЄАгАВиАМеЬ®жЈ±еЇ¶е≠¶дє†йҐЖеЯЯпЉМдЉШеМЦзЃЧж≥ХзЪДйАЙжЛ©дєЯжШѓдЄАдЄ™ж®°еЮЛзЪДйЗНдЄ≠дєЛйЗНгАВеН≥дљњеЬ®жХ∞жНЃйЫЖеТМж®°еЮЛжЮґжЮДеЃМеЕ®зЫЄеРМзЪДжГЕеЖµдЄЛпЉМйЗЗзФ®дЄНеРМзЪДдЉШеМЦзЃЧж≥ХпЉМдєЯеЊИеПѓиГљеѓЉиЗіжИ™зДґдЄНеРМзЪДиЃ≠зїГжХИжЮЬгАВ
楃寶дЄЛйЩНжШѓзЫЃеЙНз•ЮзїПзљСзїЬдЄ≠дљњзФ®жЬАдЄЇеєњж≥ЫзЪДдЉШеМЦзЃЧж≥ХдєЛдЄАгАВдЄЇдЇЖеЉ•и°•жܳ糆楃寶дЄЛйЩНзЪДзІНзІНзЉЇйЩЈпЉМз†Фз©ґиАЕдїђеПСжШОдЇЖдЄАз≥їеИЧеПШзІНзЃЧж≥ХпЉМдїОжЬАеИЭзЪД SGD (йЪПжܯ楃寶дЄЛйЩН) йАРж≠•жЉФињЫеИ∞ NAdamгАВзДґиАМпЉМиЃЄе§Ъе≠¶жЬѓзХМжЬАдЄЇеЙНж≤њзЪДжЦЗзЂ†дЄ≠пЉМйГљеєґж≤°жЬЙдЄАеС≥дљњзФ® Adam/NAdam з≠ЙеЕђиЃ§вАЬе•љзФ®вАЭзЪДиЗ™йАВеЇФзЃЧж≥ХпЉМеЊИе§ЪзФЪиЗ≥ињШйАЙжЛ©дЇЖжЬАдЄЇеИЭзЇІзЪД SGD жИЦиАЕ SGD with Momentum з≠ЙгАВ
жЬђжЦЗжЧ®еЬ®жҐ≥зРЖжЈ±еЇ¶е≠¶дє†дЉШеМЦзЃЧж≥ХзЪДеПСе±ХеОЖз®ЛпЉМеєґеЬ®дЄАдЄ™жЫіеК†ж¶ВжЛђзЪДж°ЖжЮґдєЛдЄЛпЉМеѓєдЉШеМЦзЃЧж≥ХеБЪеЗЇеИЖжЮРеТМеѓєжѓФгАВ
Gradient Descent
楃寶дЄЛйЩНжШѓжМЗпЉМеЬ®зїЩеЃЪеЊЕдЉШеМЦзЪДж®°еЮЛеПВжХ∞¬†¬†еТМзЫЃж†ЗеЗљжХ∞¬†
¬†еРОпЉМзЃЧж≥ХйАЪињЗж≤њжҐѓеЇ¶¬†
¬†зЪДзЫЄеПНжЦєеРСжЫіжЦ∞¬†
¬†жЭ•жЬАе∞ПеМЦ¬†
¬†гАВе≠¶дє†зОЗ¬†
¬†еЖ≥еЃЪдЇЖжѓПдЄАжЧґеИїзЪДжЫіжЦ∞ж≠•йХњгАВеѓєдЇОжѓПдЄАдЄ™жЧґеИї¬†
¬†пЉМжИСдїђеПѓдї•зФ®дЄЛињ∞ж≠•й™§жППињ∞楃寶дЄЛйЩНзЪДжµБз®ЛпЉЪ
(1) иЃ°зЃЧзЫЃж†ЗеЗљжХ∞еЕ≥дЇОеПВжХ∞зЪД楃寶
(2) ж†єжНЃеОЖеП≤楃寶聰зЃЧдЄАйШґеТМдЇМйШґеК®йЗП
(3) жЫіжЦ∞ж®°еЮЛеПВжХ∞
еЕґдЄ≠пЉМ¬†¬†дЄЇеє≥жїСй°єпЉМйШ≤ж≠ҐеИЖжѓНдЄЇйЫґпЉМйАЪеЄЄеПЦ 1e-8гАВ
Gradient Descent еТМеЕґзЃЧж≥ХеПШзІН
ж†єжНЃдї•дЄКж°ЖжЮґпЉМжИСдїђжЭ•еИЖжЮРеТМжѓФиЊГ楃寶дЄЛйЩНзЪДеРДеПШзІНзЃЧж≥ХгАВ
Vanilla SGD
жЬізі† SGD (Stochastic Gradient Descent) жЬАдЄЇзЃАеНХпЉМж≤°жЬЙеК®йЗПзЪДж¶ВењµпЉМеН≥
ињЩжЧґпЉМжЫіжЦ∞ж≠•й™§е∞±жШѓжЬАзЃАеНХзЪД
SGD зЪДзЉЇзВєеЬ®дЇОжФґжХЫйАЯеЇ¶жЕҐпЉМеПѓиГљеЬ®йЮНзВєе§ДйЬЗиН°гАВеєґдЄФпЉМе¶ВдљХеРИзРЖзЪДйАЙжЛ©е≠¶дє†зОЗжШѓ SGD зЪДдЄАе§ІйЪЊзВєгАВ
Momentum
SGD еЬ®йБЗеИ∞ж≤Яе£СжЧґеЃєжШУйЩЈеЕ•йЬЗиН°гАВдЄЇж≠§пЉМеПѓдї•дЄЇеЕґеЉХеЕ•еК®йЗП Momentum[3]пЉМеК†йАЯ SGD еЬ®ж≠£з°ЃжЦєеРСзЪДдЄЛйЩНеєґжКСеИґйЬЗиН°гАВ
SGD-M еЬ®еОЯж≠•йХњдєЛдЄКпЉМеҐЮеК†дЇЖдЄОдЄКдЄАжЧґеИїж≠•йХњзЫЄеЕ≥зЪД¬†¬†пЉМ
¬†йАЪеЄЄеПЦ 0.9 еЈ¶еП≥гАВињЩжДПеС≥зЭАеПВжХ∞жЫіжЦ∞жЦєеРСдЄНдїЕзФ±ељУеЙНзЪД楃寶еЖ≥еЃЪпЉМдєЯдЄОж≠§еЙНзіѓзІѓзЪДдЄЛйЩНжЦєеРСжЬЙеЕ≥гАВињЩдљњеЊЧеПВжХ∞дЄ≠йВ£дЇЫ楃寶жЦєеРСеПШеМЦдЄНе§ІзЪДзїіеЇ¶еПѓдї•еК†йАЯжЫіжЦ∞пЉМеєґеЗПе∞С楃寶жЦєеРСеПШеМЦиЊГе§ІзЪДзїіеЇ¶дЄКзЪДжЫіжЦ∞еєЕеЇ¶гАВзФ±ж≠§дЇІзФЯдЇЖеК†йАЯжФґжХЫеТМеЗПе∞ПйЬЗиН°зЪДжХИжЮЬгАВ
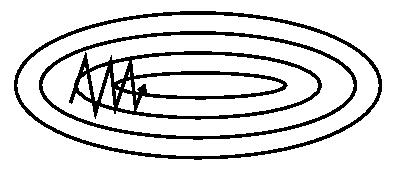 еЫЊ 1(a): SGD
еЫЊ 1(a): SGD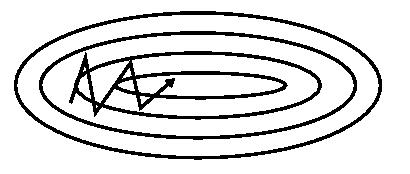 еЫЊ 1(b): SGD with momentum
еЫЊ 1(b): SGD with momentum
дїОеЫЊ 1 дЄ≠еПѓдї•зЬЛеЗЇпЉМеЉХеЕ•еК®йЗПжЬЙжХИзЪДеК†йАЯдЇЖ楃寶дЄЛйЩНжФґжХЫињЗз®ЛгАВ
Nesterov Accelerated Gradient
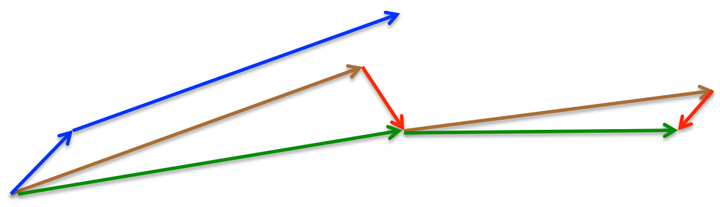 еЫЊ 2: Nesterov update
еЫЊ 2: Nesterov update
жЫіињЫдЄАж≠•зЪДпЉМдЇЇдїђеЄМжЬЫдЄЛйЩНзЪДињЗз®ЛжЫіеК†жЩЇиГљпЉЪзЃЧж≥ХиГље§ЯеЬ®зЫЃж†ЗеЗљжХ∞жЬЙеҐЮйЂШиґЛеКњдєЛеЙНпЉМеЗПзЉУжЫіжЦ∞йАЯзОЗгАВ
NAG еН≥жШѓдЄЇж≠§иАМиЃЊиЃ°зЪДпЉМеЕґеЬ® SGD-M зЪДеЯЇз°АдЄКињЫдЄАж≠•жФєињЫдЇЖж≠•й™§ 1 дЄ≠зЪД楃寶聰зЃЧеЕђеЉПпЉЪ
еПВиАГеЫЊ 2пЉМSGD-M зЪДж≠•йХњиЃ°зЃЧдЇЖељУеЙН楃寶пЉИзЯ≠иУЭеРСйЗПпЉЙеТМеК®йЗПй°є пЉИйХњиУЭеРСйЗПпЉЙгАВзДґиАМпЉМжЧҐзДґеЈ≤зїПеИ©зФ®дЇЖеК®йЗПй°єжЭ•жЫіжЦ∞ пЉМйВ£дЄН嶮еЕИиЃ°зЃЧеЗЇдЄЛдЄАжЧґеИї¬†¬†зЪДињСдЉЉдљНзљЃ пЉИж£ХеРСйЗПпЉЙпЉМеєґж†єжНЃиѓ•жЬ™жЭ•дљНзљЃиЃ°зЃЧ楃寶пЉИзЇҐеРСйЗПпЉЙпЉМзДґеРОдљњзФ®еТМ SGD-M дЄ≠зЫЄеРМзЪДжЦєеЉПиЃ°зЃЧж≠•йХњпЉИзїњеРСйЗПпЉЙгАВињЩзІНиЃ°зЃЧ楃寶зЪДжЦєеЉПеПѓдї•дљњзЃЧж≥ХжЫіе•љзЪДгАМйҐДжµЛжЬ™жЭ•гАНпЉМжПРеЙНи∞ГжХіжЫіжЦ∞йАЯзОЗгАВ
Adagrad
SGDгАБSGD-M еТМ NAG еЭЗжШѓдї•зЫЄеРМзЪДе≠¶дє†зОЗеОїжЫіжЦ∞¬†¬†зЪДеРДдЄ™еИЖйЗПгАВиАМжЈ±еЇ¶е≠¶дє†ж®°еЮЛдЄ≠еЊАеЊАжґЙеПКе§ІйЗПзЪДеПВжХ∞пЉМдЄНеРМеПВжХ∞зЪДжЫіжЦ∞йҐСзОЗеЊАеЊАжЬЙжЙАеМЇеИЂгАВеѓєдЇОжЫіжЦ∞дЄНйҐСзєБзЪДеПВжХ∞пЉИеЕЄеЮЛдЊЛе≠РпЉЪжЫіжЦ∞ word embedding дЄ≠зЪДдљОйҐСиѓНпЉЙпЉМжИСдїђеЄМжЬЫеНХжђ°ж≠•йХњжЫіе§ІпЉМе§Ъе≠¶дє†дЄАдЇЫзЯ•иѓЖпЉЫеѓєдЇОжЫіжЦ∞йҐСзєБзЪДеПВжХ∞пЉМжИСдїђеИЩеЄМжЬЫж≠•йХњиЊГе∞ПпЉМдљњеЊЧе≠¶дє†еИ∞зЪДеПВжХ∞жЫіз®≥еЃЪпЉМдЄНиЗ≥дЇО襀еНХдЄ™ж†ЈжЬђељ±еУН姙е§ЪгАВ
Adagrad[4] зЃЧж≥ХеН≥еПѓиЊЊеИ∞ж≠§жХИжЮЬгАВеЕґеЉХеЕ•дЇЖдЇМйШґеК®йЗПпЉЪ
еЕґдЄ≠пЉМ¬†¬†жШѓеѓєиІТзЯ©йШµпЉМеЕґеЕГзі†¬†
¬†дЄЇеПВжХ∞зђђ¬†
¬†зїідїОеИЭеІЛжЧґеИїеИ∞жЧґеИї¬†
¬†зЪД楃寶еє≥жЦєеТМгАВ
ж≠§жЧґпЉМеПѓдї•ињЩж†ЈзРЖиІ£пЉЪе≠¶дє†зОЗз≠ЙжХИдЄЇ¬†¬†гАВеѓєдЇОж≠§еЙНйҐСзєБжЫіжЦ∞ињЗзЪДеПВжХ∞пЉМеЕґдЇМйШґеК®йЗПзЪДеѓєеЇФеИЖйЗПиЊГе§ІпЉМе≠¶дє†зОЗе∞±иЊГе∞ПгАВињЩдЄАжЦєж≥ХеЬ®з®АзЦПжХ∞жНЃзЪДеЬЇжЩѓдЄЛи°®зО∞еЊИе•љгАВ
RMSprop
еЬ® Adagrad дЄ≠пЉМ¬†¬†жШѓеНХи∞ГйАТеҐЮзЪДпЉМдљњеЊЧе≠¶дє†зОЗйАРжЄРйАТеЗПиЗ≥ 0пЉМеПѓиГљеѓЉиЗіиЃ≠зїГињЗз®ЛжПРеЙНзїУжЭЯгАВдЄЇдЇЖжФєињЫињЩдЄАзЉЇзВєпЉМеПѓдї•иАГиЩСеЬ®иЃ°зЃЧдЇМйШґеК®йЗПжЧґдЄНзіѓзІѓеЕ®йГ®еОЖеП≤楃寶пЉМиАМеП™еЕ≥ж≥®жЬАињСжЯРдЄАжЧґйЧіз™ЧеП£еЖЕзЪДдЄЛйЩН楃寶гАВж†єжНЃж≠§жАЭжГ≥жЬЙдЇЖ RMSprop[5]гАВиЃ∞¬†
¬†дЄЇ¬†
¬†пЉМжЬЙ
еЕґдЇМйШґеК®йЗПйЗЗзФ®жМЗжХ∞зІїеК®еє≥еЭЗеЕђеЉПиЃ°зЃЧпЉМињЩж†ЈеН≥еПѓйБњеЕНдЇМйШґеК®йЗПжМБзї≠зіѓзІѓзЪДйЧЃйҐШгАВеТМ SGD-M дЄ≠зЪДеПВжХ∞з±їдЉЉпЉМ¬†йАЪеЄЄеПЦ 0.9 еЈ¶еП≥гАВ
Adadelta
еЊЕи°•еЕЕ
Adam
Adam[6] еПѓдї•иЃ§дЄЇжШѓ RMSprop еТМ Momentum зЪДзїУеРИгАВеТМ RMSprop еѓєдЇМйШґеК®йЗПдљњзФ®жМЗжХ∞зІїеК®еє≥еЭЗз±їдЉЉпЉМAdam дЄ≠еѓєдЄАйШґеК®йЗПдєЯжШѓзФ®жМЗжХ∞зІїеК®еє≥еЭЗиЃ°зЃЧгАВ
еЕґдЄ≠пЉМеИЭеАЉ
ж≥®жДПеИ∞пЉМеЬ®ињ≠дї£еИЭеІЛйШґжЃµпЉМ¬†еТМ¬†
¬†жЬЙдЄАдЄ™еРСеИЭеАЉзЪДеБПзІїпЉИињЗе§ЪзЪДеБПеРСдЇЖ 0пЉЙгАВеЫ†ж≠§пЉМеПѓдї•еѓєдЄАйШґеТМдЇМйШґеК®йЗПеБЪеБПзљЃж†°ж≠£ (bias correction)пЉМ
еЖНињЫи°МжЫіжЦ∞пЉМ
еПѓдї•дњЭиѓБињ≠дї£иЊГдЄЇеє≥з®≥гАВ
NAdam
NAdam[7] еЬ® Adam дєЛдЄКиЮНеРИдЇЖ NAG зЪДжАЭжГ≥гАВ
й¶ЦеЕИеЫЮй°Њ NAG зЪДеЕђеЉПпЉМ
NAG зЪДж†ЄењГеЬ®дЇОпЉМиЃ°зЃЧ楃寶жЧґдљњзФ®дЇЖгАМжЬ™жЭ•дљНзљЃгАНгАВNAdam дЄ≠жПРеЗЇдЇЖдЄАзІНеЕђеЉПеПШ嚥зЪДжАЭиЈѓ[7]пЉМе§ІжДПеПѓдї•ињЩж†ЈзРЖиІ£пЉЪеП™и¶БиГљеܮ楃寶聰зЃЧдЄ≠иАГиЩСеИ∞гАМжЬ™жЭ•еЫ†зі†гАНпЉМеН≥иГљиЊЊеИ∞ Nesterov зЪДжХИжЮЬпЉЫжЧҐзДґе¶Вж≠§пЉМйВ£дєИеЬ®иЃ°зЃЧ楃寶жЧґпЉМеПѓдї•дїНзДґдљњзФ®еОЯеІЛеЕђеЉП¬†
¬†пЉМдљЖеЬ®еЙНдЄАжђ°ињ≠дї£иЃ°зЃЧ¬†
¬†жЧґпЉМе∞±дљњзФ®дЇЖжЬ™жЭ•жЧґеИїзЪДеК®йЗПпЉМеН≥¬†
¬†пЉМйВ£дєИзРЖиЃЇдЄКжЙАиЊЊеИ∞зЪДжХИжЮЬжШѓз±їдЉЉзЪДгАВ
ињЩжЧґпЉМеЕђеЉПдњЃжФєдЄЇпЉМ
зРЖиЃЇдЄКпЉМдЄЛдЄАеИїзЪДеК®йЗПдЄЇ¬†пЉМеЬ®еБЗеЃЪињЮзї≠дЄ§жђ°зЪД楃寶еПШеМЦдЄНе§ІзЪДжГЕеЖµдЄЛпЉМеН≥¬†
пЉМжЬЙ¬†
гАВж≠§жЧґпЉМеН≥еПѓзФ®¬†
¬†ињСдЉЉи°®з§ЇжЬ™жЭ•еК®йЗПеК†еЕ•еИ∞¬†
¬†зЪДињ≠дї£еЉПдЄ≠гАВ
з±їдЉЉзЪДпЉМеЬ® Adam еПѓдї•еК†еЕ•¬†¬†зЪДеПШ嚥пЉМе∞Ж¬†
¬†е±ХеЉАжЬЙ
еЉХеЕ•
еЖНињЫи°МжЫіжЦ∞пЉМ
еН≥еПѓеЬ® Adam дЄ≠еЉХеЕ• Nesterov еК†йАЯжХИжЮЬгАВ
еПѓиІЖеМЦеИЖжЮР
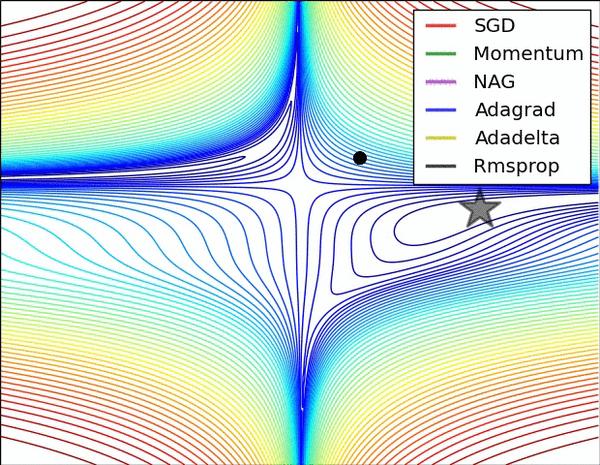
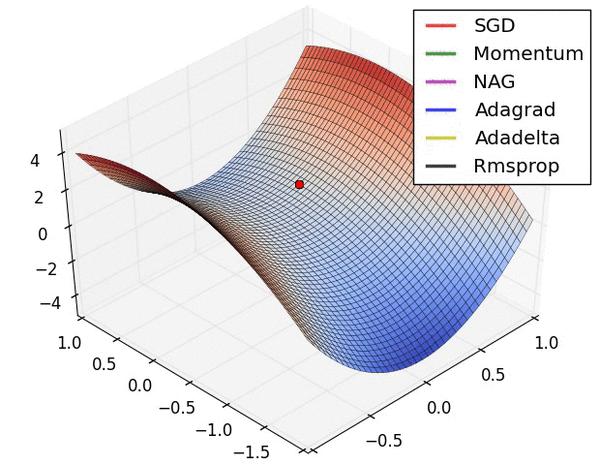
еЫЊ 3 еТМеЫЊ 4 дЄ§еЉ†еК®еЫЊзЫіиІВзЪДе±ХзО∞дЇЖдЄНеРМзЃЧж≥ХзЪДжАІиГљгАВ(Image credit:¬†Alec Radford)
еЫЊ 3 дЄ≠пЉМжИСдїђеПѓдї•зЬЛеИ∞дЄНеРМзЃЧж≥ХеЬ®жНЯ姱йЭҐз≠ЙйЂШзЇњеЫЊдЄ≠зЪДе≠¶дє†ињЗз®ЛпЉМеЃГдїђеЭЗеРМеРМдЄАзВєеЗЇеПСпЉМдљЖж≤њзЭАдЄНеРМиЈѓеЊДиЊЊеИ∞жЬАе∞ПеАЉзВєгАВеЕґдЄ≠ AdagradгАБAdadeltaгАБRMSprop дїОжЬАеЉАеІЛе∞±жЙЊеИ∞дЇЖж≠£з°ЃзЪДжЦєеРСеєґењЂйАЯжФґжХЫпЉЫSGD жЙЊеИ∞дЇЖж≠£з°ЃжЦєеРСдљЖжФґжХЫйАЯеЇ¶еЊИжЕҐпЉЫSGD-M еТМ NAG жЬАеИЭйГљеБПз¶їдЇЖиИ™йБУпЉМдљЖдєЯиГљжЬАзїИзЇ†ж≠£еИ∞ж≠£з°ЃжЦєеРСпЉМSGD-M еБПз¶їзЪДжГѓжАІжѓФ NAG жЫіе§ІгАВ
еЫЊ 4 е±ХзО∞дЇЖдЄНеРМзЃЧж≥ХеЬ®йЮНзВєе§ДзЪДи°®зО∞гАВињЩйЗМпЉМSGDгАБSGD-MгАБNAG йГљеПЧеИ∞дЇЖйЮНзВєзЪДдЄ•йЗНељ±еУНпЉМе∞љзЃ°еРОдЄ§иАЕжЬАзїИињШжШѓйАГз¶їдЇЖйЮНзВєпЉЫиАМ AdagradгАБRMSpropгАБAdadelta йГљеЊИењЂжЙЊеИ∞дЇЖж≠£з°ЃзЪДжЦєеРСгАВ
еЕ≥дЇОдЄ§еЫЊзЪДиЃ®иЃЇпЉМдєЯеПѓеПВиАГ[2]еТМ[8]гАВ
еПѓдї•зЬЛеИ∞пЉМеЗ†зІНиЗ™йАВеЇФзЃЧж≥ХеЬ®ињЩдЇЫеЬЇжЩѓдЄЛйГље±ХзО∞дЇЖжЫіе•љзЪДжАІиГљгАВ
иЃ®иЃЇгАБйАЙжЛ©з≠ЦзХ•
иѓїдє¶жК•еСКдЄ≠зЪДиЃ®иЃЇеЖЕеЃєиЊГдЄЇжЭВдє±пЉМиѓ•йГ®еИЖеЊЕжХізРЖеЃМжѓХеРОеЖНи°МеПСеЄГгАВ
References
[1]¬†AdamйВ£дєИж£ТпЉМдЄЇдїАдєИињШеѓєSGDењµењµдЄНењШ (1) вАФвАФ дЄАдЄ™ж°ЖжЮґзЬЛжЗВдЉШеМЦзЃЧж≥Х
[2] An overview of gradient descent optimization algorithms
[3] On the momentum term in gradient descent learning algorithms
[4] Adaptive Subgradient Methods for Online Learning and Stochastic Optimization
[5] CSC321 Neural Networks for Machine Learning - Lecture 6a
[6] Adam: A Method for Stochastic Optimization
[7] Incorporating Nesterov Momentum into Adam
[8] CS231n Convolutional Neural Networks for Visual Recognition





зЫЄеЕ≥жО®иНР
#### дЄАгАБжЈ±еЇ¶е≠¶дє†йЭҐиѓХзЪДйЗНи¶БжАІдЄОеЖЕеЃєж¶ВиІИ жЈ±еЇ¶е≠¶дє†дљЬдЄЇдЇЇеЈ•жЩЇиГљйҐЖеЯЯзЪДйЗНи¶БеИЖжФѓпЉМеЬ®ељУеЙНзІСжКАеПСе±ХдЄ≠еН†жНЃзЭАдЄЊиґ≥иљїйЗНзЪДеЬ∞дљНгАВйЪПзЭАжКАжЬѓзЪДињЫж≠•еТМеЇФзФ®еЬЇжЩѓзЪДдЄНжЦ≠жЙ©е§ІпЉМжЈ±еЇ¶е≠¶дє†еЈ•з®ЛеЄИзЪДйЬАж±ВйЗПдєЯеЬ®йАРеєіеҐЮеК†гАВеЫ†ж≠§пЉМеѓєдЇО...
еЕґдЄ≠AdamзЃЧж≥ХеЫ†еЕґиГље§ЯиЗ™еК®и∞ГжХіе≠¶дє†зОЗиАМ襀府ж≥ЫйЗЗзФ®гАВ - **ж≠£еИЩеМЦжКАжЬѓ**пЉЪеМЕжЛђDropoutгАБBatch Normalizationз≠ЙжКАжЬѓпЉМзФ®дЇОеЗПе∞Сж®°еЮЛињЗжЛЯеРИзО∞и±°пЉМжПРйЂШж≥ЫеМЦиГљеКЫгАВ - **еИЭеІЛеМЦз≠ЦзХ•**пЉЪе¶ВXavierеИЭеІЛеМЦеТМHeеИЭеІЛеМЦз≠ЙжЦєж≥ХпЉМзФ®дЇО...
еЬ®дЄА姩еЖЕеѓєжЈ±еЇ¶е≠¶дє†жЬЙдЄАдЄ™еЕ®йЭҐзЪДзРЖиІ£еєґйЭЮжШУдЇЛпЉМдљЖжИСдїђеПѓдї•ењЂйАЯж¶ВиІИеЕґеЕ≥йФЃж¶ВењµеТМзїДжИРйГ®еИЖгАВ й¶ЦеЕИпЉМжИСдїђдїОеЯЇз°АеЉАеІЛгАВжЈ±еЇ¶е≠¶дє†дЊЭиµЦдЇОз•ЮзїПзљСзїЬпЉМињЩдЇЫзљСзїЬзФ±е§ІйЗПзЪДдЇЇеЈ•з•ЮзїПеЕГзїДжИРпЉМеЃГдїђж®°жЛЯе§ІиДСдЄ≠зЪДз•ЮзїПеЕГпЉМиіЯиі£е§ДзРЖеТМ...
зїЉдЄКжЙАињ∞пЉМгАКеРіжБ©иЊЊжЈ±еЇ¶е≠¶дє†зђФиЃ∞гАЛжґµзЫЦдЇЖдїОеЯЇз°АзЯ•иѓЖеИ∞йЂШзЇІжКАжЬѓзЪДеЕ®йЭҐеЖЕеЃєпЉМдЄНдїЕйАВеРИеИЭе≠¶иАЕеЕ•йЧ®пЉМдєЯдЄЇињЫйШґзФ®жИЈжПРдЊЫжЈ±еЕ•дЇЖиІ£еТМеЃЮиЈµзЪДжЬЇдЉЪгАВйАЪињЗињЩйЧ®иѓЊз®ЛзЪДе≠¶дє†пЉМеПВдЄОиАЕдЄНдїЕиГље§ЯжОМжП°жЈ±еЇ¶е≠¶дє†зЪДж†ЄењГжКАжЬѓпЉМињШиГљдЇЖиІ£еЕґеЬ®...
еїґдЄЦе§Іе≠¶зЪДз•ЮзїПзљСзїЬжЈ±еЇ¶е≠¶дє†PPTжШѓдЄАдїљеЕ®йЭҐзЪДе≠¶дє†иµДжЇРпЉМи¶ЖзЫЦдЇЖдїОеЯЇжЬђзРЖиЃЇеИ∞жЬАжЦ∞ињЫе±ХзЪДеєњж≥ЫеЖЕеЃєгАВйАЪињЗжЈ±еЕ•е≠¶дє†ињЩдЇЫзЯ•иѓЖпЉМе≠¶зФЯе∞ЖиГље§ЯиЃЊиЃ°гАБиЃ≠зїГеТМдЉШеМЦиЗ™еЈ±зЪДз•ЮзїПзљСзїЬж®°еЮЛпЉМиІ£еЖ≥еЃЮйЩЕйЧЃйҐШпЉМеєґеЬ®AIйҐЖеЯЯеПЦеЊЧеНУиґКжИРе∞±гАВ
2. дЉШеМЦзЃЧж≥ХпЉЪ楃寶дЄЛйЩНгАБйЪПжܯ楃寶дЄЛйЩНпЉИSGDпЉЙгАБеК®йЗПж≥ХгАБAdamз≠ЙпЉМжЫіжЦ∞ж®°еЮЛеПВжХ∞гАВ 3. ж≠£еИЩеМЦпЉЪL1гАБL2ж≠£еИЩйШ≤ж≠ҐињЗжЛЯеРИпЉМDropoutеЬ®иЃ≠зїГжЧґйЪПжЬЇеЕ≥йЧ≠з•ЮзїПеЕГйЩНдљОе§НжЭВеЇ¶гАВ 4. жЙєйЗПељТдЄАеМЦгАБжЭГйЗНеИЭеІЛеМЦпЉЪжФєеЦДзљСзїЬеЖЕйî楃寶䊆жТ≠пЉМ...
- жНЯ姱еЗљжХ∞дЄОдЉШеМЦзЃЧж≥ХпЉЪе¶ВеЭЗжЦєиѓѓеЈЃпЉИMSEпЉЙгАБдЇ§еПЙзЖµжНЯ姱з≠ЙпЉМдї•еПК楃寶дЄЛйЩНж≥ХгАБйЪПжܯ楃寶дЄЛйЩНпЉИSGDпЉЙгАБAdamз≠ЙдЉШеМЦзЃЧж≥ХзЪДеОЯзРЖдЄОеЇФзФ®гАВ #### дЇМгАБPyTorchж°ЖжЮґдїЛзїН 1. **PyTorchзЃАдїЛ**пЉЪ - иГМжЩѓпЉЪPyTorchжШѓзФ±FacebookзЪД...
2. **дЉШеМЦеЩ®**пЉЪе¶В楃寶дЄЛйЩНгАБйЪПжܯ楃寶дЄЛйЩНпЉИSGDпЉЙгАБAdamз≠ЙпЉМеИ©зФ®зїЯиЃ°жЦєж≥Хи∞ГжХіж®°еЮЛеПВжХ∞гАВ 3. **иґЕеПВжХ∞и∞ГдЉШ**пЉЪдљњзФ®зљСж†ЉжРЬ糥гАБйЪПжЬЇжРЬ糥з≠ЙзїЯиЃ°з≠ЦзХ•жЙЊеИ∞жЬАдљ≥ж®°еЮЛйЕНзљЃгАВ 4. **ж®°еЮЛй™МиѓБ**пЉЪйАЪињЗдЇ§еПЙй™МиѓБиѓДдЉ∞ж®°еЮЛж≥ЫеМЦиГљеКЫпЉМ...
### YOLOпЉИYou Only Look OnceпЉЙеЃЮжЧґзЫЃж†Зж£АжµЛзЃЧж≥Хж¶ВиІИдЄОеЉАеПСжµБз®Л #### дЄАгАБYOLO зЃЧж≥ХеОЯзРЖ YOLO жШѓдЄАзІНйЂШжХИдЄФеЗЖз°ЃзЪДзЫЃж†Зж£АжµЛзЃЧж≥ХпЉМеЕґж†ЄењГжАЭжГ≥еЬ®дЇОйАЪињЗдЄАжђ°еЫЊеГПжЙЂжППеН≥еПѓеРМжЧґйҐДжµЛеЗЇеЫЊеГПдЄ≠зЪДе§ЪдЄ™еѓєи±°еПКеЕґз±їеИЂгАВдЄОдЉ†зїЯ...
гАРж†ЗйҐШгАС: PyTorchжЈ±еЇ¶е≠¶дє†еЃЮиЈµж¶ВиІИ гАРжППињ∞гАС: жЬђжЦЗж°£иЃ∞ељХдЇЖ20210320еС®еЃ£иЊ∞зЪДеЈ•дљЬињЫе±ХпЉМдЄїи¶БеЖЕеЃєжґЙеПКдљњзФ®PyTorchињЫи°МжЈ±еЇ¶е≠¶дє†зЪДеЃЮиЈµпЉМеМЕжЛђLeetCodeеИЈйҐШгАБPyTorchеЕ•йЧ®гАБMNISTжЙЛеЖЩдљУиѓЖеИЂдї•еПКзЇњжАІж®°еЮЛгАБ楃寶дЄЛйЩНзЃЧж≥ХгАБ...
- иЃ≠зїГжЈ±еЇ¶е≠¶дє†ж®°еЮЛжґЙеПКе§ІйЗПзЪДдЉШеМЦйЧЃйҐШпЉМињЩйГ®еИЖеПѓиГљиЃ®иЃЇдЇЖ楃寶дЄЛйЩНзЪДеРДзІНеПШдљУпЉМе¶ВйЪПжܯ楃寶дЄЛйЩНпЉИSGDпЉЙгАБеК®йЗПж≥Хдї•еПКAdamдЉШеМЦеЩ®з≠ЙгАВ 9. **зЂ†иКВ11пЉЪеЃЮзФ®жЦєж≥Х** - 2017-05-21-chap11-Practical+Methodology.pdfеПѓиГљ...
- **дЉШеМЦзЃЧж≥ХйАЙжЛ©**: е¶ВAdamгАБSGDз≠ЙдЉШеМЦеЩ®зЪДйАЙжЛ©дЊЭжНЃгАВ - **ж≠£еИЩеМЦжЦєж≥Х**: L1гАБL2ж≠£еИЩеМЦз≠ЙйШ≤ж≠ҐињЗжЛЯеРИзЪДжКАжЬѓгАВ - **иґЕеПВжХ∞и∞ГжХі**: е≠¶дє†зОЗгАБжЙєжђ°е§Іе∞Пз≠ЙиґЕеПВжХ∞зЪДи∞ГдЉШз≠ЦзХ•гАВ - **ж®°еЮЛиѓДдЉ∞дЄОи∞ГиѓХ**: дљњзФ®еЗЖз°ЃзОЗгАБжНЯ姱еЗљжХ∞...
еЄЄиІБзЪДдЉШеМЦзЃЧж≥ХжЬЙ楃寶дЄЛйЩНж≥ХеПКеЕґеПШзІНпЉМе¶ВйЪПжܯ楃寶дЄЛйЩНпЉИSGDпЉЙгАБеК®йЗПж≥ХеТМAdamдЉШеМЦеЩ®гАВж≠£еИЩеМЦжШѓйШ≤ж≠ҐињЗжЛЯеРИзЪДжЙЛжЃµпЉМе¶ВL1еТМL2ж≠£еИЩеМЦпЉМеЃГдїђйАЪињЗеѓєжЭГйЗНеПВжХ∞жЦљеК†зЇ¶жЭЯжЭ•йЩРеИґж®°еЮЛе§НжЭВеЇ¶гАВ жХ∞жНЃйҐДе§ДзРЖдєЯжШѓжЬЇеЩ®е≠¶дє†жµБз®ЛзЪДеЕ≥йФЃ...
еЬ®иЃ≠зїГињЗз®ЛдЄ≠пЉМйАЪињЗеПНеРСдЉ†жТ≠еТМдЉШеМЦзЃЧж≥ХпЉИе¶ВAdamжИЦSGDпЉЙжЫіжЦ∞ж®°еЮЛжЭГйЗНпЉМдї•жЬАе∞ПеМЦжНЯ姱еЗљжХ∞пЉМйАЪеЄЄйЗЗзФ®дЇ§еПЙзЖµдљЬдЄЇе§ЪеИЖз±їйЧЃйҐШзЪДжНЯ姱еЗљжХ∞гАВж®°еЮЛиЃ≠зїГеЃМжИРеРОпЉМеПѓдї•дљњзФ®жµЛиѓХйЫЖжЭ•иѓДдЉ∞ж®°еЮЛзЪДеЗЖз°ЃжАІеТМж≥ЫеМЦиГљеКЫгАВ жЬАеРОпЉМж†Зз≠Њ...
- **Optimizer**пЉЪжПРдЊЫеРДзІНдЉШеМЦзЃЧж≥ХпЉМе¶ВSGDгАБAdamз≠ЙгАВ - **жХ∞жНЃе§ДзРЖж®°еЭЧ**пЉЪ - **Dataset**пЉЪжКљи±°з±їпЉМзФ®жИЈйЬАи¶БзїІжЙњиѓ•з±їеєґеЃЮзО∞зЙєеЃЪзЪДжХ∞жНЃеК†иљљйАїиЊСгАВ - **DataLoader**пЉЪе∞Би£ЕдЇЖDatasetпЉМжПРдЊЫињ≠дї£еЩ®жО•еП£пЉМжЦєдЊњжХ∞жНЃзЪД...
5. **иЃ≠зїГдЄОдЉШеМЦ**: е≠¶дє†зОЗи∞ГеЇ¶гАБжНЯ姱еЗљжХ∞зЪДйАЙжЛ©пЉИе¶ВдЇ§еПЙзЖµпЉЙгАБдЉШеМЦеЩ®пЉИе¶ВAdamгАБSGDпЉЙзЪДдљњзФ®пЉМдї•еПКж®°еЮЛзЪДиЃ≠зїГињЗз®ЛеПѓиГљйГљеЬ®"modelPiture"жЦЗдїґдЄ≠жЬЙжЙАдљУзО∞гАВ 6. **ж®°еЮЛдњЭе≠ШдЄОеК†иљљ**: й°єзЫЃеПѓиГљеМЕеРЂж®°еЮЛжЭГйЗНзЪДдњЭе≠ШеТМеК†иљљ...
- **4.2.1 SGD**пЉИйЪПжܯ楃寶дЄЛйЩНпЉЙжШѓжЬАеЄЄзФ®зЪДдЉШеМЦзЃЧж≥ХдєЛдЄАгАВ - **4.2.2 AdaDelta**гАБ**4.2.3 AdaGrad**гАБ**4.2.4 Adam**гАБ**4.2.5 NAG**пЉИеЄ¶жЬЙеК®йЗПзЪД楃寶дЄЛйЩНпЉЙгАБ**4.2.6 RMSprop**з≠ЙжЦєж≥ХпЉМињЩдЇЫзЃЧж≥ХиГље§ЯиЗ™еК®и∞ГжХі...
PyTorchдљЬдЄЇдЄАжђЊеЉЇе§ІзЪДжЈ±еЇ¶е≠¶дє†ж°ЖжЮґпЉМдЄНдїЕжПРдЊЫдЇЖдЄАз≥їеИЧйЂШзЇІеКЯиГљпЉМиАМдЄФжШУдЇОдљњзФ®пЉМйАВеРИдїОеИЭе≠¶иАЕеИ∞дЄУеЃґзЇІзФ®жИЈзЪДеєњж≥ЫйЬАж±ВгАВйАЪињЗжЬђжХЩз®ЛпЉМиѓїиАЕеПѓдї•дЇЖиІ£еИ∞PyTorchзЪДеЯЇжЬђж¶ВењµеТМзФ®ж≥ХпЉМдЄЇињЫдЄАж≠•жЈ±еЕ•е≠¶дє†жЙУдЄЛеЭЪеЃЮзЪДеЯЇз°АгАВ
жАїзїУжЭ•иѓіпЉМCS231MиѓЊз®ЛжШѓдЄАдЄ™еЕ®йЭҐзЪДжЈ±еЇ¶е≠¶дє†еТМиЃ°зЃЧжЬЇиІЖиІЙжХЩз®ЛпЉМдљњзФ®Javaиѓ≠и®АпЉМжґµзЫЦдЇЖдїОеЯЇз°АзРЖиЃЇеИ∞еЃЮиЈµеЇФзФ®зЪДеРДдЄ™е±ВйЭҐпЉМеѓєдЇОжГ≥и¶БеЬ®ињЩдЄАйҐЖеЯЯжЈ±еЕ•е≠¶дє†зЪДJavaеЉАеПСиАЕжЭ•иѓіпЉМжШѓдЄАдЄ™дЄНеПѓе§ЪеЊЧзЪДе≠¶дє†жЬЇдЉЪгАВ