白化(预处理步骤)【转】
介绍
我们已经了解了如何使用PCA降低数据维度。在一些算法中还需要一个与之相关的预处理步骤,这个预处理过程称为白化。举例来说,假设训练数据是图像,由于图像中相邻像素之间具有很强的相关性,所以用于训练时输入是冗余的。白化的目的就是降低输入的冗余性;更正式的说,我们希望通过白化过程使得学习算法的输入具有如下性质:(i)特征之间相关性较低;(ii)所有特征具有相同的方差。
2D的例子
下面我们先用前文的2D例子描述白化的主要思想,然后分别介绍如何将白化与平滑和PCA相结合。
如何消除特征之间的相关性?在前文计算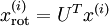 时实际上已经消除了输入特征
时实际上已经消除了输入特征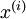 之间的相关性。得到的新特征
之间的相关性。得到的新特征 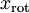 的分布如下图所示:
的分布如下图所示:
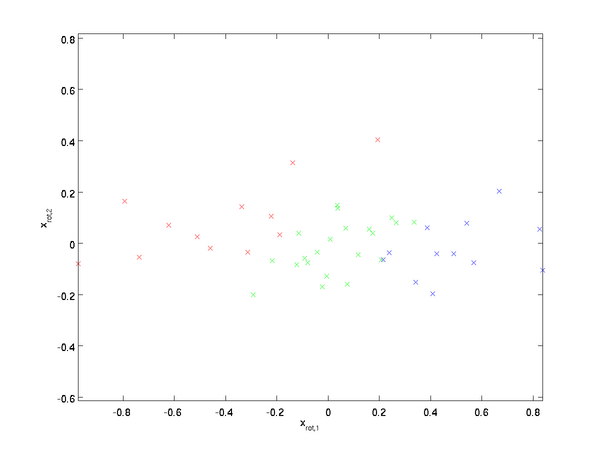
这个数据的协方差矩阵如下:
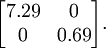
(注:严格地讲,这部分许多关于“协方差”的陈述仅当数据均值为0时成立。下文的论述都隐式地假定这一条件成立,不过即使数据均值不为0,下文的说法仍然成立,所以你无需担心这个。)
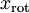 协方差矩阵对角元素的值为
协方差矩阵对角元素的值为 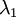 和
和 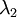 绝非偶然。并且非对角元素值为0; 因此,
绝非偶然。并且非对角元素值为0; 因此, 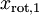 和
和 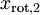 是不相关的, 满足我们对白化结果的第一个要求 (特征间相关性降低)。
是不相关的, 满足我们对白化结果的第一个要求 (特征间相关性降低)。
为了使每个输入特征具有单位方差,我们可以直接使用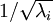 作为缩放因子来缩放每个特征
作为缩放因子来缩放每个特征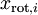 。具体地,我们定义白化后的数据
。具体地,我们定义白化后的数据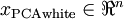 如下:
如下: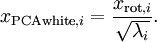
绘制出 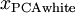 ,我们得到:
,我们得到:
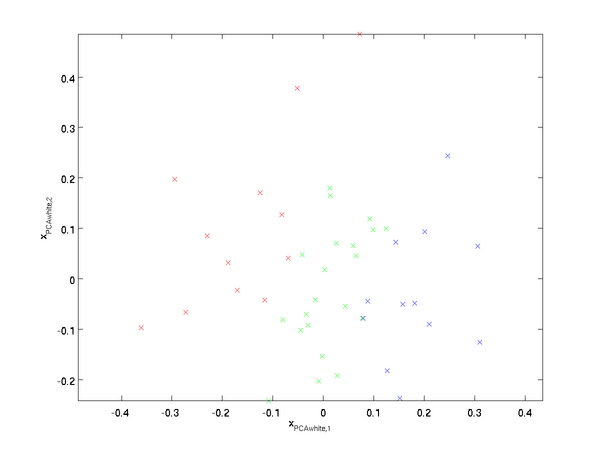
这些数据现在的协方差矩阵为单位矩阵I。我们说,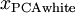 是数据经过PCA白化后的版本:
是数据经过PCA白化后的版本: 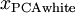 中不同的特征之间不相关并且具有单位方差。
中不同的特征之间不相关并且具有单位方差。
白化与降维相结合:如果你想要得到经过白化后的数据,并且比初始输入维数更低,可以仅保留 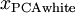 中前
中前  个成分。当我们把PCA和正则化结合起来时(在稍后讨论),
个成分。当我们把PCA和正则化结合起来时(在稍后讨论),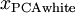 中最后的少量成分将总是接近于0,因而舍弃这些成分不会带来很大的问题。
中最后的少量成分将总是接近于0,因而舍弃这些成分不会带来很大的问题。
ZCA白化
最后要说明的是,是数据的协方差矩阵变为单位矩阵I的方式并不唯一。具体地,如果R是任意正交矩阵,即满足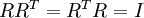 (说它正交不太严格,R可以是旋转或反射矩阵),那么
(说它正交不太严格,R可以是旋转或反射矩阵),那么
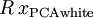 仍然具有单位协方差。在ZCA白化中,令
仍然具有单位协方差。在ZCA白化中,令 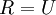 。我们定义ZCA白化的结果为:
。我们定义ZCA白化的结果为: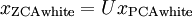
绘制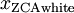 ,得到:
,得到:
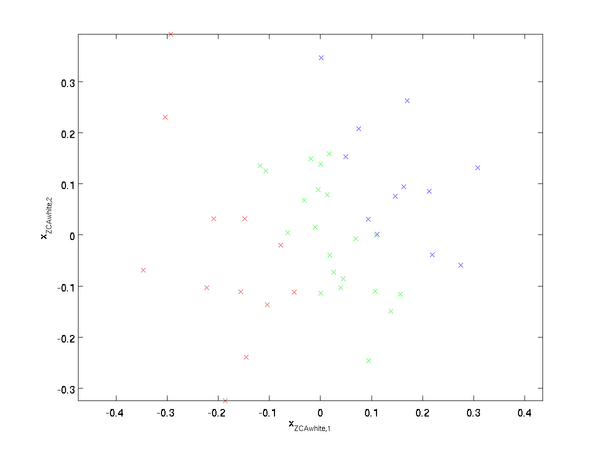
可以证明,对所有可能的R,这种旋转式的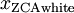 尽可能地接近原始输入数据x。当使用ZCA白化时(不同于PCA白化),我们通常保留数据的全部n个维度,不尝试去降低它的维数。
尽可能地接近原始输入数据x。当使用ZCA白化时(不同于PCA白化),我们通常保留数据的全部n个维度,不尝试去降低它的维数。
正则化
实践中需要实现PCA白化或ZCA白化时,有时一些特征值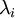 在数值上接近于0,这样在缩放步骤时我们除以
在数值上接近于0,这样在缩放步骤时我们除以 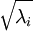 将导致除以一个接近0的值;这可能会导致数据上溢(赋为最大值)或造成数值不稳定。因而在实践中,我们使用少量的正则化实现这个缩放过程,即在取平方根和倒数之前给特征值加上一个很小的常数
将导致除以一个接近0的值;这可能会导致数据上溢(赋为最大值)或造成数值不稳定。因而在实践中,我们使用少量的正则化实现这个缩放过程,即在取平方根和倒数之前给特征值加上一个很小的常数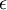 :
:
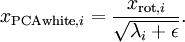
当  在区间
在区间 ![\textstyle [-1,1]](http://deeplearning.stanford.edu/wiki/images/math/8/5/a/85a1c5a07f21a9eebbfb1dca380f8d38.png) 上时, 一般取值为
上时, 一般取值为 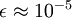 。
。
对图像来说,这里加上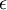 ,对输入图像也有一些平滑(或低通滤波)的作用。这样处理还能消除在图像的像素信息获取过程中产生的噪声,改善学习到的特征。
,对输入图像也有一些平滑(或低通滤波)的作用。这样处理还能消除在图像的像素信息获取过程中产生的噪声,改善学习到的特征。
ZCA白化是一种数据预处理方法,它将数据从  映射到
映射到 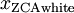 。
。
事实证明这也是一种生物眼睛(视网膜)处理图像的粗糙模型。具体而言,当你的眼睛感知图像时,由于一幅图像中相邻的部分在亮度上十分相关,大多数临近的“像素”在眼中被感知为相近的值。因此,如果人眼需要分别传输每个像素值(通过视觉神经)到大脑中,会非常不划算。取而代之的是,视网膜进行一个与ZCA中相似的去相关操作(这是由视网膜上的ON-型和OFF-型光感受器细胞将光信号转变为神经信号完成的)。由此得到对输入图像的更低冗余的表示,并将它传输到大脑。





相关推荐
在这一领域,白化预处理是常用于改善信号特性,便于后续分离操作的重要步骤。自然梯度算法则是一种优化方法,它在BSS问题中扮演了关键角色。 首先,我们来理解一下白化预处理。白化(Whitening)是将多维数据转换成...
1. 零均值化:这是最基础的数据预处理步骤,通过减去每个特征的均值,使数据集的每个特征具有零均值。 2. 方差标准化:也称为单位方差标准化,通过除以每个特征的标准差,使得数据的每个维度都具有单位方差。 3. ...
总而言之,预白化处理作为一种在频域中对信号进行预处理的手段,通过将原始信号转换为功率谱密度均匀分布的白色信号,大大简化了信号的频域特性,从而为后续的特征提取、故障检测等分析步骤提供了便利。而随着C#等...
而"白化"则是预处理步骤,它将数据转换为一组标准正态分布,以便于后续的ICA分析。 首先,让我们深入理解独立成分分析(ICA)。ICA的目标是从观测到的混合信号中分离出互不相关的原始信号。这些原始信号通常无法直接...
白化(Whitening)是预处理步骤,其目的是将原始数据转换为具有单位方差且各分量间互不相关的形式。这有助于减少后续分析的复杂性,尤其是在ICA中,可以简化源信号的分离过程。白化的数学操作通常涉及对数据进行标准...
这样的组合预处理步骤有助于提升某些机器学习算法,如支持向量机(SVM)、神经网络等的性能,因为它们可能对输入数据的尺度和相关性敏感。 总的来说,"数据预处理的文件"中的whitenv.m和remmean.m是实现数据预处理...
在信号处理领域,白化是一种重要的预处理技术,主要用于改变信号的统计特性,使其各分量之间变得相互独立且具有相同的方差。标题中的“white_matlab_信号处理_白化matlab_white_白化_”揭示了我们将讨论的是如何在...
白化则是另一种数据预处理技术,它旨在使数据在各个方向上的方差为1,并且各方向之间互不相关,即协方差矩阵为单位矩阵。白化通常在PCA之后进行,通过进一步的标准化步骤,使得变换后的数据具有单位范数(各分量方差...
在MATLAB中实现PCA,通常包括数据预处理、计算协方差矩阵或中心化数据、特征值分解以及选择主成分等步骤。 白化操作是PCA的后续处理,它进一步标准化数据,使得每个特征在新的坐标系下具有相同的方差且相互独立。...
总结,基于负熵最大化的FastICA算法是解决复杂数据混合问题的有效工具,其核心是通过最大化负熵来寻找非高斯分布的独立分量,而白化预处理则极大地简化了问题,提高了算法的效率。这种算法在多个领域都有广泛的应用...
`remmean`函数则是用来去除数据的均值,这是一个预处理步骤,因为在ICA中,通常要求输入数据是非中心化的。去均值是为了消除信号的平均值,确保后续分析不受全局偏置的影响。 `whiten`函数执行白化处理,这一步是将...
- **白化过程**:在FastICA之前,通常先进行预处理步骤——白化,即将数据转换为零均值、单位方差且各维度之间协方差为零的状态,这有助于简化后续的计算。 2. **FastICA的C实现** 在C语言中实现FastICA,首先...
- 在实际应用中,FastICA通常结合白化预处理步骤,先将数据进行预处理,使其接近高斯分布,以便更好地突出非高斯特征。 3. **FastICA的步骤**: - 数据预处理:对数据进行归一化和白化,减少噪声影响,使数据接近...
噪声白化是一种预处理步骤,用于减小噪声的非平坦功率谱密度,使其更接近白噪声,从而提高后续处理的效率。频谱重排则是一种策略,通过对时频谱进行重新排列,以更好地揭示语音信号的结构,降低噪声影响。 WSRRPCA...
数据矩阵的白化是一种常用的预处理技术,在许多机器学习和数据分析任务中都有应用。它通过线性变换将原始数据转换到一个新的坐标系中,使得新坐标系下的数据具有单位协方差矩阵,即各维度之间互不相关。这种操作可以...
PCA(主成分分析)和白化是两种在数据预处理中常见的技术,尤其在深度学习领域,它们可以优化模型的训练效果和提升预测性能。PCA是一种无监督的线性降维方法,它通过找到原始数据集的主要方向(主成分)来减少数据的...
综上所述,白化变换作为一种重要的预处理技术,在图像处理、计算机视觉乃至更广泛的机器学习领域中扮演着不可或缺的角色。通过对数据进行适当的变换,不仅可以简化模型的设计,还能有效提升模型的表现能力。
1. **数据预处理**: - **去均值**:首先,需要对数据进行中心化处理,即将每个特征的均值移除,使得数据的平均值为0。在给定的代码中,`meanValue` 存储了数据的均值,然后使用`meanValue * ones(1, size(mean...