阅读目录
原文地址:http://www.cnblogs.com/jacklu/p/7753471.html
本文结合了王晓刚老师的ENGG 5202 Pattern Recognition课程内容知识,和搜集的资料和自己理解的总结。
1 概述
隐马尔可夫模型(Hidden Markov Model,HMM)是结构最简单的贝叶斯网,这是一种著名的有向图模型,主要用于时序数据建模(语音识别、自然语言处理等数据在时域有依赖性的问题)。
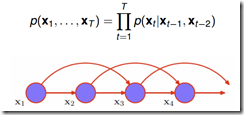
如果考虑t时刻数据依赖于0到t-1时间段的所有数据,即![]() ,在计算复杂度上是不可行的。因此Markov Model假定只依赖于最近的几个观测数据。
,在计算复杂度上是不可行的。因此Markov Model假定只依赖于最近的几个观测数据。
下面先从一个直观的例子理解HMM:
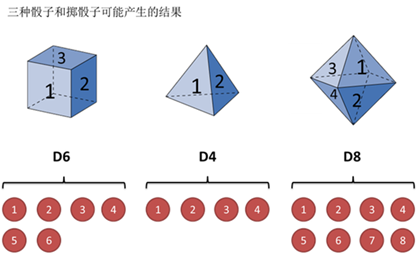
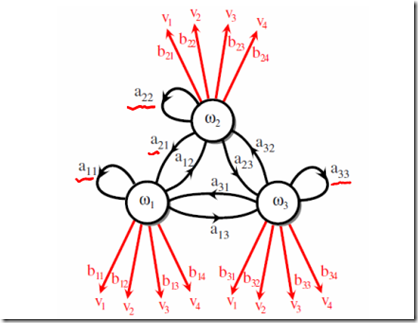
假设有三个不同的骰子(6面、4面、8面),每次先从三个骰子里选一个,每个骰子选中的概率为![]() ,如下图所示,重复上述过程,得到一串数字[1 6 3 5 2 7]。这些可观测变量组成可观测状态链。
,如下图所示,重复上述过程,得到一串数字[1 6 3 5 2 7]。这些可观测变量组成可观测状态链。
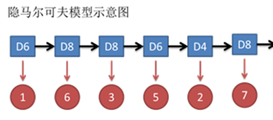
同时,在隐马尔可夫模型中还有一条由隐变量组成的隐含状态链,在本例中即骰子的序列。比如得到这串数字骰子的序列可能为[D6 D8 D8 D6 D4 D8]。
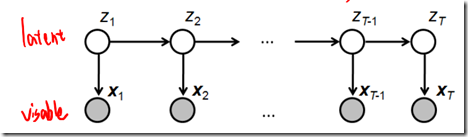
隐马尔可夫模型示意图如下所示:
图中,箭头表示变量之间的依赖关系。在任意时刻,观测变量(骰子点数)仅依赖于状态变量(哪类骰子),“观测独立性假设”。
同时,t时刻数据依赖于t-1时刻的数据。这就是1阶马尔可夫链,即系统的下一时刻的状态仅由当前状态决定不依赖以往的任何状态(无记忆性),“齐次马尔可夫性假设”。
0阶Markov Model:
1阶Markov Model:
2阶Markov Model:
1阶HMM
包含状态变量(也叫latent variable,该变量是离散的、未知的、待推断的) 和观测变量(该变量可以是离散的、也可以是连续的)
和观测变量(该变量可以是离散的、也可以是连续的) ,如下图所示:
,如下图所示:
1.2 HMM中的条件独立(在后续算法推导中非常重要)
从概率图模型上给出条件独立的式子非常简单,即遮住某一节点,被分开的路径在给定该节点时独立。
上面六个式子,前五个式子很容易从图模型中理解。最后一个式子可以将左边写成![]() 和
和 的乘积,然后再将
的乘积,然后再将 做分解。
做分解。
假定每个状态有三种取值![]() ,比如上面骰子的种类。参数如下图所示:
,比如上面骰子的种类。参数如下图所示:
观测概率(也叫emission probablity)![]() ,即时刻t、状态
,即时刻t、状态![]() 的概率
的概率
2 隐马尔可夫模型三要素
以上三个参数构成隐马尔可夫模型三要素:
3 隐马尔可夫模型的三个基本问题
(1) 给定模型![]() ,计算其产生观测序列
,计算其产生观测序列![]() 的概率
的概率![]() , 称作evaluation problem,比如:计算掷出点数163527的概率
, 称作evaluation problem,比如:计算掷出点数163527的概率
(2) 给定模型![]() 和观测序列
和观测序列![]() ,推断能够最大概率产生此观测序列的状态序列
,推断能够最大概率产生此观测序列的状态序列![]() ,即使求解
,即使求解![]() ,称作decoding problem,比如:推断掷出点数163527的骰子种类
,称作decoding problem,比如:推断掷出点数163527的骰子种类
(3) 给定观测序列![]() ,估计模型
,估计模型![]() 的参数,使计算其产生观测序列的概率
的参数,使计算其产生观测序列的概率![]() 最大,称作learning problem,比如:已知骰子有几种,不知道骰子的种类,根据多次掷出骰子的结果,反推出骰子的种类
最大,称作learning problem,比如:已知骰子有几种,不知道骰子的种类,根据多次掷出骰子的结果,反推出骰子的种类
这三个基本问题在现实应用中非常重要,例如根据观测序列推测当前时刻最有可能出现的观测值![]() ,这就是基本问题(1);
,这就是基本问题(1);
在语音识别中,观测值为语音信号,隐藏状态为文字,根据观测信号推断最有可能的状态序列,即基本问题(2);
在大多数应用中,人工指定参数模型已变得越来越不可行,如何根据训练样本学得最优参数模型,就是基本问题(3)。
4 三个基本问题的解法
基于两个条件独立假设,隐马尔可夫模型的这三个基本问题均能被高效求解。
4.1 基本问题(1)evaluation problem解法
4.1.1 直接计算法(概念上可行,计算上不可行)
通过列举所有可能的长度为T的状态序列![]() ,求各个状态序列与观测序列同时出现的联合概率
,求各个状态序列与观测序列同时出现的联合概率![]() ,然后对所有可能求和。
,然后对所有可能求和。
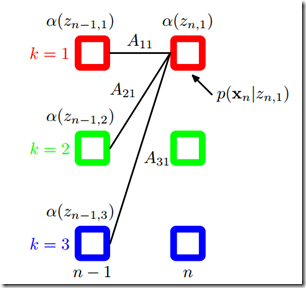
4.1.2 前向算法(t=1,一步一步向前计算)
注意求和式中有K项(Z的状态数),计算复杂度为C*C。
通过上式可知,为了得到前向概率![]() ,可以先初始化t=1时刻的概率,然后从第一个节点开始递推计算,每次递推都需要计算一次c*c的的操作,因此总的算法复杂度是
,可以先初始化t=1时刻的概率,然后从第一个节点开始递推计算,每次递推都需要计算一次c*c的的操作,因此总的算法复杂度是![]() (C和K相同)
(C和K相同)
4.1.3 后向算法
推导过程:
通过上式可知,为了得到后向概率![]() ,可以先初始化t=T时刻的概率,然后从最后一个节点向前递推计算,每次递推都需要计算一次c*c的的操作,因此总的算法复杂度是
,可以先初始化t=T时刻的概率,然后从最后一个节点向前递推计算,每次递推都需要计算一次c*c的的操作,因此总的算法复杂度是![]() (C和K相同)
(C和K相同)
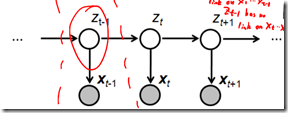
算法高效的关键是其局部计算前向概率,根据路径结构,如下图所示,每次计算直接利用前一时刻计算结果,避免重复计算,减少计算量。
给定观测序列,t时刻从某一状态,在t+1时刻转换成新的状态的后验概率![]() :
:
4.2 基本问题(2)decoding problem解法
4.2.1 近似算法
选择每一时刻最有可能出现的状态,即根据上述计算t时刻的状态后验概率![]() ,选择概率最大的状态,从而得到一个状态序列。这个方法计算简单,此方法但是不能保证整个状态序列的出现概率最大。因为可能两个相邻的状态转移概率为0,即实际上不可能发生这种状态转换。
,选择概率最大的状态,从而得到一个状态序列。这个方法计算简单,此方法但是不能保证整个状态序列的出现概率最大。因为可能两个相邻的状态转移概率为0,即实际上不可能发生这种状态转换。
4.2.2 Viterbi算法
使用动态规划求解概率最大(最优)路径。t=1时刻开始,递推地计算在时刻t状态为i的各条部分路径的最大概率,直到计算到时刻T,状态为i的各条路径的最大概率,时刻T的最大概率即为最优路径的概率,最优路径的节点也同时得到。
如果还不明白,看一下李航《统计学习方法》的186-187页的例题就能明白算法的原理。
考虑一个表格数据结构![]() ,存储着t时刻时,状态为j的能够产生观测序列
,存储着t时刻时,状态为j的能够产生观测序列![]() 的最大概率值。
的最大概率值。
t>1时
维特比算法:
维特比算法图示:
状态[3 3 3]极为概率最大路径。
4.3 基本问题(3)解法
4.3.1 监督学习方法
给定T个长度相同的(观测序列,状态序列)![]() 作为训练集,使用极大似然估计法来估计模型参数。
作为训练集,使用极大似然估计法来估计模型参数。
转移概率 ![]() 的估计:样本中t时刻处于状态i,t+1时刻转移到状态j的频数为
的估计:样本中t时刻处于状态i,t+1时刻转移到状态j的频数为![]() ,则
,则
4.3.2 Baum-Welch算法
使用EM算法得到模型参数估计式
EM算法是常用的估计参数隐变量的利器,它是一种迭代方法,基本思想是:
(1) 选择模型参数初始值;
(2) (E步)根据给定的观测数据和模型参数,求隐变量的期望;
(3) (M步)根据已得隐变量期望和观测数据,对模型参数做极大似然估计,得到新的模型参数,重复第二步。
作业题:
第一问用于理解HMM产生数据的过程,第二问用于理解维特比算法。
自己写的答案(运行结果如上图):
1 import numpy
2 import random
3
4 def random_pick(pick_list,probability_list):
5 x=random.uniform(0,1)
6 cumulative_probability=0.0
7 for item,item_probability in zip(pick_list,probability_list):
8 cumulative_probability+=item_probability
9 if x < cumulative_probability: break
10 return item
11
12 Zt=[1,2]
13 Pi=[0.6,0.4]
14 Xt=[1,2,3]
15 a1j=[0.7, 0.3]
16 a2j=[0.4, 0.6]
17 b1j=[0.1, 0.4, 0.5]
18 b2j=[0.6, 0.3, 0.1]
19 x=[-1 for n in range(10)]
20 z=[-1 for n in range(10)]
21 #for function test
22 #temp_counter = 0
23 #for i in range(100):
24 # if random_pick(Zt,Pi) == 1: temp_counter+=1
25 #print(temp_counter)
26 ##for function test
27
28 z[0] = random_pick(Zt,Pi)
29 for i in range(10):
30 if z[i] == 1:
31 x[i] = random_pick(Xt, b1j)
32 if i < 9: z[i+1] = random_pick(Zt, a1j)
33 else:
34 x[i]= random_pick(Xt, b2j)
35 if i < 9: z[i+1]= random_pick(Zt, a2j)
36 print(z)
37 print(x)
38
39 bp=[-1 for n in range(10)]
40 Fi=[[-1,-1] for n in range(10)]
41 for i in range(2):
42 if i == 0:
43 Fi[0][0]=Pi[i]*b1j[x[0]-1]
44 print('Fi00',Fi[0][0])
45 elif i == 1:
46 Fi[0][1]=Pi[i]*b2j[x[0]-1]
47 print('Fi01',Fi[0][1])
48 if Fi[0][0] < Fi[0][1]:
49 bp[0] = 1
50 else:
51 bp[0] = 0
52
53 for t in range(9):
54 for j in range(2):
55 if j == 0:
56 if bp[t] == 0:
57 Fi[t+1][j]=Fi[t][0]*a1j[0]*b1j[x[t+1]-1]
58 elif bp[t] == 1:
59 Fi[t+1][j]=Fi[t][1]*a2j[0]*b1j[x[t+1]-1]
60 if j == 1:
61 if bp[t] == 0:
62 Fi[t+1][j]=Fi[t][0]*a1j[1]*b2j[x[t+1]-1]
63 elif bp[t] == 1:
64 Fi[t+1][j]=Fi[t][1]*a2j[1]*b2j[x[t+1]-1]
65 print('Fit0',Fi[t+1][0])
66 print('Fit1',Fi[t+1][1])
67 if Fi[t+1][0] < Fi[t+1][1]:
68 bp[t+1] = 1
69 else:
70 bp[t+1] = 0
71
72 print(bp)#z=bp+1



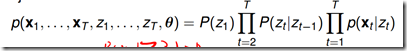
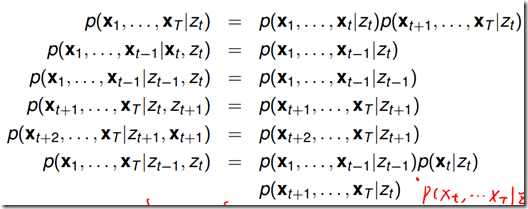
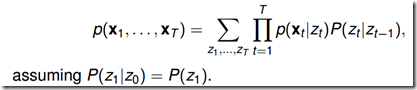

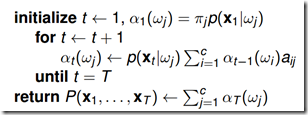
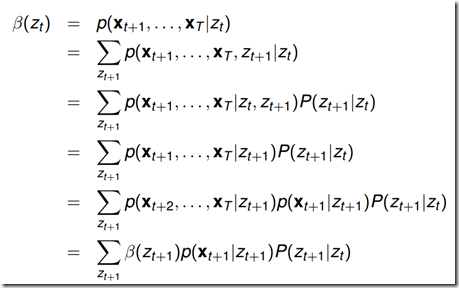
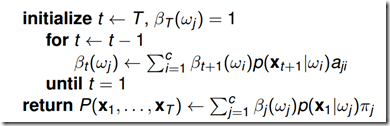
![clip_image064[7] clip_image064[7]](https://images2015.cnblogs.com/blog/718161/201612/718161-20161227131012242-518834659.jpg)

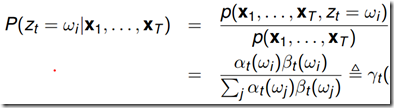
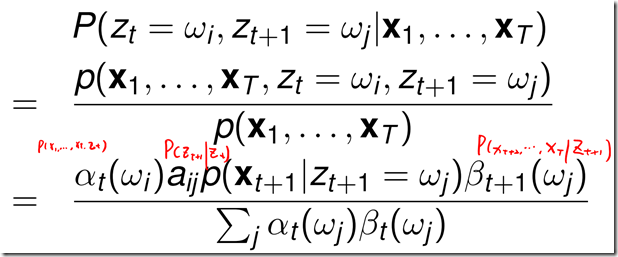
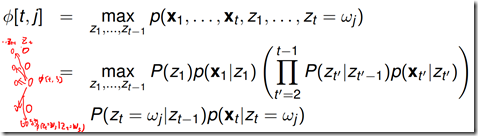
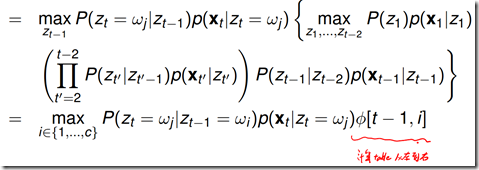

![clip_image082[4] clip_image082[4]](https://images2015.cnblogs.com/blog/718161/201612/718161-20161227131013320-1346879940.jpg)
![clip_image094[4] clip_image094[4]](https://images2015.cnblogs.com/blog/718161/201612/718161-20161227131018851-1663417510.png)








相关推荐
在“10.2 基于隐马尔可夫模型(HMM)的孤立字语音识别实验”这个压缩包中,很可能包含了完整的MATLAB代码示例,包括特征提取、模型训练和识别的脚本。通过阅读和理解这些代码,你可以深入学习和掌握HMM在孤立字语音...
预测问题通常采用维特比算法(Viterbi Algorithm),该算法是一种动态规划算法,用于找出观测序列最可能对应的隐状态序列,即分词的最优路径。 在实际应用中,为了提高分词的准确性,需要对HMM模型进行训练,从含有...
隐马尔可夫模型(HMM)是一种统计建模方法,尤其在自然语言处理和语音识别领域中广泛应用。它基于马尔可夫模型的概念,但增加了“隐藏”或不可观测的状态,这些状态通过一系列可观察的输出来表现。在HMM中,系统处于...
### 隐马尔可夫模型 (HMM) 概念与应用 #### 一、马尔可夫性 在探讨隐马尔可夫模型之前,我们先了解马尔可夫性的基本概念。马尔可夫性指的是一个过程的未来状态只依赖于当前状态,而与过去的状态无关。这一特性在很...
HMM的三个基本算法包括:前向算法(Forward Algorithm)、后向算法(Backward Algorithm)和维特比算法(Viterbi Algorithm)。前向算法计算在给定观测序列下,模型处于任意状态的概率;后向算法则计算从某一时刻...
常用的解码算法包括维特比算法(Viterbi Algorithm),它能够高效地找到最优路径。 ##### 4.3 应用实例 - **中文分词**:利用HMM对未标记的文本进行分词处理。 - **语音识别**:根据音频信号识别出对应的文本内容...
隐马尔可夫模型(Hidden Markov Model,简称HMM)是概率模型中的一种,它在统计学习方法中被广泛应用于自然语言处理、语音识别、生物信息学等领域。HMM的核心思想是假设观察序列是由一个不可见的马尔可夫过程生成的...
隐马尔可夫模型(Hidden Markov Model,简称HMM)是概率统计领域中的一个重要模型,尤其在自然语言处理、语音识别、生物信息学等多个IT领域有着广泛应用。它是一种能够处理观察序列数据的统计模型,其中的状态过程是...
隐马尔可夫模型(Hidden Markov Model,简称HMM)是概率统计领域的一种重要模型,广泛应用于自然语言处理、语音识别、生物信息学等多个领域。在本资源中,我们有MATLAB编写的HMM源代码,对于学习和理解HMM的原理以及...
隐马尔可夫模型(Hidden Markov Model,简称HMM)...总之,隐马尔可夫模型在C++中的实现涉及到概率统计、动态规划和优化算法等多个IT领域的知识,理解和掌握这些内容对于提升在相关领域的分析和解决问题能力至关重要。
总的来说,MATLAB的HMM工具箱为研究人员和工程师提供了一个强大且易用的平台,使得处理和分析基于隐马尔可夫模型的复杂问题变得更加便捷和高效。通过熟练掌握这个工具箱,用户可以深入探索HMM在各种领域的应用,并...
使用隐马尔可夫模型与维特比算法进行中文分词标注,c++编写。语料库为人民日报语料库(1998年1月至_NLP-HMM-viterbi
隐马尔可夫模型(Hidden Markov Model,简称HMM)是概率统计领域的一种重要算法,广泛应用于自然语言处理、语音识别、生物信息学等多个领域。HMM的主要特点是模型内部的状态不可观测,只能通过一系列的观测序列来...
隐马尔可夫模型(Hidden Markov Model,简称HMM)是一种统计建模方法,广泛应用于自然语言处理、语音识别、生物信息学等领域。在MATLAB中,开发HMM工具箱是为了方便研究者和工程师进行相关算法的实现与实验。本工具...
**C#编写的隐马尔可夫模型...总之,C#编写的隐马尔可夫模型分词程序通过学习和应用HMM理论,实现了对中文文本的有效分词。结合源代码和实验报告,开发者可以深入理解HMM的工作原理,并在此基础上进行二次开发和优化。
隐马尔可夫模型(HMM,Hidden Markov Model)是一种在统计学和计算机科学领域广泛应用的概率模型,尤其在自然语言处理、语音识别、生物信息学等领域占据着核心地位。这个压缩包“hmm.rar”显然包含了一些实现HMM基本...
这种算法特别适用于处理带有隐状态的马尔可夫链,即隐马尔可夫模型(Hidden Markov Model,简称HMM)。在隐马尔可夫模型中,系统的状态是不可直接观察到的,只能通过观察到的事件来间接推断系统的状态。维特比算法...
3. **两大问题**:在HMM中,我们通常关心两个问题:前向-后向算法(Forward-Backward Algorithm)用于计算给定观测序列的模型概率,以及维特比算法(Viterbi Algorithm)用于找到最可能的状态序列。 **语音识别与...