参考:http://www.cnblogs.com/pangliang/archive/2011/02/27/1966303.html
用有向图表示的概率模型也叫“贝叶斯网络”. 贝叶斯网络中的两个结点 与
与 关于结点(或结点集合)
关于结点(或结点集合) 条件独立时我们称
条件独立时我们称 “D-separates”
“D-separates” 与
与 , 写作
, 写作 . D-Separation中的D指Directed. 从图形上看, 结点集合
. D-Separation中的D指Directed. 从图形上看, 结点集合 “D-separates”结点
“D-separates”结点 与结点
与结点 是指任意一条从
是指任意一条从 到
到 的路径中都出现了以下两种情形之一:
的路径中都出现了以下两种情形之一:
- 存在样式
 或
或 , 且
, 且 ;
;
- 存在样式
 , 且
, 且 及其所有后代都不属于
及其所有后代都不属于 .
.
这几种情形的示意图:
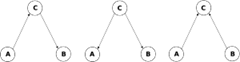
第一和第二个图中,  , 而
, 而 ; 第三个图中,
; 第三个图中,  , 而
, 而 .
.
贝叶斯球算法是判断贝叶斯网络中任意一对结点是否条件独立的一种较为直观的算法. 其思想是, 设想在贝叶斯网络中有一个按一定规则运行的球, 在给出已知结点集合 的情况下判断球能否由
的情况下判断球能否由 结点出发到达
结点出发到达 结点(或者反过来, 由
结点(或者反过来, 由 到
到 ). 如果可以, 那么判断
). 如果可以, 那么判断 ; 反之则有
; 反之则有 .
.
每一个结点可以已知(属于 )或未知(不属于
)或未知(不属于 ). 定义几个术语:
). 定义几个术语:
- 通过(pass through): 贝叶斯球从当前结点的父结点方向过来时, “通过”指当前结点允许贝叶斯球访问自己的所有子结点; 贝叶斯球从当前结点的子结点方向过来时, “通过”指当前结点允许贝叶斯球访问自己的所有父结点.
- 反弹(bounce back): 贝叶斯球从当前结点的父结点方向过来时, “反弹”指当前结点允许贝叶斯球访问自己的所有父结点; 贝叶斯球从当前结点的子结点方向过来时, “反弹”指当前结点允许贝叶斯球访问自己的所有子结点.
- 截止(block): 当前结点阻止贝叶斯球继续运动.
使用上面的术语, 贝叶斯球运行的规律如下:
- 未知结点总能使贝叶斯球通过, 同时还反弹从其子结点方向来的贝叶斯球.
- 已知结点反弹从其父结点方向来的贝叶斯球, 截止从其子结点方向来的贝叶斯球.
这几条规则如下图所示.

图中用双线圈表示已知结点. 反映的规则从左至右依次是:
- 未知结点允许从其父结点方向来的贝叶斯球访问其任意子结点;
- 未知结点允许从其子结点方向来的贝叶斯球访问其任意父结点以及子结点;
- 已知结点允许从其父结点方向来的贝叶斯球访问其任意父结点;
- 已知结点截止从其子结点方向来的贝叶斯球.
还需加上边界条件, 即当前结点是图的边界点时:

注意两个反弹的情况, 前者是反弹到所有子结点, 后者是反弹到所有父结点.
下面看几个例子. 示意图中双线圈表示已知结点.
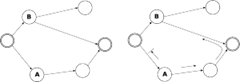
下图中, 设贝叶斯球从图中结点A出发, 右图给出了贝叶斯球的运动轨迹. 从图中看出, 只有左下角的那个结点与结点A条件独立.

下图中, 这个图中结点A与B非条件独立. 从A出发时, 尽管从左边的一条路径无法到达B, 但从右边的路径则是可以到达的.
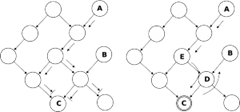
下图中, 左图表示 , 右图表示
, 右图表示 . 对于右图的结论也可以这样理解: 因为D的子结点C已知, 所以V形结构EDB中E与B非条件独立, 进而A与B非条件独立.
. 对于右图的结论也可以这样理解: 因为D的子结点C已知, 所以V形结构EDB中E与B非条件独立, 进而A与B非条件独立.
分享到:









 与
与 关于结点(或结点集合)
关于结点(或结点集合) 条件独立时我们称
条件独立时我们称 . D-Separation中的D指Directed. 从图形上看, 结点集合
. D-Separation中的D指Directed. 从图形上看, 结点集合 或
或 , 且
, 且 ;
; , 且
, 且 及其所有后代都不属于
及其所有后代都不属于
 ; 第三个图中,
; 第三个图中,  , 而
, 而 .
.





相关推荐
2. **朴素贝叶斯 (Naive Bayes)** 朴素贝叶斯分类器基于贝叶斯定理和特征条件独立假设。在Scikit-learn中,有多种朴素贝叶斯模型可供选择,如`GaussianNB`(高斯朴素贝叶斯)、`MultinomialNB`(多项式朴素贝叶斯...
3. **朴素贝叶斯**(Naive Bayes):适用于文本分类等场景。 - 创建模型:`from sklearn.naive_bayes import GaussianNB` - 初始化模型:`gnb = GaussianNB()` - 模型拟合:`gnb.fit(X_train, y_train)` 4. **K...
Tripple Farm:Match 3 Combination Game Complete Project 合成小镇三消Unity合成消除游戏项目游戏插件模版C# 支持Unity2020.3.4或更高 您知道像三合镇这样的著名益智游戏,并且您想制作一个自己的游戏。就是这样。这个包正好适合您。 这是一个完整的项目,您可以在零分钟内将其上传到 appstore 或 googleplay 商店。 基本规则: 3个或以上相同的道具可以匹配升级为新的道具。动物如果被困住,也可以合并。 羽毛: -移动(android/ios)就绪。 - 包含所有源代码。 -超过 12 座建筑/军团需要升级。 -三种特殊物品可以提供帮助。 - 三个不同的主题(场景和动物) -unity iap 支持 -Unity UI -广告位已准备好 -包含详细文档
内容概要:本文档是一份针对Java初学者的基础测试题,分为不定项选择题、简答题和编程题三大部分。选择题涵盖标识符、数组初始化、面向对象概念、运算符优先级、循环结构、对象行为、变量命名规则、基本
内容概要:本文详细介绍了如何利用MATLAB进行机器人运动学、动力学以及轨迹规划的建模与仿真。首先,通过具体的代码实例展示了正运动学和逆运动学的实现方法,包括使用DH参数建立机械臂模型、计算末端位姿以及求解关节角度。接着,讨论了雅克比矩阵的应用及其在速度控制中的重要性,并解释了如何检测和处理奇异位形。然后,深入探讨了动力学建模的方法,如使用拉格朗日方程和符号工具箱自动生成动力学方程。此外,还介绍了多种轨迹规划技术,包括抛物线插值和五次多项式插值,确保路径平滑性和可控性。最后,提供了常见仿真问题的解决方案,强调了在实际工程项目中需要注意的关键点。 适合人群:对机器人控制感兴趣的初学者、希望深入了解机器人运动学和动力学的学生及研究人员、从事机器人开发的技术人员。 使用场景及目标:① 学习如何使用MATLAB进行机器人运动学、动力学建模;② 掌握不同类型的轨迹规划方法及其应用场景;③ 解决仿真过程中遇到的各种问题,提高仿真的稳定性和准确性。 其他说明:文中提供的代码片段可以直接用于实验和教学,帮助读者更好地理解和掌握相关概念和技术。同时,针对实际应用中的挑战提出了实用的建议,有助于提升项目的成功率。
包括:源程序工程文件、Proteus仿真工程文件、配套技术手册等 1、采用51/52单片机作为主控芯片; 2、发送机:18B20测温、开关模拟灯光,发送数据; 3、接收机:接受数据、12864液晶显示;
内容概要:本文探讨了在微电网优化中如何处理风光能源的不确定性,特别是通过引入机会约束和概率序列的方法。首先介绍了风光能源的随机性和波动性带来的挑战,然后详细解释了机会约束的概念,即在一定概率水平下放松约束条件,从而提高模型灵活性。接着讨论了概率序列的应用,它通过对历史数据分析生成多个可能的风光发电场景及其概率,以此为基础构建优化模型的目标函数和约束条件。文中提供了具体的Matlab代码示例,演示了如何利用CPLEX求解器解决此类优化问题,并强调了参数选择、模型构建、约束添加以及求解过程中应注意的技术细节。此外,还提到了一些实用技巧,如通过调整MIP gap提升求解效率,使用K-means聚类减少场景数量以降低计算复杂度等。 适合人群:从事电力系统研究、微电网设计与运营的专业人士,尤其是那些对风光不确定性建模感兴趣的研究者和技术人员。 使用场景及目标:适用于需要评估和优化含有大量间歇性可再生能源接入的微电网系统,旨在提高系统的经济性和稳定性,确保在面对风光出力波动时仍能维持正常运作。 其他说明:文中提到的方法不仅有助于学术研究,也可应用于实际工程项目中,帮助工程师们制定更为稳健的微电网调度计划。同时,文中提供的代码片段可供读者参考并应用于类似的问题情境中。
linux之用户管理教程.md
内容概要:本文详细介绍了如何利用组态王和西门子S7-200 PLC构建六层或八层电梯控制系统。首先进行合理的IO地址分配,明确输入输出信号的功能及其对应的物理地址。接着深入解析了PLC源代码的关键部分,涵盖初始化、呼叫处理、电梯运行逻辑和平层处理等方面。此外,提供了组态王源代码用于实现动画仿真,展示了电梯轿厢的画面创建及动画连接方法。最后附上了详细的电气原理图和布局图,帮助理解和实施整个系统架构。 适合人群:从事工业自动化控制领域的工程师和技术人员,尤其是对PLC编程和人机界面开发感兴趣的从业者。 使用场景及目标:适用于教学培训、工程项目实践以及研究开发等场合。旨在为相关人员提供一个完整的电梯控制系统设计方案,便于他们掌握PLC编程技巧、熟悉组态软件的应用,并能够独立完成类似项目的开发。 其他说明:文中不仅包含了理论知识讲解,还分享了许多实际操作经验,如解决编码器丢脉冲的问题、优化平层停车精度的方法等。同时强调了安全性和可靠性方面的考虑,例如设置了多重保护机制以确保系统稳定运行。
在工业生产和设备运行过程中,滚动轴承故障、变压器油气故障等领域的数据分类与故障诊断至关重要。准确的数据分类与故障诊断能够及时发现设备潜在问题,避免故障恶化导致的生产事故与经济损失。LSTM能够捕获时序信息,马尔可夫场(MTF)能够一维信号转换为二维特征图,并结合CNN学习空间特征,MTF-1D-2D-CNN-LSTM-Attention模型通过将一维时序信号和二维图像融合,融合不同模态优势,并引入多头自注意力机制提高泛化能力,为数据分类与故障诊断提供了新的思路。实验结果表明,该模型在分类准确率、鲁棒性和泛化能力方面具有显著优势。多模态融合算法凭借其创新点和实验验证的有效性,在滚动轴承故障、变压器油气故障等领域展现出广阔的应用前景,有望推动相关领域故障诊断技术的进一步发展。 关键词:多模态融合;故障诊断;马尔可夫场;卷积神经网络;长短期记忆神经网络 适用平台:Matlab2023版本及以上。实验硬件设备配置如下:选用高性能计算机,搭载i7处理器,以确保数据处理和模型训练的高效性;配备16GB的内存,满足大规模数据加载和模型运算过程中的内存需求;使用高性能显卡,提供强大的并行计算能力,加速深度学习模型的训练过程。实验参数的选择依据多方面因素确定。
内容概要:本文档提供了一个面试模拟的指导框架,旨在为用户提供一个真实的面试体验。文档中的面试官名为Elian,被设定为性格温和冷静且思路清晰的形象,其主要职责是根据用户提供的简历信息和应聘岗位要求,进行一对一的模拟面试。面试官将逐一提出问题,确保每次只提一个问题,并等待候选人的回答结束后再继续下一个问题。面试官需要深入了解应聘岗位的具体要求,包括但不限于业务理解、行业知识、具体技能、专业背景以及项目经历等方面,从而全面评估候选人是否符合岗位需求。此外,文档强调了面试官应在用户主动发起提问后才开始回答,若用户未提供简历,面试官应首先邀请用户提供简历或描述应聘岗位; 适用人群:即将参加面试的求职者,特别是希望提前熟悉面试流程、提升面试技巧的人士; 使用场景及目标:①帮助求职者熟悉面试流程,提高应对实际面试的信心;②通过模拟面试,让求职者能够更好地展示自己的优势,发现自身不足之处并加以改进; 其他说明:此文档为文本格式,用户可以根据文档内容与面试官Elian进行互动,以达到最佳的模拟效果。在整个模拟过程中,用户应尽量真实地回答每一个问题,以便获得最贴近实际情况的反馈。
招聘技巧HR必看如何进行网络招聘和电话邀约.ppt
内容概要:本文详细介绍了利用三菱PLC(特别是FX系列)和组态王软件构建3x3书架式堆垛式立体库的方法。首先阐述了IO分配的原则,明确了输入输出信号的功能,如仓位检测、堆垛机运动控制等。接着深入解析了梯形图编程的具体实现,包括基本的左右移动控制、复杂的自动寻址逻辑,以及确保安全性的限位保护措施。还展示了接线图和原理图的作用,强调了正确的电气连接方式。最后讲解了组态王的画面设计技巧,通过图形化界面实现对立体库的操作和监控。 适用人群:从事自动化仓储系统设计、安装、调试的技术人员,尤其是熟悉三菱PLC和组态王的工程师。 使用场景及目标:适用于需要提高仓库空间利用率的小型仓储环境,旨在帮助技术人员掌握从硬件选型、电路设计到软件编程的全流程技能,最终实现高效稳定的自动化仓储管理。 其他说明:文中提供了多个实用的编程技巧和注意事项,如避免常见错误、优化性能参数等,有助于减少实际应用中的故障率并提升系统的可靠性。
内容概要:本文详细探讨了利用COMSOL进行电弧放电现象的模拟,重点在于采用磁流体方程(MHD)来耦合电磁、热流体和电路等多个物理场。文中介绍了关键的数学模型如磁流体动力学方程、热传导方程以及电路方程,并讨论了求解过程中遇到的技术难题,包括参数敏感性、求解器选择、网格划分等问题。此外,作者分享了许多实践经验,比如如何处理不同物理场之间的相互作用,怎样避免数值不稳定性和提高计算效率。 适用人群:适用于从事电弧放电研究的专业人士,尤其是那些希望通过数值模拟深入了解电弧行为并应用于实际工程项目的人群。 使用场景及目标:①帮助研究人员更好地理解和预测电弧放电过程中的各种物理现象;②为工程师提供优化电气设备设计的方法论支持;③指导使用者正确配置COMSOL软件的相关参数以确保高效稳定的仿真结果。 其他说明:尽管存在较高的计算复杂度和技术挑战,成功的电弧放电仿真能够显著提升对这一重要物理过程的认识水平,并促进相关领域的技术创新和发展。
内容概要:本文详细介绍了如何利用粒子群优化算法(PSO)改进极限学习机(KELM),以提升其在多维输入单维输出数据处理任务中的性能。首先简述了KELM的工作原理及其快速训练的特点,接着深入探讨了PSO算法的机制,包括粒子的速度和位置更新规则。然后展示了如何将PSO应用于优化KELM的关键参数,如输入权值和隐含层偏置,并提供了具体的Python代码实现。通过对模拟数据和实际数据集的实验对比,证明了PSO优化后的KELM在预测精度上有显著提升,尤其是在处理复杂数据时表现出色。 适合人群:对机器学习尤其是深度学习有一定了解的研究人员和技术爱好者,以及从事数据分析工作的专业人士。 使用场景及目标:适用于需要高效处理多维输入单维输出数据的任务,如时间序列预测、回归分析等。主要目标是通过优化模型参数,提高预测准确性并减少人工调参的时间成本。 其他说明:文中不仅给出了详细的理论解释,还附上了完整的代码示例,便于读者理解和实践。此外,还讨论了一些实用技巧,如参数选择、数据预处理等,有助于解决实际应用中的常见问题。
内容概要:本文介绍了利用粒子群算法(PSO)解决微网优化调度问题的方法。主要内容涵盖微网系统的组成(风力、光伏、储能、燃气轮机、柴油机)、需求响应机制、储能SOC约束处理及粒子群算法的具体实现。文中详细描述了目标函数的设计,包括发电成本、启停成本、需求响应惩罚项和SOC连续性惩罚项的计算方法。同时,阐述了粒子群算法的核心迭代逻辑及其参数调整策略,如惯性权重的线性递减策略。此外,还讨论了代码调试过程中遇到的问题及解决方案,并展示了仿真结果,证明了模型的有效性和优越性。 适合人群:从事电力系统优化、智能算法应用的研究人员和技术人员,特别是对微网调度感兴趣的读者。 使用场景及目标:适用于研究和开发微网优化调度系统,旨在提高供电稳定性的同时降低成本。具体应用场景包括但不限于分布式能源管理、工业园区能源调度等。目标是通过合理的调度策略,使微网系统在满足需求响应的前提下,实现经济效益最大化。 其他说明:本文提供的Matlab程序具有良好的模块化设计,便于扩展和维护。建议读者在理解和掌握基本原理的基础上,结合实际情况进行改进和创新。
KUKA机器人相关资料
基于多智能体的高层建筑分阶段火灾疏散仿 真及策略研究.pdf
Iterative Time Series Imputation by Maintaining Dependency Consistency (ACM TKDD 2024)
内容概要:本文详细探讨了带同步整流桥的交错PFC(功率因数校正)电路的设计与仿真实现。交错PFC通过多路PFC电路交错工作,降低了输入电流纹波,提高了功率密度。同步整流桥采用MOSFET代替传统二极管,减少了整流损耗,提升了效率。文中提供了关键代码片段,包括PWM控制、同步整流桥控制逻辑、电流环控制等,并介绍了如何在MATLAB/Simulink中搭建仿真模型,验证设计方案的有效性。此外,还讨论了仿真过程中遇到的问题及其解决方案,如死区时间处理、电流采样精度、负载突变应对等。 适合人群:从事电力电子设计的研究人员和技术工程师,尤其是对PFC技术和同步整流感兴趣的从业者。 使用场景及目标:适用于研究和开发高效的电源管理系统,旨在提高电能利用率,减少谐波污染,优化电源性能。目标是通过仿真实验验证设计方案的可行性,最终应用于实际硬件开发。 其他说明:文章强调了仿真与实际调试的区别,提醒读者在实际应用中需要注意的细节,如电流采样精度、死区时间和负载突变等问题。同时,提供了具体的代码实现和仿真技巧,帮助读者更好地理解和掌握这一复杂的技术。