一、中点画线算法:
//中点画线算法
void CMidPointLineView::MyMidLine(int x0, int y0, int x1, int y1)
{
CClientDC dc(this);
int a=0;
int b=0;
int d1=0;
int d2=0;
int d=0;
int x=0;
int y=0;
a=y0-y1;
b=x1-x0;
d=2*a+b;
d1=2*a;
d2=2*a+2*b;
x=x0;
y=y0;
dc.SetPixel(x,y,RGB(255,0,0));
while(x<x1)
{
if(d<0)
{
x++;
y++;
d += d2;
}
else
{
x++;
d += d1;
}
dc.SetPixel(x,y,RGB(255,0,0));
}
}
效果图如下:
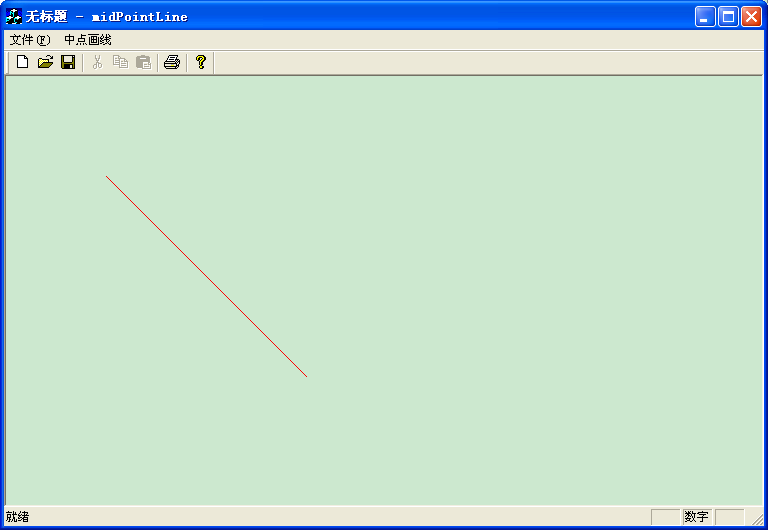
二、中点画圆算法:
//画1/8圆弧
void CMidPointCircleView::MyMidCircle(int x0,int y0, int r)
{
CClientDC dc(this);
int x=0;
int y=r;
float d=1.25-r;
CirclePoint(x0,y0,x,y);
while(x<=y)
{
if(d<0)
{
d+=2*x+3;
}
else
{
d+=2*(x-y)+5;
y--;
}
x++;
CirclePoint(x0,y0,x,y);
}
}
效果图如下:
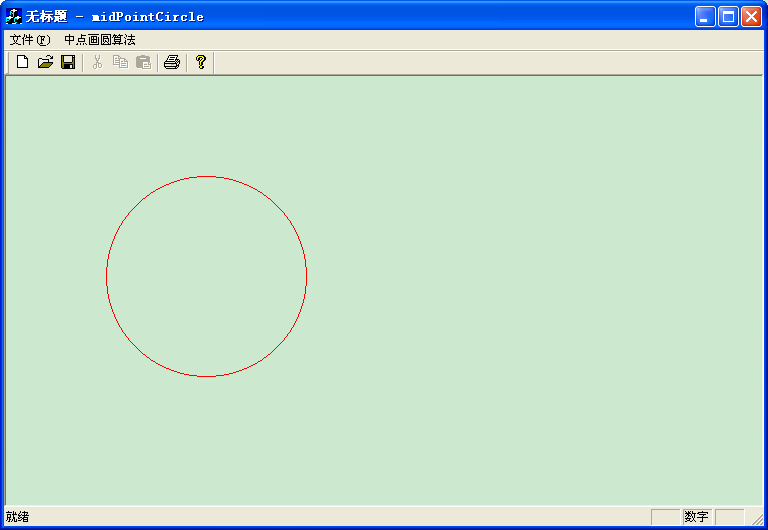
三、多边形裁剪算法:
//直线窗口裁剪
int CPolygonCutView::DrawLine(float x1, float y1, float x2, float y2)
{
CDC *pDC=GetDC();
int code1,code2,code;
float x,y;
CPen redpen(PS_SOLID,1,RGB(255,0,0));//创建画实线、线宽为2的红色画笔
CPen *old=pDC->SelectObject(&redpen);
encode(x1,y1,code1);
encode(x2,y2,code2);
while(code1!=0||code2!=0)
{
if(code1&code2)
return 1;//线段在窗口外,返回
code=code1;
if(code1==0)code=code2;
if(l&code)
{
x=left;
y=y1+(y2-y1)*(left-x1)/(x2-x1);
}
else if(r&code)
{
x=right;
y=y1+(y2-y1)*(right-x1)/(x2-x1);
}
else if(b&code)
{
y=bottom;
x=x1+(x2-x1)*(bottom-y1)/(y2-y1);
}
else if(t&code)
{
y=top;
x=x1+(x2-x1)*(top-y1)/(y2-y1);
}
if(code==code1)
{
x1=x;y1=y;encode(x,y,code1);
}
else
{
x2=x;y2=y;encode(x,y,code2);
}
}
pDC->MoveTo(x1,y1);
pDC->LineTo(x2,y2);
ReleaseDC(pDC);
return 1;
}
效果图如下:
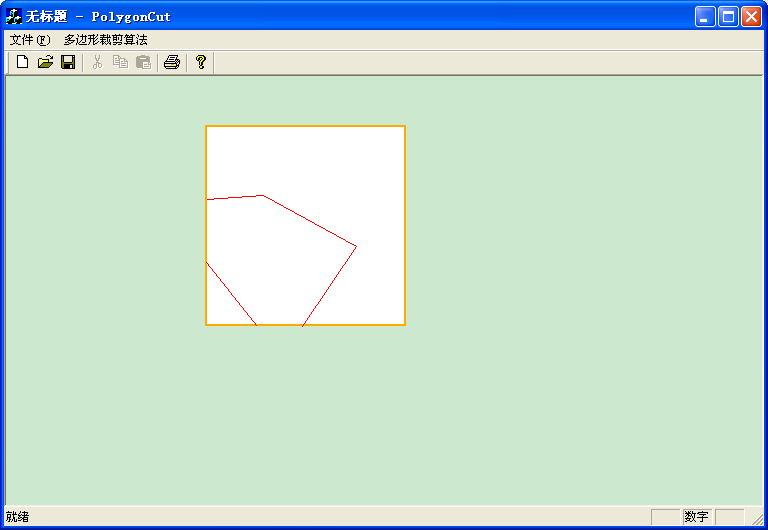
四、多边形区域填充算法:
//扫描线填充算法
void CFieldFillView::ScanlineSeedfill(CDC *pDC, int x, int y, COLORREF boundaryvalue, COLORREF newvalue)
{
int x0,xl,xr,y0,xid;
int flag,xnextspan;
stack<CPoint> s;//堆栈
CPoint p;
s.push(CPoint(x,y));//第一个种子入栈
while (!s.empty())//堆栈不为空
{
p = s.top();
s.pop();//取栈顶元素并弹栈
pDC->SetPixel(p.x,p.y,newvalue);//绘制像素点为指定颜色
x = p.x;y = p.y;
x0 =x + 1;
while (pDC->GetPixel(x0,y) != boundaryvalue)//填充右方元素
{
pDC->SetPixel(x0,y,newvalue);
x0++;
}
xr = x0 -1;//最右边像素
x0 = x -1;
while (pDC->GetPixel(x0,y) != boundaryvalue)//填充左方像素
{
pDC->SetPixel(x0,y,newvalue);
x0--;
}
xl = x0 + 1;//最左边像素
//检查上一条和下一条扫描线,若存在边界且未填充的像素
//则选取代表各连续区间的种子像素入栈
y0 = y;
for (int i=1;i>=-1;i-=2)
{
x0 = xr;
y = y0 + i;//获得上一行和下一行
while (x0 >= xl)
{
flag = 0;
while ((pDC->GetPixel(x0,y) != boundaryvalue)
&& (pDC->GetPixel(x0,y) != newvalue)
&& (x0 > xl))
{
if (flag == 0)
{
flag = 1;
xid = x0;
}
x0--;
}
if (flag == 1)
{
s.push(CPoint(xid,y));//新种子入栈
flag = 0;
}
xnextspan = x0;
while ((pDC->GetPixel(x0,y) == boundaryvalue)
|| (pDC->GetPixel(x0,y) == newvalue)
&& (x0 >= xl))
x0--;
if (xnextspan == x0) x0--;
}
}
}
}
效果图如下:
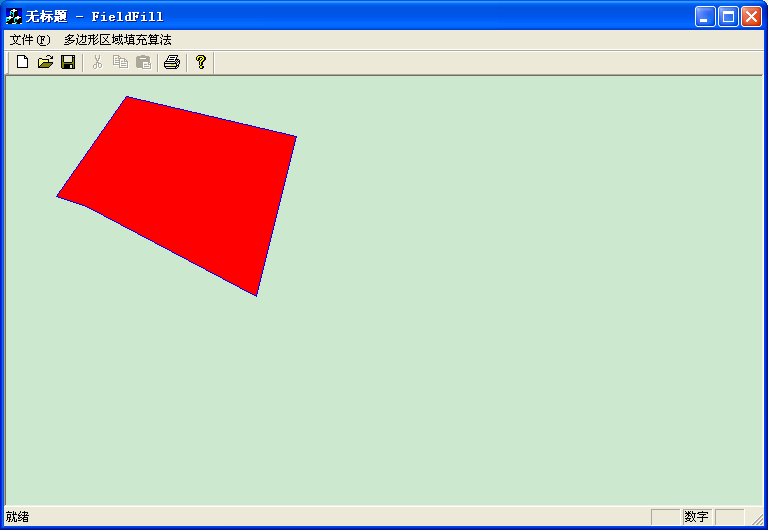
五、Bezier曲线生成算法:
//画Bezier曲线
void CBezierView::OnBezier()
{
CDC*pDC=GetDC();
RedrawWindow();
CPen redpen(PS_SOLID,2,RGB(255,0,0));//创建画笔
CPen *old=pDC->SelectObject(&redpen);
float x0=50,y0=80,x1=150,y1=250,x2=400,y2=130,x3=300,y3=70;
float x,y,dt,t,n=30.0;
int i ;
dt=1/n;
for(i=0;i<=n;i++)
{
t=i*dt;
x=x0*(1-t)*(1-t)*(1-t)+x1*3*t*(1-t)*(1-t)+x2*3*t*t*(1-t)+x3*t*t*t;
y=y0*(1-t)*(1-t)*(1-t)+y1*3*t*(1-t)*(1-t)+y2*3*t*t*(1-t)+y3*t*t*t;
if(i==0)pDC->MoveTo(x,y);
pDC->LineTo(x,y);
}
pDC->MoveTo(x0,y0);
pDC->LineTo(x1,y1);
pDC->LineTo(x2,y2);
pDC->LineTo(x3,y3);
pDC->SelectObject(old);
ReleaseDC(pDC);
}
效果图如下:
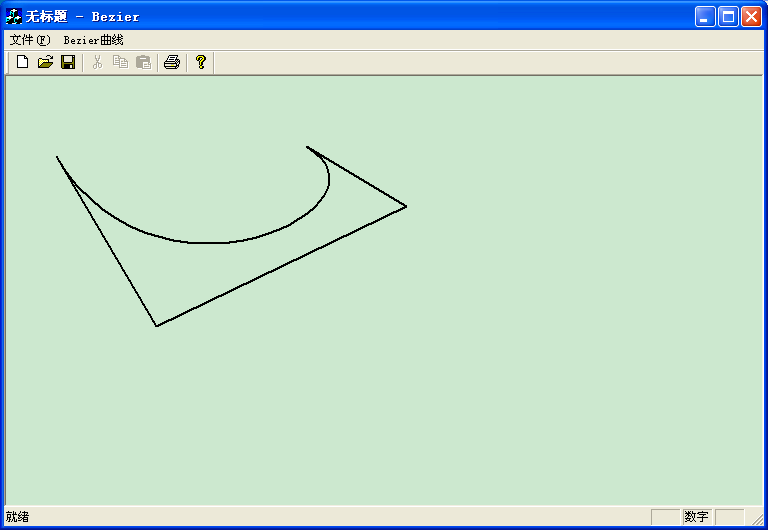
工程文件下载地址:http://www.kuaipan.cn/file/id_8128290032206914.htm
分享到:















相关推荐
在代码实现中,填充算法通常会包含以下几个关键部分: 1. 图形初始化:设置图形设备环境,如窗口大小、颜色模式等。 2. 用户交互:允许用户选择填充的起点或指定填充的区域。 3. 填充逻辑:根据选择的填充算法实现...
计算机图形学是一门涵盖广泛的学科,它涉及到计算机如何创建、处理和显示图像。在这个Java编写的教材中,我们深入探讨了几个关键的图形学算法及其实际应用。以下是这些算法的详细解析: 1. 直线扫描转换算法: ...
在学习和分析这个"graphics"源代码时,可以关注以下几个计算机图形学的重要知识点: 1. **图形绘制**:基础的直线、曲线、多边形等图形的生成算法,如Bresenham算法、DDA算法等。 2. **几何变换**:包括平移、旋转...
总结来说,这个压缩包提供了关于计算机图形学中基础图形变换和直线绘制算法的实现,涵盖了五角星与五边形的转换以及DDA和中点画线算法。对这些知识点的理解和掌握,是学习计算机图形学不可或缺的一部分,对于提升...
在计算机图形学中,多边形填充算法是一项基础且关键的技术,它用于将屏幕上或图像中的多边形区域填充成指定的颜色,为游戏、3D建模、GIS等应用提供支持。本文将深入探讨多边形填充算法的基本原理、常用方法以及C/C++...
在这些源代码案例中,你可能会遇到以下几个关键知识点: 1. **OpenGL**:这是一个跨语言、跨平台的编程接口,用于渲染2D、3D矢量图形。OpenGL提供了丰富的函数库,可以用来创建复杂的几何形状、控制渲染质量和实现...
计算机图形学演示程序是基于MFC(Microsoft Foundation Classes)框架和VC6.0(Visual C++ 6.0)开发的一个项目,旨在展示和实践计算机图形学的基本原理和算法。这个程序将理论与实践相结合,为学习者提供了一个直观...
计算机图形学主要涉及以下几个关键知识点: 1. **坐标系统与变换**:在图形学中,我们通常需要在不同的坐标系之间转换,如世界坐标、屏幕坐标和纹理坐标。变换包括平移、旋转、缩放和投影,这些都是通过矩阵运算来...
给定的压缩包文件包含了几个关键的计算机图形学概念的实现代码,接下来我们将详细探讨这些概念。 首先,"WordChar"可能是指文字字符的渲染。在计算机图形学中,文字通常被看作是图形元素,可以使用像素或向量图形...
通过"计算机图形学原理及算法教程(Visual C++版)第二版-1.pdf"这个文件,你可以深入学习和掌握这些关键概念,并且利用C++这种强大的编程语言来实现自己的图形应用程序。对于想要在游戏开发、图形设计或相关领域深造...
源代码可能会涵盖以下几个关键知识点: 1. **坐标系统**:理解笛卡尔坐标系、极坐标系和球面坐标系,以及它们在计算机图形中的应用。 2. **几何变换**:包括平移、旋转和缩放等,这些变换是图形学中的基础操作,用于...
实验指导书的核心内容围绕几个基础的图形绘制算法展开,这些算法是计算机图形学的基础,包括: 1. **DDA(数值微分)算法**:这是一种简单的直线绘制算法,通过连续的像素步进来逼近直线。它首先确定直线的起点和...
在阅读和学习这些示例代码时,有几个关键知识点是值得深入探讨的: 1. **基本图形绘制**:包括点、线和多边形的绘制。这些是最基本的元素,通过它们可以构建更复杂的图形。例如,Bresenham算法常用于高效地在屏幕上...
在计算机图形学中,关键的知识点包括以下几个方面: 1. **坐标系统**:计算机图形学中的图像通常在笛卡尔坐标系中表示,理解不同坐标系统(如世界坐标、相机坐标、屏幕坐标)之间的转换至关重要。 2. **几何建模**...
在这个“计算机图形学VC版+源代码”教程中,我们主要聚焦于使用Microsoft Visual C++(简称VC)这一编程环境来实现图形学的基本概念和技术。对于初学者来说,这是一个极好的起点,因为它提供了实际操作的机会,通过...
"裁剪算法"是计算机图形学中的关键组成部分,它用于确定图形对象哪些部分应该被显示,哪些部分应该被排除。 VC++(Visual C++)是一种广泛使用的编程环境,它提供了丰富的库函数和工具,使得开发者能够方便地实现...
计算机图形学是一门涵盖广泛的学科,它涉及到计算机如何创建、处理和显示图像。在本资源中,"计算机图形学——基于MFC三维图形开发 孔令德版",作者孔令德提供了一套针对MFC(Microsoft Foundation Classes)框架的...
总的来说,掌握多边形边缘填充算法是提升计算机图形学技能的关键一步,通过分析和实践孔令德的案例代码,可以深化对这些算法的理解,提高编程能力,并为未来在图形处理相关的项目中打下坚实的基础。
在这个"计算机图形学实验代码全集"中,我们将会深入探讨几个关键领域,这些领域都是计算机图形学的基础,也是游戏开发、虚拟现实、电影特效、工程设计等领域的核心技术。 首先,让我们从“图形相交—相切”开始。在...
在这个课程设计中,学生可能会接触到以下几个关键算法: 1. 直线绘制:Bresenham算法用于绘制像素级别的直线。 2. 多边形填充:扫描线算法用于填充二维多边形。 3. 三维图形:包括线框模型和表面模型的绘制,可能...