经典算法研究系列：一、A*搜索算法

经典算法研究系列：一、A*搜索算法

July 二零一一年一月

==============

博主说明：
1、此经典算法研究系列，此系列文章写的不够好之处，还望见谅。
2、本经典算法研究系列，系我参考资料，一篇一篇原创所作，转载必须注明作者本人July及出处。
3、本经典算法研究系列，精益求精，不断优化，永久更新，永久勘误。

欢迎，各位，与我一同学习探讨，交流研究。
有误之处，不吝指正。

-------------------------------------------

A* 搜寻算法

1968年，的一篇论文，“P. E. Hart, N. J. Nilsson, and B. Raphael. A formal basis for the heuristic determination of minimum cost paths in graphs. IEEE Trans. Syst. Sci. and Cybernetics, SSC-4(2):100-107, 1968”。从此，一种精巧、高效的算法------A*算法横空出世了，并在相关领域得到了广泛的应用。

DFS和BFS在展开子结点时均属于盲目型搜索，也就是说，它不会选择哪个结点在下一次搜索中更优而去跳转到该结点进行下一步的搜索。在运气不好的情形中，均需要试探完整个解集空间, 显然，只能适用于问题规模不大的搜索问题中。

那么，作为启发式算法中的A*算法，又比它们高效在哪里呢？

首先要来谈一下什么是启发式算法。

所谓启发式搜索，与DFS和BFS这类盲目型搜索最大的不同，就在于当前搜索结点往下选择下一步结点时，可以通过一个启发函数来进行选择，选择代价最少的结点作为下一步搜索结点而跳转其上（遇到有一个以上代价最少的结点，不妨选距离当前搜索点最近一次展开的搜索点进行下一步搜索）。

一个经过仔细设计的启发函数，往往在很快的时间内就可得到一个搜索问题的最优解，
对于NP问题，亦可在多项式时间内得到一个较优解。

是的，关键就是如何设计这个启发函数。

A*算法，作为启发式算法中很重要的一种，被广泛应用在最优路径求解和一些策略设计的问题中。
而A*算法最为核心的部分，就在于它的一个估值函数的设计上：

f(n)=g(n)+h(n)

其中f(n)是每个可能试探点的估值，它有两部分组成：
一部分，为g(n)，它表示从起始搜索点到当前点的代价（通常用某结点在搜索树中的深度来表示）。
另一部分，即h(n)，它表示启发式搜索中最为重要的一部分，即当前结点到目标结点的估值，

h(n)设计的好坏，直接影响着具有此种启发式函数的启发式算法的是否能称为A*算法。

一种具有f(n)=g(n)+h(n)策略的启发式算法能成为A*算法的充分条件是：

1、搜索树上存在着从起始点到终了点的最优路径。
2、问题域是有限的。
3、所有结点的子结点的搜索代价值>0。
4、h(n)=<h*(n) （h*(n)为实际问题的代价值）。

当此四个条件都满足时，一个具有f(n)=g(n)+h(n)策略的启发式算法能成为A*算法，并一定能找到最优解。

对于一个搜索问题，显然，条件1,2,3都是很容易满足的，而条件4： h(n)<=h*(n)是需要精心设计的，由于h*(n)显然是无法知道的，所以，一个满足条件4的启发策略h(n)就来的难能可贵了。

不过，对于图的最优路径搜索和八数码问题，有些相关策略h(n)不仅很好理解，而且已经在理论上证明是满足条件4的，从而为这个算法的推广起到了决定性的作用。

且h(n)距离h*(n)的呈度不能过大，否则h(n)就没有过强的区分能力，算法效率并不会很高。对一个好的h(n)的评价是：h(n)在h*(n)的下界之下，并且尽量接近h*(n).

维基百科对本A*搜索算法的解释：

A*搜寻算法，俗称A星算法。这是一种在图形平面上，有多个节点的路径，求出最低通过成本的算法。

常用于游戏中的NPC的移动计算，或线上游戏的BOT的移动计算上。
该算法像Dijkstra算法一样，可以找到一条最短路径；也像BFS一样，进行启发式的搜索。

在此算法中，
g(n)表示从起点到任意顶点n的实际距离，
h(n)表示任意顶点n到目标顶点的估算距离。
//即，起点-->任意顶点g(n)-->目标顶点h(n)

因此，A*算法的公式为：
f(n)=g(n)+h(n)。

这个公式遵循以下特性：
I、如果h(n)为0，只需求出g(n)，即求出起点到任意顶点n的最短路径，
则转化为单源最短路径问题，即Dijkstra算法。
II、如果h(n)<=n到目标的实际距离，则一定可以求出最优解。而且h(n)越小，需要计算的节点越多，算法效率越低。

A*搜寻算法的算法实现：

A*是求这样一个和最短路径有关的问题，那单纯的最短路径问题当然可以用A*来算，对于g(n)就是[S,n]，在搜索过程中计算，而h(n)我想不出很好的办法，对于一个抽象的图搜索，很难找到很好的h(n)，因为h(n)和具体的问题有关。只好是h(n)=0，退为有序搜索，举一个小小的例子：

V0->V1，V2，V3，V4，V5的路径之和。即好比一个人从V0点出发，要达到V1..V5，五个点。图中达到过的点，可以作为到达其它点的连通桥。

下面的问题，即是求此起始顶点V0->途径任意顶点V1、V2、V3、V4->目标顶点V5的最短路径。

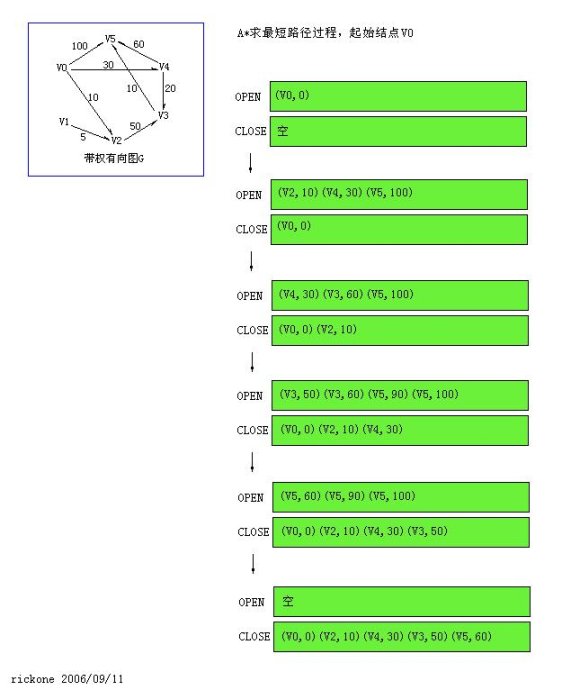
//是的，图片是引用rickone 的。

通过上图，我们可以看出：
A*算法最为核心的过程，就在每次选择下一个当前搜索点时，是从所有已探知的但未搜索过点中(可能是不同层，亦可不在同一条支路上)，选取f值最小的结点进行展开。
而所有“已探知的但未搜索过点”可以通过一个按f值升序的队列(即优先队列)进行排列。
这样，在整体的搜索过程中，只要按照类似广度优先的算法框架，从优先队列中弹出队首元素（f值），对其可能子结点计算g、h和f值，直到优先队列为空(无解)或找到终止点为止。

A*算法与广度优先和深度优先的联系就在于，当g(n)=0时，该算法类似于DFS，当h(n)=0时，该算法类似于BFS , 这一点，可以通过上面的A*搜索树的具体过程中将h(n)设为0或将g(n)设为0而得到。

A*算法流程：

首先将起始结点S放入OPEN表，CLOSE表置空，算法开始时：
1、如果OPEN表不为空，从表头取一个结点n，如果为空算法失败。
2、n是目标解吗？是，找到一个解（继续寻找，或终止算法）。

3、将n的所有后继结点展开，就是从n可以直接关联的结点（子结点），如果不在CLOSE表中，就将它们放入OPEN表，并把S放入CLOSE表，同时计算每一个后继结点的估价值f(n)，将OPEN表按f(x)排序，最小的放在表头，重复算法，回到1。

//OPEN-->CLOSE，起点-->任意顶点g(n)-->目标顶点h(n)

closedset := the empty set //已经被估算的节点集合
openset := set containing the initial node //将要被估算的节点集合
g_score[start] := 0 //g(n)
h_score[start] := heuristic_estimate_of_distance(start, goal) //h(n)
f_score[start] := h_score[start]

while openset is not empty //若OPEN表不为空
x := the node in openset having the lowest f_score[] value //x为OPEN表中最小的
if x = goal //如果x是一个解
return reconstruct_path(came_from,goal) //
remove x from openset
add x to closedset//x放入CLSOE表

for each y in neighbor_nodes(x)
if y in closedset
continue
tentative_g_score := g_score[x] + dist_between(x,y)

if y not in openset
add y to openset
tentative_is_better := true
else if tentative_g_score < g_score[y]
tentative_is_better := true
else
tentative_is_better := false
if tentative_is_better = true
came_from[y] := x
g_score[y] := tentative_g_score
h_score[y] := heuristic_estimate_of_distance(y, goal) //x-->y-->goal
f_score[y] := g_score[y] + h_score[y]
return failure

function reconstruct_path(came_from,current_node)
if came_from[current_node] is set
p = reconstruct_path(came_from,came_from[current_node])
return (p + current_node)
else
return the empty path

与结点写在一起的数值表示那个结点的价值f(n)，当OPEN表为空时CLOSE表中将求得从V0到其它所有结点的最短路径。

考虑到算法性能，外循环中每次从OPEN表取一个元素，共取了n次（共n个结点），每次展开一个结点的后续结点时，需O(n)次，同时再对OPEN表做一次排序，OPEN表大小是O(n)量级的，若用快排就是O(nlogn)，乘以外循环总的复杂度是O(n^2 * logn)，

如果每次不是对OPEN表进行排序，因为总是不断地有新的结点添加进来，所以不用进行排序，而是每次从OPEN表中求一个最小的，那只需要O(n)的复杂度，所以总的复杂度为O(n*n)，这相当于Dijkstra算法。

在这个算法基础之上稍加改进就是Dijkstra算法。OPEN表中常出现这样的表项：(Vk,fk1)(Vk,fk2)(Vk,fk3)，而从算法上看，只有fk最小的一个才有用，于是可以将它们合并，整个OPEN表表示当前的从V0到其它各点的最短路径，定长为n，且初始时为V0可直接到达的权值（不能到达为INFINITY），于是就成了Dijkstra算法。

本文完。
July、二零一一年二月十日更新。

------------------------------------------------
后续：July、二零一一年三月一日更新。
简述A*最短路径算法的方法：
目标：从当前位置A到目标位置B找到一条最短的行走路径。

方法：从A点开始，遍历所有的可走路径，记录到一个结构中，记录内容为（位置点，最小步数）
当任何第二次走到一个点的时候，判断最小步骤是否小于记录的内容，如果是，则更新掉原最小步数，一直到所有的路径点都不能继续都了为止，最终那个点被标注的最小步数既是最短路径，
而反向找跟它相连的步数相继少一个值的点连起来就形成了最短路径，当多个点相同，则任意取一条即可。

总结：
A*算法实际是个穷举算法，也与课本上教的最短路径算法类似。课本上教的是两头往中间走，也是所有路径都走一次，每一个点标注最短值。

作者声明:

本人July对本博客所有任何内容和资料享有版权，转载请注明作者本人July及出处。

永远，向您的厚道致敬。谢谢。July、二零一零年十二月二十三日。