一步一图一代码,一定要让你真正彻底明白红黑树
作者:July二零一一年一月九日
<!--EndFragment-->
-----------------------------
本文参考:
I、 The Art of Computer Programming Volume I
II、 Introduction to Algorithms, Second Edition
III、The Annotated STL Sources
IV、 Wikipedia
V、 Algorithms In C Third Edition
VI、 本人写的关于红黑树的前三篇文章:
第一篇:教你透彻了解红黑树:
http://blog.csdn.net/v_JULY_v/archive/2010/12/29/6105630.aspx
第二篇:红黑树算法的层层剖析与逐步实现
http://blog.csdn.net/v_JULY_v/archive/2010/12/31/6109153.aspx
第三篇:教你彻底实现红黑树:红黑树的c源码实现与剖析
http://blog.csdn.net/v_JULY_v/archive/2011/01/03/6114226.aspx
---------------------------------------------
前言:
1、有读者反应,说看了我的前几篇文章,对红黑树的了解还是不够透彻。
2、我个人觉得,如果我一步一步,用图+代码来阐述各种插入、删除情况,可能会更直观易懂。
3、既然写了红黑树,那么我就一定要把它真正写好,让读者真正彻底明白红黑树。
本文相对我前面红黑树相关的3篇文章,主要有以下几点改进:
1.图、文字叙述、代码编写,彼此对应,明朗而清晰。
2.宏观总结,红黑树的性质与插入、删除情况的认识。
3.代码来的更直接,结合图,给你最直观的感受,彻底明白红黑树。
ok,首先,以下几点,你现在应该是要清楚明白了的:
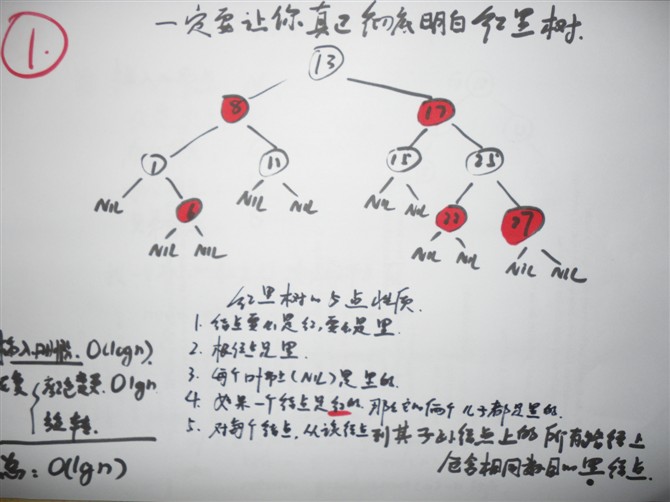
I、红黑树的五个性质:
1)每个结点要么是红的,要么是黑的。
2)根结点是黑的。
3)每个叶结点,即空结点(NIL)是黑的。
4)如果一个结点是红的,那么它的俩个儿子都是黑的。
5)对每个结点,从该结点到其子孙结点的所有路径上包含相同数目的黑结点。
II、红黑树插入的几种情况:
情况1,z的叔叔y是红色的。
情况2:z的叔叔y是黑色的,且z是右孩子
情况3:z的叔叔y是黑色的,且z是左孩子
III、红黑树删除的几种情况。
情况1:x的兄弟w是红色的。
情况2:x的兄弟w是黑色的,且w的俩个孩子都是黑色的。
情况3:x的兄弟w是黑色的,且w的左孩子是红色,w的右孩子是黑色。
情况4:x的兄弟w是黑色的,且w的右孩子是红色的。
除此之外,还得明确一点:
IV、我们知道,红黑树插入、或删除结点后,
可能会违背、或破坏红黑树的原有的性质,
所以为了使插入、或删除结点后的树依然维持为一棵新的红黑树,
那就要做俩方面的工作:
1、部分结点颜色,重新着色
2、调整部分指针的指向,即左旋、右旋。
V、并区别以下俩种操作:
1)红黑树插入、删除结点的操作,RB-INSERT(T, z),RB-DELETE(T, z)
2).红黑树已经插入、删除结点之后,
为了保持红黑树原有的红黑性质而做的恢复与保持红黑性质的操作。
如RB-INSERT-FIXUP(T, z),RB-DELETE-FIXUP(T, x)
以上这5点,我已经在我前面的2篇文章,都已阐述过不少次了,希望,你现在已经透彻明了。
---------------------------------------------------------------------
本文,着重图解分析红黑树插入、删除结点后为了维持红黑性质而做修复工作的各种情况。
[下文各种插入、删除的情况,与我的第二篇文章,红黑树算法的实现与剖析相对应]
ok,开始。
一、在下面的分析中,我们约定:
要插入的节点为,N
父亲节点,P
祖父节点,G
叔叔节点,U
兄弟节点,S
如下图所示,找一个节点的祖父和叔叔节点:
node grandparent(node n) //祖父
{
return n->parent->parent;
}
node uncle(node n) //叔叔
{
if (n->parent == grandparent(n)->left)
return grandparent(n)->right;
else
return grandparent(n)->left;
}

二、红黑树插入的几种情况
情形1: 新节点N位于树的根上,没有父节点
void insert_case1(node n) {
if (n->parent == NULL)
n->color = BLACK;
else
insert_case2(n);
}
情形2: 新节点的父节点P是黑色
void insert_case2(node n) {
if (n->parent->color == BLACK)
return; /* 树仍旧有效 */
else
insert_case3(n);
}

情形3:父节点P、叔叔节点U,都为红色,
[对应第二篇文章中,的情况1:z的叔叔是红色的。]
void insert_case3(node n) {
if (uncle(n) != NULL && uncle(n)->color == RED) {
n->parent->color = BLACK;
uncle(n)->color = BLACK;
grandparent(n)->color = RED;
insert_case1(grandparent(n)); //因为祖父节点可能是红色的,违反性质4,递归情形1.
}
else
insert_case4(n); //否则,叔叔是黑色的,转到下述情形4处理。

此时新插入节点N做为P的左子节点或右子节点都属于上述情形3,上图仅显示N做为P左子的情形。
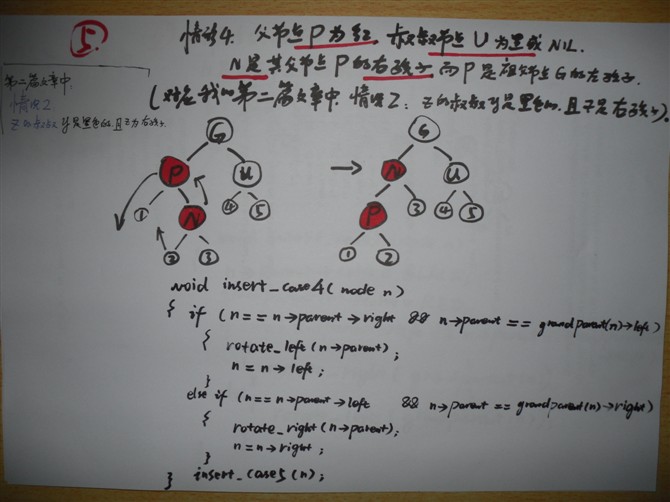
情形4: 父节点P是红色,叔叔节点U是黑色或NIL;
插入节点N是其父节点P的右孩子,而父节点P又是其父节点的左孩子。
[对应我第二篇文章中,的情况2:z的叔叔是黑色的,且z是右孩子]
void insert_case4(node n) {
if (n == n->parent->right && n->parent == grandparent(n)->left) {
rotate_left(n->parent);
n = n->left;
} else if (n == n->parent->left && n->parent == grandparent(n)->right) {
rotate_right(n->parent);
n = n->right;
}
insert_case5(n); //转到下述情形5处理。
情形5: 父节点P是红色,而叔父节点U 是黑色或NIL,
要插入的节点N 是其父节点的左孩子,而父节点P又是其父G的左孩子。
[对应我第二篇文章中,情况3:z的叔叔是黑色的,且z是左孩子。]
void insert_case5(node n) {
n->parent->color = BLACK;
grandparent(n)->color = RED;
if (n == n->parent->left && n->parent == grandparent(n)->left) {
rotate_right(grandparent(n));
} else {
/* 反情况,N 是其父节点的右孩子,而父节点P又是其父G的右孩子 */
rotate_left(grandparent(n));
}
}

三、红黑树删除的几种情况
上文我们约定,兄弟节点设为S,我们使用下述函数找到兄弟节点:
struct node * sibling(struct node *n) //找兄弟节点
{
if (n == n->parent->left)
return n->parent->right;
else
return n->parent->left;
}
情况1: N 是新的根。
void
delete_case1(struct node *n)
{
if (n->parent != NULL)
delete_case2(n);
}

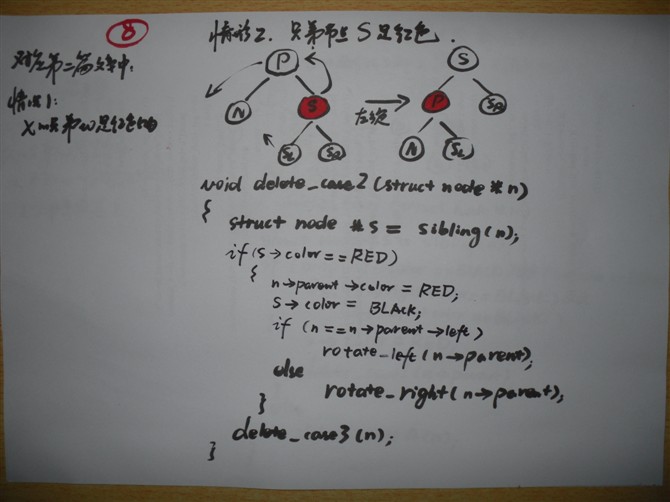
情形2:兄弟节点S是红色
[对应我第二篇文章中,情况1:x的兄弟w是红色的。]
void delete_case2(struct node *n)
{
struct node *s = sibling(n);
if (s->color == RED) {
n->parent->color = RED;
s->color = BLACK;
if (n == n->parent->left)
rotate_left(n->parent); //左旋
else
rotate_right(n->parent);
}
delete_case3(n);
}
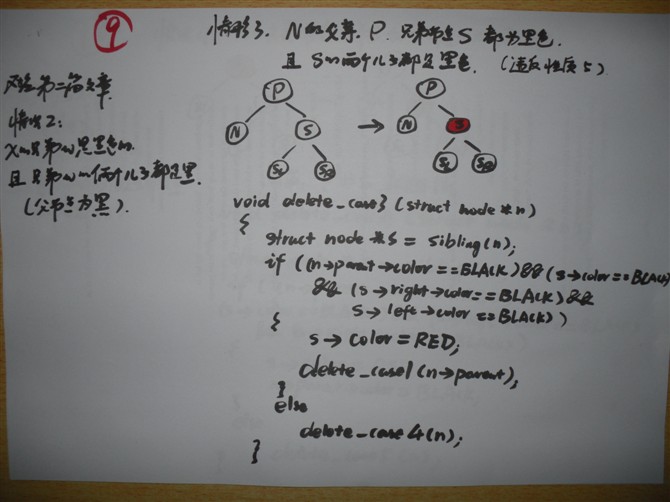
情况 3: 兄弟节点S是黑色的,且S的俩个儿子都是黑色的。但N的父节点P,是黑色。
[对应我第二篇文章中,情况2:x的兄弟w是黑色的,且兄弟w的俩个儿子都是黑色的。
(这里,父节点P为黑)]
void delete_case3(struct node *n)
{
struct node *s = sibling(n);
if ((n->parent->color == BLACK) &&
(s->color == BLACK) &&
(s->left->color == BLACK) &&
(s->right->color == BLACK)) {
s->color = RED;
delete_case1(n->parent);
} else
delete_case4(n);
}
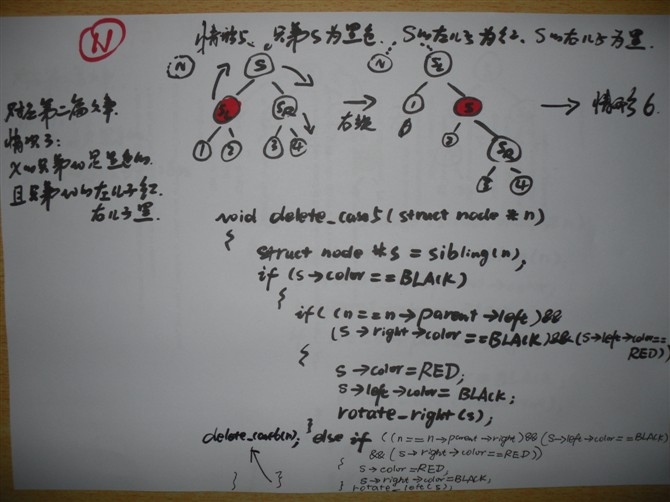
情况4: 兄弟节点S 是黑色的、S 的儿子也都是黑色的,但是 N 的父亲P,是红色。
[还是对应我第二篇文章中,情况2:x的兄弟w是黑色的,且w的俩个孩子都是黑色的。
(这里,父节点P为红)]
void delete_case4(struct node *n)
{
struct node *s = sibling(n);
if ((n->parent->color == RED) &&
(s->color == BLACK) &&
(s->left->color == BLACK) &&
(s->right->color == BLACK)) {
s->color = RED;
n->parent->color = BLACK;
} else
delete_case5(n);
}
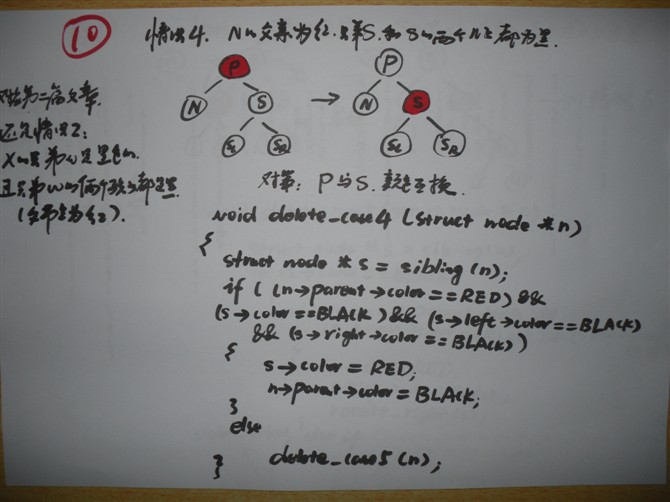
情况5: 兄弟S为黑色,S 的左儿子是红色,S 的右儿子是黑色,而N是它父亲的左儿子。
//此种情况,最后转化到下面的情况6。
[对应我第二篇文章中,情况3:x的兄弟w是黑色的,w的左孩子是红色,w的右孩子是黑色。]
void delete_case5(struct node *n)
{
struct node *s = sibling(n);
if (s->color == BLACK)
if ((n == n->parent->left) &&
(s->right->color == BLACK) &&
(s->left->color == RED)) {
// this last test is trivial too due to cases 2-4.
s->color = RED;
s->left->color = BLACK;
rotate_right(s);
} else if ((n == n->parent->right) &&
(s->left->color == BLACK) &&
(s->right->color == RED)) {
// this last test is trivial too due to cases 2-4.
s->color = RED;
s->right->color = BLACK;
rotate_left(s);
}
}
delete_case6(n); //转到情况6。
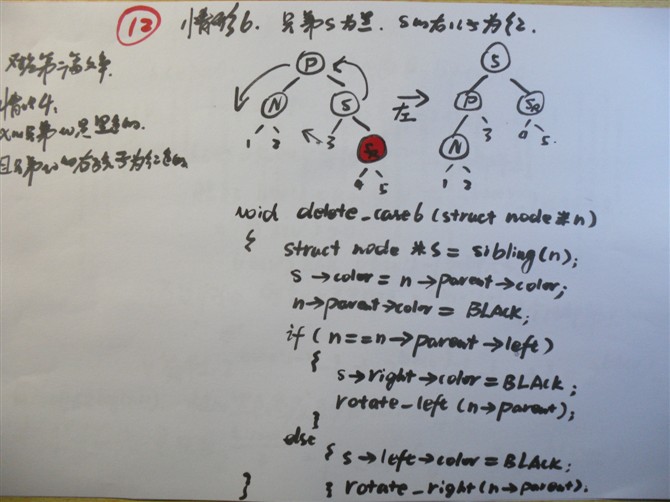
情况6: 兄弟节点S是黑色,S的右儿子是红色,而 N 是它父亲的左儿子。
[对应我第二篇文章中,情况4:x的兄弟w是黑色的,且w的右孩子时红色的。]
void delete_case6(struct node *n)
{
struct node *s = sibling(n);
s->color = n->parent->color;
n->parent->color = BLACK;
if (n == n->parent->left) {
s->right->color = BLACK;
rotate_left(n->parent);
} else {
s->left->color = BLACK;
rotate_right(n->parent);
}
}
//呵呵,画这12张图,直接从中午画到了晚上。希望,此文能让你明白。
四、红黑树的插入、删除情况时间复杂度的分析
因为每一个红黑树也是一个特化的二叉查找树,
因此红黑树上的只读操作与普通二叉查找树上的只读操作相同。
然而,在红黑树上进行插入操作和删除操作会导致不再符合红黑树的性质。
恢复红黑树的属性需要少量(O(log n))的颜色变更(实际是非常快速的)和
不超过三次树旋转(对于插入操作是两次)。
虽然插入和删除很复杂,但操作时间仍可以保持为 O(log n) 次。

ok,完。
后记:
此红黑树系列,前前后后,已经写了4篇文章,如果读者读完了这4篇文章,
对红黑树有一个相对之前来说,比较透彻的理解,
那么,也不枉费,我花这么多篇幅、花好几个钟头去画红黑树了。
真正理解一个数据结构、算法,最紧要的还是真正待用、实践的时候体会。
欢迎,各位,将现在、或以后学习、工作中运用此红黑树结构、算法的经验与我分享。
谢谢。:D。
----------------------------------------
作者声明:
本人July对本博客所有文章和资料享有版权,转载、或引用任何内容请注明出处。
向您的厚道致敬。谢谢。二零一一年一月九日。
分享到:























相关推荐
红黑树是一种自平衡的二叉查找树,它能确保任何一条路径的长度都不会超过其他路径的两倍。红黑树的每个节点都包含五个域:Key、parent、left、right、color,其中Key是节点的关键字,parent、left和right分别为指向...
红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树红黑树...
手把手实现红黑树,一步一步彻底实现红黑树,面试不再愁。...
"红黑树的代码实现" 红黑树是一种自平衡的二叉查找树,它具有良好的查找、插入和删除性能。红黑树的代码实现是使用C++语言编写的,使用模板实现,可以对任意类型的数据进行处理。 红黑树的节点结构体定义为: ```...
红黑树是一种自平衡二叉查找树,由Rudolf Bayer在1972年提出。它的设计目标是在保持二叉查找树特性的同时,通过特定的规则维持树的平衡,从而保证了插入、删除和查找操作的时间复杂度都能达到O(log n)。在这个“红黑...
总结来说,这篇博客和提供的Java代码旨在介绍如何在Java中实现红黑树这一数据结构。通过理解和实现红黑树,开发者可以更好地掌握高级数据结构及其在实际问题中的应用,这对于提升编程能力和优化算法效率至关重要。
在"红黑树代码实现及分析"这个主题中,你可以找到关于红黑树的具体实现细节,包括如何初始化树、插入和删除节点的步骤,以及如何进行颜色翻转和旋转等操作。通过分析这些代码,你可以更好地理解红黑树的工作原理,并...
根据给定的信息,本文将详细解释红黑树的C语言实现方法,...总之,这段代码提供了一个完整的红黑树的C语言实现框架,通过理解和掌握这些核心概念和实现细节,可以帮助开发者更好地理解和应用红黑树这一高效的数据结构。
红黑树是一种自平衡二叉查找树,由Rudolf Bayer在1972年提出。它的设计目标是在保持查询效率的同时,通过特定的规则保证插入和删除操作能在较短时间内完成,以解决AVL树在频繁插入和删除时可能会遇到的过度平衡问题...
红黑树,全称为“红色-黑色树”,是一种在计算机科学中广泛应用的自平衡二叉查找树(BST),由Rudolf Bayer于1972年提出。这种数据结构的独特之处在于它通过颜色属性(红色或黑色)来维护树的平衡,确保在最坏情况下...
通过阅读代码,你可以学习如何在实际编程中应用红黑树的平衡策略,这对于理解和优化数据结构和算法的性能至关重要。同时,这也有助于提升对二叉树和自平衡树概念的理解,这些都是计算机科学和软件工程领域的重要基础...
红黑树(Red-Black Tree)是一种自平衡二叉查找树,由计算机科学家鲁道夫·贝尔在1978年提出。它在保持二叉查找树特性的同时,通过引入颜色属性来确保树的平衡,从而提高了数据操作的效率。红黑树的主要目标是保证在...
红黑树是一种自平衡二叉查找树,由Rudolf Bayer在1972年提出。它的设计目标是在保持二叉查找树基本属性的同时,通过引入颜色(红色或黑色)来确保树的平衡,从而在插入和删除操作后能够快速恢复平衡状态,减少最坏...
红黑树是一种自平衡二叉查找树,它的设计目的是为了在保持查找效率的同时,通过特定的规则维护树的平衡,从而使得插入、删除和查找操作的时间复杂度保持在O(log n)。红黑树的特性使得它在各种数据结构如关联数组、...
红黑树(Red-Black Tree)是一种自平衡二叉查找树,它在计算机科学中扮演着重要的角色,尤其是在实现高效的数据结构和算法时。在Java中,虽然标准库并未直接提供红黑树的类,但我们可以自定义实现,如提供的`Red...
### 红黑树实现代码解析 #### 一、引言 红黑树是一种自平衡二叉查找树,它的每个节点都包含一个颜色属性(红色或黑色)。在操作过程中,通过对树进行一定的调整来保持其平衡特性,从而保证了树的高度始终保持在对数...
红黑树是一种自平衡二叉查找树,由Rudolf Bayer在1972年提出。它的设计目标是在保持搜索效率的同时,通过特定的颜色规则来维护树的平衡,从而保证了插入、删除和查找操作的时间复杂度都能达到O(log n)。在本项目中,...
3. 测试代码:这部分可能演示了如何使用这些数据结构,如何创建和操作链表和红黑树,以及如何将它们编译为库以便在其他项目中复用。 学习这部分内容有助于深入理解Linux内核的工作原理,特别是涉及到内存管理和文件...
红黑树的添加、删除、遍历等代码&以及注释,提供测试样例~!