经典算法研究系列:八、再谈启发式搜索算法
作者:July 二零一一年二月十日
本文参考:
I、 维基百科、
II、 人工智能-09 启发式搜索、
III、本BLOG内,经典算法研究系列:一、A*搜索算法
----------------------------
引言:
A*搜索算法,作为经典算法研究系列的开篇文章,之前已在本BLOG内有所阐述。
但要真正理解A*搜索算法,还是得先从启发式搜索算法谈起。
毕竟,A*搜索算法也是启发式算法中的一种。ok,切入正题。
一、何谓启发式搜索
启发式搜索算法有点像广度优先搜索,不同的是,它会优先顺着有启发性和具有特定信息的节点搜索下去
,这些节点可能是到达目标的最好路径。
我们称这个过程为最优(best-first)或启发式搜索。
下面是其基本思想:
1) 假定有一个启发式(评估)函数ˆf ,可以帮助确定下一个要扩展的最优节点,
我们采用一个约定,即ˆf的值小表示找到了好的节点。
这个函数基于指定问题域的信息,它是状态描述的一个实数值函数。
2) 下一个要扩展的节点n是ˆf(n)值最小的节点(假定节点扩展产生一个节点的所有后
继)。
3) 当下一个要扩展的节点是目标节点时过程终止。
我们常常可以为最优搜索指定好的评估函数。
如在8数码问题中,可以用不正确位置的数字个数作为状态描述好坏的一个度量:
f(n) = 位置不正确的数字个数(和目标相比)
在搜索过程中采用这个启发式函数将产生图9 - 1所示的图,每个节点的数值是该节点的
值。
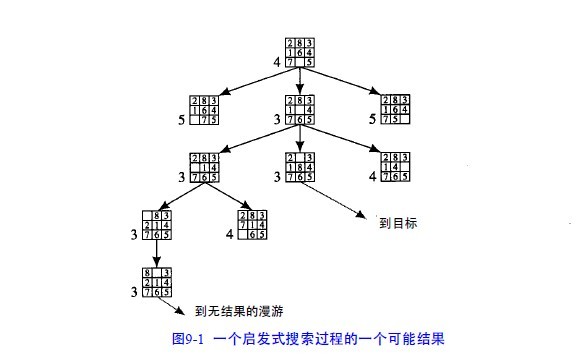
图9-1 一个启发式搜索过程的一个可能结果
上述例子表明,在搜索过程中我们需要偏向有利于回溯到早期路径的搜索(为了避免由于过分的优化试探
而陷入“花园小径”)。
因此我们加了一个“深度因子”给ˆf: ˆf(n)= gˆ(n)+ hˆ(n) ,gˆ(n)是对图中节点n的“深度”估计(即
从开始节点到n的最短路径长度),hˆ(n)是对节点n的启发或评估。
像前面一样,如果gˆ(n)= 搜索图中节点n的深度,hˆ(n)=不正确位置的数字个数(和目标相比), 我们可以得到图9-2。
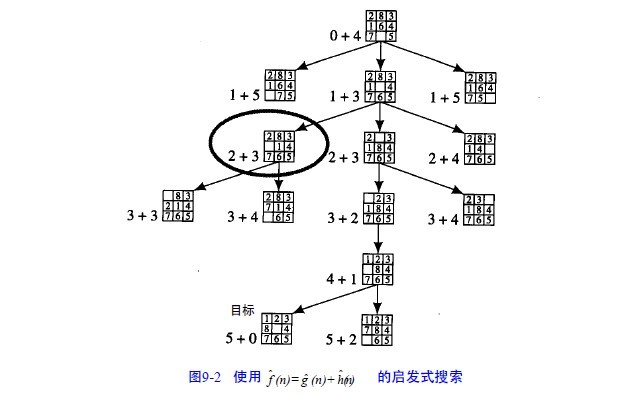
在这个图中,把gˆ(n)和hˆ(n)的值写在每个节点的旁边,在这种情况下,可以看到搜索相当直接地朝着目
标进行(除了用圆圈标注的节点外)。
这些例子提出了两个重要的问题。
第一,我们如何为最优搜索决定评估函数?
第二,最优搜索的特性是什么?它能找到到达目标节点的好路径吗?
本文主要讨论最优搜索的形式表示。作为例子,下面介绍一个包括最优搜索版本的一般图搜索算法
(为了更详细地了解启发式搜索,可以参考引用的文章和Pearl写的书[pearl 1984])。
二、一个通用的图搜索算法
为了更准确地解释启发式搜索过程,这里提出一个通用的图搜索算法,它允许各种
用户—偏爱启发式的或盲目的,进行定制。我把这个算法叫做图搜索(GRAPHSEARCH)。
下面是(第一个版本)它的定义。
GRAPHSEACH:
1) 生成一个仅包含开始节点n0的搜索树Tr。把n0放在一个称为OPEN的有序列表中。
2) 生成一个初始值为空的列表CLOSED。
3) 如果OPEN为空,则失败并退出。
4) 选出OPEN中的第一个节点,并将它从OPEN中移出,放入CLOSED中。称该节点为n。
5) 如果n是目标节点,顺着Tr中的弧从n回溯到n0找到一条路径,获得解决方案,则成功退
出(弧在第6步产生)。
6) 扩展节点n,生成n的后继节点集M。通过在Tr中建立从n到M中每个成员的弧生成n的后继。
7) 按照任意的模式或启发式方式对列表OPEN重新排序。
8) 返回步骤3 。
这个算法可用来执行最优搜索、广度优先搜索或深度优先搜索。
在广度优先搜索中,新节点只要放在OPEN的尾部即可(先进先出, FIFO),节点不用重排。
在深度优先搜索中,新节点放在OPEN的开始(后进先出,LIFO)。
在最优(也叫启发式)搜索中,按照节点的启发式方式来重排OPEN。
三、略谈A*搜索算法
用最优搜索算法详细说明GRAPHSEARCH。
最优搜索算法根据函数的增加值,(在上述第7步)重排OPEN中的节
点,如8数码问题。把GRAPHSEACH的这种算法称为算法A*。
下面将会看到,定义使A*执行广度搜索或相同代价搜索的函数是可行的。为了确定要用的函数族,必须先
介绍一些其他符号。
设g(n) = 从开始节点n0到节点n的一个最小代价路径的代价。
设h(n) =节点n和目标节点(遍及所有可能的目标节点以及从n到它们的所有可能路径)之间的最小代价路径的实际代价。
那么f(n) = g(n) + h(n)就是从n0到目标节点并且经过节点n的最小代价路径的代价。
注意f(n0)= h(n0)是从n0到目标节点的一个(不受限的)最小代价路径的代价。
对每个节点n,设gˆ(n)(深度因子)是由A*发现的到节点n的最小代价路径的代价,hˆ(n)(启发因子)是h(n)的某个估计。
在算法A*中,我们用ˆf(n)= gˆ(n)+ hˆ(n)。
注意,如果算法A*中的恒等于0,就成为相同代价搜索。这些定义示例在图3中。

算法A*:
1)生成一个只包含开始节点n0的搜索图G,把n0放在一个叫OPEN的列表上。
2)生成一个列表CLOSED,它的初始值为空。
3)如果OPEN为空,则失败退出。
4)选择OPEN上的第一个节点,把它从OPEN中移入CLOSED,称该节点为n。
5)如果n是目标节点,顺着G中,从n到n0的指针找到一条路径,获得解决方案,成功退出
(该指针定义了一个搜索树,在第7步建立)。
6)扩展节点n,生成其后继节点集M,在G中,n的祖先不能在M中。在G中安置M的成
员,使它们成为n的后继。
7) 从M的每一个不在G中的成员建立一个指向n的指针(例如,既不在OPEN中,也不在
CLOSED中)。把M的这些成员加到OPEN中。对的每一个已在OPEN 中或CLOSED
中的成员m,如果到目前为止找到的到达m的最好路径通过n,就把它的指针指向n。对
已在CLOSE中的M的每一个成员,重定向它在G中的每一个后继,以使它们顺着到目前
为止发现的最好路径指向它们的祖先。
8) 按递增值,重排OPEN(相同最小值可根据搜索树中的最深节点来解决)。
9) 返回第3步。
在第7步中,如果搜索过程发现一条路径到达一个节点的代价比现存的路径代价低,
我们就要重定向指向该节点的指针。已经在CLOSED中的节点子孙的重定向保存了后面
的搜索结果,但是可能需要指数级的计算代价。因此,第7步常常不会实现。随着搜索
的向前推进,其中有些指针最终将会被重定向。
更多,可参考:经典算法研究系列:一、A*搜索算法:
http://blog.csdn.net/v_JULY_v/archive/2010/12/23/6093380.aspx
四、启发式算法相关问题
4.1、启发式算法与最短路径问题
启发式通常用于资讯充份的搜寻算法,例如最好优先贪婪算
法与A*。
最好优先贪婪算法会为启发式函数选择最低代价的节点;
A*则会为g(n) + h(n)选择最低代价的节点,此g(n)是从起始节点到目前节点的路径的确实代价。
如果h(n)是可接受的(admissible)意即h(n)未曾付出超过达到目标的代价,则A*一定会找出最佳解。
最能感受到启发式算法好处的经典问题是n-puzzle。此问题在计算错误的拼图图形,与计算任两块拼图的曼哈顿距离的总和以及它距离目的有多远时,使用了本算法。注意,上述两条件都必须在可接受的范围内。
曼哈顿距离是一个简单版本的n-puzzle问题,因为我们假设可以独立移动一个方块到我们想要的位置,而暂不考虑会移到其他方块的问题。
给我们一群合理的启发式函式h1(n),h2(n),...,hi(n),而函式h(n) = max{h1(n),h2(n),...,hi(n)}则是
个可预测这些函式的启发式函式。
一个在1993年由A.E. Prieditis写出的程式ABSOLVER就运用了这些技术,这程式可以自动为问题产生启发
式算法。ABSOLVER为8-puzzle产生的启发式算法优于任何先前存在的!而且它也发现了第一个有用的解魔
术方块的启发式程式。
4.2、启发式算法对运算效能的影响
任何的搜寻问题中,每个节点都有b个选择以及到达目标的深度d,一个毫无技巧的算法通常都要搜寻bd个
节点才能找到答案。
启发式算法借由使用某种切割机制降低了分叉率(branching factor)以改进搜寻效率,由b降到较低的b'。分叉率可以用来定义启发式算法的偏序关系,例如:若在一个n节点的搜寻树上,
h1(n)的分叉率较h2(n)低,则 h1(n) < h2(n)。
启发式为每个要解决特定问题的搜寻树的每个节点提供了较低的分叉率,因此它们拥有较佳效率的计算能力。
完。
分享到:













相关推荐
超启发式算法和传统启发式算法的主要区别在于,超启发式算法提供了一种高层次启发式方法,通过管理或操纵一系列低层次启发式算法,以产生新的启发式算法,而传统启发式算法则是一种基于直观或经验构造的算法。...
本书《生产排程之启发式算法》由Bassem Jarboui、Patrick Siarry和Jacques Teghem共同编辑,首次出版于2013年,旨在介绍一系列用于解决生产排程问题的元启发式算法。这些算法包括但不限于遗传算法、模拟退火算法、...
### 传播式启发式图搜索算法PRA及PRA #### 概述 本文提出了一种新的传播式启发式图搜索算法——PRA(Propagational Heuristic Graph Search Algorithm),该算法基于传播值的概念,旨在优化传统启发式图搜索算法RA...
通过结合元启发式算法和禁忌搜索算法,研究者提出了一种新的解决方案。 #### 二、元启发式算法简介 元启发式算法是一种用于解决复杂优化问题的高级算法框架。这类算法的特点在于它们不寻求精确解,而是通过近似方法...
在压缩包文件“第21章”中,很可能包含了关于启发式算法优化的具体案例、实现方法和进一步的研究,可能涵盖了一些经典的优化技术,如动态规划、贪心策略、回溯法等。这些内容对于深入理解和应用启发式算法的优化具有...
### 现代启发式算法理论研究 #### 引言 近年来,一类基于生物学、物理学以及人工智能技术的现代启发式算法得到了快速发展。这类算法具备全局优化能力、强鲁棒性、高通用性,并且适用于并行处理。由于其高效的优化...
本文是对十三个经典算法的研究与总结,旨在帮助读者理解和掌握这些重要的算法。这些算法涵盖了不同的领域,包括路径搜索、最短路径、动态规划、图遍历、数据结构、字符串匹配、遗传算法、搜索策略、图像处理、傅里叶...
在深入探讨“高级排产计划(Advanced Planning and Scheduling,简称APS)中启发式算法的研究与实现”这一主题之前,我们首先需要理解APS系统的基本概念及其在现代制造业中的重要性。APS是一种高度复杂的生产调度...
【标题】:“a*启发式搜索算法的matlab仿真程序” 在计算机科学中,路径搜索问题是一个常见的挑战,尤其是在游戏、机器人导航和图形学等领域。a*(读作"a-star")启发式搜索算法是一种非常有效的解决这类问题的方法...
在人工智能领域,八数码问题(又称滑动拼图游戏)是一个经典的示例,用于教授和研究各种搜索算法,包括启发式优先搜索。本项目重点在于使用C++编程语言实现启发式优先算法,这是一种高效的求解策略,特别是对于解决...
在这样的背景下,启发式算法作为一种有效的解决工具,被提出并应用于单件生产排产问题中。启发式算法是指在解决优化问题时,通过近似解或合理的方法来找到问题的满意解的算法。这些算法通常在解决问题的过程中不断...
cpp-Ghostman项目是一个专为C++开发者设计的搜索算法演示平台,它主要聚焦于两种重要的搜索策略:盲搜索(也称无信息搜索)和启发式搜索。这两种算法在解决各种复杂问题,特别是在游戏AI、路径规划以及问题求解等...
在自动采摘机器人路径规划研究中,启发式搜索算法能够帮助机器人更高效地在环境内进行移动,减少不必要的探索,从而节省时间,提升作业效率。 A*算法是启发式搜索算法中的一种,它结合了Dijkstra算法和最佳优先搜索...
### 启发式算法之大规模邻域搜索技术详解 #### 引言 在解决实际的最优化问题时,经常会遇到计算复杂度极高的情况。针对这类问题,传统的精确求解方法往往难以在合理的时间内找到最优解。因此,启发式算法成为了一种...
通过研究和理解这些Matlab代码,可以深入学习RSA的工作原理,了解如何将其应用于实际问题的求解,同时也可以为其他自然启发式优化算法的学习提供参考。此外,对Matlab编程技巧的提升以及优化算法的理解,对于在科研...
### 动态规划启发式算法求解时变车辆调度问题 #### 一、问题背景及研究意义 在交通网络中,车辆的行驶时间不仅受到节点间距离的影响,还受到多种时变因素(如交通流量、交通管制、天气状况等)的影响。这种特性...
国内外学者对最短路径算法的研究已经非常深入,包括经典的Dijkstra算法和一系列启发式算法,如A*、Bellman-Ford、Floyd-Warshall等。Dijkstra算法虽然保证找到最短路径,但其时间复杂度较高,不适用于大型网络。启发...
基于电商配送中心人到货整箱拣选系统,考虑拣选器具和商品包装体积,构造以最大化里程节约量为目标的订单分批模型,提出基于启发式拣选路径下节约里程的订单分批算法,并结合某企业物流中心订单数据对该算法进行仿真...
根据给定文件的信息,我们可以提炼出以下关于“十五个经典算法研究与总结”的知识点: ### 一、A*搜索算法 - **定义**:A*(A星)搜索算法是一种结合了最佳优先搜索和广度优先搜索优点的启发式搜索算法,它能够...