x = (x1,...,xn) 和y = (y1,...,yn) 之间的距离为
(1)欧氏距离 EuclideanDistanceMeasure

(2)曼哈顿距离 ManhattanDistanceMeasure
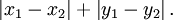
(3)马氏距离MahalanobisDistanceMeasure
马氏距离是由印度统计学家马哈拉诺比斯提出的,表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似 度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的)并且是尺度无关的 (scale-invariant),即独立于测量尺度。 对于一个均值为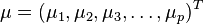 ,协方差矩阵为
,协方差矩阵为 的多变量向量
的多变量向量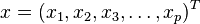 ,其马氏距离为
,其马氏距离为

马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为 的随机变量
的随机变量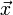 与
与 的差异程度:
的差异程度:

如果协方差矩阵为单位矩阵,马氏距离就简化为欧氏距离;如果协方差矩阵为对角阵,其也可称为正规化的欧氏距离。

其中 是
是 的标准差。
的标准差。
(4)余弦距离 CosineDistanceMeasure
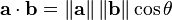
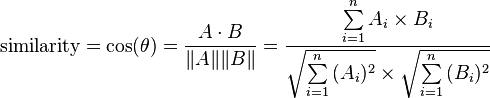
(5)汉明距离
在信息论中,两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。换句话说,它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。 例如:
1011101 与1001001 之间的汉明距离是 2。
2143896 与2233796 之间的汉明距离是 3。
"toned" 与 "roses" 之间的汉明距离是 3。
(6)平方欧几里德距离度量 SquaredEuclideanDistanceMeasure

(7)Tanimoto距离 TanimotoDistanceMeasure

(8)加权距离度量 WeightedDistanceMeasure ,具体实现有:WeightedEuclideanDistanceMeasure和WeightedManhattanDistanceMeasure
用欧几里德距离和曼哈顿距离实现。加权距离度量是Mahout的高级特征,它能让你在不同维上赋予不同的权重,以此对距离度量信息产生影 响,WeightedDistanceMeasure在向量格式化中需要序列化为文件。变量对距离的影响是不一样的,通过权值来确定。
(9)切比雪夫距离 ChebyshevDistanceMeasure
若二点p及q的直角坐标系坐标为 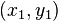 及
及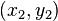 ,则切比雪夫距离为
,则切比雪夫距离为
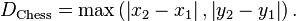






相关推荐
这个压缩包包含的是Mahout项目不同版本的核心库,分别是mahout-core-0.9.jar、mahout-core-0.8.jar和mahout-core-0.1.jar。这些版本的差异在于功能的完善、性能的优化以及对新特性的支持。 1. **Mahout核心功能**:...
"mahout-distribution-0.9.tar.gz"是Apache Mahout的0.9版本的发行包,包含了完整的源代码、文档和所需的依赖库。 **一、Mahout的背景与目标** Apache Mahout项目始于2008年,旨在简化大规模机器学习过程,提供可...
在"apache-mahout-distribution-0.11.0-src.zip"这个压缩包中,您将找到Mahout 0.11.0版本的源代码,这对于开发者和研究者来说是一个宝贵的资源,他们可以深入理解算法的内部工作原理,进行定制化开发或优化。...
mahout-0.9-cdh5.5.0.tar.gz
《Apache Maven与Mahout实战:基于maven_mahout_template-mahout-0.8的探索》 Apache Maven是一款强大的项目管理和依赖管理工具,广泛应用于Java开发领域。它通过一个项目对象模型(Project Object Model,POM)来...
mahout-core-0.9.jar,支持版本hadoop-2.2.x,由mahout-distribution-0.9.tar.gz源码构建生成jar包。
mahout-integration-0.7mahout-integration-0.7mahout-integration-0.7mahout-integration-0.7
mahout-distribution-0.5-src.zip mahout 源码包
标题中的"mahout-distribution-0.9-src.zip"指的是Mahout项目在0.9版本的源代码分布,这对于开发者来说是一个宝贵的资源,可以深入理解其内部实现并进行定制化开发。 Apache Mahout的核心特性主要体现在以下几个...
mahout-examples-0.10.1-job.jar 已经包含分词程序,替换掉mahout默认的jar包
mahout-distribution-0.10.0-src.tar.gz
mahout中需要用到的一个版本jar包:mahout-core-0.3.jar
这个压缩包“mahout-distribution-0.12.2-src.tar.gz”是Mahout项目的一个源码版本,版本号为0.12.2,提供给开发者进行深度研究和定制化开发。在解压后的文件“apache-mahout-distribution-0.12.2”中,我们可以找到...
重新编译mahout-examples-0.9-job.jar,增加分类指标:最小最大精度、召回率。详情见http://blog.csdn.net/u012948976/article/details/50203249
apache-mahout-distribution-0.12.1.tar.gz 开源版本 .
例如,可以通过修改或添加新的距离度量方法来优化聚类效果,或者调整推荐算法的参数以提升推荐准确率。 总结,Apache Mahout 0.7是机器学习领域的重要资源,其源码提供了深入理解算法实现的机会。通过研究源码,...
在Mahout-distribution-0.8-src这个源代码包中,我们可以深入理解其内部机制,同时也为开发者提供了实现自定义机器学习模型的可能。 一、Mahout 0.8概览 Mahout 0.8 版本是该项目的一个重要里程碑,它包含了丰富的...
"mahout-distribution-0.9含jar包" 是一个包含了Mahout项目0.9版本的预编译二进制文件集合,其中不包含源代码,适合那些希望直接使用Mahout功能而不需要进行编译或开发的用户。 在Mahout 0.9版本中,你可以找到以下...
在Mahout Taste Webapp工程中,需要添加对mahout-examples的依赖,这一步骤是必须的,因为示例代码提供了实际运行推荐系统所必需的组件。 6. 配置推荐引擎的属性 在Mahout Taste Webapp的recommender.properties...
mahout-math-0.8.jar mahout-math-0.8.jar