堆排序及其分析

摘自http://www.cnblogs.com/zabery/archive/2011/07/26/2117103.html

前言

记得在学习数据结构的时候一味的想用代码实现算法，重视的是写出来的代码有一个正确的输入，然后有一个正确的输出，那么就很满足了。从网上看了许多 的代码，看了之后貌似懂了，自己写完之后也正确了，但是不久之后就忘了，因为大脑在回忆的时候，只依稀记得代码中的部分，那么的模糊，根本不能再次写出正 确的代码，也许在第一次写的时候是因为参考了别人的代码，看过之后大脑可以进行短暂的高清晰记忆，于是欺骗了我，以为自己写出来的，满足了成就感。可是代 码是计算机识别的，而我们更喜欢文字，图像。所以我们在学习算法的时候要注重算法的原理以及算法的分析，用文字，图像表达出来，然后当需要用的时候再将文 字转换为代码。记忆分为三个步骤：编码，存储和检索，就以学习为例，先理解知识，再归纳知识，最后巩固知识，为了以后的应用而方便检索知识。

堆排序过程

堆分为大根堆和小根堆，是完全二叉树。大根堆的要求是每个节点的值都不大于其父节点的值，即A[PARENT[i]] >= A[i]。在数组的非降序排序中，需要使用的就是大根堆，因为根据大根堆的要求可知，最大的值一定在堆顶。

既然是堆排序，自然需要先建立一个堆，而建堆的核心内容是调整堆，使二叉树满足堆的定义（每个节点的值都不大于其父节点的值）。调堆的过程应该从最后一个非叶子节点开 始，假设有数组A = {1, 3, 4, 5, 7, 2, 6, 8, 0}。那么调堆的过程如下图，数组下标从0开始，A[3] = 5开始。分别与左孩子和右孩子比较大小，如果A[3]最大，则不用调整，否则和孩子中的值最大的一个交换位置，在图1中是A[7] > A[3] > A[8]，所以A[3]与A[7]对换，从图1.1转到图1.2。

所以建堆的过程就是

   1: for ( i = headLen/2; i >= 0; i++)

   2:  

   3:        do AdjustHeap(A, heapLen, i)

调堆：如果初始数组是非降序排序，那么就不需要调堆，直接就满足堆的定义，此为最好情况，运行时间为Θ(1)；如果初始数组是如图1.5，只有 A[0] = 1不满足堆的定义，经过与子节点的比较调整到图1.6，但是图1.6仍然不满足堆的定义，所以要递归调整，一直到满足堆的定义或者到堆底为止。如果递归调 堆到堆底才结束，那么是最坏情况，运行时间为O(h) (h为需要调整的节点的高度，堆底高度为0，堆顶高度为floor(logn) )。

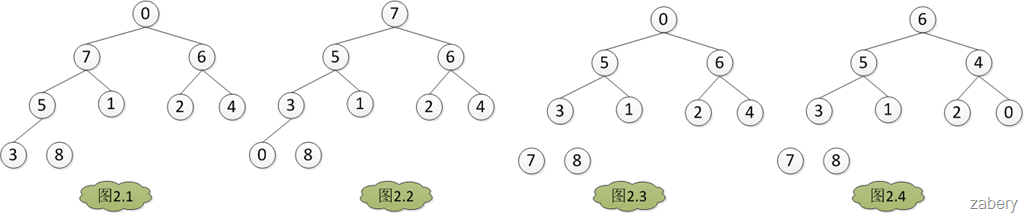
建堆完成之后，堆如图1.7是个大根堆。将A[0] = 8 与 A[heapLen-1]交换,然后heapLen减一，如图2.1，然后AdjustHeap(A, heapLen-1, 0)，如图2.2。如此交换堆的第一个元

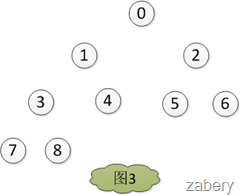
素和堆的最后一个元素，然后堆的大小heapLen减一，对堆的大小为heapLen的堆进行调堆，如此循环，直到heapLen == 1时停止，最后得出结果如图3。

   1: /*

   2:     输入：数组A，堆的长度hLen，以及需要调整的节点i

   3:     功能：调堆

   4: */

   5:  

   6: void AdjustHeap(int A[], int hLen, int i)

   7: {

   8:     int left = LeftChild(i);  //节点i的左孩子

   9:     int right = RightChild(i); //节点i的右孩子节点

  10:     int largest = i;

  11:     int temp;

  12:  

  13:     while(left < hLen || right < hLen)

  14:     {

  15:         if (left < hLen && A[largest] < A[left])

  16:         {

  17:             largest = left;

  18:         }

  19:         

  20:         if (right < hLen && A[largest] < A[right])

  21:         {

  22:             largest = right;

  23:         }

  24:  

  25:         if (i != largest)   //如果最大值不是父节点

  26:         {

  27:              temp = A[largest]; //交换父节点和和拥有最大值的子节点交换

  28:              A[largest] = A[i];

  29:              A[i] = temp;

  30:  

  31:             i = largest;         //新的父节点，以备迭代调堆

  32:             left = LeftChild(i);  //新的子节点

  33:             right = RightChild(i);

  34:         }

  35:         else

  36:         {

  37:             break;

  38:         }

  39:     }

  40: }

  41:  

  42: /*

  43:     输入：数组A，堆的大小hLen

  44:     功能：建堆

  45: */

  46: void BuildHeap(int A[], int hLen)

  47: {

  48:     int i;

  49:     int begin = hLen/2 - 1;  //最后一个非叶子节点

  50:     for (i = begin; i >= 0; i--)

  51:     {

  52:         AdjustHeap(A, hLen, i);  

  53:     }

  54: }

  55:  

  56: /*

  57:     输入：数组A，待排序数组的大小aLen

  58:     功能：堆排序

  59: */

  60: void HeapSort(int A[], int aLen)

  61: {

  62:     int hLen = aLen;

  63:     int temp;

  64:  

  65:     BuildHeap(A, hLen);      //建堆

  66:  

  67:     while (hLen > 1)

  68:     {

  69:         temp = A[hLen-1];    //交换堆的第一个元素和堆的最后一个元素

  70:         A[hLen-1] = A[0];

  71:         A[0] = temp;

  72:         hLen--;        //堆的大小减一

  73:         AdjustHeap(A, hLen, 0);  //调堆

  74:     }

  75: }

性能分析

• 调堆：上面已经分析了，调堆的运行时间为O(h)。
• 建堆：每一层最多的节点个数为n1 = ceil(n/(2^(h+1))),

因此，建堆的运行时间是O(n)。

• 循环调堆（代码67-74），因为需要调堆的是堆顶元素，所以运行时间是O(h) = O(floor(logn))。所以循环调堆的运行时间为O(nlogn)。

总运行时间T(n) = O(nlogn) + O(n) = O(nlogn)。对于堆排序的最好情况与最坏情况的运行时间，因为最坏与最好的输入都只是影响建堆的运行时间O(1)或者O(n)，而在总体时间中占重 要比例的是循环调堆的过程，即O(nlogn) + O(1) =O(nlogn) + O(n) = O(nlogn)。因此最好或者最坏情况下，堆排序的运行时间都是O(nlogn)。而且堆排序还是原地算法（in-place algorithm）。

 

 

从上述过程可知，堆排序其实也是一种选择排序，是一种树形选择排序。只不过直接选择排序中，为了从R[1...n]中选择最大记录，需比较n-1次，然后 从R[1...n-2]中选择最大记录需比较n-2次。事实上这n-2次比较中有很多已经在前面的n-1次比较中已经做过，而树形选择排序恰好利用树形的 特点保存了部分前面的比较结果，因此可以减少比较次数。对于n个关键字序列，最坏情况下每个节点需比较log2(n)次，因此其最坏情况下时间复杂度为 nlogn。堆排序为不稳定排序，不适合记录较少的排序。

 

 

参考http://www.cnblogs.com/dolphin0520/archive/2011/10/06/2199741.html